2024年中考数学二轮复习突破课件:专题三 多解问题(共57张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习突破课件:专题三 多解问题(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:38:33 | ||
图片预览


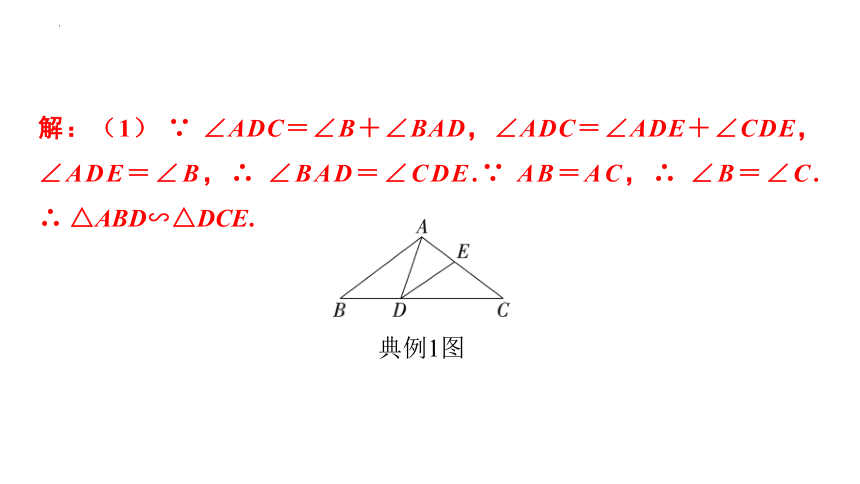





文档简介
(共57张PPT)
专题三 多解问题
类型1 特殊三角形中的多解题
考向1:与等腰三角形相关的分类讨论
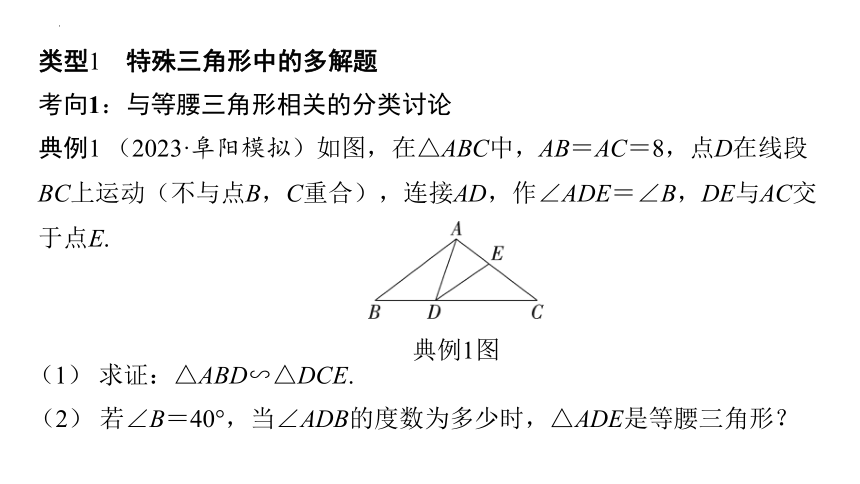
典例1 (2023·阜阳模拟)如图,在△ABC中,AB=AC=8,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=∠B,DE与AC交于点E.
典例1图
(1) 求证:△ABD∽△DCE.
(2) 若∠B=40°,当∠ADB的度数为多少时,△ADE是等腰三角形?
[思路点拨] (1) 根据三角形外角的性质证明∠BAD=∠CDE,再根据等腰三角形的性质证明∠B=∠C,即可证明△ABD∽△DCE.(2) 分三种情况:DA=DE;AD=AE;EA=ED.根据等腰三角形的性质分别求出∠ADB的度数即可.
解:(1) ∵ ∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠ADE=∠B,∴ ∠BAD=∠CDE.∵ AB=AC,∴ ∠B=∠C.
∴ △ABD∽△DCE.
典例1图
(2) 当DA=DE时,∠DEA=∠DAE.∵ ∠ADE=∠B=∠C=40°,
∴ ∠DAE=∠DEA=×(180°-40°)=70°.∴ ∠ADB=∠DAE+∠C=110°.当AD=AE时,∠DEA=∠ADE=∠B=40°=∠C.此时点D与点B重合,不合题意.当EA=ED时,∠EAD=∠ADE=∠B=40°.∴ ∠ADB=∠EAD+∠C=80°.综上所述,当∠ADB的度数为110°或80°时,△ADE是等腰三角形.
典例1图
跟踪训练
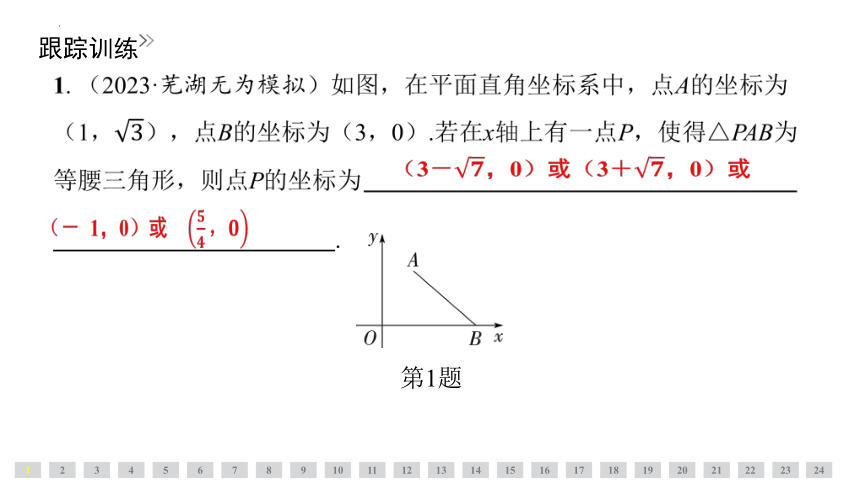
1. (2023·芜湖无为模拟)如图,在平面直角坐标系中,点A的坐标为(1,),点B的坐标为(3,0).若在x轴上有一点P,使得△PAB为等腰三角形,则点P的坐标为 (3-,0)或(3+,0)或(-1,0)或 .
第1题
(3-,0)或(3+,0)或
(- 1,0)或
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
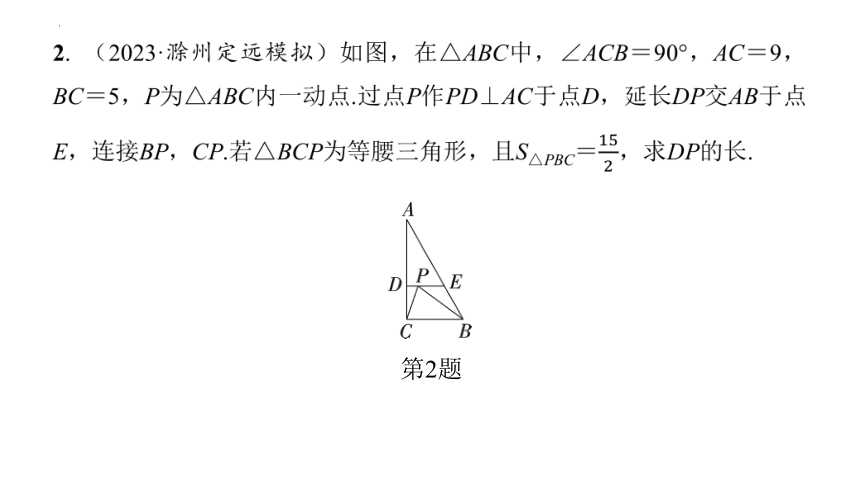
2. (2023·滁州定远模拟)如图,在△ABC中,∠ACB=90°,AC=9,BC=5,P为△ABC内一动点.过点P作PD⊥AC于点D,延长DP交AB于点E,连接BP,CP.若△BCP为等腰三角形,且S△PBC=,求DP的长.
第2题
解:∵ S△PBC=BC·CD=,BC=5,∴ CD=3.∴ AD=AC-CD=6.∵ PD⊥AC,∴ ∠EDA=90°=∠ACB.∴ DE∥BC. ∴ △ADE∽△ACB.∴ =.∴ =.∴ DE=.如图,过点P作PF⊥BC于点F,则∠PFC=∠ACB=∠CDE=90°.∴ 四边形CDPF是矩形.∴ PF=CD=3,DP=CF.① 如图①,当PB=BC=5时,在Rt△PBF中,BF==4.∴ DP=CF=BC-BF=1.∵ DP<DE.∴ 点P在线段DE上,符合题意.
第2题答案
第2题
② 如图②,当PC=PB时,DP=CF=BC=×5=.∵ DP<DE,∴ 点P在线段DE上,符合题意.③ 如图③,当PC=BC=5时,在Rt△CFP中,CF==4.∵ CF>DE,∴ 点P不存在.综上所述,DP的长为1或.
第2题答案
第2题
考向2:与直角三角形相关的分类讨论
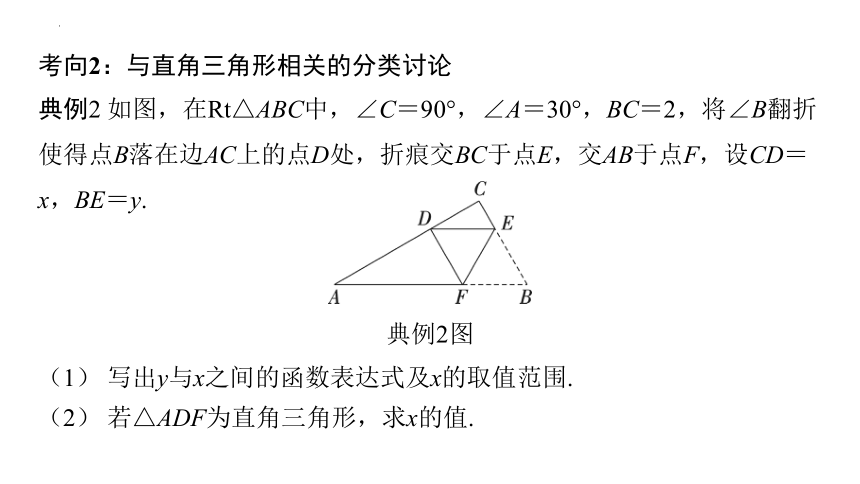
典例2 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,将∠B翻折使得点B落在边AC上的点D处,折痕交BC于点E,交AB于点F,设CD=x,BE=y.
典例2图
(1) 写出y与x之间的函数表达式及x的取值范围.
(2) 若△ADF为直角三角形,求x的值.
[思路点拨] (1) 根据折叠的性质得到DE=BE,根据勾股定理列式计算,得到答案;(2) 分∠ADF=90°,∠AFD=90°两种情况,根据勾股定理列出方程,解方程求出x的值.
解:(1) ∵ BE=y,BC=2,∴ CE=2-y.由折叠的性质,可知DE=BE=y.在Rt△DCE中,∵ CD2+CE2=DE2,∴ x2+(2-y)2=y2.整理,得y=x2+1(0<x<2).
典例2图
(2) 在Rt△ABC中,∵ ∠C=90°,∠A=30°,BC=2,∴ AB=2BC=4.由勾股定理,得AC===2.∴ AD=AC-CD=2-x.由折叠的性质,可知DF=BF.∴ AF=4-DF.当∠ADF=90°时,∵ ∠A=30°,∴ AF=2DF,即4-DF=2DF.∴ DF=.∴ AD=DF=.∴ 2-x=,解得x=.当∠AFD=90°时,∵ ∠A=30°,∴ AD=2DF.在Rt△ADF中,由勾股定理,得DF2+AF2=AD2,即DF2+(4-DF)2=(2DF)2,解得DF=2-2或DF=-2-2(不合题意,舍去).∴ AD=4-4.∴ 2-x=4-4,解得x=4-2.综上所述,若△ADF为直角三角形,则x的值为或4-2.
典例2图
跟踪训练
3. 如图,平面直角坐标系中有点A(-1,0),B(1,2).若在坐标轴上存在点P,使得△ABP为直角三角形,则满足条件的点P共有( C )
A. 2个 B. 4个
C. 6个 D. 7个
第3题
C
4. 如图,在△ABC中,AB=BC=2,AO=BO,M是线段CO的延长线上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为 或 .
第4题
或
类型2 对应关系不确定
考向1:全等三角形中的对应关系不确定
典例3 如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P以3cm/s的速度由点B向点C运动,同时点Q以相同的速度由点C向点A运动,当一个点到达终点时另一个点也随之停止运动.当△BPD与△CQP全等时,求点P运动的时间.
典例3图
[思路点拨] 当△BPD与△CQP全等时,根据∠B=∠C可知B和C是对应顶点,但这两个角的两边的对应关系不确定,应分两种情况讨论:① BD与CP是对应边;② BD与CQ是对应边.
解:∵ ∠B=∠C,∴ AB=AC.设点P,Q的运动时间为ts,则BP=3tcm,CQ=3tcm.∵ AB=10cm,BC=8cm,D为AB的中点,∴ BD=AB=×10=5(cm),PC=(8-3t)cm.① 当BD与CP是对应边时,△BPD≌△CQP.∴ BD=CP,BP=CQ.∴ 5=8-3t,3t=3t,解得t=1.② 当BD与CQ是对应边时,△BPD≌△CPQ.∴ BD=CQ,BP=CP.∴ 5=3t,3t=8-3t,无解.综上所述,当△BPD与△CQP全等时,点P运动的时间为1s.
典例3图
跟踪训练
5. 如图,点A的坐标为(-1,0),点B的坐标为(0,2).若在y轴的右侧有一点C使得△BOC与△BOA全等,则点C的坐标为 (1,0)或(1,2) .
第5题
(1,0)或
(1,2)
6. 如图,在△ABC中,AC⊥BC,AC=8,BC=4,AP⊥AC于点A,点D,E分别在AC和AP上运动,且DE=AB,当AD= 8或4 时,△ADE和△ABC全等.
第6题
8或4
考向2:相似三角形中的对应关系不确定
典例4 如图,正方形ABCD的边长为6,F为AB的中点,点E在AD上,且ED=2AE,在边CD上找一点P,连接EP,使△DEP与△AEF相似,则DP的长为 6或 .
典例4图
[思路点拨] 分△AEF∽△DEP和△AEF∽△DPE两种情况,利用相似三角形的性质求解即可.
6或
跟踪训练
7. 如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为线段AC上的动点,BC=4,AB=8,当△ABC和△AED相似时,AE的长为 2或 .
第7题
2或
8. 如图,CD=1,AE=2,CE=4,∠A=∠ECD,点B在AC的延长线上,当△BCD与△ACE相似时,BC的长为 2或 .
第8题
2或
类型3 点的位置不确定
考向1:与三角形相关的点的位置不确定
典例5 如图,∠ABC=∠ADE=90°,AB=BC,AD=DE,其中D是射线BC上一动点(点D不与点B,C重合),连接AC,EC,则∠DCE的度数为 135°或45° .
典例5图
135°或45°
[思路点拨] 分两种情况讨论:① 当点D在线段BC上时;② 当点D在线段BC的延长线上时.过点E作EF⊥BC,交BC的延长线于点F,根据全等三角形的性质即可求出∠DCE的度数.
跟踪训练
9. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,点C在直线l上.点P从点A出发,在△ABC的边上沿A→C→B向终点B运动,点Q从点B出发,在△ABC的边上沿B→C→A向终点A运动.点P的速度为每秒1个单位,点Q的速度为每秒2个单位.在运动过程中,若有一点先到达终点,则该点停止运动,另一个点继续运动,直到两点都到达相应的终点时整个运动才能停止.过点P作PE⊥l于点E,过点Q作QF⊥l于点F,则当点P的运动时间为 1秒或秒或6秒 时,△PEC与△CFQ全等.
1秒或秒或6秒
第9题
10. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D为AB的中点,F为AC上的动点,将△ADF沿直线DF折叠得到△EDF.若DE与△ABC的边垂直,则AF的长是多少?
第10题
解:在Rt△ABC中,∵ ∠A=30°,BC=2,∴ AB=4,AC=2.∵ D为AB的中点,∴ AD=BD=2.如图①,当DE⊥AC时,∠DGA=90°.由折叠可知,∠A=∠E=30°,AD=ED=2,EF=FA.∵ ∠DGA=90°,∴ ∠ADE=60°,AG=AD·cosA=.∵ ∠EDF=∠ADF,∴ ∠EDF=30°=∠E.∴ DF=EF=FA.∴ FG=EF=AF.∴ AG=AF+FG=AF+AF=.∴ AF=.
第10题答案
第10题
如图②,当DE⊥AB时,∠ADE=90°.由折叠可知,∠ADF=∠EDF=45°,∠A=∠E=30°.∴ ∠AGD=60°,∠EFG=30°=∠E.∴ GE=GF.在Rt△ADG中,AD=2,DG=AD·tan30°=,AG==.∴ GF=GE=DE-DG=AD-DG=2-. ∴ AF=AG-GF=-2+=2-2.
第10题答案
第10题
如图③,当DE⊥BC时,
∵ AC⊥BC,∴ DE∥AC.∴ ∠E=∠EFC.由折叠可知,AD=DE=2,∠E=∠A.∴ ∠EFC=∠A.∴ EF∥AD.又∵ DE∥AF,∴ 四边形ADEF是平行四边形.∴ AF=DE=2.综上所述,AF的长为或2-2或2.
第10题答案
第10题
考向2:与四边形相关的点的位置不确定
典例6 如图,正方形ABCD的边长为4,E是边AD的中点,连接BE,在线段BE上有一点P,如果点P到正方形一边的距离为1,那么PE的长为 或或 .
或或
典例6图
[思路点拨] 由勾股定理易得BE==2,由条件结合图形分类讨论,再利用平行线分线段成比例列出关系式,代入数值求解即可.
跟踪训练
11. 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=18cm,点P在边AD上以3cm/s的速度从点A向点D运动,点Q在边BC上以2cm/s的速度从点C向点B运动.若P,Q两点同时出发,则当直线PQ在四边形ABCD的内部截出一个平行四边形时,点P运动的时间为 2.4s或3.6s .
第11题
2.4s或3.6s
12. 如图,在矩形ABCD中,AD=18,AB=24,E为边DC上的一个动点,将矩形ABCD沿AE折叠,使点D落在点D'处,当△CD'E为直角三角形时,DE的长为 9或18 .
第12题
9或18
考向3:与圆相关的点的位置不确定
典例7 如图,PM,PN分别与☉O相切于点A,B,∠P=58°.若C为☉O上异于A,B的一点,连接AC,BC,则∠ACB的度数是 61°或119° .
典例7图
61°或119°
[思路点拨] 连接OA,OB,根据切线的性质得到OA⊥PA,OB⊥PB,进而求出∠AOB的度数,分点C在优弧AB上和点C在劣弧AB上这两种情况进行讨论,并根据圆周角定理计算即可.
跟踪训练
13. 如图,在☉O中,半径OA垂直于弦BC.若∠AOB=60°,D为☉O上一点,则∠ADC的度数为 30°或150° .
第13题
30°或150°
14. 如图,AB是☉O的直径,AB=2,直线l与☉O相切于点C,且l∥AB.在直线l上取一点D,连接AD交☉O于点E.若AE=DE,求CD的长.
第14题
解:① 如图①,当点D在点C的左侧时,连接OC,BE,BD,过点B作BF⊥l于点F.∵ AB是☉O的直径,∴ ∠AEB=90°,即BE⊥AD.∵ AE=DE,∴ BD=BA=2.∵ l与☉O相切于点C,∴ OC⊥l.∵ l∥AB,
∴ OC⊥AB.又∵ BF⊥l,∴ ∠OCF=∠COB=∠BFC=90°.∴ 四边形OCFB为矩形.∵ OB=OC,∴ 四边形OCFB为正方形.∴ CF=BF=OC=1.∴ DF==.∴ CD=DF-CF=-1.
第14题答案
第14题
② 如图②,当点D在点C的右侧时,连接OC,BE,BD,过点B作BF⊥l于点F.∵ AB是☉O的直径,∴ ∠AEB=90°,即BE⊥AD.∵ AE=DE,∴ BD=BA=2.∵ l与☉O相切于点C,∴ OC⊥l.∵ l∥AB,∴ OC⊥AB.∵ BF⊥l,∴ ∠OCF=∠COB=∠BFC=90°.∴ 四边形OCFB为矩形.∵ OB=OC,
∴ 四边形OCFB为正方形.∴ CF=BF=OC=1.∴ DF==.∴ CD=DF+CF=+1.综上所述,CD的长是+1或-1.
第14题答案
第14题
强化练习
1. 如图,在△ABC中,∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿AB移动到点B,则当点P出发 2.5或4 s时,△ACP是等腰三角形.
第1题
2.5或4
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,在正方形ABCD中,边长为6,E是边CD的中点,对角线BD上有一动点F,则当△ABF与△DEF相似时,BF的长为 6或8 .
第2题
6或8
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在平面直角坐标系中,点A的坐标为(-12,5),过点A作AB⊥x轴于点B,C是x轴负半轴上的一个动点,D是y轴正半轴上的一个动点,且始终保持CD=OA,则当点D的坐标为 (0,12)或(0,5) 时,△ABO与△OCD全等.
第3题
(0,12)或(0,5)
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,△ABC是等边三角形,AB=4,AD是边BC上的高,E是射线AC上的动点,连接BE,交直线AD于点P,则当△ADE是等腰三角形时,AP的长为 或24-12或 .
第4题
或24-12或
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,在△ABC中,∠A=60°,∠C=50°,D是线段AC上的一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点C'处,则当C'D平行于△ABC的边时,∠CDB的度数为 65°或120° .
第5题
65°或120°
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,AE是△ABC的中线,动点P从点A出发,以3cm/s的速度沿A→C→E运动,最终到达点E,则当点P运动 或 s时,△APE的面积为9cm2.
第6题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在矩形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿B→C→D→A运动,则当点P运动 1或7 秒时,△ABP和△DCE全等.
第7题
1或7
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,∠AOB=60°,半径为3cm的☉P沿边OA从右向左平行移动,与边OA相切的切点记为C,☉P移动到与边OB相交于点E,F.若EF=4cm,则OC的长为 或 cm.
第8题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 如图,在△ABC中,∠A=90°,AB=AC=,D,E分别为边AC,BC上的点,将△CDE沿DE折叠,使点C的对应点C'落在射线CA上,连接BC',则当Rt△ABC'的某一直角边的长等于斜边BC'长的一半时,CD的长为 或 .
第9题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,矩形ABCD的边AB的长为6,将△ACD沿对角线AC翻折得到△ACD',CD'与AB交于点E,再以CD'为折痕,将△BCE进行翻折,得到△B'CE.若两次翻折后,点B'恰好落在△ACD的边上,则AD的长为 2或6-6 .
第10题
2或6-6
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 如图,在矩形ABCD中,AB=4cm,AD=7cm,点E在边AD上运动,将△CDE沿CE折叠,使点D落在点D'处.若△CDE有两条边存在2倍的数量关系,则点D'到AD的距离为 2或或6 cm.
第11题
2或或6
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,D是等边三角形ABC内的一点,E是△ABC外的一点,∠CDB=130°,∠ADB=α,△ABD≌△ACE.
(1) 求证:△ADE是等边三角形.
解:(1) ∵ △ABC为等边三角形,∴ ∠BAC=60°.
∵ △ABD≌△ACE,∴ AD=AE,∠BAD=∠CAE.
∴ ∠BAD+∠CAD=∠CAE+∠CAD=∠DAE=60°.
∴ △ADE是等边三角形
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 若△CDE是直角三角形,求α的度数.
解:(2) ∵ △ABD≌△ACE,∴ ∠AEC=∠ADB=α.
∵ △ADE是等边三角形,∴ ∠AED=∠ADE=60°.
∴ ∠CED=α-60°,∠CDE=360°-130°-α-60°=170°-α.∴ ∠DCE=180°-∠CED-∠CDE=180°-(α-60°)-(170°-α)=70°.当∠CED=90°时,α-60°=90°,
∴ α=150°.当∠CDE=90°时,170°-α=90°,∴ α=80°.综上所述,α的度数为150°或80°
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,在平面直角坐标系中,OA=OB=4,BC=12,点P的坐标为(a,6).
(1) 求点A,C的坐标.
解:(1) ∵ OA=OB=4,BC=12,∴ 点A的坐标为(0,4),OC=12-4=8.∴ 点C的坐标为(8,0)
第13题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 是否存在点P,使△PAB的面积等于△ABC的面积?若存在,请求出点P的坐标;若不存在,请说明理由.
第13题
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(2) 存在 ∵ 点P的坐标为(a,6),∴ 点P在直线y=6上运动.分两种情况讨论:① 如图①,当点P在y轴左侧时,a<0,连接OP.∵ S△PAB=S△BOP+S△OAP-S△AOB,S△PAB=S△ABC,∴ ×4×6+×4×(-a)-×4×4=×12×4,解得a=-10.∴ 点P的坐标为(-10,6).② 如图②,当点P在y轴右侧时,a>0,连接OP.∵ S△PAB=S△AOB+SAOP-S△BOP,S△PAB=S△ABC,∴ ×4×4+×4×a-×4×6=×12×4,解得a=14.∴ 点P的坐标为(14,6).综上所述,存在点P,使△PAB的面积等于△ABC的面积,点P的坐标为(-10,6)或(14,6)
1
2
3
4
5
6
7
8
9
10
11
12
13
专题三 多解问题
类型1 特殊三角形中的多解题
考向1:与等腰三角形相关的分类讨论
典例1 (2023·阜阳模拟)如图,在△ABC中,AB=AC=8,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=∠B,DE与AC交于点E.
典例1图
(1) 求证:△ABD∽△DCE.
(2) 若∠B=40°,当∠ADB的度数为多少时,△ADE是等腰三角形?
[思路点拨] (1) 根据三角形外角的性质证明∠BAD=∠CDE,再根据等腰三角形的性质证明∠B=∠C,即可证明△ABD∽△DCE.(2) 分三种情况:DA=DE;AD=AE;EA=ED.根据等腰三角形的性质分别求出∠ADB的度数即可.
解:(1) ∵ ∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠ADE=∠B,∴ ∠BAD=∠CDE.∵ AB=AC,∴ ∠B=∠C.
∴ △ABD∽△DCE.
典例1图
(2) 当DA=DE时,∠DEA=∠DAE.∵ ∠ADE=∠B=∠C=40°,
∴ ∠DAE=∠DEA=×(180°-40°)=70°.∴ ∠ADB=∠DAE+∠C=110°.当AD=AE时,∠DEA=∠ADE=∠B=40°=∠C.此时点D与点B重合,不合题意.当EA=ED时,∠EAD=∠ADE=∠B=40°.∴ ∠ADB=∠EAD+∠C=80°.综上所述,当∠ADB的度数为110°或80°时,△ADE是等腰三角形.
典例1图
跟踪训练
1. (2023·芜湖无为模拟)如图,在平面直角坐标系中,点A的坐标为(1,),点B的坐标为(3,0).若在x轴上有一点P,使得△PAB为等腰三角形,则点P的坐标为 (3-,0)或(3+,0)或(-1,0)或 .
第1题
(3-,0)或(3+,0)或
(- 1,0)或
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2. (2023·滁州定远模拟)如图,在△ABC中,∠ACB=90°,AC=9,BC=5,P为△ABC内一动点.过点P作PD⊥AC于点D,延长DP交AB于点E,连接BP,CP.若△BCP为等腰三角形,且S△PBC=,求DP的长.
第2题
解:∵ S△PBC=BC·CD=,BC=5,∴ CD=3.∴ AD=AC-CD=6.∵ PD⊥AC,∴ ∠EDA=90°=∠ACB.∴ DE∥BC. ∴ △ADE∽△ACB.∴ =.∴ =.∴ DE=.如图,过点P作PF⊥BC于点F,则∠PFC=∠ACB=∠CDE=90°.∴ 四边形CDPF是矩形.∴ PF=CD=3,DP=CF.① 如图①,当PB=BC=5时,在Rt△PBF中,BF==4.∴ DP=CF=BC-BF=1.∵ DP<DE.∴ 点P在线段DE上,符合题意.
第2题答案
第2题
② 如图②,当PC=PB时,DP=CF=BC=×5=.∵ DP<DE,∴ 点P在线段DE上,符合题意.③ 如图③,当PC=BC=5时,在Rt△CFP中,CF==4.∵ CF>DE,∴ 点P不存在.综上所述,DP的长为1或.
第2题答案
第2题
考向2:与直角三角形相关的分类讨论
典例2 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,将∠B翻折使得点B落在边AC上的点D处,折痕交BC于点E,交AB于点F,设CD=x,BE=y.
典例2图
(1) 写出y与x之间的函数表达式及x的取值范围.
(2) 若△ADF为直角三角形,求x的值.
[思路点拨] (1) 根据折叠的性质得到DE=BE,根据勾股定理列式计算,得到答案;(2) 分∠ADF=90°,∠AFD=90°两种情况,根据勾股定理列出方程,解方程求出x的值.
解:(1) ∵ BE=y,BC=2,∴ CE=2-y.由折叠的性质,可知DE=BE=y.在Rt△DCE中,∵ CD2+CE2=DE2,∴ x2+(2-y)2=y2.整理,得y=x2+1(0<x<2).
典例2图
(2) 在Rt△ABC中,∵ ∠C=90°,∠A=30°,BC=2,∴ AB=2BC=4.由勾股定理,得AC===2.∴ AD=AC-CD=2-x.由折叠的性质,可知DF=BF.∴ AF=4-DF.当∠ADF=90°时,∵ ∠A=30°,∴ AF=2DF,即4-DF=2DF.∴ DF=.∴ AD=DF=.∴ 2-x=,解得x=.当∠AFD=90°时,∵ ∠A=30°,∴ AD=2DF.在Rt△ADF中,由勾股定理,得DF2+AF2=AD2,即DF2+(4-DF)2=(2DF)2,解得DF=2-2或DF=-2-2(不合题意,舍去).∴ AD=4-4.∴ 2-x=4-4,解得x=4-2.综上所述,若△ADF为直角三角形,则x的值为或4-2.
典例2图
跟踪训练
3. 如图,平面直角坐标系中有点A(-1,0),B(1,2).若在坐标轴上存在点P,使得△ABP为直角三角形,则满足条件的点P共有( C )
A. 2个 B. 4个
C. 6个 D. 7个
第3题
C
4. 如图,在△ABC中,AB=BC=2,AO=BO,M是线段CO的延长线上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为 或 .
第4题
或
类型2 对应关系不确定
考向1:全等三角形中的对应关系不确定
典例3 如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P以3cm/s的速度由点B向点C运动,同时点Q以相同的速度由点C向点A运动,当一个点到达终点时另一个点也随之停止运动.当△BPD与△CQP全等时,求点P运动的时间.
典例3图
[思路点拨] 当△BPD与△CQP全等时,根据∠B=∠C可知B和C是对应顶点,但这两个角的两边的对应关系不确定,应分两种情况讨论:① BD与CP是对应边;② BD与CQ是对应边.
解:∵ ∠B=∠C,∴ AB=AC.设点P,Q的运动时间为ts,则BP=3tcm,CQ=3tcm.∵ AB=10cm,BC=8cm,D为AB的中点,∴ BD=AB=×10=5(cm),PC=(8-3t)cm.① 当BD与CP是对应边时,△BPD≌△CQP.∴ BD=CP,BP=CQ.∴ 5=8-3t,3t=3t,解得t=1.② 当BD与CQ是对应边时,△BPD≌△CPQ.∴ BD=CQ,BP=CP.∴ 5=3t,3t=8-3t,无解.综上所述,当△BPD与△CQP全等时,点P运动的时间为1s.
典例3图
跟踪训练
5. 如图,点A的坐标为(-1,0),点B的坐标为(0,2).若在y轴的右侧有一点C使得△BOC与△BOA全等,则点C的坐标为 (1,0)或(1,2) .
第5题
(1,0)或
(1,2)
6. 如图,在△ABC中,AC⊥BC,AC=8,BC=4,AP⊥AC于点A,点D,E分别在AC和AP上运动,且DE=AB,当AD= 8或4 时,△ADE和△ABC全等.
第6题
8或4
考向2:相似三角形中的对应关系不确定
典例4 如图,正方形ABCD的边长为6,F为AB的中点,点E在AD上,且ED=2AE,在边CD上找一点P,连接EP,使△DEP与△AEF相似,则DP的长为 6或 .
典例4图
[思路点拨] 分△AEF∽△DEP和△AEF∽△DPE两种情况,利用相似三角形的性质求解即可.
6或
跟踪训练
7. 如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为线段AC上的动点,BC=4,AB=8,当△ABC和△AED相似时,AE的长为 2或 .
第7题
2或
8. 如图,CD=1,AE=2,CE=4,∠A=∠ECD,点B在AC的延长线上,当△BCD与△ACE相似时,BC的长为 2或 .
第8题
2或
类型3 点的位置不确定
考向1:与三角形相关的点的位置不确定
典例5 如图,∠ABC=∠ADE=90°,AB=BC,AD=DE,其中D是射线BC上一动点(点D不与点B,C重合),连接AC,EC,则∠DCE的度数为 135°或45° .
典例5图
135°或45°
[思路点拨] 分两种情况讨论:① 当点D在线段BC上时;② 当点D在线段BC的延长线上时.过点E作EF⊥BC,交BC的延长线于点F,根据全等三角形的性质即可求出∠DCE的度数.
跟踪训练
9. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,点C在直线l上.点P从点A出发,在△ABC的边上沿A→C→B向终点B运动,点Q从点B出发,在△ABC的边上沿B→C→A向终点A运动.点P的速度为每秒1个单位,点Q的速度为每秒2个单位.在运动过程中,若有一点先到达终点,则该点停止运动,另一个点继续运动,直到两点都到达相应的终点时整个运动才能停止.过点P作PE⊥l于点E,过点Q作QF⊥l于点F,则当点P的运动时间为 1秒或秒或6秒 时,△PEC与△CFQ全等.
1秒或秒或6秒
第9题
10. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D为AB的中点,F为AC上的动点,将△ADF沿直线DF折叠得到△EDF.若DE与△ABC的边垂直,则AF的长是多少?
第10题
解:在Rt△ABC中,∵ ∠A=30°,BC=2,∴ AB=4,AC=2.∵ D为AB的中点,∴ AD=BD=2.如图①,当DE⊥AC时,∠DGA=90°.由折叠可知,∠A=∠E=30°,AD=ED=2,EF=FA.∵ ∠DGA=90°,∴ ∠ADE=60°,AG=AD·cosA=.∵ ∠EDF=∠ADF,∴ ∠EDF=30°=∠E.∴ DF=EF=FA.∴ FG=EF=AF.∴ AG=AF+FG=AF+AF=.∴ AF=.
第10题答案
第10题
如图②,当DE⊥AB时,∠ADE=90°.由折叠可知,∠ADF=∠EDF=45°,∠A=∠E=30°.∴ ∠AGD=60°,∠EFG=30°=∠E.∴ GE=GF.在Rt△ADG中,AD=2,DG=AD·tan30°=,AG==.∴ GF=GE=DE-DG=AD-DG=2-. ∴ AF=AG-GF=-2+=2-2.
第10题答案
第10题
如图③,当DE⊥BC时,
∵ AC⊥BC,∴ DE∥AC.∴ ∠E=∠EFC.由折叠可知,AD=DE=2,∠E=∠A.∴ ∠EFC=∠A.∴ EF∥AD.又∵ DE∥AF,∴ 四边形ADEF是平行四边形.∴ AF=DE=2.综上所述,AF的长为或2-2或2.
第10题答案
第10题
考向2:与四边形相关的点的位置不确定
典例6 如图,正方形ABCD的边长为4,E是边AD的中点,连接BE,在线段BE上有一点P,如果点P到正方形一边的距离为1,那么PE的长为 或或 .
或或
典例6图
[思路点拨] 由勾股定理易得BE==2,由条件结合图形分类讨论,再利用平行线分线段成比例列出关系式,代入数值求解即可.
跟踪训练
11. 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=18cm,点P在边AD上以3cm/s的速度从点A向点D运动,点Q在边BC上以2cm/s的速度从点C向点B运动.若P,Q两点同时出发,则当直线PQ在四边形ABCD的内部截出一个平行四边形时,点P运动的时间为 2.4s或3.6s .
第11题
2.4s或3.6s
12. 如图,在矩形ABCD中,AD=18,AB=24,E为边DC上的一个动点,将矩形ABCD沿AE折叠,使点D落在点D'处,当△CD'E为直角三角形时,DE的长为 9或18 .
第12题
9或18
考向3:与圆相关的点的位置不确定
典例7 如图,PM,PN分别与☉O相切于点A,B,∠P=58°.若C为☉O上异于A,B的一点,连接AC,BC,则∠ACB的度数是 61°或119° .
典例7图
61°或119°
[思路点拨] 连接OA,OB,根据切线的性质得到OA⊥PA,OB⊥PB,进而求出∠AOB的度数,分点C在优弧AB上和点C在劣弧AB上这两种情况进行讨论,并根据圆周角定理计算即可.
跟踪训练
13. 如图,在☉O中,半径OA垂直于弦BC.若∠AOB=60°,D为☉O上一点,则∠ADC的度数为 30°或150° .
第13题
30°或150°
14. 如图,AB是☉O的直径,AB=2,直线l与☉O相切于点C,且l∥AB.在直线l上取一点D,连接AD交☉O于点E.若AE=DE,求CD的长.
第14题
解:① 如图①,当点D在点C的左侧时,连接OC,BE,BD,过点B作BF⊥l于点F.∵ AB是☉O的直径,∴ ∠AEB=90°,即BE⊥AD.∵ AE=DE,∴ BD=BA=2.∵ l与☉O相切于点C,∴ OC⊥l.∵ l∥AB,
∴ OC⊥AB.又∵ BF⊥l,∴ ∠OCF=∠COB=∠BFC=90°.∴ 四边形OCFB为矩形.∵ OB=OC,∴ 四边形OCFB为正方形.∴ CF=BF=OC=1.∴ DF==.∴ CD=DF-CF=-1.
第14题答案
第14题
② 如图②,当点D在点C的右侧时,连接OC,BE,BD,过点B作BF⊥l于点F.∵ AB是☉O的直径,∴ ∠AEB=90°,即BE⊥AD.∵ AE=DE,∴ BD=BA=2.∵ l与☉O相切于点C,∴ OC⊥l.∵ l∥AB,∴ OC⊥AB.∵ BF⊥l,∴ ∠OCF=∠COB=∠BFC=90°.∴ 四边形OCFB为矩形.∵ OB=OC,
∴ 四边形OCFB为正方形.∴ CF=BF=OC=1.∴ DF==.∴ CD=DF+CF=+1.综上所述,CD的长是+1或-1.
第14题答案
第14题
强化练习
1. 如图,在△ABC中,∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿AB移动到点B,则当点P出发 2.5或4 s时,△ACP是等腰三角形.
第1题
2.5或4
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,在正方形ABCD中,边长为6,E是边CD的中点,对角线BD上有一动点F,则当△ABF与△DEF相似时,BF的长为 6或8 .
第2题
6或8
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在平面直角坐标系中,点A的坐标为(-12,5),过点A作AB⊥x轴于点B,C是x轴负半轴上的一个动点,D是y轴正半轴上的一个动点,且始终保持CD=OA,则当点D的坐标为 (0,12)或(0,5) 时,△ABO与△OCD全等.
第3题
(0,12)或(0,5)
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,△ABC是等边三角形,AB=4,AD是边BC上的高,E是射线AC上的动点,连接BE,交直线AD于点P,则当△ADE是等腰三角形时,AP的长为 或24-12或 .
第4题
或24-12或
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,在△ABC中,∠A=60°,∠C=50°,D是线段AC上的一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点C'处,则当C'D平行于△ABC的边时,∠CDB的度数为 65°或120° .
第5题
65°或120°
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,AE是△ABC的中线,动点P从点A出发,以3cm/s的速度沿A→C→E运动,最终到达点E,则当点P运动 或 s时,△APE的面积为9cm2.
第6题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在矩形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿B→C→D→A运动,则当点P运动 1或7 秒时,△ABP和△DCE全等.
第7题
1或7
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,∠AOB=60°,半径为3cm的☉P沿边OA从右向左平行移动,与边OA相切的切点记为C,☉P移动到与边OB相交于点E,F.若EF=4cm,则OC的长为 或 cm.
第8题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 如图,在△ABC中,∠A=90°,AB=AC=,D,E分别为边AC,BC上的点,将△CDE沿DE折叠,使点C的对应点C'落在射线CA上,连接BC',则当Rt△ABC'的某一直角边的长等于斜边BC'长的一半时,CD的长为 或 .
第9题
或
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,矩形ABCD的边AB的长为6,将△ACD沿对角线AC翻折得到△ACD',CD'与AB交于点E,再以CD'为折痕,将△BCE进行翻折,得到△B'CE.若两次翻折后,点B'恰好落在△ACD的边上,则AD的长为 2或6-6 .
第10题
2或6-6
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 如图,在矩形ABCD中,AB=4cm,AD=7cm,点E在边AD上运动,将△CDE沿CE折叠,使点D落在点D'处.若△CDE有两条边存在2倍的数量关系,则点D'到AD的距离为 2或或6 cm.
第11题
2或或6
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,D是等边三角形ABC内的一点,E是△ABC外的一点,∠CDB=130°,∠ADB=α,△ABD≌△ACE.
(1) 求证:△ADE是等边三角形.
解:(1) ∵ △ABC为等边三角形,∴ ∠BAC=60°.
∵ △ABD≌△ACE,∴ AD=AE,∠BAD=∠CAE.
∴ ∠BAD+∠CAD=∠CAE+∠CAD=∠DAE=60°.
∴ △ADE是等边三角形
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 若△CDE是直角三角形,求α的度数.
解:(2) ∵ △ABD≌△ACE,∴ ∠AEC=∠ADB=α.
∵ △ADE是等边三角形,∴ ∠AED=∠ADE=60°.
∴ ∠CED=α-60°,∠CDE=360°-130°-α-60°=170°-α.∴ ∠DCE=180°-∠CED-∠CDE=180°-(α-60°)-(170°-α)=70°.当∠CED=90°时,α-60°=90°,
∴ α=150°.当∠CDE=90°时,170°-α=90°,∴ α=80°.综上所述,α的度数为150°或80°
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,在平面直角坐标系中,OA=OB=4,BC=12,点P的坐标为(a,6).
(1) 求点A,C的坐标.
解:(1) ∵ OA=OB=4,BC=12,∴ 点A的坐标为(0,4),OC=12-4=8.∴ 点C的坐标为(8,0)
第13题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 是否存在点P,使△PAB的面积等于△ABC的面积?若存在,请求出点P的坐标;若不存在,请说明理由.
第13题
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(2) 存在 ∵ 点P的坐标为(a,6),∴ 点P在直线y=6上运动.分两种情况讨论:① 如图①,当点P在y轴左侧时,a<0,连接OP.∵ S△PAB=S△BOP+S△OAP-S△AOB,S△PAB=S△ABC,∴ ×4×6+×4×(-a)-×4×4=×12×4,解得a=-10.∴ 点P的坐标为(-10,6).② 如图②,当点P在y轴右侧时,a>0,连接OP.∵ S△PAB=S△AOB+SAOP-S△BOP,S△PAB=S△ABC,∴ ×4×4+×4×a-×4×6=×12×4,解得a=14.∴ 点P的坐标为(14,6).综上所述,存在点P,使△PAB的面积等于△ABC的面积,点P的坐标为(-10,6)或(14,6)
1
2
3
4
5
6
7
8
9
10
11
12
13
同课章节目录
