2024年中考数学二轮复习突破课件:专题四 二次函数综合题(共63张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习突破课件:专题四 二次函数综合题(共63张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:41:19 | ||
图片预览









文档简介
(共63张PPT)
专题四 二次函数综合题
类型1 与线段有关的问题(含最值)
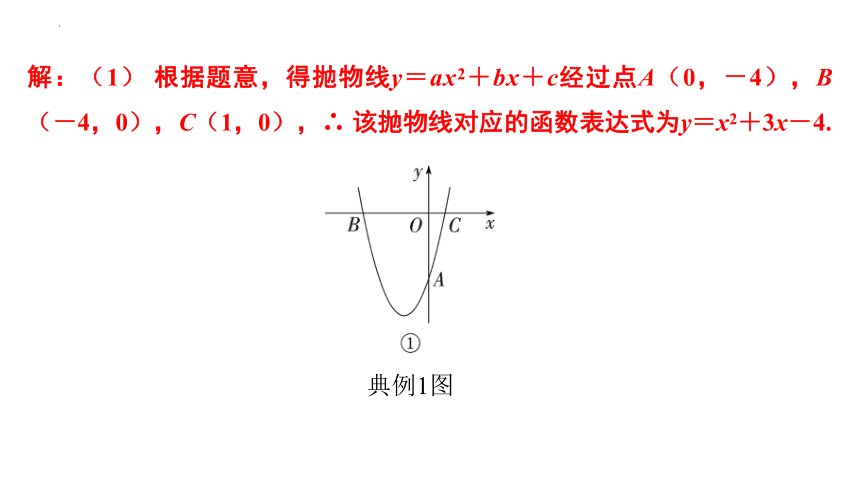
典例1 如图①,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(-4,0),C(1,0)两点,与y轴交于点A(0,-4).
典例1图
(1) 求该抛物线对应的函数表达式.
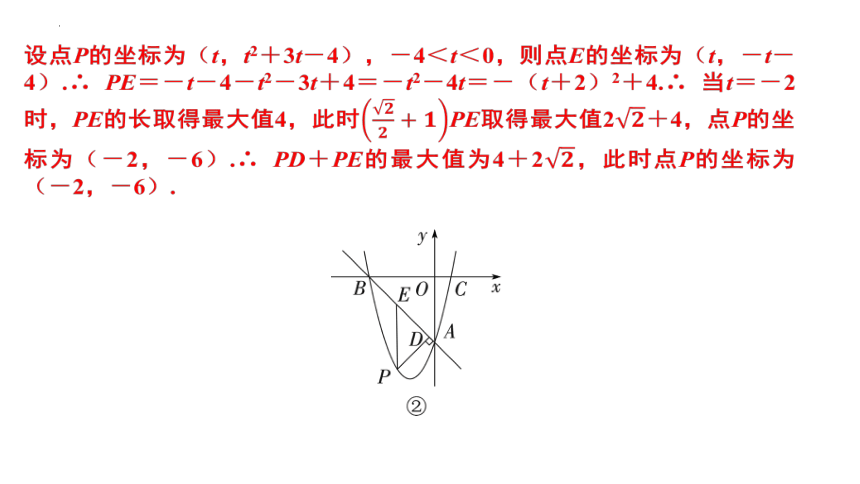
(2) 如图②,作直线AB,P是直线AB下方抛物线上的动点,过点P作y轴的平行线交AB于点E,过点P作PD⊥AB于点D.求PD+PE的最大值及此时点P的坐标.
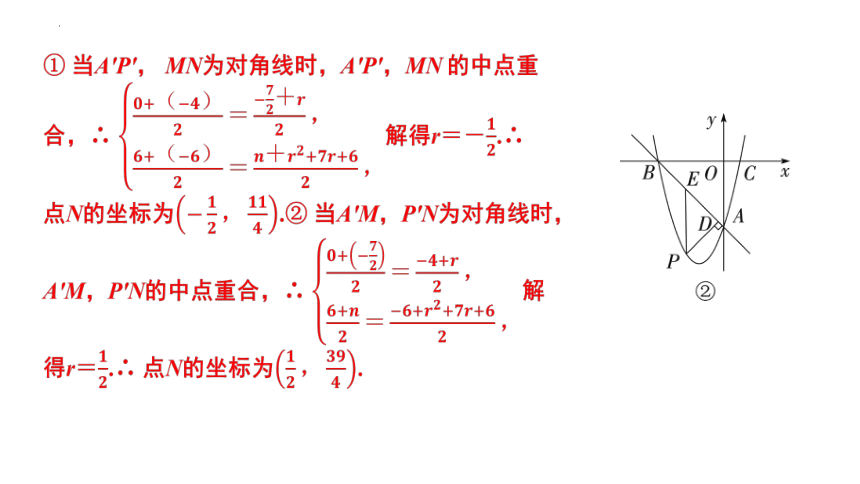
(3) 在(2)中PD+PE取得最大值的条件下,将该抛物线向左平移2个单位,P'为点P的对应点,平移后的抛物线与y轴交于点A',M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点P',A',M,N为顶点的四边形是平行四边形,直接写出所有符合条件的点N的坐标.
[思路点拨] (1) 将A(0,-4),B(-4,0),C(1,0)代入y=ax2+bx+c即可建立方程组求解.(2) 先求出直线AB对应的函数表达式,设点P的坐标为(t,t2+3t-4),则点E的坐标为(t,-t-4).建立PD+PE与t之间的函数表达式即可求解.(3) 根据平移确定新抛物线对应的函数表达式,进而可求出点A'的坐标,以平行四边形的对角线为切入点,根据“平行四边形的对角线互相平分”即可求解.
解:(1) 根据题意,得抛物线y=ax2+bx+c经过点A(0,-4),B(-4,0),C(1,0),∴ 该抛物线对应的函数表达式为y=x2+3x-4.
典例1图
(2) 设直线AB对应的函数表达式为y=kx+b1.∵ 点A(0,-4),B(-4,0)在直线AB上,∴ 解得∴ 直线AB对应的函数表达式为y=-x-4.∵ PE∥y 轴,且PD⊥AB,∴ 易得∠DPE=∠ABC.∴ PD=PE·cos∠DPE=PE·cos∠ABC.∵ OA=OB=4,∠AOB=90°,∴ ∠ABC=45°.∴ PD=PE.∴ PD+PE=PE+PE=PE.
设点P的坐标为(t,t2+3t-4),-4<t<0,则点E的坐标为(t,-t-4).∴ PE=-t-4-t2-3t+4=-t2-4t=-(t+2)2+4.∴ 当t=-2时,PE的长取得最大值4,此时PE取得最大值2+4,点P的坐标为(-2,-6).∴ PD+PE的最大值为4+2,此时点P的坐标为(-2,-6).
(3) ∵ 将抛物线y=x2+3x-4向左平移2个单位得抛物线y=(x+2)2+3(x+2)-4=x2+7x+6,∴ 新抛物线的对称轴是直线x=-=-.在y=x2+7x+6中,令x=0,得y=6.∴ 点A'的坐标为(0,6).将点P(-2,-6)向左平移2个单位得点P'(-4,-6).设点M,N(r,r2+7r+6).分三种情况讨论:
① 当A'P', MN为对角线时,A'P',MN 的中点重合,∴ 解得r=-.∴ 点N的坐标为.② 当A'M,P'N为对角线时,A'M,P'N的中点重合,∴ 解得r=.∴ 点N的坐标为.
③ 当A'N,P'M为对角线时,A'N,P'M的中点重合,解得r=-.∴ 点N的坐标为.综上所述,符合条件的点N的坐标为或或.
跟踪训练
1. (2023·合肥庐江二模)如图,直线m:y=b和直线n:y=x-b分别与y轴交于点A,B,顶点为C的抛物线L:y=-x2+bx与x轴的右交点为D.
(1) 若AB=8,求b的值和抛物线L的对称轴.
解:(1) 在y=x-b中,令x=0,得y=-b.∴ 点B(0,-b).∵ AB=8,点A(0,b),∴ b-(-b)=8,解得b=4.∴ 抛物线L对应的函数表达式为y=-x2+4x=-(x-2)2+4.∴ 抛物线L的对称轴为直线x=2.
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(2) 当顶点C在直线m下方时,求顶点C到直线m的距离的最大值.
解:解:(2) ∵ y=-x2+bx=-+,∴ 抛物线L的顶点C的坐标为.∵ 点C在直线m下方,
∴ 点C到直线m的距离为b-=-(b-2)2+1.∵ -<0,∴ 当b=2时,b-取得最大值1.∴ 顶点C到直线m距离的最大值为1.
第1题
(3) 在抛物线L和直线n所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“整点”.当b=2023时,求“整点”的个数.
解:解:(3) 当b=2023时,抛物线L对应的函数表达式为y=-x2+2023x,直线n对应的函数表达式为y=x-2023.令-x2+2023x=x-2023,即x2-2022x-2023=0,解得x1=-1,x2=2023.∵ 对y=-x2+2023x和y=x-2023,每一个整数x的值都对应一个整数y的值,且-1和2023之间(不包括-1和2023)共有2023个整数,∴ “整点”的个数为2023×2+2=4048.
第1题
类型2 与面积有关的问题(含最值)
典例2 (2023·芜湖一模)如图,抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-1,0),直线y=kx+3经过点B,C.
典例2图
(1) 抛物线对应的函数表达式为 y=-x2+2x+3 ,直线BC对应的函数表达式为 y=-x+3 .
(2) D是第一象限内抛物线上的一个动点,过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD.设点D的横坐标为m,△BCD的面积为S,求S关于m的函数表达式及自变量m的取值范围,并求出S的最大值.
(3) 已知M为抛物线对称轴上的一个动点,若△MBC是以BC为直角边的直角三角形,请直接写出点M的坐标.
y=-x2+2x+3
y=-x+3
[思路点拨] (1) 根据直线y=kx+3经过点C,点C在y轴上,可求得点C的坐标,从而得到c的值,将点A的坐标代入抛物线对应的函数表达式即可求解.再求出点B的坐标,从而求得直线BC对应的函数表达式.(2) 根据题意,可得点D(m,-m2+2m+3),E(m,-m+3),则DE=-m2+3m.再由S△BCD=DE·OB求出S关于m的函数表达式,由二次函数的性质即可求出S的最大值.(3) 分MC是斜边、MB是斜边两种情况,分别求解即可.
解:(2) 由题意可知,点D(m,-m2+2m+3),E(m,-m+3).∴ DE=(-m2+2m+3)-(-m+3)=-m2+3m.由B(3,0)可知,OB=3.∵ S△BCD=DE·OB,∴ S=(-m2+3m)=-m2+m=
-+(0<m<3).∵ -<0,∴ 当m=时,S有最大值,最大值为.∴ S关于m的函数表达式为S=-m2+m(0<m<3),S的最大值为.
典例2图
(3) 抛物线y=-x2+2x+3的对称轴为直线x=1.根据题意,设点M(1,a),则MB2=a2+4,MC2=1+(a-3)2,BC2=18.① 当MC是斜边时,MC2=MB2+BC2,即1+(a-3)2=a2+4+18,解得a=-2.∴ 点M(1,-2).② 当MB是斜边时,MB2=MC2+BC2,即a2+4=1+(a-3)2+18,解得a=4.∴ 点M(1,4).综上所述,点M的坐标为(1,-2)或(1,4).
典例2图
跟踪训练
2. (2023·滁州来安二模)如图①,一块钢板截面的一边为线段AB,另一边曲线ACB为抛物线的一部分,现沿线段BC将这块钢板分成甲、乙两部分,以边AB所在直线为x轴,经过点C且与AB垂直的直线为y轴,建立平面直角坐标系,O为原点.已知OA=2米,OB=8米,OC=6米.
第2题
(1) 求曲线ACB所在抛物线对应的函数表达式(不用写出自变量的取值范围).
解:(1) ∵ OC=6米,∴ 可设曲线ACB所在抛物线对应的函数表达式为y=ax2+bx+6.∵ OA=2米,OB=8米,∴ 点A的坐标为(-2,0),点B的坐标为(8,0).∵ 点A,B在曲线ACB所在的抛物线上,
∴ 解得∴ 曲线ACB所在抛物线对应的函数表达式为y=-x2+x+6.
(2) 如图②,在这块钢板的甲部分中截取一个矩形DEFG,其中D为BC的中点,点E,F均在线段AB上,点G在曲线AC上.求EF的长.
解:(2) ∵ 点B(8,0),C(0,6),D为BC的中点,∴ 点D的坐标为(4,3).∴ 点E的坐标为(4,0).当y=3时,-x2+x+6=3,解得x1=3+,x2=3-.∴ 结合题图可知,点G的横坐标为3-.∵ 四边形DEFG是矩形,∴ DE⊥x轴,GF⊥x轴.∴ 点F的坐标为(3-,0).∴ EF=4-(3-)=(+1)米.
(3) 如图③,在这块钢板的乙部分中截取一个△PBC,其中点P在曲线BC上,记△PBC的面积为S平方米.求S的最大值.
解:(3) 设直线BC对应的函数表达式为y=kx+c(k≠0).∵ 点B(8,0),C(0,6)在直线BC上,∴ 解得
∴ 直线BC对应的函数表达式为y=-x+6.
∵ 点P在抛物线上,∴ 设点P的坐标为,0<m<8.如图③,过点P作PH⊥x轴于点H,交BC于点Q,则PH∥y轴,点Q的坐标为(m,-m+6).∴ QP=-m2+m+6-(-m+6)=-m2+3m.∵ S△PBC=S△CPQ+S△BPQ=QP·OB,∴ S=·8=
-m2+12m=-(m-4)2+24.∵ -<0,0<m<8,∴ 当m=4时,S取得最大值,最大值为24.
类型3 含字母系数的二次函数问题
典例3 (2023·芜湖南陵模拟)已知抛物线y=x2-2mx+m2-2与直线x=-2交于点P.
(1) 当抛物线经过点(-1,-2)时,求抛物线对应的函数表达式.
(2) 设点P的纵坐标为yP,当yP取最小值时,抛物线上有两点(x1,y1),(x2,y2),x1<x2<-2,比较y1与y2的大小.
(3) 若线段AB的两个端点分别是A(0,2),B(2,2),当抛物线与线段AB有公共点时,求出m的取值范围.
[思路点拨] (1) 将(-1,-2)代入函数表达式求解.(2) 将x=-2代入函数表达式求出点P的纵坐标,通过配方可得当yP取最小值时m的值,再将抛物线对应的函数表达式化为顶点式求解.(3) 分别将点A,B的坐标代入函数表达式求得m的值,然后对m的取值范围讨论,找到符合条件的m的取值范围即可.
解:(1) ∵ 抛物线y=x2-2mx+m2-2经过点(-1,-2),∴ -2=1+2m+m2-2,解得m=-1.∴ 抛物线对应的函数表达式为y=x2+2x-1.
(3) ∵ y=x2-2mx+m2-2=(x-m)2-2,∴ 抛物线的顶点坐标为(m,-2).∴ 抛物线随m值的变化而左右平移.将(0,2)代入y=x2-2mx+m2-2,得2=m2-2,解得m=2或m=-2.将(2,2)代入y=x2-2mx+m2-2,得2=4-4m+m2-2,解得m=0或m=4.∴ 当
-2≤m≤0时,抛物线的对称轴在点A左侧,抛物线与线段AB有交点.当2≤m≤4时,抛物线的对称轴在点A右侧,抛物线与线段AB有交点.
∴ -2≤m≤0或2≤m≤4.
(2) 将x=-2代入y=x2-2mx+m2-2,得yP=m2+4m+2=(m+2)2-2.∴ 当m=-2时,yP取最小值.∴ y=x2+4x+2=(x+2)2-2.∴ 当x<-2时,y随x的增大而减小.∵ x1<x2<-2,∴ y1>y2.
跟踪训练
3. (2023·安庆潜山模拟)已知抛物线y=x2-2ax+a2+2a(a>0).
(1) 若a=1,抛物线的顶点坐标为 (1,2) .
(2) 直线x=m与直线y=2x-2交于点P,与抛物线y=x2-2ax+a2+2a交于点Q.若当m<3时,PQ的长随m的增大而减小,则a的取值范围是 a≥2 .
(1,2)
a≥2
类型4 新定义型问题
典例4 (2023·滁州二模)已知二次函数y=x2-2ax+a2+2a=(x-a)2+2a,其图象的顶点坐标为(a,2a),故不论a取何值时,二次函数图象的顶点都在直线y=2x上,我们称图象的顶点位于同一条直线上且形状相同的二次函数为“同源二次函数”,该条直线对应的函数表达式为“根函数”.
(1) 若二次函数y=x2+2x-3和y=-x2-4x-3是“同源二次函数”,求它们的“根函数”.
(2) 已知二次函数C:y=x2-4mx+4m2-4m+1.
① 求满足二次函数C的所有二次函数的“根函数”.
② 若二次函数C的图象与直线x=-3交于点P,求点P到x轴的距离的最小值,以及此时m的值.
[思路点拨] (1) 利用配方法分别求出两个二次函数图象的顶点坐标,利用“根函数”的定义,求出经过两个顶点的直线对应的函数表达式即可得出结论.(2) ① 利用配方法求出二次函数C:y=x2-4mx+4m2-4m+1的图象的顶点坐标,利用“根函数”的定义,求出顶点所在直线对应的函数表达式即可.② 由题意,得出点P的坐标,利用配方法求得点P纵坐标的最小值即可求解.
解:(1) ∵ y=x2+2x-3=(x+1)2-4,∴ 该二次函数图象的顶点坐标为(-1,-4).∵ y=-x2-4x-3=-(x+2)2+1,∴ 该二次函数图象的顶点坐标为(-2,1).设经过点(-1,-4)和点(-2,1)的直线对应的函数表达式为y=kx+b,∴ 解得∴ y=-5x-9.∴ 它们的“根函数”为y=-5x-9.
(2) ① ∵ y=x2-4mx+4m2-4m+1=(x-2m)2-4m+1,∴ 二次函数C的图象的顶点坐标为(2m,-4m+1).设x=2m,y=-4m+1.联立消去m,得y=-2x+1.∴ 满足二次函数C的所有二次函数的“根函数”为y=-2x+1.
② ∵ 二次函数C的图象与直线x=-3交于点P,∴ y=(-3)2-4m·(-3)+4m2-4m+1=4m2+8m+10.∴ 点P的坐标为(-3,4m2+8m+10).∵ 4m2+8m+10=4(m+1)2+6,∴ 当m=-1时,点P的纵坐标最小,最小为6.∴ 点P到x轴的距离的最小值为6,此时m=-1.
跟踪训练
4. (2023·合肥蜀山二模)若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1) 请写出两个为“同簇二次函数”的函数.
解:(1) 答案不唯一,如y=x2和y=2x2为“同簇二次函数”.
(2) 已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+,其中y1的图象经过点P(1,1),y2与y1为“同簇二次函数”.
① 求m的值及二次函数y2的表达式.
解:(2) ① ∵ 二次函数y1=2x2-4mx+2m2+1的图象经过点P(1,1),∴ 1=2-4m+2m2+1,解得m=1.∴ y1=2x2-4x+3=2(x-1)2+1.∵ y2与y1为“同簇二次函数”,∴ 两个函数图象的顶点坐标均为(1,1).∴ y2=a(x-1)2+1=ax2-2ax+a+1.∴ a+1=.∴ a=.∴ y2=(x-1)2+1=x2-x+.
② 如图,A,C是函数y1的图象上的点,B,D是函数y2的图象上的点,且都在对称轴右侧.若AB∥CD∥x轴,BC⊥AB,直接写出的值.
第4题
解: ② 设点B的坐标为(n,(n-1)2+1)(n>1).
∵ AB∥x轴,∴ 令y1=(n-1)2+1,即2(x-1)2+1=(n-1)2+1,得x=(n-1).∴ 点A的坐标为((n-1)+1,(n-1)2+1).
∵ BC⊥AB,∴ 点C的坐标为(n,2(n-1)2+1).∵ CD∥AB,∴ 令y2=2(n-1)2+1,即(x-1)2+1=2(n-1)2+1,得x=2(n-1)+1.∴ 点D的坐标为(2(n-1)+1,2(n-1)2+1).∴ AB=n-[(n-1)+1]=(n-1),CD=2(n-1)+1-n=(2-1)(n-1).∴ ===2.
第4题
强化练习
练习1 与线段长度、面积有关的问题(含最值)
1. (2023·亳州涡阳二模)如图,经过点A(-1,0)的抛物线y=ax2+bx+c与直线y=mx+n相交于点B,C,并与边长为2的正方形OCDE相交于点C,D.
1
2
3
4
(1) 求抛物线和直线BC对应的函数表达式.
解:(1) ∵ 经过点A(-1,0)的抛物线y=ax2+bx+c与直线y=mx+n相交于点B,C,并与边长为2的正方形OCDE相交于点C,D,∴ 点C(0,2),D(2,2).∴ 解得∴ 抛物线对应的函数表达式为y=-x2+x+2.令y=0,得x1=-1,x2=3.∴ 点B的坐标为(3,0).∵ 点B(3,0),C(0,2)在直线y=mx+n上,
∴ 解得∴ 直线BC对应的函数表达式为y=-x+2
1
2
3
4
解:(2) ① 由题意,得点P.如图,过点P作PQ∥y轴交BC于点Q,连接BP,CP,则点Q.∴ PQ=-t2+t+2-=-t2+2t.∴ △PBC的面积为PQ·|xB-xC|==-t2+3t
(2) 若抛物线在第一象限内有一点P,它的横坐标为t.
① 用含t的式子表示△PBC的面积.
第1题答案
1
2
3
4
② 要使点P到直线BC的距离最远,则△PBC的面积取得最大值.由①,得S△PBC=-t2+3t=-+.
∴ 当t=时,S△PBC最大,此时y=-×+×+2=.∴ 点P的坐标为
② 若点P到直线BC的距离最远,请求出此时点P的坐标.
第1题答案
1
2
3
4
2. (2023·合肥蜀山模拟)如图,抛物线y=ax2+bx-3与x轴正半轴交于点A,与y轴交于点B,且经过点(-2,5),抛物线的对称轴为直线x=1.
(1) 求抛物线对应的函数表达式.
解:(1) 根据题意,得解得∴ 抛物线对应的函数表达式为y=x2-2x-3
1
2
3
4
(2) 若P是抛物线在第四象限内的点,求点P到直线AB距离的最大值.
解:(2) 如图,连接AB,AP,BP,过点P作PQ⊥x轴交AB于点Q.∵ 抛物线对应的函数表达式为y=x2-2x-3,
∴ 易得点A(3,0),B(0,-3).∴ OA=3,OB=3.∴ AB==3.设直线AB对应的函数表达式为y=kx+b.∴ 解得∴ 直线AB对应的函数表达式为y=x-3.设点P(m,m2-2m-3),则点Q(m,m-3).∴ PQ=m-3-(m2-2m-3)=-m2+3m.∴ S△ABP=PQ·|xA-xB|=-(m2-3m)=-+.
∴ 当m=时,△ABP的面积最大,最大值为,此时点P到直线AB的距离最大,最大距离为=
第2题答案
1
2
3
4
(3) 已知点M(-6,3),N(0,3),线段MN以每秒1个单位的速度向右平移,同时抛物线以每秒1个单位的速度向上平移.若t秒后,抛物线与线段MN有两个交点,求t的取值范围.
第2题答案
解:(3) t秒后,点M'(t-6,3),N'(t,3),抛物线对应的函数表达式为y=x2-2x-3+t.若抛物线与线段M'N'有两个交点,则点N'在抛物线上(或右侧),且点M'在抛物线上(或左侧).当点N'恰好在抛物线上时,3=t2-2t-3+t,解得t=3或t=-2(舍去).当点M'恰好在抛物线上时,3=(t-6)2-2(t-6)-3+t,解得t=6或t=7(此时只有一个交点,舍去).∴ t的取值范围是3≤t≤6
1
2
3
4
3. (2023·阜阳临泉二模)如图,抛物线y=-x2+x+4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.
(1) 求A,B,C三点及抛物线顶点的坐标.
解:(1) 将y=0代入y=-x2+x+4,得0=-x2+x+4,解得x1=-1,x2=3.∴ 点A(-1,0),B(3,0).将x=0代入y=-x2+x+4,得y=4.∴ 点C(0,4).∵ y=-x2+x+4=-(x-1)2+,∴ 抛物线顶点的坐标为
第3题
1
2
3
4
(2) D是抛物线上的一个动点,设点D的横坐标为m(0<m<3),连接BD,CD.当△BCD的面积最大时,求m的值.
解:(2) 如图①,过点D作DM∥y轴,交BC于点M.设直线BC对应的函数表达式为y=kx+b.将B(3,0),C(0,4)代入y=kx+b,得解得∴ 直线BC对应的函数表达式为y=-x+4.
∵ 点D在抛物线上,∴ 点D(m,-m2+m+4).
∵ DM∥y轴,∴ 点M.∴ S△BCD=DM·|xB-xC|=[-]=-2+.∴ 当m=时,S△BCD最大
第3题答案
第3题
1
2
3
4
(3) 在y轴上是否存在点P,使得∠PAO=∠ABC?若存在,求出点P的坐标;若不存在,请说明理由.
解:(3) 存在 ∵ 点B(3,0),C(0,4),∴ OB=3,OC=4.∴ BC==5.如图②,作BN平分∠ABC交OC于点N,过点N作EN⊥BC于点E.∵ ON⊥OB,NE⊥BC,BN平分∠ABC,∴ ON=EN.∴ ===.∵ =,∴ =.又∵ CN+ON=OC=4,∴ CN=,ON=.∵ ∠OAP1=∠ABC=∠OBN,∠AOP1=∠BON=90°,∴ △AOP1∽△BON. ∴ =,即=.∴ OP1=.同理,可得OP2=.∴ 在y轴上存在点P,使得∠PAO=∠ABC,点P的坐标为或
第3题答案
第3题
1
2
3
4
4. (2023·阜阳太和二模)如图①,抛物线y=-x2+bx+c的顶点坐标为D,与y轴交于点C,与x轴交于点A,B.
第4题
1
2
3
4
(1) 求抛物线对应的函数表达式.
解:(1) ∵ 抛物线y=-x2+bx+c的顶点坐标为D,
∴ 解得∴ 抛物线对应的函数表达式为y=-x2+x+4
1
2
3
4
(2) 若M为y轴上一点,当BM+DM的值最小时,求点M的坐标.
解:(2) 在y=-x2+x+4中,令y=0,得-x2+x+4=0,解得x1=-2,x2=4.∴ 点A(-2,0),B(4,0).如图①,作点B关于y轴的对称点E(-4,0),连接DE,与y轴交于点M,连接BM,此时BM+DM的值最小.设直线DE对应的函数表达式为y=kx+t.根据题意,得解得∴ 直线DE对应的函数表达式为y=x+.令x=0,得y=.∴ 点M的坐标为
第4题答案
1
2
3
4
(3) 如图②,若P是抛物线在第一象限内的一个动点,求△BCP面积的最大值.
解:(3) ∵ y=-x2+x+4,∴ 点C(0,4).设直线BC对应的函数表达式为y=px+q.根据题意,得解得∴ 直线BC对应的函数表达式为y=-x+4.如图②,过点P作PQ∥y轴,交直线BC于点Q.设点P,0<n<4,则点Q(n,-n+4).∴ PQ=-(-n+4)=-n2+2n.∴ S△BCP=PQ·|xB-xC|=×4=-n2+4n=-(n-2)2+4.
∴ 当n=2时,△BCP面积的最大值为4
第4题
1
2
3
4
练习2 含字母系数的二次函数及新定义型问题
1. (2023·合肥模拟)已知二次函数y=mx2-4m2x-3(m为常数,m>0).
(1) 若点(-2,9)在该二次函数的图象上.
① 求m的值.
解:(1) ① ∵ 点(-2,9)在二次函数y=mx2-4m2x-3的图象上,∴ 9=4m+8m2-3,解得m=1或m=-.∵ m>0,∴ m=1
1
2
3
4
② ∵ m=1,∴ 二次函数的表达式为y=x2-4x-3=(x-2)2-7.∴ 二次函数图象的对称轴为直线x=2,顶点坐标为(2,-7).令y=18,得(x-2)2-7=18,解得x=7或x=-3.∵ 当0≤x≤a时,y的最大值为18,且当x=0时,y=-3,∴ 结合函数图象(图略)可知,a=7
② 当0≤x≤a时,y的最大值为18,求a的值.
1
2
3
4
(2) 若P(xP,yP)是该函数图象上的一点,当0≤xP≤4时,yP≤-3,求m的取值范围.
解:(2) ∵ 二次函数y=mx2-4m2x-3,∴ 其图象的对称轴为直线x=2m>0,与y轴的交点为(0,-3).∴ 点(0,-3)关于对称轴的对称点为(4m,-3).∵ P(xP,yP)是该函数图象上一点,当0≤xP≤4时,yP≤-3,∴ 结合函数图象(图略)可知,4m≥4,解得m≥1.∴ m的取值范围是m≥1
1
2
3
4
2. (2023·滁州南谯一模)已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1) 求直线l对应的函数表达式.
解:(1) ∵ 点A(-3,-3),B(1,-1)在直线l:y=kx+b上,∴ 解得∴ 直线l对应的函数表达式为y=x-
1
2
3
4
(2) 若抛物线C与直线l有交点,求a的取值范围.
解:(2) 联立消去y、整理,得2ax2+3x+1=0.
∵ 抛物线C与直线l有交点,∴ Δ=9-8a≥0,解得a≤.又a≠0,∴ a的取值范围是a≤且a≠0
1
2
3
4
(3) 当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,y的最大值为-4,求m的值.
解:(3) ∵ a=-1,∴ y=-x2+2x-1=-(x-1)2.又∵ a<0,
∴ 抛物线开口向下,对称轴为直线x=1.当y=-4时,-x2+2x-1=-4,解得x=-1或x=3.① 在对称轴左侧,即x<1时,y随x的增大而增大,∴ 当x=m+2=-1时,y的最大值为-4.∴ m=-3.② 在对称轴右侧,即x>1时,y随x的增大而减小,∴ 当x=m=3时,y的最大值为-4.综上所述,m的值为-3或3
1
2
3
4
3. (2023·安庆模拟)在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称P为“和谐点”.例如:(1,1),(0,0),(-,-),…都是“和谐点”.
(1) 判断二次函数y=x2-2的图象上是否存在“和谐点”,若存在,求出其“和谐点”的坐标.
解:(1) 存在“和谐点”.设二次函数y=x2-2图象上的“和谐点”的坐标为(x,x),则x=x2-2,解得x=-1或x=2.∴ “和谐点”的坐标为(-1,-1),(2,2)
1
2
3
4
(2) 若二次函数y=ax2+2x+c(a≠0)的图象上有且只有一个“和谐点”(1,1).
① 求该二次函数的表达式.
解:(2) ① ∵ (1,1)是二次函数y=ax2+2x+c(a≠0)图象上的“和谐点”,∴ 1=a+2+c.∴ c=-a-1.∵ 二次函数y=ax2+2x+c(a≠0)的图象上有且只有一个“和谐点”,∴ ax2+2x+c=x,即关于x的一元二次方程ax2+x+c=0有两个相等的实数根.∴ Δ=1-4ac=0.联立解得∴ 该二次函数的表达式为y=-x2+2x-
1
2
3
4
② 由①可知,y=-x2+2x+1=-(x-2)2+3,∴ 二次函数图象的对称轴为直线x=2.当x=2时,y=3;当x=0时,y=1;当x=4时,y=1.∵ 当0≤x≤m时,函数的最小值为1,最大值为3,∴ 结合图象(图略)可知,m的取值范围是2≤m≤4
② 当0≤x≤m时,函数y=ax2+2x+c+(a≠0)的最小值为1,最大值为3,求实数m的取值范围.
1
2
3
4
4. (2023·长沙)我们约定:若关于x的二次函数y1=a1x2+b1x+c1与y2=a2x2+b2x+c2同时满足+(b2+b1)2+|c2-a1|=0,(b1-b2)2023≠0,则称函数y1与函数y2互为“美美与共”函数.
(1) 若关于x的二次函数y1=2x2+kx+3与y2=mx2+x+n互为“美美与共”函数,求k,m,n的值.
解:(1) 由题意可知,a2=c1,a1=c2,b1=-b2≠0.∴ k=-1,m=3,n=2
1
2
3
4
(2) 对于任意非零实数r,s,点P(r,t)与点Q(s,t)(r≠s)始终在关于x的函数y1=x2+2rx+s的图象上运动,函数y2与y1互为“美美与共”函数.
① 求函数y2的图象的对称轴.
解:(2) ① ∵ 点P(r,t)与点Q(s,t)(r≠s)始终在关于x的函数y1=x2+2rx+s的图象上运动,∴ =-=-r,即s=-3r.∵ 函数y2与y1互为“美美与共”函数,∴ y2=sx2-2rx+1.∴ 函数y2的图象的对称轴为直线x=-==-
1
2
3
4
② 函数y2的图象是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由.
解:(2) ② 函数y2的图象经过定点(0,1), 由①知,y2=-3rx2-2rx+1=-(3x2+2x)r+1.令3x2+2x=0,解得x1=0,x2=-.∴ 函数y2的图象经过定点(0,1),
1
2
3
4
专题四 二次函数综合题
类型1 与线段有关的问题(含最值)
典例1 如图①,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(-4,0),C(1,0)两点,与y轴交于点A(0,-4).
典例1图
(1) 求该抛物线对应的函数表达式.
(2) 如图②,作直线AB,P是直线AB下方抛物线上的动点,过点P作y轴的平行线交AB于点E,过点P作PD⊥AB于点D.求PD+PE的最大值及此时点P的坐标.
(3) 在(2)中PD+PE取得最大值的条件下,将该抛物线向左平移2个单位,P'为点P的对应点,平移后的抛物线与y轴交于点A',M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点P',A',M,N为顶点的四边形是平行四边形,直接写出所有符合条件的点N的坐标.
[思路点拨] (1) 将A(0,-4),B(-4,0),C(1,0)代入y=ax2+bx+c即可建立方程组求解.(2) 先求出直线AB对应的函数表达式,设点P的坐标为(t,t2+3t-4),则点E的坐标为(t,-t-4).建立PD+PE与t之间的函数表达式即可求解.(3) 根据平移确定新抛物线对应的函数表达式,进而可求出点A'的坐标,以平行四边形的对角线为切入点,根据“平行四边形的对角线互相平分”即可求解.
解:(1) 根据题意,得抛物线y=ax2+bx+c经过点A(0,-4),B(-4,0),C(1,0),∴ 该抛物线对应的函数表达式为y=x2+3x-4.
典例1图
(2) 设直线AB对应的函数表达式为y=kx+b1.∵ 点A(0,-4),B(-4,0)在直线AB上,∴ 解得∴ 直线AB对应的函数表达式为y=-x-4.∵ PE∥y 轴,且PD⊥AB,∴ 易得∠DPE=∠ABC.∴ PD=PE·cos∠DPE=PE·cos∠ABC.∵ OA=OB=4,∠AOB=90°,∴ ∠ABC=45°.∴ PD=PE.∴ PD+PE=PE+PE=PE.
设点P的坐标为(t,t2+3t-4),-4<t<0,则点E的坐标为(t,-t-4).∴ PE=-t-4-t2-3t+4=-t2-4t=-(t+2)2+4.∴ 当t=-2时,PE的长取得最大值4,此时PE取得最大值2+4,点P的坐标为(-2,-6).∴ PD+PE的最大值为4+2,此时点P的坐标为(-2,-6).
(3) ∵ 将抛物线y=x2+3x-4向左平移2个单位得抛物线y=(x+2)2+3(x+2)-4=x2+7x+6,∴ 新抛物线的对称轴是直线x=-=-.在y=x2+7x+6中,令x=0,得y=6.∴ 点A'的坐标为(0,6).将点P(-2,-6)向左平移2个单位得点P'(-4,-6).设点M,N(r,r2+7r+6).分三种情况讨论:
① 当A'P', MN为对角线时,A'P',MN 的中点重合,∴ 解得r=-.∴ 点N的坐标为.② 当A'M,P'N为对角线时,A'M,P'N的中点重合,∴ 解得r=.∴ 点N的坐标为.
③ 当A'N,P'M为对角线时,A'N,P'M的中点重合,解得r=-.∴ 点N的坐标为.综上所述,符合条件的点N的坐标为或或.
跟踪训练
1. (2023·合肥庐江二模)如图,直线m:y=b和直线n:y=x-b分别与y轴交于点A,B,顶点为C的抛物线L:y=-x2+bx与x轴的右交点为D.
(1) 若AB=8,求b的值和抛物线L的对称轴.
解:(1) 在y=x-b中,令x=0,得y=-b.∴ 点B(0,-b).∵ AB=8,点A(0,b),∴ b-(-b)=8,解得b=4.∴ 抛物线L对应的函数表达式为y=-x2+4x=-(x-2)2+4.∴ 抛物线L的对称轴为直线x=2.
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(2) 当顶点C在直线m下方时,求顶点C到直线m的距离的最大值.
解:解:(2) ∵ y=-x2+bx=-+,∴ 抛物线L的顶点C的坐标为.∵ 点C在直线m下方,
∴ 点C到直线m的距离为b-=-(b-2)2+1.∵ -<0,∴ 当b=2时,b-取得最大值1.∴ 顶点C到直线m距离的最大值为1.
第1题
(3) 在抛物线L和直线n所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“整点”.当b=2023时,求“整点”的个数.
解:解:(3) 当b=2023时,抛物线L对应的函数表达式为y=-x2+2023x,直线n对应的函数表达式为y=x-2023.令-x2+2023x=x-2023,即x2-2022x-2023=0,解得x1=-1,x2=2023.∵ 对y=-x2+2023x和y=x-2023,每一个整数x的值都对应一个整数y的值,且-1和2023之间(不包括-1和2023)共有2023个整数,∴ “整点”的个数为2023×2+2=4048.
第1题
类型2 与面积有关的问题(含最值)
典例2 (2023·芜湖一模)如图,抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-1,0),直线y=kx+3经过点B,C.
典例2图
(1) 抛物线对应的函数表达式为 y=-x2+2x+3 ,直线BC对应的函数表达式为 y=-x+3 .
(2) D是第一象限内抛物线上的一个动点,过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD.设点D的横坐标为m,△BCD的面积为S,求S关于m的函数表达式及自变量m的取值范围,并求出S的最大值.
(3) 已知M为抛物线对称轴上的一个动点,若△MBC是以BC为直角边的直角三角形,请直接写出点M的坐标.
y=-x2+2x+3
y=-x+3
[思路点拨] (1) 根据直线y=kx+3经过点C,点C在y轴上,可求得点C的坐标,从而得到c的值,将点A的坐标代入抛物线对应的函数表达式即可求解.再求出点B的坐标,从而求得直线BC对应的函数表达式.(2) 根据题意,可得点D(m,-m2+2m+3),E(m,-m+3),则DE=-m2+3m.再由S△BCD=DE·OB求出S关于m的函数表达式,由二次函数的性质即可求出S的最大值.(3) 分MC是斜边、MB是斜边两种情况,分别求解即可.
解:(2) 由题意可知,点D(m,-m2+2m+3),E(m,-m+3).∴ DE=(-m2+2m+3)-(-m+3)=-m2+3m.由B(3,0)可知,OB=3.∵ S△BCD=DE·OB,∴ S=(-m2+3m)=-m2+m=
-+(0<m<3).∵ -<0,∴ 当m=时,S有最大值,最大值为.∴ S关于m的函数表达式为S=-m2+m(0<m<3),S的最大值为.
典例2图
(3) 抛物线y=-x2+2x+3的对称轴为直线x=1.根据题意,设点M(1,a),则MB2=a2+4,MC2=1+(a-3)2,BC2=18.① 当MC是斜边时,MC2=MB2+BC2,即1+(a-3)2=a2+4+18,解得a=-2.∴ 点M(1,-2).② 当MB是斜边时,MB2=MC2+BC2,即a2+4=1+(a-3)2+18,解得a=4.∴ 点M(1,4).综上所述,点M的坐标为(1,-2)或(1,4).
典例2图
跟踪训练
2. (2023·滁州来安二模)如图①,一块钢板截面的一边为线段AB,另一边曲线ACB为抛物线的一部分,现沿线段BC将这块钢板分成甲、乙两部分,以边AB所在直线为x轴,经过点C且与AB垂直的直线为y轴,建立平面直角坐标系,O为原点.已知OA=2米,OB=8米,OC=6米.
第2题
(1) 求曲线ACB所在抛物线对应的函数表达式(不用写出自变量的取值范围).
解:(1) ∵ OC=6米,∴ 可设曲线ACB所在抛物线对应的函数表达式为y=ax2+bx+6.∵ OA=2米,OB=8米,∴ 点A的坐标为(-2,0),点B的坐标为(8,0).∵ 点A,B在曲线ACB所在的抛物线上,
∴ 解得∴ 曲线ACB所在抛物线对应的函数表达式为y=-x2+x+6.
(2) 如图②,在这块钢板的甲部分中截取一个矩形DEFG,其中D为BC的中点,点E,F均在线段AB上,点G在曲线AC上.求EF的长.
解:(2) ∵ 点B(8,0),C(0,6),D为BC的中点,∴ 点D的坐标为(4,3).∴ 点E的坐标为(4,0).当y=3时,-x2+x+6=3,解得x1=3+,x2=3-.∴ 结合题图可知,点G的横坐标为3-.∵ 四边形DEFG是矩形,∴ DE⊥x轴,GF⊥x轴.∴ 点F的坐标为(3-,0).∴ EF=4-(3-)=(+1)米.
(3) 如图③,在这块钢板的乙部分中截取一个△PBC,其中点P在曲线BC上,记△PBC的面积为S平方米.求S的最大值.
解:(3) 设直线BC对应的函数表达式为y=kx+c(k≠0).∵ 点B(8,0),C(0,6)在直线BC上,∴ 解得
∴ 直线BC对应的函数表达式为y=-x+6.
∵ 点P在抛物线上,∴ 设点P的坐标为,0<m<8.如图③,过点P作PH⊥x轴于点H,交BC于点Q,则PH∥y轴,点Q的坐标为(m,-m+6).∴ QP=-m2+m+6-(-m+6)=-m2+3m.∵ S△PBC=S△CPQ+S△BPQ=QP·OB,∴ S=·8=
-m2+12m=-(m-4)2+24.∵ -<0,0<m<8,∴ 当m=4时,S取得最大值,最大值为24.
类型3 含字母系数的二次函数问题
典例3 (2023·芜湖南陵模拟)已知抛物线y=x2-2mx+m2-2与直线x=-2交于点P.
(1) 当抛物线经过点(-1,-2)时,求抛物线对应的函数表达式.
(2) 设点P的纵坐标为yP,当yP取最小值时,抛物线上有两点(x1,y1),(x2,y2),x1<x2<-2,比较y1与y2的大小.
(3) 若线段AB的两个端点分别是A(0,2),B(2,2),当抛物线与线段AB有公共点时,求出m的取值范围.
[思路点拨] (1) 将(-1,-2)代入函数表达式求解.(2) 将x=-2代入函数表达式求出点P的纵坐标,通过配方可得当yP取最小值时m的值,再将抛物线对应的函数表达式化为顶点式求解.(3) 分别将点A,B的坐标代入函数表达式求得m的值,然后对m的取值范围讨论,找到符合条件的m的取值范围即可.
解:(1) ∵ 抛物线y=x2-2mx+m2-2经过点(-1,-2),∴ -2=1+2m+m2-2,解得m=-1.∴ 抛物线对应的函数表达式为y=x2+2x-1.
(3) ∵ y=x2-2mx+m2-2=(x-m)2-2,∴ 抛物线的顶点坐标为(m,-2).∴ 抛物线随m值的变化而左右平移.将(0,2)代入y=x2-2mx+m2-2,得2=m2-2,解得m=2或m=-2.将(2,2)代入y=x2-2mx+m2-2,得2=4-4m+m2-2,解得m=0或m=4.∴ 当
-2≤m≤0时,抛物线的对称轴在点A左侧,抛物线与线段AB有交点.当2≤m≤4时,抛物线的对称轴在点A右侧,抛物线与线段AB有交点.
∴ -2≤m≤0或2≤m≤4.
(2) 将x=-2代入y=x2-2mx+m2-2,得yP=m2+4m+2=(m+2)2-2.∴ 当m=-2时,yP取最小值.∴ y=x2+4x+2=(x+2)2-2.∴ 当x<-2时,y随x的增大而减小.∵ x1<x2<-2,∴ y1>y2.
跟踪训练
3. (2023·安庆潜山模拟)已知抛物线y=x2-2ax+a2+2a(a>0).
(1) 若a=1,抛物线的顶点坐标为 (1,2) .
(2) 直线x=m与直线y=2x-2交于点P,与抛物线y=x2-2ax+a2+2a交于点Q.若当m<3时,PQ的长随m的增大而减小,则a的取值范围是 a≥2 .
(1,2)
a≥2
类型4 新定义型问题
典例4 (2023·滁州二模)已知二次函数y=x2-2ax+a2+2a=(x-a)2+2a,其图象的顶点坐标为(a,2a),故不论a取何值时,二次函数图象的顶点都在直线y=2x上,我们称图象的顶点位于同一条直线上且形状相同的二次函数为“同源二次函数”,该条直线对应的函数表达式为“根函数”.
(1) 若二次函数y=x2+2x-3和y=-x2-4x-3是“同源二次函数”,求它们的“根函数”.
(2) 已知二次函数C:y=x2-4mx+4m2-4m+1.
① 求满足二次函数C的所有二次函数的“根函数”.
② 若二次函数C的图象与直线x=-3交于点P,求点P到x轴的距离的最小值,以及此时m的值.
[思路点拨] (1) 利用配方法分别求出两个二次函数图象的顶点坐标,利用“根函数”的定义,求出经过两个顶点的直线对应的函数表达式即可得出结论.(2) ① 利用配方法求出二次函数C:y=x2-4mx+4m2-4m+1的图象的顶点坐标,利用“根函数”的定义,求出顶点所在直线对应的函数表达式即可.② 由题意,得出点P的坐标,利用配方法求得点P纵坐标的最小值即可求解.
解:(1) ∵ y=x2+2x-3=(x+1)2-4,∴ 该二次函数图象的顶点坐标为(-1,-4).∵ y=-x2-4x-3=-(x+2)2+1,∴ 该二次函数图象的顶点坐标为(-2,1).设经过点(-1,-4)和点(-2,1)的直线对应的函数表达式为y=kx+b,∴ 解得∴ y=-5x-9.∴ 它们的“根函数”为y=-5x-9.
(2) ① ∵ y=x2-4mx+4m2-4m+1=(x-2m)2-4m+1,∴ 二次函数C的图象的顶点坐标为(2m,-4m+1).设x=2m,y=-4m+1.联立消去m,得y=-2x+1.∴ 满足二次函数C的所有二次函数的“根函数”为y=-2x+1.
② ∵ 二次函数C的图象与直线x=-3交于点P,∴ y=(-3)2-4m·(-3)+4m2-4m+1=4m2+8m+10.∴ 点P的坐标为(-3,4m2+8m+10).∵ 4m2+8m+10=4(m+1)2+6,∴ 当m=-1时,点P的纵坐标最小,最小为6.∴ 点P到x轴的距离的最小值为6,此时m=-1.
跟踪训练
4. (2023·合肥蜀山二模)若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1) 请写出两个为“同簇二次函数”的函数.
解:(1) 答案不唯一,如y=x2和y=2x2为“同簇二次函数”.
(2) 已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+,其中y1的图象经过点P(1,1),y2与y1为“同簇二次函数”.
① 求m的值及二次函数y2的表达式.
解:(2) ① ∵ 二次函数y1=2x2-4mx+2m2+1的图象经过点P(1,1),∴ 1=2-4m+2m2+1,解得m=1.∴ y1=2x2-4x+3=2(x-1)2+1.∵ y2与y1为“同簇二次函数”,∴ 两个函数图象的顶点坐标均为(1,1).∴ y2=a(x-1)2+1=ax2-2ax+a+1.∴ a+1=.∴ a=.∴ y2=(x-1)2+1=x2-x+.
② 如图,A,C是函数y1的图象上的点,B,D是函数y2的图象上的点,且都在对称轴右侧.若AB∥CD∥x轴,BC⊥AB,直接写出的值.
第4题
解: ② 设点B的坐标为(n,(n-1)2+1)(n>1).
∵ AB∥x轴,∴ 令y1=(n-1)2+1,即2(x-1)2+1=(n-1)2+1,得x=(n-1).∴ 点A的坐标为((n-1)+1,(n-1)2+1).
∵ BC⊥AB,∴ 点C的坐标为(n,2(n-1)2+1).∵ CD∥AB,∴ 令y2=2(n-1)2+1,即(x-1)2+1=2(n-1)2+1,得x=2(n-1)+1.∴ 点D的坐标为(2(n-1)+1,2(n-1)2+1).∴ AB=n-[(n-1)+1]=(n-1),CD=2(n-1)+1-n=(2-1)(n-1).∴ ===2.
第4题
强化练习
练习1 与线段长度、面积有关的问题(含最值)
1. (2023·亳州涡阳二模)如图,经过点A(-1,0)的抛物线y=ax2+bx+c与直线y=mx+n相交于点B,C,并与边长为2的正方形OCDE相交于点C,D.
1
2
3
4
(1) 求抛物线和直线BC对应的函数表达式.
解:(1) ∵ 经过点A(-1,0)的抛物线y=ax2+bx+c与直线y=mx+n相交于点B,C,并与边长为2的正方形OCDE相交于点C,D,∴ 点C(0,2),D(2,2).∴ 解得∴ 抛物线对应的函数表达式为y=-x2+x+2.令y=0,得x1=-1,x2=3.∴ 点B的坐标为(3,0).∵ 点B(3,0),C(0,2)在直线y=mx+n上,
∴ 解得∴ 直线BC对应的函数表达式为y=-x+2
1
2
3
4
解:(2) ① 由题意,得点P.如图,过点P作PQ∥y轴交BC于点Q,连接BP,CP,则点Q.∴ PQ=-t2+t+2-=-t2+2t.∴ △PBC的面积为PQ·|xB-xC|==-t2+3t
(2) 若抛物线在第一象限内有一点P,它的横坐标为t.
① 用含t的式子表示△PBC的面积.
第1题答案
1
2
3
4
② 要使点P到直线BC的距离最远,则△PBC的面积取得最大值.由①,得S△PBC=-t2+3t=-+.
∴ 当t=时,S△PBC最大,此时y=-×+×+2=.∴ 点P的坐标为
② 若点P到直线BC的距离最远,请求出此时点P的坐标.
第1题答案
1
2
3
4
2. (2023·合肥蜀山模拟)如图,抛物线y=ax2+bx-3与x轴正半轴交于点A,与y轴交于点B,且经过点(-2,5),抛物线的对称轴为直线x=1.
(1) 求抛物线对应的函数表达式.
解:(1) 根据题意,得解得∴ 抛物线对应的函数表达式为y=x2-2x-3
1
2
3
4
(2) 若P是抛物线在第四象限内的点,求点P到直线AB距离的最大值.
解:(2) 如图,连接AB,AP,BP,过点P作PQ⊥x轴交AB于点Q.∵ 抛物线对应的函数表达式为y=x2-2x-3,
∴ 易得点A(3,0),B(0,-3).∴ OA=3,OB=3.∴ AB==3.设直线AB对应的函数表达式为y=kx+b.∴ 解得∴ 直线AB对应的函数表达式为y=x-3.设点P(m,m2-2m-3),则点Q(m,m-3).∴ PQ=m-3-(m2-2m-3)=-m2+3m.∴ S△ABP=PQ·|xA-xB|=-(m2-3m)=-+.
∴ 当m=时,△ABP的面积最大,最大值为,此时点P到直线AB的距离最大,最大距离为=
第2题答案
1
2
3
4
(3) 已知点M(-6,3),N(0,3),线段MN以每秒1个单位的速度向右平移,同时抛物线以每秒1个单位的速度向上平移.若t秒后,抛物线与线段MN有两个交点,求t的取值范围.
第2题答案
解:(3) t秒后,点M'(t-6,3),N'(t,3),抛物线对应的函数表达式为y=x2-2x-3+t.若抛物线与线段M'N'有两个交点,则点N'在抛物线上(或右侧),且点M'在抛物线上(或左侧).当点N'恰好在抛物线上时,3=t2-2t-3+t,解得t=3或t=-2(舍去).当点M'恰好在抛物线上时,3=(t-6)2-2(t-6)-3+t,解得t=6或t=7(此时只有一个交点,舍去).∴ t的取值范围是3≤t≤6
1
2
3
4
3. (2023·阜阳临泉二模)如图,抛物线y=-x2+x+4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.
(1) 求A,B,C三点及抛物线顶点的坐标.
解:(1) 将y=0代入y=-x2+x+4,得0=-x2+x+4,解得x1=-1,x2=3.∴ 点A(-1,0),B(3,0).将x=0代入y=-x2+x+4,得y=4.∴ 点C(0,4).∵ y=-x2+x+4=-(x-1)2+,∴ 抛物线顶点的坐标为
第3题
1
2
3
4
(2) D是抛物线上的一个动点,设点D的横坐标为m(0<m<3),连接BD,CD.当△BCD的面积最大时,求m的值.
解:(2) 如图①,过点D作DM∥y轴,交BC于点M.设直线BC对应的函数表达式为y=kx+b.将B(3,0),C(0,4)代入y=kx+b,得解得∴ 直线BC对应的函数表达式为y=-x+4.
∵ 点D在抛物线上,∴ 点D(m,-m2+m+4).
∵ DM∥y轴,∴ 点M.∴ S△BCD=DM·|xB-xC|=[-]=-2+.∴ 当m=时,S△BCD最大
第3题答案
第3题
1
2
3
4
(3) 在y轴上是否存在点P,使得∠PAO=∠ABC?若存在,求出点P的坐标;若不存在,请说明理由.
解:(3) 存在 ∵ 点B(3,0),C(0,4),∴ OB=3,OC=4.∴ BC==5.如图②,作BN平分∠ABC交OC于点N,过点N作EN⊥BC于点E.∵ ON⊥OB,NE⊥BC,BN平分∠ABC,∴ ON=EN.∴ ===.∵ =,∴ =.又∵ CN+ON=OC=4,∴ CN=,ON=.∵ ∠OAP1=∠ABC=∠OBN,∠AOP1=∠BON=90°,∴ △AOP1∽△BON. ∴ =,即=.∴ OP1=.同理,可得OP2=.∴ 在y轴上存在点P,使得∠PAO=∠ABC,点P的坐标为或
第3题答案
第3题
1
2
3
4
4. (2023·阜阳太和二模)如图①,抛物线y=-x2+bx+c的顶点坐标为D,与y轴交于点C,与x轴交于点A,B.
第4题
1
2
3
4
(1) 求抛物线对应的函数表达式.
解:(1) ∵ 抛物线y=-x2+bx+c的顶点坐标为D,
∴ 解得∴ 抛物线对应的函数表达式为y=-x2+x+4
1
2
3
4
(2) 若M为y轴上一点,当BM+DM的值最小时,求点M的坐标.
解:(2) 在y=-x2+x+4中,令y=0,得-x2+x+4=0,解得x1=-2,x2=4.∴ 点A(-2,0),B(4,0).如图①,作点B关于y轴的对称点E(-4,0),连接DE,与y轴交于点M,连接BM,此时BM+DM的值最小.设直线DE对应的函数表达式为y=kx+t.根据题意,得解得∴ 直线DE对应的函数表达式为y=x+.令x=0,得y=.∴ 点M的坐标为
第4题答案
1
2
3
4
(3) 如图②,若P是抛物线在第一象限内的一个动点,求△BCP面积的最大值.
解:(3) ∵ y=-x2+x+4,∴ 点C(0,4).设直线BC对应的函数表达式为y=px+q.根据题意,得解得∴ 直线BC对应的函数表达式为y=-x+4.如图②,过点P作PQ∥y轴,交直线BC于点Q.设点P,0<n<4,则点Q(n,-n+4).∴ PQ=-(-n+4)=-n2+2n.∴ S△BCP=PQ·|xB-xC|=×4=-n2+4n=-(n-2)2+4.
∴ 当n=2时,△BCP面积的最大值为4
第4题
1
2
3
4
练习2 含字母系数的二次函数及新定义型问题
1. (2023·合肥模拟)已知二次函数y=mx2-4m2x-3(m为常数,m>0).
(1) 若点(-2,9)在该二次函数的图象上.
① 求m的值.
解:(1) ① ∵ 点(-2,9)在二次函数y=mx2-4m2x-3的图象上,∴ 9=4m+8m2-3,解得m=1或m=-.∵ m>0,∴ m=1
1
2
3
4
② ∵ m=1,∴ 二次函数的表达式为y=x2-4x-3=(x-2)2-7.∴ 二次函数图象的对称轴为直线x=2,顶点坐标为(2,-7).令y=18,得(x-2)2-7=18,解得x=7或x=-3.∵ 当0≤x≤a时,y的最大值为18,且当x=0时,y=-3,∴ 结合函数图象(图略)可知,a=7
② 当0≤x≤a时,y的最大值为18,求a的值.
1
2
3
4
(2) 若P(xP,yP)是该函数图象上的一点,当0≤xP≤4时,yP≤-3,求m的取值范围.
解:(2) ∵ 二次函数y=mx2-4m2x-3,∴ 其图象的对称轴为直线x=2m>0,与y轴的交点为(0,-3).∴ 点(0,-3)关于对称轴的对称点为(4m,-3).∵ P(xP,yP)是该函数图象上一点,当0≤xP≤4时,yP≤-3,∴ 结合函数图象(图略)可知,4m≥4,解得m≥1.∴ m的取值范围是m≥1
1
2
3
4
2. (2023·滁州南谯一模)已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1) 求直线l对应的函数表达式.
解:(1) ∵ 点A(-3,-3),B(1,-1)在直线l:y=kx+b上,∴ 解得∴ 直线l对应的函数表达式为y=x-
1
2
3
4
(2) 若抛物线C与直线l有交点,求a的取值范围.
解:(2) 联立消去y、整理,得2ax2+3x+1=0.
∵ 抛物线C与直线l有交点,∴ Δ=9-8a≥0,解得a≤.又a≠0,∴ a的取值范围是a≤且a≠0
1
2
3
4
(3) 当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,y的最大值为-4,求m的值.
解:(3) ∵ a=-1,∴ y=-x2+2x-1=-(x-1)2.又∵ a<0,
∴ 抛物线开口向下,对称轴为直线x=1.当y=-4时,-x2+2x-1=-4,解得x=-1或x=3.① 在对称轴左侧,即x<1时,y随x的增大而增大,∴ 当x=m+2=-1时,y的最大值为-4.∴ m=-3.② 在对称轴右侧,即x>1时,y随x的增大而减小,∴ 当x=m=3时,y的最大值为-4.综上所述,m的值为-3或3
1
2
3
4
3. (2023·安庆模拟)在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称P为“和谐点”.例如:(1,1),(0,0),(-,-),…都是“和谐点”.
(1) 判断二次函数y=x2-2的图象上是否存在“和谐点”,若存在,求出其“和谐点”的坐标.
解:(1) 存在“和谐点”.设二次函数y=x2-2图象上的“和谐点”的坐标为(x,x),则x=x2-2,解得x=-1或x=2.∴ “和谐点”的坐标为(-1,-1),(2,2)
1
2
3
4
(2) 若二次函数y=ax2+2x+c(a≠0)的图象上有且只有一个“和谐点”(1,1).
① 求该二次函数的表达式.
解:(2) ① ∵ (1,1)是二次函数y=ax2+2x+c(a≠0)图象上的“和谐点”,∴ 1=a+2+c.∴ c=-a-1.∵ 二次函数y=ax2+2x+c(a≠0)的图象上有且只有一个“和谐点”,∴ ax2+2x+c=x,即关于x的一元二次方程ax2+x+c=0有两个相等的实数根.∴ Δ=1-4ac=0.联立解得∴ 该二次函数的表达式为y=-x2+2x-
1
2
3
4
② 由①可知,y=-x2+2x+1=-(x-2)2+3,∴ 二次函数图象的对称轴为直线x=2.当x=2时,y=3;当x=0时,y=1;当x=4时,y=1.∵ 当0≤x≤m时,函数的最小值为1,最大值为3,∴ 结合图象(图略)可知,m的取值范围是2≤m≤4
② 当0≤x≤m时,函数y=ax2+2x+c+(a≠0)的最小值为1,最大值为3,求实数m的取值范围.
1
2
3
4
4. (2023·长沙)我们约定:若关于x的二次函数y1=a1x2+b1x+c1与y2=a2x2+b2x+c2同时满足+(b2+b1)2+|c2-a1|=0,(b1-b2)2023≠0,则称函数y1与函数y2互为“美美与共”函数.
(1) 若关于x的二次函数y1=2x2+kx+3与y2=mx2+x+n互为“美美与共”函数,求k,m,n的值.
解:(1) 由题意可知,a2=c1,a1=c2,b1=-b2≠0.∴ k=-1,m=3,n=2
1
2
3
4
(2) 对于任意非零实数r,s,点P(r,t)与点Q(s,t)(r≠s)始终在关于x的函数y1=x2+2rx+s的图象上运动,函数y2与y1互为“美美与共”函数.
① 求函数y2的图象的对称轴.
解:(2) ① ∵ 点P(r,t)与点Q(s,t)(r≠s)始终在关于x的函数y1=x2+2rx+s的图象上运动,∴ =-=-r,即s=-3r.∵ 函数y2与y1互为“美美与共”函数,∴ y2=sx2-2rx+1.∴ 函数y2的图象的对称轴为直线x=-==-
1
2
3
4
② 函数y2的图象是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由.
解:(2) ② 函数y2的图象经过定点(0,1), 由①知,y2=-3rx2-2rx+1=-(3x2+2x)r+1.令3x2+2x=0,解得x1=0,x2=-.∴ 函数y2的图象经过定点(0,1),
1
2
3
4
同课章节目录
