2024年中考数学二轮复习突破课件:专题五 几何探究题(共69张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习突破课件:专题五 几何探究题(共69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:38:58 | ||
图片预览







文档简介
(共69张PPT)
专题五 几何探究题
类型1 利用截长补短法构造线段的和与差
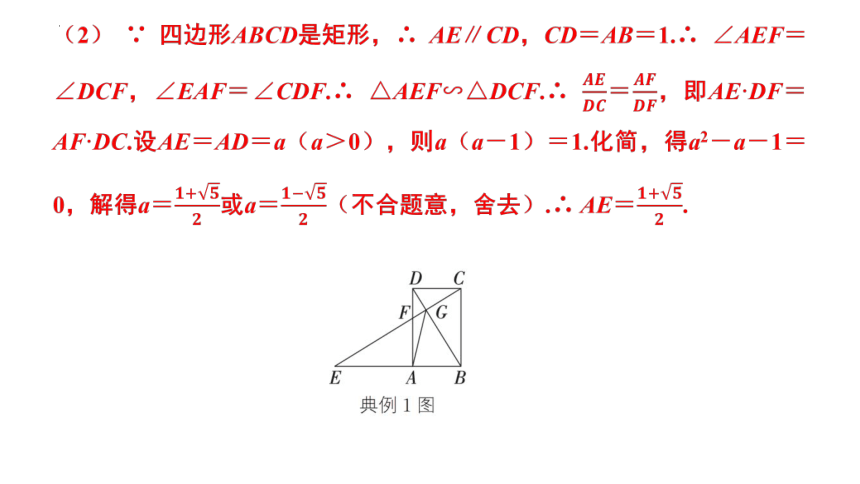
典例1 如图,四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.
(1) 求证:BD⊥EC.
(2) 若AB=1,求AE的长.
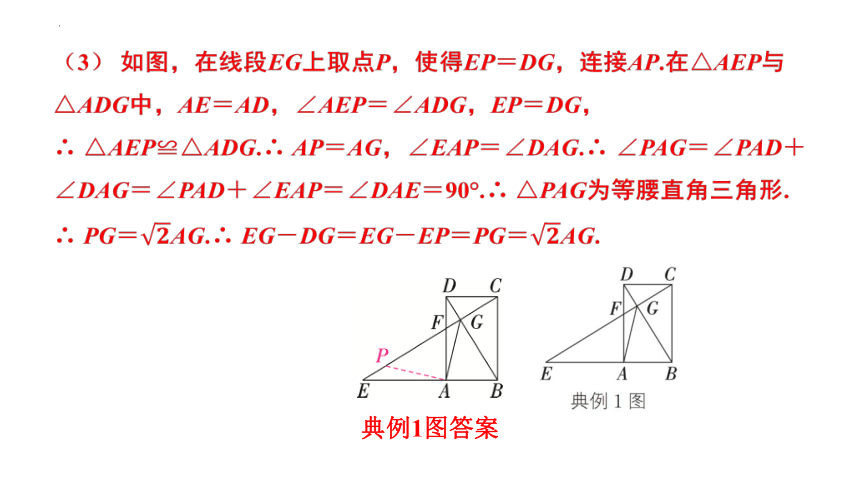
(3) 连接AG.求证:EG-DG=AG.
[思路点拨] (1) 证明△AEF≌△ADB,得出∠AEF=∠ADB,证得∠EGB=90°,可得出结论.(2) 证明△AEF∽△DCF,得出=,即AE·DF=AF·DC.设AE=AD=a(a>0),则有a(a-1)=1,解方程即可得出答案.(3) 在线段EG上取点P,使得EP=DG,连接AP,证明△AEP≌△ADG,得出AP=AG,∠EAP=∠DAG,证得△PAG为等腰直角三角形,即可得出结论.
解:(1) ∵ 四边形ABCD是矩形,点E在BA的延长线上,∴ ∠EAF=∠DAB=90°.又∵ AE=AD,AF=AB,∴ △AEF≌△ADB.∴ ∠AEF=∠ADB.∴ ∠GEB+∠GBE=∠ADB+∠ABD=90°.∴ ∠EGB=90°.
∴ BD⊥EC.
(2) ∵ 四边形ABCD是矩形,∴ AE∥CD,CD=AB=1.∴ ∠AEF=∠DCF,∠EAF=∠CDF.∴ △AEF∽△DCF.∴ =,即AE·DF=AF·DC.设AE=AD=a(a>0),则a(a-1)=1.化简,得a2-a-1=0,解得a=或a=(不合题意,舍去).∴ AE=.
(3) 如图,在线段EG上取点P,使得EP=DG,连接AP.在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴ △AEP≌△ADG.∴ AP=AG,∠EAP=∠DAG.∴ ∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°.∴ △PAG为等腰直角三角形.
∴ PG=AG.∴ EG-DG=EG-EP=PG=AG.
典例1图答案
跟踪训练
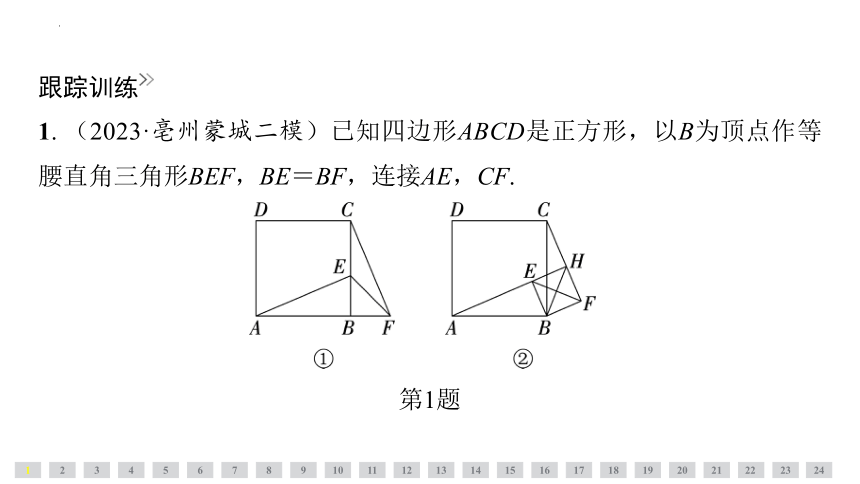
1. (2023·亳州蒙城二模)已知四边形ABCD是正方形,以B为顶点作等腰直角三角形BEF,BE=BF,连接AE,CF.
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
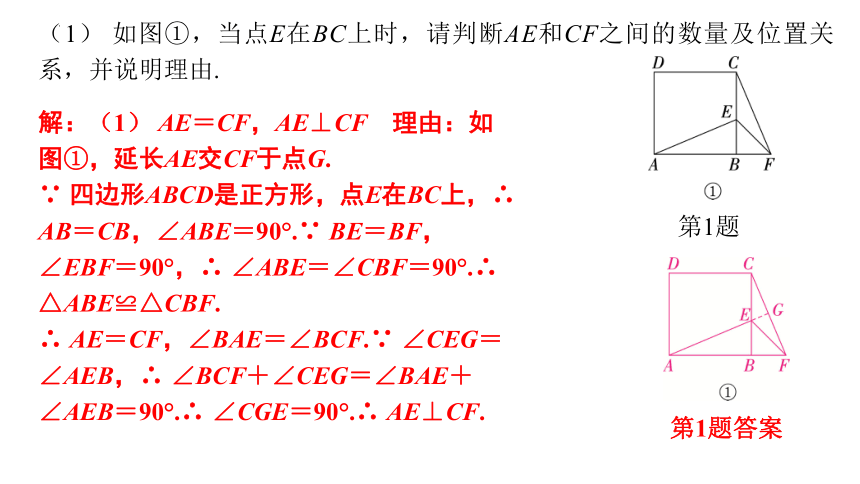
(1) 如图①,当点E在BC上时,请判断AE和CF之间的数量及位置关系,并说明理由.
解:(1) AE=CF,AE⊥CF 理由:如图①,延长AE交CF于点G.
∵ 四边形ABCD是正方形,点E在BC上,∴ AB=CB,∠ABE=90°.∵ BE=BF,∠EBF=90°,∴ ∠ABE=∠CBF=90°.∴ △ABE≌△CBF.
∴ AE=CF,∠BAE=∠BCF.∵ ∠CEG=∠AEB,∴ ∠BCF+∠CEG=∠BAE+∠AEB=90°.∴ ∠CGE=90°.∴ AE⊥CF.
第1题答案
第1题
(2) 如图②,H是AE的延长线与直线CF的交点,连接BH,将△BEF绕点B旋转.当点F在直线BC的右侧时,求证:AH-CH=BH.
解:(2) 如图②,在AH上取点L,使得AL=CH,连接BL.∵ AB=CB,∠ABE=∠CBF=90°-∠CBE,BE=BF,∴ △ABE≌△CBF.
∴ ∠BAE=∠BCF,即∠BAL=∠BCH.又∵ AB=CB,AL=CH,
∴ △BAL≌△BCH.∴ BL=BH,∠ABL=∠CBH.∴ ∠LBH=∠LBC+∠CBH=∠LBC+∠ABL=∠ABC=90°.∴ LH===BH.∴ AH-CH=AH-AL=LH=BH.
第1题答案
第1题
(3) 将△BEF绕点B旋转一周,H是直线AE与直线CF的交点,连接BH.当∠CFB=45°,AB=3,BE=1时,请直接写出线段CH的长.
解:(3) 当点F在直线BC的右侧时,如图③.∵ BE=BF,∠EBF=90°,∴ ∠FEB=∠EFB=45°.∵ ∠CFB=45°,∴ ∠EFB=∠CFB.
∴ 点E在CF上.∴ 点H与点E重合.过点B作BN⊥CF于点N,则∠BNF=∠BNC=90°.∵ BF=BE=1,∴ EF===. ∴ BN=EN=FN=EF=.∵ BC=AB=3,∴ CN===.∴ CH=CE=CN-EN=.
第1题答案
第1题
当点F在直线BC的左侧时,如图④.设CF与AB交于点P.∵ AB=CB,∠ABE=∠CBF=90°+∠ABF,BE=BF,∴ △ABE≌△CBF.∴ ∠BAE=∠BCF,AE=CF.∵ ∠APF=∠BPC,∴ ∠BAE+∠APF=∠BCF+∠BPC=90°. ∴ ∠AFC=90°.∴ ∠AFC+∠CFB+∠BFE=180°.∴ 点F在AE上.∴ 点H与点F重合.过点B作BQ⊥AE于点Q,则∠BQE=∠BQA=90°.∵ BF=BE=1,∠EBF=90°,∴ EF==.∴ BQ=FQ=EQ=EF=.∵ AB=3,∴ AQ===.∴ CH=CF=AE=AQ+EQ=.综上所述,线段CH的长为或.
第1题答案
第1题
类型2 一线三等角模型
模型1:利用一线三等角构造全等
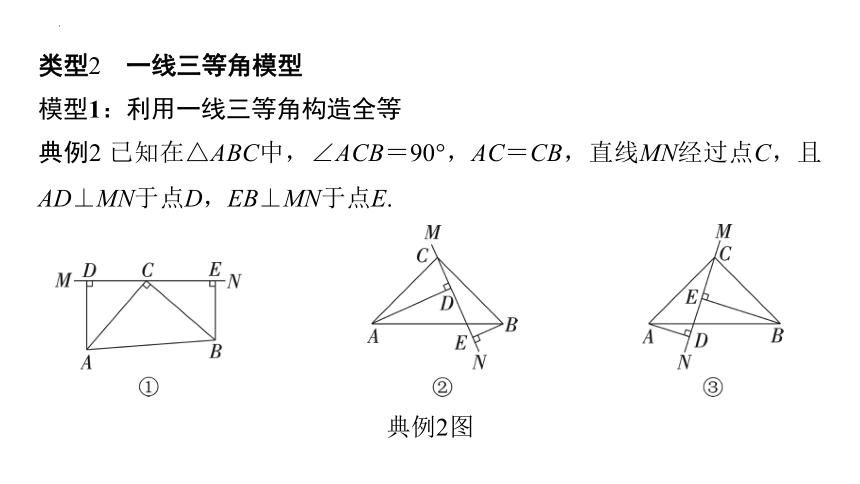
典例2 已知在△ABC中,∠ACB=90°,AC=CB,直线MN经过点C,且AD⊥MN于点D,EB⊥MN于点E.
典例2图
(1) 当直线MN绕点C旋转到如图①所示的位置时,求证:
① △ADC≌△CEB.
② DE=AD+EB.
典例2图
(2) 当直线MN绕点C旋转到如图②所示的位置时,求证:DE=AD-EB.
(3) 当直线MN绕点C旋转到如图③所示的位置时,试问DE,AD,EB具有怎样的等量关系?请写出这个等量关系,并加以证明.
典例2图
[思路点拨] (1) 由∠ACB=90°,得∠ACD+∠BCE=90°;由AD⊥MN,EB⊥MN,得∠ADC=∠CEB=90°,再根据等角的余角相等,得到∠ACD=∠CBE,可得△ADC≌△CEB,得出AD=CE,DC=EB,即可得到DE=CE+DC=AD+EB.(2) 根据等角的余角相等,得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=EB,得出DE=CE-DC=AD-EB.(3) DE,AD,EB具有的等量关系为DE=EB-AD,证明的方法与(2)相同.
解:(1) ① ∵ ∠ACB=90°,∴ ∠ACD+∠BCE=90°.∵ AD⊥MN,EB⊥MN,∴ ∠ADC=∠CEB=90°.∴ ∠BCE+∠CBE=90°.∴ ∠ACD=∠CBE.在△ADC和△CEB中,∵
∴ △ADC≌△CEB.
② ∵ △ADC≌△CEB,∴ AD=CE,DC=EB.∴ DE=CE+DC=AD+EB.
典例2图
(2) ∵ ∠ACB=90°,∴ ∠ACD+∠BCE=90°.∵ AD⊥MN,EB⊥MN,∴ ∠ADC=∠CEB=90°.∴ ∠BCE+∠CBE=90°.∴ ∠ACD=∠CBE.在△ADC和△CEB中,∵
∴ △ADC≌△CEB.∴ AD=CE,DC=EB.∴ DE=CE-DC=AD-EB.
典例2图
(3) DE=EB-AD.∵ 易证△ADC≌△CEB,∴ AD=CE,DC=EB.∴ DE=DC-CE=EB-AD.
典例2图
跟踪训练
2. (2023·芜湖无为一模)数学课上,老师给出了一个模型:如图①,点A在直线DE上,且∠BDA=∠BAC=∠AEC=90°,像这种一条直线上有三个直角顶点的模型,我们把它称为一线三等角模型.
第2题
(1) 如图②,在Rt△ABC中,∠ACB=90°,AC=CB,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.求证:△CDA≌△BEC.
解:(1) ∵ ∠ACB=90°,∴ ∠BCE+∠ACD=90°.∵ AD⊥ED,BE⊥ED,∴ ∠CDA=∠BEC=90°.∴ ∠CBE+∠BCE=90°.∴ ∠ACD=∠CBE.在△CDA和△BEC中,∵
∴ △CDA≌△BEC.
第2题
(2) 如图③,在△ABC中,D是BC上一点,∠CAD=90°,CA=AD,∠DBA=∠DAB,AB=2,求点C到AB的距离.
解:(2) 如图③,过点D作DF⊥AB于点F,过点C作CE⊥AB,交BA的延长线于点E,则∠CEA=∠AFD=90°.∴ ∠DAF+∠ADF=90°.
∵ ∠DBA=∠DAB,∴ BD=AD.∴ AF=BF=AB=.∵ ∠CAD=90°,∴ ∠DAF+∠CAE=90°.∴ ∠CAE=∠ADF.在△CAE和△ADF中,∵ ∴ △CAE≌△ADF.∴ CE=AF=,即点C到AB的距离为.
第2题
模型2:利用一线三等角构造相似
典例3 (2021·安徽)如图①,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,ED∥AB,过点C作CF∥AD,交线段AE于点F,连接BF.
典例3图
(1) 求证:△ABF≌△EAD.
(2) 若AB=9,CD=5,∠ECF=∠AED,求BE的长.
(3) 如图②,若BF的延长线经过AD的中点M,求的值.
典例3图
[思路点拨] (1) 根据题意,得出AB=AE,ED=CD,再证四边形ADCF是平行四边形,得出AF=CD.进而得出AF=ED.由平行线的性质,得∠BAF=∠AED,进而证得结论.(2) 根据△ABF≌△EAD,得出AB=EA=9,AF=ED=5,再得EF=4.根据题意,得到∠EBF=∠EAB,易证△BEF∽△AEB,得到=,进而得到BE的长.(3) 延长BM,ED交于点G.易证△ABE∽△DCE,得出==.设DC=DE=a,CE=b,===x,则AB=AE=ax,AF=DC=a,BE=bx.可得EF=AE-AF=ax-a=a(x-1).再利用△ABF∽△EGF,列方程求解即可.
解:(1) ∵ AE∥CD,∴ ∠AEB=∠BCD.∵ ∠ABC=∠BCD,
∴ ∠ABC=∠AEB.∴ AB=EA.∵ ED∥AB,∴ ∠DEC=∠ABC,∠BAF=∠AED.∵ ∠ABC=∠BCD,∴ ∠DEC=∠BCD.∴ ED=CD.
∵ CF∥AD,AE∥CD,∴ 四边形ADCF是平行四边形.∴ AF=CD.∴ AF=ED.在△ABF和△EAD中,∵ ∴ △ABF≌△EAD.
典例3图
(2) 由(1),知△ABF≌△EAD,ED=CD,AB=EA=9.∴ AF=ED=5,∠ABF=∠EAD.∴ EF=EA-AF=4.∵ CF∥AD,∴ ∠EAD=∠CFE.∴ ∠ABF=∠CFE.∵ ∠ABC=∠AEB,∠ABC=∠ABF+∠EBF,∠AEB=∠CFE+∠ECF,∴ ∠EBF=∠ECF.∵ ∠EAB=∠AED=∠ECF,∴ ∠EBF=∠EAB.∵ ∠BEF=∠AEB,
∴ △BEF∽△AEB.∴ =,即=.∴ BE=6.
典例3图
(3) 如图②,延长BM,ED交于点G.由(1),知四边形ADCF是平行四边形,△ABE,△DCE均为等腰三角形,且∠ABC=∠DCE,∴ AF=DC,△ABE∽△DCE.∴ ==.设DC=DE=a,CE=b,===x,则AB=AE=ax,AF=DC=a,BE=bx.∴ EF=AE-AF=ax-a=a(x-1).∵ AB∥DG,∴ ∠ABG=∠G.∵ M是AD的中点,∴ AM=DM.∵ ∠AMB=∠DMG,∴ △AMB≌△DMG.∴ AB=DG=ax.∴ EG=DG+DE=ax+a=a(x+1).∵ AB∥EG,
∴ △ABF∽△EGF.∴ =,即=.∴ x2-2x-1=0.解得x=1+或x=1-(不合题意,舍去).∴ =x=1+.
典例3图
跟踪训练
3. 如图,在等边三角形ABC中,边长为6,D是边BC上的动点,∠EDF=60°.
(1) 求证:△BDE∽△CFD.
解:(1) ∵ △ABC为等边三角形,∴ ∠B=∠C=60°.
∵ ∠EDF=60°,∴ ∠BED+∠EDB=∠EDB+∠CDF=120°.∴ ∠BED=∠CDF.∴ △BDE∽△CFD.
第3题
(2) 当BD=1,CF=3时,求BE的长.
解:(2) 由(1),知△BDE∽△CFD.∴ =.∵ BC=6,BD=1,∴ CD=BC-BD=5.∴ =.∴ BE=.
第3题
类型3 模型旋转
模型1:“手拉手”旋转构造全等
典例4 如图①,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
典例4图
(1) 判断线段BD与CE的数量关系并证明.
(2) 延长ED交直线BC于点F.
① 如图②,当点F与点B重合时,线段AE,BE和CE之间的数量关系为 AE=BE-CE .
② 如图③,当F为线段BC的中点,且DE=EC时,猜想∠BAD的度数,并说明理由.
AE=BE-CE
典例4图
[思路点拨] (1) 证明△BAD≌△CAE,可得BD=CE.(2) ① AE=DE=BE-BD=BE-CE.② 连接AF,过点A作AG⊥DE于点G,先证明△ABF∽△ADG,得到=,∠BAF=∠DAG,再得出∠BAD=∠FAG,即可证明△ABD∽△AFG,得到∠ADB=90°,由AD=BD,可得∠BAD的度数.
解:(1) BD=CE.∵ △ABC是等边三角形,∴ ∠BAC=60°,AB=AC.∵ AE是由AD绕点A按逆时针方向旋转60°得到的,∴ ∠DAE=60°,AD=AE.∴ ∠BAC=∠DAE.∴ ∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△BAD和△CAE中,
∵ ∴ △BAD≌△CAE.∴ BD=CE.
典例4图
(2) ② ∠BAD=45°.理由:如图③,连接AF,过点A作AG⊥DE于点G,则∠AGD=90°.∵ F为线段BC的中点,△ABC是等边三角形,△ADE是等边三角形,∴ AD=DE,AF⊥BC,∠ABF=∠ADG=60°.∴ ∠AFB=∠AGD.∴ △ABF∽△ADG.∴ =,∠BAF=∠DAG.∴ =,∠BAF+∠DAF=∠DAG+∠DAF.∴ ∠BAD=∠FAG.∴ △ABD∽△AFG.∴ ∠ADB=∠AGF=90°.由(1),得BD=CE.∵ CE=DE=AD,∴ AD=BD.∴ ∠BAD=45°.
典例4图
跟踪训练
4. (2023·池州模拟)如图①,△ABC和△ADE均为等边三角形,连接BD,CE.
第4题
(1) BD与CE的数量关系为 BD=CE ,直线BD与CE所成的锐角的度数为 60° .
BD=CE
60°
(2) 将△ADE绕点A按逆时针方向旋转至如图②所示的位置,分别取BC,DE的中点M,N,连接MN.的值是否随图形的旋转而变化?若不变化,请求出这个值;若变化,请说明理由.
第4题
解:(2) 不变化.如图②,连接AM,AN.∵ △ABC和△ADE均为等边三角形,M,N分别为BC,DE的中点,∴ AM⊥BC,AN⊥DE,∠ABC=∠ADE=∠BAC=∠DAE=60°.∴ =sin60°,=sin60°,∠MAB=∠MAC=∠DAN=∠EAN=30°.∴ =,∠DAN+∠MAD=∠MAB+∠MAD.∴ ∠MAN=∠BAD.∴ △MAN∽△BAD.∴ ==sin60°=.
第4题
(3) 若AB=14,AD=6,当图形旋转至B,D,E三点在同一条直线上时,请直接写出MN的值为 5或8 .
5或8
模型2:半角模型
典例5 在正方形ABCD中,∠MAN=45°,∠MAN绕点A旋转,它的两边分别交直线CB,DC于点M,N.
典例5图
(1) 当∠MAN绕点A旋转到如图①所示的位置时,求证:BM+DN=MN.
(2) 当∠MAN绕点A旋转到如图②所示的位置时,直接写出线段BM,DN和MN之间的数量关系(不需要证明).
典例5图
[思路点拨] (1) 在MB的延长线上截取BE=DN,连接AE,可证△ABE≌△ADN,得到AE=AN,进一步证明△AEM≌△ANM,可得结论BM+DN=MN.(2) 在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,再进一步证明△MAN≌△FAN,得到MN=FN,从而得到结论.
解:(1) 如图①,在MB的延长线上截取BE=DN,连接AE.∵ 四边形ABCD是正方形,∴ AB=AD,∠ABM=∠D=∠BAD=90°=∠ABE.在△ABE和△ADN中,∵ ∴ △ABE≌△ADN.∴ AE=AN,∠EAB=∠NAD.∵ ∠BAD=90°,∠MAN=45°,∴ ∠BAM+∠NAD=45°.∴ ∠BAM+∠EAB=45°.∴ ∠EAM=45°=∠NAM.在△AEM和△ANM中,∵ ∴ △AEM≌△ANM.∴ ME=MN.又∵ ME=BM+BE=BM+DN,∴ BM+DN=MN.
典例5图
(2) DN-BM=MN.
跟踪训练
5. 如图,△ABC是等边三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交边AB,AC于点M,N,连接MN.
(1) 探究BM,MN和NC之间的数量关系,并说明理由.
解:(1) MN=BM+NC.理由:如图,延长AC至点E,使得CE=BM,连接DE.∵ △ABC是等边三角形,
∴ ∠MBC=∠ACB=60°.∵ BD=CD,且∠BDC=120°,
∴ ∠DBC=∠DCB=30°.∴ ∠MBC+∠DBC=∠ACB+∠DCB=60°+30°=90°.∴ ∠MBD=∠DCN=90°.
第5题答案
∴ ∠MBD=∠ECD=90°.在△MBD与△ECD中,BD=CD,∠MBD=∠ECD,BM=CE,∴ △MBD≌△ECD.∴ MD=ED,∠BDM=∠CDE.∵ ∠BDC=120°,∠MDN=60°,∴ ∠BDM+∠CDN=60°.∴ ∠CDE+∠CDN=∠EDN=60°.∴ ∠MDN=∠EDN.又∵ DN=DN,MD=ED,∴ △DMN≌△DEN.∴ MN=EN.∵ EN=CE+NC=BM+NC,∴ MN=BM+NC.
第5题答案
(2) 若△ABC的边长为2,求△AMN的周长.
解:(2) 利用(1)中的结论,得△AMN的周长=AM+MN+AN=(AM+BM)+(NC+AN)=AB+AC=2+2=4.
强化练习
1. 如图,AC=CE,∠ACE=90°,AB⊥BD于点B,ED⊥BD于点D,BD经过点C,AB=6cm,DE=2cm,则BD的长为( B )
A. 6cm B. 8cm C. 10cm D. 4cm
第1题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=4,CD=7,则AC的长为( B )
A. 3 B. 11 C. 15 D. 9
第2题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D.已知AC=16,BC=9,则BD的长为( B )
A. 6 B. 7 C. 8 D. 9
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,AB=AD.若这个四边形的面积是4,则BC+CD的值等于( B )
A. 2 B. 4 C. 2 D. 4
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD,且BD交AC于点O,在BD上取一点E,连接AE,使得AE=AD,∠EAD=∠BAC.若∠ABC=62°,则∠BDC的度数为( A )
A. 56° B. 60° C. 62° D. 64°
第5题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在Rt△ABC中,AB=AC,D,E为边BC上两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后,得到△AFB,连接EF.有下列结论:① △ADC≌△AFB;② △ABE≌△ACD;③ △AED≌△AEF;④ BE+EF=BC-BF.其中,一定正确的个数是( C )
A. 1 B. 2 C. 3 D. 4
第6题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.若AD=8cm,BE=3cm,则DE= 5 cm.
第7题
5
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,在矩形ABCD中,AB=8,BC=12,点E,F分别在BC,CD上.若BE=2,∠EAF=45°,则DF的长是 7.2 .
第8题
7.2
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(1) ∵ 在△ABC中,AB=BC,∠ABC=60°,
∴ △ABC是等边三角形.∴ AC=AB=BC,∠BAC=∠ABC=∠ACB=60°.∵ 线段AC与AD关于直线AP对称,
∴ ∠CAE=∠DAE=15°,AD=AC.∴ ∠BAD=∠BAC+∠CAE+∠DAE=90°.∵ AB=AC=AD,∴ △ABD是等腰直角三角形
9. 如图,在△ABC中,AB=BC,∠ABC=60°,线段AC与AD关于直线AP对称,E是线段BD与直线AP的交点.
(1) 若∠DAE=15°,求证:△ABD是等腰直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 连接CE,求证:BE=AE+CE.
解:(2) 如图,在BE上取点F,使BF=CE,连接AF.∵ 线段AC与AD关于直线AP对称,∴ ∠ACE=∠ADE,∠CAE=∠DAE,AD=AC.∵ AD=AC=AB,∴ ∠D=∠ABD.∴ ∠ABD=∠ACE.在△ABF和△ACE中,∵ ∴ △ABF≌△ACE.∴ AF=AE.∵ ∠D=∠ABD,∠CAE=∠DAE.∴ ∠AEB=∠D+∠DAE=(∠D+∠ABD+∠DAC)=(180°-∠BAC)=60°.∴ 在△AFE中,AF=AE,∠AEF=60°.∴ △AFE是等边三角形.∴ AF=FE.∴ BE=FE+BF=AE+CE
第9题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,O是直线MN上一点,∠AOB=90°,过点A作AC⊥MN于点C,过点B作BD⊥MN于点D.
(1) 求证:△AOC∽△OBD.
解:(1) ∵ AC⊥MN,BD⊥MN,∴ ∠ACO=∠ODB=90°.又∵ ∠AOB=90°,∴ ∠A+∠AOC=∠BOD+∠AOC=90°.∴ ∠A=∠BOD.
∴ △AOC∽△OBD
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 若OA=5,OC=OD=3,求BD的长.
解:(2) 在Rt△ACO中,AC===4.∵ △AOC∽△OBD,∴ =.∴ =.∴ BD=
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 旋转变换是解决数学问题的一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.如图,在△ABC中,AB=AC,∠BAC=α,点D,E在边BC上,且∠DAE=α.
第11题
1
2
3
4
5
6
7
8
9
10
11
12
13
① ∠DAF= 30° .
② 求证:DF=DE.
解:(1) ② 由①,知AF=AE,∠DAF=∠DAE=30°.又∵ AD=AD,∴ △DAF≌△DAE.∴ DF=DE
30°
(1) 如图①,当α=60°时,将△AEC绕点A按顺时针方向旋转60°到△AFB的位置,连接DF.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 如图②,当α=90°时,猜想BD,DE,CE之间的数量关系,并说明理由.
解:(2) DE2=BD2+CE2 理由:如图②,将△AEC绕点A按顺时针方向旋转90°到△AFB的位置,连接DF,则△BAF≌△CAE,∠EAF=90°.∴ AF=AE,∠BAF=∠CAE,BF=CE,∠ABF=∠C.在Rt△ABC中,∠C=∠ABC=45°.∴ ∠ABF=45°.∴ ∠DBF=90°.根据勾股定理,得DF2=BD2+BF2.∴ DF2=BD2+CE2.同(1)②的方法,可得DF=DE.∴ DE2=BD2+CE2.
第11题
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并把它们的底角顶点连接起来,那么会形成一组全等的三角形.小明把具有这个规律的图形称为“手拉手”图形.
(1) 问题发现:如图①,若△ABC和△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
第12题
解:(1) ∵ △ABC和△ADE均是顶角为40°的等腰三角形,∴ AB=AC,AD=AE,∠BAC=∠DAE.∴ ∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE.∴ △BAD≌△CAE.∴ BD=CE
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 拓展探究:如图②,若△ACB和△DCE均为等边三角形,点A,D,E在同一条直线上,连接BE,则∠AEB的度数为 60° ,线段BE与AD之间的数量关系是 AD=BE .
60°
AD=BE
1
2
3
4
5
6
7
8
9
10
11
12
13
(3) 解决问题:如图③,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE的边DE上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
解:(3) ∠AEB=90°,AE=BE+2CM 理由:同(1)(2)的方法,可得△ACD≌△BCE.∴ AD=BE,∠ADC=∠BEC.∵ △CDE是等腰直角三角形,∴ ∠CDE=∠CED=45°.∴ ∠ADC=180°-∠CDE=135°.∴ ∠BEC=∠ADC=135°.∴ ∠AEB=∠BEC-∠CED=135°-45°=90°.∵ CD=CE,CM⊥DE,∴ DM=ME.∵ ∠DCE=90°,
∴ DM=ME=CM.∴ AE=AD+DE=BE+2CM.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,AB=AC,D,A,E三点都在直线m上,∠BDA=∠AEC=∠BAC.
(1) 如图①,若AB⊥AC,则BD与AE之间的数量关系为 BD=AE ,BD,CE,DE之间的数量关系为 BD+CE=DE .
第13题
BD=
AE
BD+CE=DE
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 如图②,当AB不垂直于AC时,(1)中的结论是否成立?请说明理由.
解:(2) 成立 理由:∵ ∠BDA=∠AEC=∠BAC,∠BAD+∠CAE+∠BAC=∠BAD+∠ABD+∠BDA=180°,∴ ∠CAE=∠ABD.
又∵ AB=CA,∴ △ABD≌△CAE.∴ BD=AE,AD=CE.∵ AE+AD=DE,∴ BD+CE=DE.
1
2
3
4
5
6
7
8
9
10
11
12
13
(3) 如图③,若只保持∠BDA=∠AEC,且BD=EF=7cm,DE=10cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时点C在线段EF上以xcm/s的速度由点E向点F运动,设点A,C的运动时间为ts.是否存在t,x,使得△ABD与△EAC全等?若存在,求出相应的t与x的值;若不存在,请说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(3) 存在 当△DAB≌△ECA时,AD=CE,BD=AE=7cm.
∵ AD+AE=DE=10cm,∴ CE=AD=DE-AE=3cm.∴ t==.∴ x=3÷=2.当△DAB≌△EAC时,AD=AE=DE=5cm,DB=EC=7cm.∴ t==.∴ x=7÷=.综上所述,存在t,x,使得△ABD与△EAC全等,t=,x=2或t=,x=
1
2
3
4
5
6
7
8
9
10
11
12
13
专题五 几何探究题
类型1 利用截长补短法构造线段的和与差
典例1 如图,四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.
(1) 求证:BD⊥EC.
(2) 若AB=1,求AE的长.
(3) 连接AG.求证:EG-DG=AG.
[思路点拨] (1) 证明△AEF≌△ADB,得出∠AEF=∠ADB,证得∠EGB=90°,可得出结论.(2) 证明△AEF∽△DCF,得出=,即AE·DF=AF·DC.设AE=AD=a(a>0),则有a(a-1)=1,解方程即可得出答案.(3) 在线段EG上取点P,使得EP=DG,连接AP,证明△AEP≌△ADG,得出AP=AG,∠EAP=∠DAG,证得△PAG为等腰直角三角形,即可得出结论.
解:(1) ∵ 四边形ABCD是矩形,点E在BA的延长线上,∴ ∠EAF=∠DAB=90°.又∵ AE=AD,AF=AB,∴ △AEF≌△ADB.∴ ∠AEF=∠ADB.∴ ∠GEB+∠GBE=∠ADB+∠ABD=90°.∴ ∠EGB=90°.
∴ BD⊥EC.
(2) ∵ 四边形ABCD是矩形,∴ AE∥CD,CD=AB=1.∴ ∠AEF=∠DCF,∠EAF=∠CDF.∴ △AEF∽△DCF.∴ =,即AE·DF=AF·DC.设AE=AD=a(a>0),则a(a-1)=1.化简,得a2-a-1=0,解得a=或a=(不合题意,舍去).∴ AE=.
(3) 如图,在线段EG上取点P,使得EP=DG,连接AP.在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴ △AEP≌△ADG.∴ AP=AG,∠EAP=∠DAG.∴ ∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°.∴ △PAG为等腰直角三角形.
∴ PG=AG.∴ EG-DG=EG-EP=PG=AG.
典例1图答案
跟踪训练
1. (2023·亳州蒙城二模)已知四边形ABCD是正方形,以B为顶点作等腰直角三角形BEF,BE=BF,连接AE,CF.
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(1) 如图①,当点E在BC上时,请判断AE和CF之间的数量及位置关系,并说明理由.
解:(1) AE=CF,AE⊥CF 理由:如图①,延长AE交CF于点G.
∵ 四边形ABCD是正方形,点E在BC上,∴ AB=CB,∠ABE=90°.∵ BE=BF,∠EBF=90°,∴ ∠ABE=∠CBF=90°.∴ △ABE≌△CBF.
∴ AE=CF,∠BAE=∠BCF.∵ ∠CEG=∠AEB,∴ ∠BCF+∠CEG=∠BAE+∠AEB=90°.∴ ∠CGE=90°.∴ AE⊥CF.
第1题答案
第1题
(2) 如图②,H是AE的延长线与直线CF的交点,连接BH,将△BEF绕点B旋转.当点F在直线BC的右侧时,求证:AH-CH=BH.
解:(2) 如图②,在AH上取点L,使得AL=CH,连接BL.∵ AB=CB,∠ABE=∠CBF=90°-∠CBE,BE=BF,∴ △ABE≌△CBF.
∴ ∠BAE=∠BCF,即∠BAL=∠BCH.又∵ AB=CB,AL=CH,
∴ △BAL≌△BCH.∴ BL=BH,∠ABL=∠CBH.∴ ∠LBH=∠LBC+∠CBH=∠LBC+∠ABL=∠ABC=90°.∴ LH===BH.∴ AH-CH=AH-AL=LH=BH.
第1题答案
第1题
(3) 将△BEF绕点B旋转一周,H是直线AE与直线CF的交点,连接BH.当∠CFB=45°,AB=3,BE=1时,请直接写出线段CH的长.
解:(3) 当点F在直线BC的右侧时,如图③.∵ BE=BF,∠EBF=90°,∴ ∠FEB=∠EFB=45°.∵ ∠CFB=45°,∴ ∠EFB=∠CFB.
∴ 点E在CF上.∴ 点H与点E重合.过点B作BN⊥CF于点N,则∠BNF=∠BNC=90°.∵ BF=BE=1,∴ EF===. ∴ BN=EN=FN=EF=.∵ BC=AB=3,∴ CN===.∴ CH=CE=CN-EN=.
第1题答案
第1题
当点F在直线BC的左侧时,如图④.设CF与AB交于点P.∵ AB=CB,∠ABE=∠CBF=90°+∠ABF,BE=BF,∴ △ABE≌△CBF.∴ ∠BAE=∠BCF,AE=CF.∵ ∠APF=∠BPC,∴ ∠BAE+∠APF=∠BCF+∠BPC=90°. ∴ ∠AFC=90°.∴ ∠AFC+∠CFB+∠BFE=180°.∴ 点F在AE上.∴ 点H与点F重合.过点B作BQ⊥AE于点Q,则∠BQE=∠BQA=90°.∵ BF=BE=1,∠EBF=90°,∴ EF==.∴ BQ=FQ=EQ=EF=.∵ AB=3,∴ AQ===.∴ CH=CF=AE=AQ+EQ=.综上所述,线段CH的长为或.
第1题答案
第1题
类型2 一线三等角模型
模型1:利用一线三等角构造全等
典例2 已知在△ABC中,∠ACB=90°,AC=CB,直线MN经过点C,且AD⊥MN于点D,EB⊥MN于点E.
典例2图
(1) 当直线MN绕点C旋转到如图①所示的位置时,求证:
① △ADC≌△CEB.
② DE=AD+EB.
典例2图
(2) 当直线MN绕点C旋转到如图②所示的位置时,求证:DE=AD-EB.
(3) 当直线MN绕点C旋转到如图③所示的位置时,试问DE,AD,EB具有怎样的等量关系?请写出这个等量关系,并加以证明.
典例2图
[思路点拨] (1) 由∠ACB=90°,得∠ACD+∠BCE=90°;由AD⊥MN,EB⊥MN,得∠ADC=∠CEB=90°,再根据等角的余角相等,得到∠ACD=∠CBE,可得△ADC≌△CEB,得出AD=CE,DC=EB,即可得到DE=CE+DC=AD+EB.(2) 根据等角的余角相等,得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=EB,得出DE=CE-DC=AD-EB.(3) DE,AD,EB具有的等量关系为DE=EB-AD,证明的方法与(2)相同.
解:(1) ① ∵ ∠ACB=90°,∴ ∠ACD+∠BCE=90°.∵ AD⊥MN,EB⊥MN,∴ ∠ADC=∠CEB=90°.∴ ∠BCE+∠CBE=90°.∴ ∠ACD=∠CBE.在△ADC和△CEB中,∵
∴ △ADC≌△CEB.
② ∵ △ADC≌△CEB,∴ AD=CE,DC=EB.∴ DE=CE+DC=AD+EB.
典例2图
(2) ∵ ∠ACB=90°,∴ ∠ACD+∠BCE=90°.∵ AD⊥MN,EB⊥MN,∴ ∠ADC=∠CEB=90°.∴ ∠BCE+∠CBE=90°.∴ ∠ACD=∠CBE.在△ADC和△CEB中,∵
∴ △ADC≌△CEB.∴ AD=CE,DC=EB.∴ DE=CE-DC=AD-EB.
典例2图
(3) DE=EB-AD.∵ 易证△ADC≌△CEB,∴ AD=CE,DC=EB.∴ DE=DC-CE=EB-AD.
典例2图
跟踪训练
2. (2023·芜湖无为一模)数学课上,老师给出了一个模型:如图①,点A在直线DE上,且∠BDA=∠BAC=∠AEC=90°,像这种一条直线上有三个直角顶点的模型,我们把它称为一线三等角模型.
第2题
(1) 如图②,在Rt△ABC中,∠ACB=90°,AC=CB,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.求证:△CDA≌△BEC.
解:(1) ∵ ∠ACB=90°,∴ ∠BCE+∠ACD=90°.∵ AD⊥ED,BE⊥ED,∴ ∠CDA=∠BEC=90°.∴ ∠CBE+∠BCE=90°.∴ ∠ACD=∠CBE.在△CDA和△BEC中,∵
∴ △CDA≌△BEC.
第2题
(2) 如图③,在△ABC中,D是BC上一点,∠CAD=90°,CA=AD,∠DBA=∠DAB,AB=2,求点C到AB的距离.
解:(2) 如图③,过点D作DF⊥AB于点F,过点C作CE⊥AB,交BA的延长线于点E,则∠CEA=∠AFD=90°.∴ ∠DAF+∠ADF=90°.
∵ ∠DBA=∠DAB,∴ BD=AD.∴ AF=BF=AB=.∵ ∠CAD=90°,∴ ∠DAF+∠CAE=90°.∴ ∠CAE=∠ADF.在△CAE和△ADF中,∵ ∴ △CAE≌△ADF.∴ CE=AF=,即点C到AB的距离为.
第2题
模型2:利用一线三等角构造相似
典例3 (2021·安徽)如图①,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,ED∥AB,过点C作CF∥AD,交线段AE于点F,连接BF.
典例3图
(1) 求证:△ABF≌△EAD.
(2) 若AB=9,CD=5,∠ECF=∠AED,求BE的长.
(3) 如图②,若BF的延长线经过AD的中点M,求的值.
典例3图
[思路点拨] (1) 根据题意,得出AB=AE,ED=CD,再证四边形ADCF是平行四边形,得出AF=CD.进而得出AF=ED.由平行线的性质,得∠BAF=∠AED,进而证得结论.(2) 根据△ABF≌△EAD,得出AB=EA=9,AF=ED=5,再得EF=4.根据题意,得到∠EBF=∠EAB,易证△BEF∽△AEB,得到=,进而得到BE的长.(3) 延长BM,ED交于点G.易证△ABE∽△DCE,得出==.设DC=DE=a,CE=b,===x,则AB=AE=ax,AF=DC=a,BE=bx.可得EF=AE-AF=ax-a=a(x-1).再利用△ABF∽△EGF,列方程求解即可.
解:(1) ∵ AE∥CD,∴ ∠AEB=∠BCD.∵ ∠ABC=∠BCD,
∴ ∠ABC=∠AEB.∴ AB=EA.∵ ED∥AB,∴ ∠DEC=∠ABC,∠BAF=∠AED.∵ ∠ABC=∠BCD,∴ ∠DEC=∠BCD.∴ ED=CD.
∵ CF∥AD,AE∥CD,∴ 四边形ADCF是平行四边形.∴ AF=CD.∴ AF=ED.在△ABF和△EAD中,∵ ∴ △ABF≌△EAD.
典例3图
(2) 由(1),知△ABF≌△EAD,ED=CD,AB=EA=9.∴ AF=ED=5,∠ABF=∠EAD.∴ EF=EA-AF=4.∵ CF∥AD,∴ ∠EAD=∠CFE.∴ ∠ABF=∠CFE.∵ ∠ABC=∠AEB,∠ABC=∠ABF+∠EBF,∠AEB=∠CFE+∠ECF,∴ ∠EBF=∠ECF.∵ ∠EAB=∠AED=∠ECF,∴ ∠EBF=∠EAB.∵ ∠BEF=∠AEB,
∴ △BEF∽△AEB.∴ =,即=.∴ BE=6.
典例3图
(3) 如图②,延长BM,ED交于点G.由(1),知四边形ADCF是平行四边形,△ABE,△DCE均为等腰三角形,且∠ABC=∠DCE,∴ AF=DC,△ABE∽△DCE.∴ ==.设DC=DE=a,CE=b,===x,则AB=AE=ax,AF=DC=a,BE=bx.∴ EF=AE-AF=ax-a=a(x-1).∵ AB∥DG,∴ ∠ABG=∠G.∵ M是AD的中点,∴ AM=DM.∵ ∠AMB=∠DMG,∴ △AMB≌△DMG.∴ AB=DG=ax.∴ EG=DG+DE=ax+a=a(x+1).∵ AB∥EG,
∴ △ABF∽△EGF.∴ =,即=.∴ x2-2x-1=0.解得x=1+或x=1-(不合题意,舍去).∴ =x=1+.
典例3图
跟踪训练
3. 如图,在等边三角形ABC中,边长为6,D是边BC上的动点,∠EDF=60°.
(1) 求证:△BDE∽△CFD.
解:(1) ∵ △ABC为等边三角形,∴ ∠B=∠C=60°.
∵ ∠EDF=60°,∴ ∠BED+∠EDB=∠EDB+∠CDF=120°.∴ ∠BED=∠CDF.∴ △BDE∽△CFD.
第3题
(2) 当BD=1,CF=3时,求BE的长.
解:(2) 由(1),知△BDE∽△CFD.∴ =.∵ BC=6,BD=1,∴ CD=BC-BD=5.∴ =.∴ BE=.
第3题
类型3 模型旋转
模型1:“手拉手”旋转构造全等
典例4 如图①,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
典例4图
(1) 判断线段BD与CE的数量关系并证明.
(2) 延长ED交直线BC于点F.
① 如图②,当点F与点B重合时,线段AE,BE和CE之间的数量关系为 AE=BE-CE .
② 如图③,当F为线段BC的中点,且DE=EC时,猜想∠BAD的度数,并说明理由.
AE=BE-CE
典例4图
[思路点拨] (1) 证明△BAD≌△CAE,可得BD=CE.(2) ① AE=DE=BE-BD=BE-CE.② 连接AF,过点A作AG⊥DE于点G,先证明△ABF∽△ADG,得到=,∠BAF=∠DAG,再得出∠BAD=∠FAG,即可证明△ABD∽△AFG,得到∠ADB=90°,由AD=BD,可得∠BAD的度数.
解:(1) BD=CE.∵ △ABC是等边三角形,∴ ∠BAC=60°,AB=AC.∵ AE是由AD绕点A按逆时针方向旋转60°得到的,∴ ∠DAE=60°,AD=AE.∴ ∠BAC=∠DAE.∴ ∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△BAD和△CAE中,
∵ ∴ △BAD≌△CAE.∴ BD=CE.
典例4图
(2) ② ∠BAD=45°.理由:如图③,连接AF,过点A作AG⊥DE于点G,则∠AGD=90°.∵ F为线段BC的中点,△ABC是等边三角形,△ADE是等边三角形,∴ AD=DE,AF⊥BC,∠ABF=∠ADG=60°.∴ ∠AFB=∠AGD.∴ △ABF∽△ADG.∴ =,∠BAF=∠DAG.∴ =,∠BAF+∠DAF=∠DAG+∠DAF.∴ ∠BAD=∠FAG.∴ △ABD∽△AFG.∴ ∠ADB=∠AGF=90°.由(1),得BD=CE.∵ CE=DE=AD,∴ AD=BD.∴ ∠BAD=45°.
典例4图
跟踪训练
4. (2023·池州模拟)如图①,△ABC和△ADE均为等边三角形,连接BD,CE.
第4题
(1) BD与CE的数量关系为 BD=CE ,直线BD与CE所成的锐角的度数为 60° .
BD=CE
60°
(2) 将△ADE绕点A按逆时针方向旋转至如图②所示的位置,分别取BC,DE的中点M,N,连接MN.的值是否随图形的旋转而变化?若不变化,请求出这个值;若变化,请说明理由.
第4题
解:(2) 不变化.如图②,连接AM,AN.∵ △ABC和△ADE均为等边三角形,M,N分别为BC,DE的中点,∴ AM⊥BC,AN⊥DE,∠ABC=∠ADE=∠BAC=∠DAE=60°.∴ =sin60°,=sin60°,∠MAB=∠MAC=∠DAN=∠EAN=30°.∴ =,∠DAN+∠MAD=∠MAB+∠MAD.∴ ∠MAN=∠BAD.∴ △MAN∽△BAD.∴ ==sin60°=.
第4题
(3) 若AB=14,AD=6,当图形旋转至B,D,E三点在同一条直线上时,请直接写出MN的值为 5或8 .
5或8
模型2:半角模型
典例5 在正方形ABCD中,∠MAN=45°,∠MAN绕点A旋转,它的两边分别交直线CB,DC于点M,N.
典例5图
(1) 当∠MAN绕点A旋转到如图①所示的位置时,求证:BM+DN=MN.
(2) 当∠MAN绕点A旋转到如图②所示的位置时,直接写出线段BM,DN和MN之间的数量关系(不需要证明).
典例5图
[思路点拨] (1) 在MB的延长线上截取BE=DN,连接AE,可证△ABE≌△ADN,得到AE=AN,进一步证明△AEM≌△ANM,可得结论BM+DN=MN.(2) 在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,再进一步证明△MAN≌△FAN,得到MN=FN,从而得到结论.
解:(1) 如图①,在MB的延长线上截取BE=DN,连接AE.∵ 四边形ABCD是正方形,∴ AB=AD,∠ABM=∠D=∠BAD=90°=∠ABE.在△ABE和△ADN中,∵ ∴ △ABE≌△ADN.∴ AE=AN,∠EAB=∠NAD.∵ ∠BAD=90°,∠MAN=45°,∴ ∠BAM+∠NAD=45°.∴ ∠BAM+∠EAB=45°.∴ ∠EAM=45°=∠NAM.在△AEM和△ANM中,∵ ∴ △AEM≌△ANM.∴ ME=MN.又∵ ME=BM+BE=BM+DN,∴ BM+DN=MN.
典例5图
(2) DN-BM=MN.
跟踪训练
5. 如图,△ABC是等边三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交边AB,AC于点M,N,连接MN.
(1) 探究BM,MN和NC之间的数量关系,并说明理由.
解:(1) MN=BM+NC.理由:如图,延长AC至点E,使得CE=BM,连接DE.∵ △ABC是等边三角形,
∴ ∠MBC=∠ACB=60°.∵ BD=CD,且∠BDC=120°,
∴ ∠DBC=∠DCB=30°.∴ ∠MBC+∠DBC=∠ACB+∠DCB=60°+30°=90°.∴ ∠MBD=∠DCN=90°.
第5题答案
∴ ∠MBD=∠ECD=90°.在△MBD与△ECD中,BD=CD,∠MBD=∠ECD,BM=CE,∴ △MBD≌△ECD.∴ MD=ED,∠BDM=∠CDE.∵ ∠BDC=120°,∠MDN=60°,∴ ∠BDM+∠CDN=60°.∴ ∠CDE+∠CDN=∠EDN=60°.∴ ∠MDN=∠EDN.又∵ DN=DN,MD=ED,∴ △DMN≌△DEN.∴ MN=EN.∵ EN=CE+NC=BM+NC,∴ MN=BM+NC.
第5题答案
(2) 若△ABC的边长为2,求△AMN的周长.
解:(2) 利用(1)中的结论,得△AMN的周长=AM+MN+AN=(AM+BM)+(NC+AN)=AB+AC=2+2=4.
强化练习
1. 如图,AC=CE,∠ACE=90°,AB⊥BD于点B,ED⊥BD于点D,BD经过点C,AB=6cm,DE=2cm,则BD的长为( B )
A. 6cm B. 8cm C. 10cm D. 4cm
第1题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,在△ABC中,AD平分∠BAC,∠B=2∠ADB,AB=4,CD=7,则AC的长为( B )
A. 3 B. 11 C. 15 D. 9
第2题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D.已知AC=16,BC=9,则BD的长为( B )
A. 6 B. 7 C. 8 D. 9
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,AB=AD.若这个四边形的面积是4,则BC+CD的值等于( B )
A. 2 B. 4 C. 2 D. 4
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,在△ABC中,AB=AC,D是△ABC外一点,连接AD,BD,CD,且BD交AC于点O,在BD上取一点E,连接AE,使得AE=AD,∠EAD=∠BAC.若∠ABC=62°,则∠BDC的度数为( A )
A. 56° B. 60° C. 62° D. 64°
第5题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在Rt△ABC中,AB=AC,D,E为边BC上两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后,得到△AFB,连接EF.有下列结论:① △ADC≌△AFB;② △ABE≌△ACD;③ △AED≌△AEF;④ BE+EF=BC-BF.其中,一定正确的个数是( C )
A. 1 B. 2 C. 3 D. 4
第6题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.若AD=8cm,BE=3cm,则DE= 5 cm.
第7题
5
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,在矩形ABCD中,AB=8,BC=12,点E,F分别在BC,CD上.若BE=2,∠EAF=45°,则DF的长是 7.2 .
第8题
7.2
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(1) ∵ 在△ABC中,AB=BC,∠ABC=60°,
∴ △ABC是等边三角形.∴ AC=AB=BC,∠BAC=∠ABC=∠ACB=60°.∵ 线段AC与AD关于直线AP对称,
∴ ∠CAE=∠DAE=15°,AD=AC.∴ ∠BAD=∠BAC+∠CAE+∠DAE=90°.∵ AB=AC=AD,∴ △ABD是等腰直角三角形
9. 如图,在△ABC中,AB=BC,∠ABC=60°,线段AC与AD关于直线AP对称,E是线段BD与直线AP的交点.
(1) 若∠DAE=15°,求证:△ABD是等腰直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 连接CE,求证:BE=AE+CE.
解:(2) 如图,在BE上取点F,使BF=CE,连接AF.∵ 线段AC与AD关于直线AP对称,∴ ∠ACE=∠ADE,∠CAE=∠DAE,AD=AC.∵ AD=AC=AB,∴ ∠D=∠ABD.∴ ∠ABD=∠ACE.在△ABF和△ACE中,∵ ∴ △ABF≌△ACE.∴ AF=AE.∵ ∠D=∠ABD,∠CAE=∠DAE.∴ ∠AEB=∠D+∠DAE=(∠D+∠ABD+∠DAC)=(180°-∠BAC)=60°.∴ 在△AFE中,AF=AE,∠AEF=60°.∴ △AFE是等边三角形.∴ AF=FE.∴ BE=FE+BF=AE+CE
第9题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,O是直线MN上一点,∠AOB=90°,过点A作AC⊥MN于点C,过点B作BD⊥MN于点D.
(1) 求证:△AOC∽△OBD.
解:(1) ∵ AC⊥MN,BD⊥MN,∴ ∠ACO=∠ODB=90°.又∵ ∠AOB=90°,∴ ∠A+∠AOC=∠BOD+∠AOC=90°.∴ ∠A=∠BOD.
∴ △AOC∽△OBD
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 若OA=5,OC=OD=3,求BD的长.
解:(2) 在Rt△ACO中,AC===4.∵ △AOC∽△OBD,∴ =.∴ =.∴ BD=
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 旋转变换是解决数学问题的一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.如图,在△ABC中,AB=AC,∠BAC=α,点D,E在边BC上,且∠DAE=α.
第11题
1
2
3
4
5
6
7
8
9
10
11
12
13
① ∠DAF= 30° .
② 求证:DF=DE.
解:(1) ② 由①,知AF=AE,∠DAF=∠DAE=30°.又∵ AD=AD,∴ △DAF≌△DAE.∴ DF=DE
30°
(1) 如图①,当α=60°时,将△AEC绕点A按顺时针方向旋转60°到△AFB的位置,连接DF.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 如图②,当α=90°时,猜想BD,DE,CE之间的数量关系,并说明理由.
解:(2) DE2=BD2+CE2 理由:如图②,将△AEC绕点A按顺时针方向旋转90°到△AFB的位置,连接DF,则△BAF≌△CAE,∠EAF=90°.∴ AF=AE,∠BAF=∠CAE,BF=CE,∠ABF=∠C.在Rt△ABC中,∠C=∠ABC=45°.∴ ∠ABF=45°.∴ ∠DBF=90°.根据勾股定理,得DF2=BD2+BF2.∴ DF2=BD2+CE2.同(1)②的方法,可得DF=DE.∴ DE2=BD2+CE2.
第11题
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并把它们的底角顶点连接起来,那么会形成一组全等的三角形.小明把具有这个规律的图形称为“手拉手”图形.
(1) 问题发现:如图①,若△ABC和△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
第12题
解:(1) ∵ △ABC和△ADE均是顶角为40°的等腰三角形,∴ AB=AC,AD=AE,∠BAC=∠DAE.∴ ∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE.∴ △BAD≌△CAE.∴ BD=CE
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 拓展探究:如图②,若△ACB和△DCE均为等边三角形,点A,D,E在同一条直线上,连接BE,则∠AEB的度数为 60° ,线段BE与AD之间的数量关系是 AD=BE .
60°
AD=BE
1
2
3
4
5
6
7
8
9
10
11
12
13
(3) 解决问题:如图③,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE的边DE上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
解:(3) ∠AEB=90°,AE=BE+2CM 理由:同(1)(2)的方法,可得△ACD≌△BCE.∴ AD=BE,∠ADC=∠BEC.∵ △CDE是等腰直角三角形,∴ ∠CDE=∠CED=45°.∴ ∠ADC=180°-∠CDE=135°.∴ ∠BEC=∠ADC=135°.∴ ∠AEB=∠BEC-∠CED=135°-45°=90°.∵ CD=CE,CM⊥DE,∴ DM=ME.∵ ∠DCE=90°,
∴ DM=ME=CM.∴ AE=AD+DE=BE+2CM.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,AB=AC,D,A,E三点都在直线m上,∠BDA=∠AEC=∠BAC.
(1) 如图①,若AB⊥AC,则BD与AE之间的数量关系为 BD=AE ,BD,CE,DE之间的数量关系为 BD+CE=DE .
第13题
BD=
AE
BD+CE=DE
1
2
3
4
5
6
7
8
9
10
11
12
13
(2) 如图②,当AB不垂直于AC时,(1)中的结论是否成立?请说明理由.
解:(2) 成立 理由:∵ ∠BDA=∠AEC=∠BAC,∠BAD+∠CAE+∠BAC=∠BAD+∠ABD+∠BDA=180°,∴ ∠CAE=∠ABD.
又∵ AB=CA,∴ △ABD≌△CAE.∴ BD=AE,AD=CE.∵ AE+AD=DE,∴ BD+CE=DE.
1
2
3
4
5
6
7
8
9
10
11
12
13
(3) 如图③,若只保持∠BDA=∠AEC,且BD=EF=7cm,DE=10cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时点C在线段EF上以xcm/s的速度由点E向点F运动,设点A,C的运动时间为ts.是否存在t,x,使得△ABD与△EAC全等?若存在,求出相应的t与x的值;若不存在,请说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
解:(3) 存在 当△DAB≌△ECA时,AD=CE,BD=AE=7cm.
∵ AD+AE=DE=10cm,∴ CE=AD=DE-AE=3cm.∴ t==.∴ x=3÷=2.当△DAB≌△EAC时,AD=AE=DE=5cm,DB=EC=7cm.∴ t==.∴ x=7÷=.综上所述,存在t,x,使得△ABD与△EAC全等,t=,x=2或t=,x=
1
2
3
4
5
6
7
8
9
10
11
12
13
同课章节目录
