2024年中考数学二轮复习题型突破课件:与中点有关的辅助线问题(共22张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:与中点有关的辅助线问题(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 915.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:42:22 | ||
图片预览





文档简介
(共22张PPT)
与中点有关的辅助线问题
类型1 构造中线
方法指导:(1) 当题目中已知直角三角形与斜边的中点时,可尝试连接直角顶点与斜边的中点,利用“直角三角形斜边上的中线等于斜边的一半”解题;(2) 当题目中已知等腰三角形与底边的中点时,可连接等腰三角形的顶角顶点与底边的中点,利用“三线合一”解题.
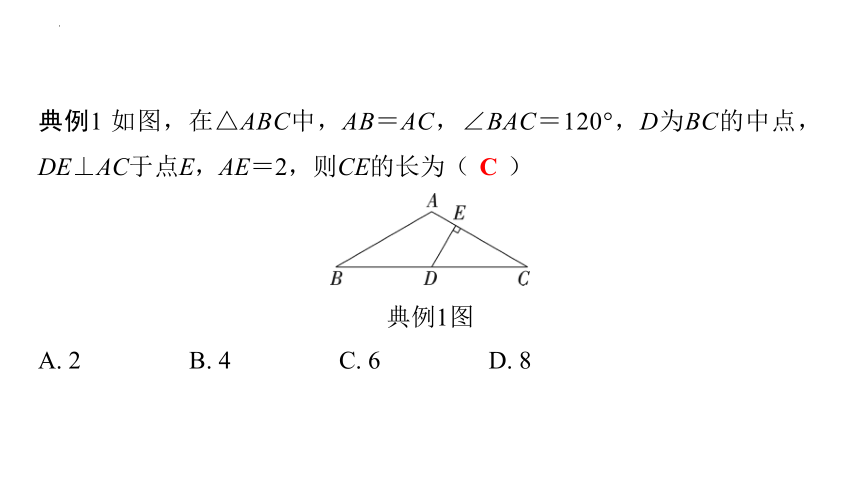
典例1 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,则CE的长为( C )
典例1图
A. 2 B. 4 C. 6 D. 8
C
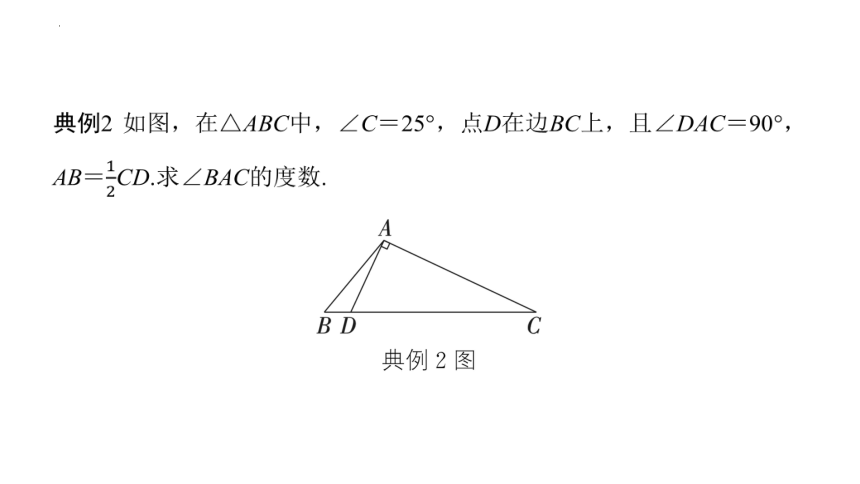
典例2 如图,在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=CD.求∠BAC的度数.
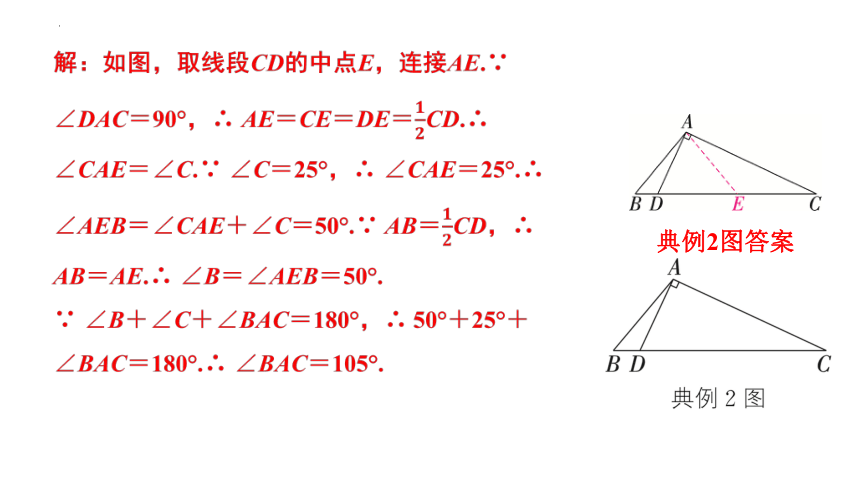
解:如图,取线段CD的中点E,连接AE.∵ ∠DAC=90°,∴ AE=CE=DE=CD.∴ ∠CAE=∠C.∵ ∠C=25°,∴ ∠CAE=25°.∴ ∠AEB=∠CAE+∠C=50°.∵ AB=CD,∴ AB=AE.∴ ∠B=∠AEB=50°.
∵ ∠B+∠C+∠BAC=180°,∴ 50°+25°+∠BAC=180°.∴ ∠BAC=105°.
典例2图答案
类型2倍长中线
方法指导:当题目中已知三角形一边上的中线时,可尝试将此中线延长至它的一倍,构造全等三角形,利用全等三角形的性质解题.
典例3 如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长,交AC于点E.若AE=EF,求证:AC=BF.
典例3图答案
解:如图,延长AD至点H,使DH=AD,连接BH.∵ AD是△ABC的中线,∴ CD=BD.又∵ ∠ADC=∠HDB,AD=HD,
∴ △ADC≌△HDB.∴ AC=HB,∠CAD=∠H.∵ AE=EF,∴ ∠EAF=∠AFE.∴ ∠H=∠AFE.又∵ ∠AFE=∠BFH,∴ ∠H=∠BFH.∴ BF=BH.∴ AC=BF.
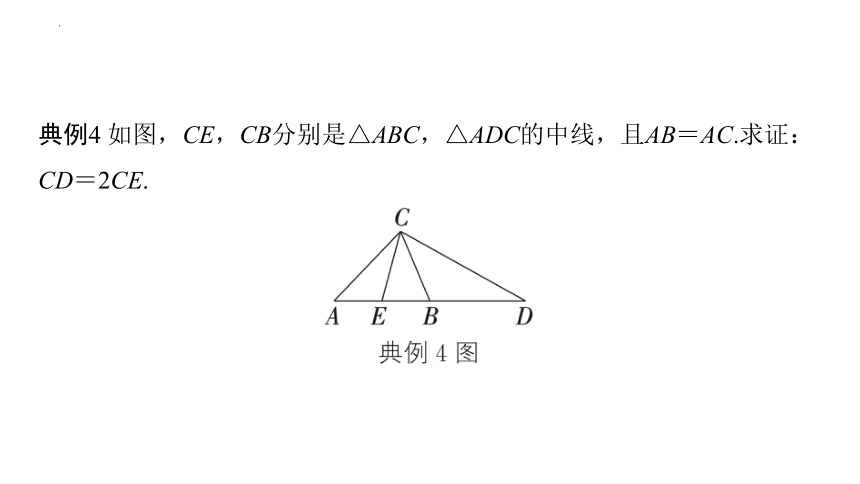
典例4 如图,CE,CB分别是△ABC,△ADC的中线,且AB=AC.求证:CD=2CE.
解:如图,延长CE到点F,使EF=CE,连接BF,则CF=2CE.∵ CE是△ABC的中线,∴ BE=AE.在△BEF和△AEC中,
∵ ∴ △BEF≌△AEC.∴ ∠EBF=∠A,BF=AC.∵ AB=AC,∴ ∠ABC=∠ACB.∴ ∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.∵ CB是△ADC的中线,∴ AB=BD.又∵ AB=AC,AC=BF,∴ AB=BF.∴ BF=BD.在△CBF和△CBD中,
∵ ∴ △CBF≌△CBD.∴ CF=CD.∴ CD=2CE.
典例4图答案
类型3 构造中位线
方法指导:(1) 当题目中已知三角形两边的中点时,可尝试连接这两点,利用三角形的中位线定理解题;(2) 当题目中已知三角形一边的中点时,可尝试取另一边的中点,或过此中点作另一条边的平行线,构造三角形的中位线解题;(3) 当题目中存在有公共端点的线段及它们的中点时,可通过补形构造三角形的中位线解题.
典例5 如图,在Rt△ABC中,∠C=90°,E为AB的中点,点D在边BC上,∠BDE=30°.求证:DE=AC.
解:如图,过点E作 EF⊥BD,交BD于点F,则∠EFD=90°.∵ ∠BDE=30°,∴ DE=2EF.∵ ∠C=90°,∠EFD=90°,∴ ∠C+∠EFD=180°.∴ EF∥AC.又∵ E为AB的中点,∴ EF是△ABC的中位线.∴ AC=2EF.∴ DE=AC.
典例5图答案
典例6 如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC为斜边,向△ABC的内侧作等腰直角三角形ABE和等腰直角三角形ACD,M是BC的中点,连接MD,ME.求证:AB-AC=2DM.
解:如图,延长CD交AB于点F.在△ADF和△ADC中,
∵ ∴ △ADF≌△ADC.∴ AF=AC,DF=DC.又∵ M是BC的中点,∴ DM是△CBF的中位线.∴ DM=BF=(AB-AF)=(AB-AC).∴ AB-AC=2DM.
典例6图答案
强化练习
1. 如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB的中点,连接DF并延长,交AC于点E.若AB=6,BC=10,则线段EF的长为( B )
A. 1 B. 2 C. 3 D. 4
第1题
B
1
2
3
4
5
6
7
2. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,连接EF,DE.若EF=2,则DE的长为( B )
A. 2 B. 1
C. D. +1
第2题
B
1
2
3
4
5
6
7
3. (2023·滁州凤阳二模)如图,在矩形ABCD中,AB=6,AD=8,AE平分∠BAD交BC于点E.F,G分别是AD,AE的中点,则FG的长为( B )
A. 3 B.
C. 4 D. 5
第3题
B
1
2
3
4
5
6
7
4. (2023·合肥蜀山二模)如图,在△ABC中,∠ACB=90°,角平分线BE与中线CD交于点F.若AC=16,BC=12,则的值为( B )
A. B.
C. D.
第4题
B
1
2
3
4
5
6
7
5. 如图,在△ABC中,AB=12,AC=5,AD是∠BAC的平分线,AE是边BC上的中线,过点C作CF⊥AD于点F,连接EF,则EF的长为 3.5 .
第5题
3.5
1
2
3
4
5
6
7
6. 在△ABC中,∠C=60°,D是边AB的中点,E是边BC上一点,连接DE,DE=2.
(1) 若E是BC的中点,则AC= 4 .
(2) 若DE平分△ABC的周长,则AC= .
4
1
2
3
4
5
6
7
7. 如图,在Rt△ABC中,∠B=90°,∠C=45°,D为边AC的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,连接EF.若AE=8,FC=6,求EF的长.
1
2
3
4
5
6
7
解:如图,连接BD.∵ ∠ABC=90°,∠C=45°,∴ ∠A=90°-∠C=45°.∴ ∠C=∠A.∴ AB=BC.∵ D为边AC的中点,∴ ∠ABD=∠CBD=45°,BD=AD=CD,BD⊥AC.∴ ∠EBD=∠C.∵ ∠EDB+∠FDB=90°,∠FDB+∠CDF=90°,∴ ∠EDB=∠FDC.在△BED和△CFD中,∵ ∴ △BED≌△CFD.∴ BE=CF=6.∵ AB=BC,∴ AB-BE=BC-CF,即AE=BF=8.在Rt△BEF中,EF==10
第7题答案
1
2
3
4
5
6
7
与中点有关的辅助线问题
类型1 构造中线
方法指导:(1) 当题目中已知直角三角形与斜边的中点时,可尝试连接直角顶点与斜边的中点,利用“直角三角形斜边上的中线等于斜边的一半”解题;(2) 当题目中已知等腰三角形与底边的中点时,可连接等腰三角形的顶角顶点与底边的中点,利用“三线合一”解题.
典例1 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,则CE的长为( C )
典例1图
A. 2 B. 4 C. 6 D. 8
C
典例2 如图,在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=CD.求∠BAC的度数.
解:如图,取线段CD的中点E,连接AE.∵ ∠DAC=90°,∴ AE=CE=DE=CD.∴ ∠CAE=∠C.∵ ∠C=25°,∴ ∠CAE=25°.∴ ∠AEB=∠CAE+∠C=50°.∵ AB=CD,∴ AB=AE.∴ ∠B=∠AEB=50°.
∵ ∠B+∠C+∠BAC=180°,∴ 50°+25°+∠BAC=180°.∴ ∠BAC=105°.
典例2图答案
类型2倍长中线
方法指导:当题目中已知三角形一边上的中线时,可尝试将此中线延长至它的一倍,构造全等三角形,利用全等三角形的性质解题.
典例3 如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长,交AC于点E.若AE=EF,求证:AC=BF.
典例3图答案
解:如图,延长AD至点H,使DH=AD,连接BH.∵ AD是△ABC的中线,∴ CD=BD.又∵ ∠ADC=∠HDB,AD=HD,
∴ △ADC≌△HDB.∴ AC=HB,∠CAD=∠H.∵ AE=EF,∴ ∠EAF=∠AFE.∴ ∠H=∠AFE.又∵ ∠AFE=∠BFH,∴ ∠H=∠BFH.∴ BF=BH.∴ AC=BF.
典例4 如图,CE,CB分别是△ABC,△ADC的中线,且AB=AC.求证:CD=2CE.
解:如图,延长CE到点F,使EF=CE,连接BF,则CF=2CE.∵ CE是△ABC的中线,∴ BE=AE.在△BEF和△AEC中,
∵ ∴ △BEF≌△AEC.∴ ∠EBF=∠A,BF=AC.∵ AB=AC,∴ ∠ABC=∠ACB.∴ ∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.∵ CB是△ADC的中线,∴ AB=BD.又∵ AB=AC,AC=BF,∴ AB=BF.∴ BF=BD.在△CBF和△CBD中,
∵ ∴ △CBF≌△CBD.∴ CF=CD.∴ CD=2CE.
典例4图答案
类型3 构造中位线
方法指导:(1) 当题目中已知三角形两边的中点时,可尝试连接这两点,利用三角形的中位线定理解题;(2) 当题目中已知三角形一边的中点时,可尝试取另一边的中点,或过此中点作另一条边的平行线,构造三角形的中位线解题;(3) 当题目中存在有公共端点的线段及它们的中点时,可通过补形构造三角形的中位线解题.
典例5 如图,在Rt△ABC中,∠C=90°,E为AB的中点,点D在边BC上,∠BDE=30°.求证:DE=AC.
解:如图,过点E作 EF⊥BD,交BD于点F,则∠EFD=90°.∵ ∠BDE=30°,∴ DE=2EF.∵ ∠C=90°,∠EFD=90°,∴ ∠C+∠EFD=180°.∴ EF∥AC.又∵ E为AB的中点,∴ EF是△ABC的中位线.∴ AC=2EF.∴ DE=AC.
典例5图答案
典例6 如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC为斜边,向△ABC的内侧作等腰直角三角形ABE和等腰直角三角形ACD,M是BC的中点,连接MD,ME.求证:AB-AC=2DM.
解:如图,延长CD交AB于点F.在△ADF和△ADC中,
∵ ∴ △ADF≌△ADC.∴ AF=AC,DF=DC.又∵ M是BC的中点,∴ DM是△CBF的中位线.∴ DM=BF=(AB-AF)=(AB-AC).∴ AB-AC=2DM.
典例6图答案
强化练习
1. 如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB的中点,连接DF并延长,交AC于点E.若AB=6,BC=10,则线段EF的长为( B )
A. 1 B. 2 C. 3 D. 4
第1题
B
1
2
3
4
5
6
7
2. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,连接EF,DE.若EF=2,则DE的长为( B )
A. 2 B. 1
C. D. +1
第2题
B
1
2
3
4
5
6
7
3. (2023·滁州凤阳二模)如图,在矩形ABCD中,AB=6,AD=8,AE平分∠BAD交BC于点E.F,G分别是AD,AE的中点,则FG的长为( B )
A. 3 B.
C. 4 D. 5
第3题
B
1
2
3
4
5
6
7
4. (2023·合肥蜀山二模)如图,在△ABC中,∠ACB=90°,角平分线BE与中线CD交于点F.若AC=16,BC=12,则的值为( B )
A. B.
C. D.
第4题
B
1
2
3
4
5
6
7
5. 如图,在△ABC中,AB=12,AC=5,AD是∠BAC的平分线,AE是边BC上的中线,过点C作CF⊥AD于点F,连接EF,则EF的长为 3.5 .
第5题
3.5
1
2
3
4
5
6
7
6. 在△ABC中,∠C=60°,D是边AB的中点,E是边BC上一点,连接DE,DE=2.
(1) 若E是BC的中点,则AC= 4 .
(2) 若DE平分△ABC的周长,则AC= .
4
1
2
3
4
5
6
7
7. 如图,在Rt△ABC中,∠B=90°,∠C=45°,D为边AC的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,连接EF.若AE=8,FC=6,求EF的长.
1
2
3
4
5
6
7
解:如图,连接BD.∵ ∠ABC=90°,∠C=45°,∴ ∠A=90°-∠C=45°.∴ ∠C=∠A.∴ AB=BC.∵ D为边AC的中点,∴ ∠ABD=∠CBD=45°,BD=AD=CD,BD⊥AC.∴ ∠EBD=∠C.∵ ∠EDB+∠FDB=90°,∠FDB+∠CDF=90°,∴ ∠EDB=∠FDC.在△BED和△CFD中,∵ ∴ △BED≌△CFD.∴ BE=CF=6.∵ AB=BC,∴ AB-BE=BC-CF,即AE=BF=8.在Rt△BEF中,EF==10
第7题答案
1
2
3
4
5
6
7
同课章节目录
