2024年中考数学二轮复习题型突破课件:正方形中的常考题型(共24张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:正方形中的常考题型(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 914.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:42:53 | ||
图片预览





文档简介
(共24张PPT)
正方形中的常考题型
类型1 求最值
方法指导:在已知正方形的条件下,求动点运动时,相关线段或线段和差的最大值或最小值,关键是动中求静、变中找不变,利用正方形的对称性将其转化为“垂线段最短”“两点之间线段最短”求解.两点之间线段最短,即三角形的两边之和大于第三边(两边重合时取最值).
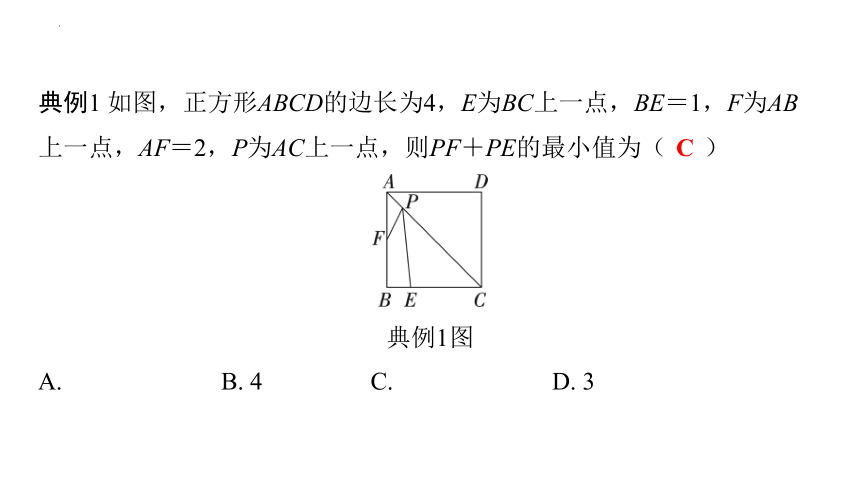
典例1 如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为( C )
典例1图
A. B. 4 C. D. 3
C
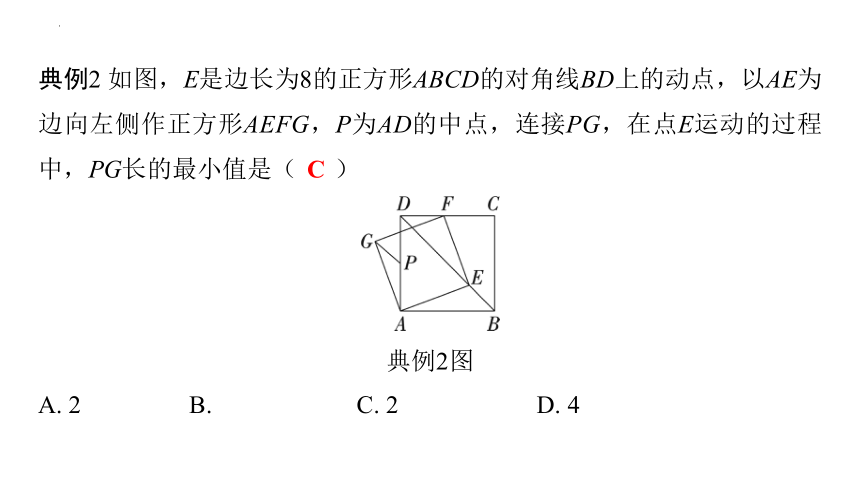
典例2 如图,E是边长为8的正方形ABCD的对角线BD上的动点,以AE为边向左侧作正方形AEFG,P为AD的中点,连接PG,在点E运动的过程中,PG长的最小值是( C )
典例2图
A. 2 B. C. 2 D. 4
C
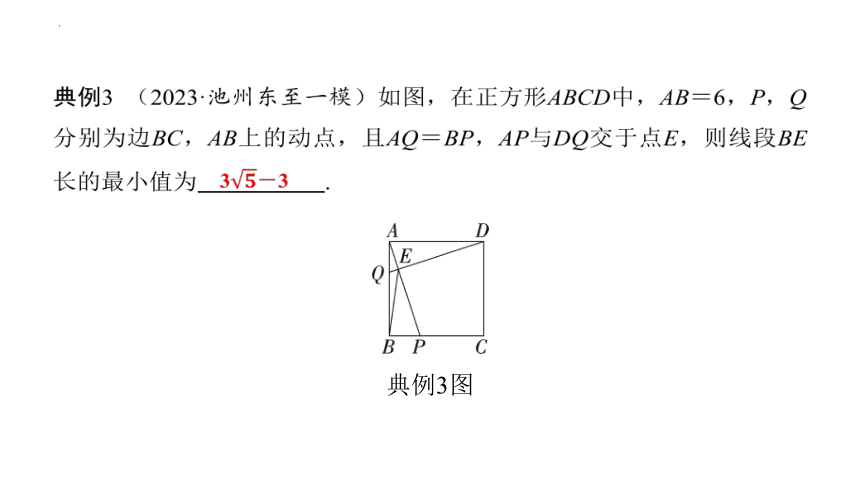
典例3 (2023·池州东至一模)如图,在正方形ABCD中,AB=6,P,Q分别为边BC,AB上的动点,且AQ=BP,AP与DQ交于点E,则线段BE长的最小值为 3-3 .
典例3图
3-3
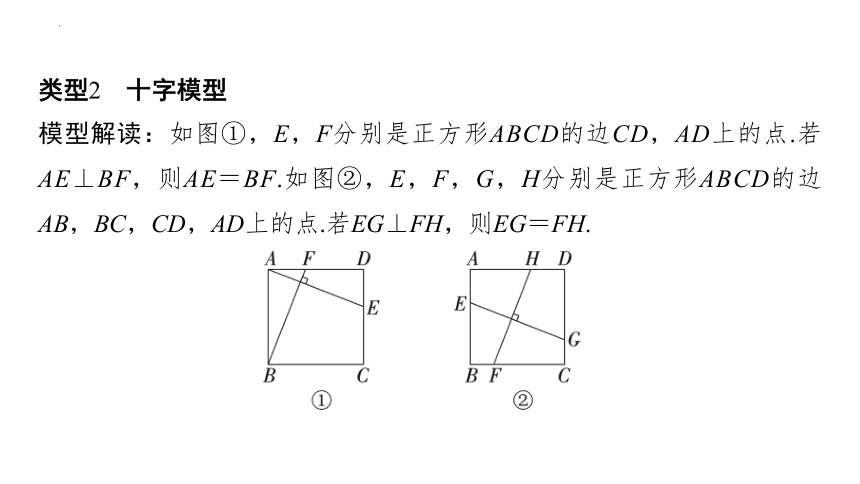
类型2 十字模型
模型解读:如图①,E,F分别是正方形ABCD的边CD,AD上的点.若AE⊥BF,则AE=BF.如图②,E,F,G,H分别是正方形ABCD的边AB,BC,CD,AD上的点.若EG⊥FH,则EG=FH.
典例4 如图,在正方形ABCD中,AE=BF,则下列结论中,一定成立的是( D )
典例4图
D
A. ∠BEC=60°
B. ∠CFD=60°
C. AB=2AE
D. CE⊥DF
典例5 如图,正方形ABCD的边长为4,E为边DC上一点,DE=3,连接AE,过点D作AE的垂线,交AE于点F,交BC于点G,则FG的长为( B )
典例5图
A. B.
C. 3 D. 5
B
典例6 如图,在正方形ABCD中,E,F分别是边BC,CD上的点,点P,Q分别在边AB,AD上,连接PF,QE交于点H,∠FHE=90°,PF=4.求QE的长.
解:如图,过点Q作QM⊥BC于点M,过点P作PN⊥CD于点N.∵ 四边形ABCD是正方形,∴ ∠A=∠B=∠C=90°.∵ QM⊥BC,∴ ∠QMB=∠B=∠A=90°.∴ 四边形ABMQ是矩形.∴ AB=QM.同理,可得四边形BCNP是矩形.∴ BC=PN,PN∥BC.∴ QM⊥PN.∵ 四边形ABCD是正方形,∴ AB=BC.∴ QM=PN.∵ ∠FHE=90°,∴ PF⊥QE.∴ 易知∠MQE=∠NPF.在△QME和△PNF中,
∵ ∴ △QME≌△PNF.∴ QE=PF=4.
典例6图答案
类型3 对角互补模型
模型解读:如图①,若∠ABC=∠ADC=90°,AD=CD,如图②,过点D 作DE⊥BA于点E,DF⊥BC于点F,则△DEA≌△DFC,AB+BC=2BF=BD.
典例7 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,则AF的长是( B )
典例7图
A. 2 B. C. D.
B
典例8 如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.
典例8图
解:∵ 四边形ABCD为正方形,∴ OC=OD,∠OCE=∠ODF=45°,AC⊥BD.∴ ∠COD=90°.∴ ∠DOF+∠COF=90°.∵ ∠EOF=90°,
∴ ∠COE+∠COF=90°.∴ ∠COE=∠DOF.∴ △COE≌△DOF.∴ CE=DF.
类型4 半角模型
模型解读:如图,在正方形ABCD中,∠EAF=45°,延长CB到点G,使BG=DF,连接EF,AG,则△AEF≌△AEG,EF=EG=BE+DF.
典例9 如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=GF.
典例9图
解:∵ 四边形ABCD是正方形,∴ AB=AD,∠B=∠BAD=∠ADC=90°.∵ 点G在CD的延长线上,∴ ∠ADG=180°-∠ADC=90°.∴ ∠B=∠ADG.在△ABE和△ADG中,∵ ∴ △ABE≌△ADG.
∴ ∠BAE=∠DAG,AE=AG.∵ ∠EAF=45°,∴ ∠BAE+∠DAF=45°.∴ ∠DAG+∠DAF=45°,即∠GAF=45°.在△EAF和△GAF中,
∵ ∴ △EAF≌△GAF.∴ EF=GF.
典例9图
强化练习
1. (2023·芜湖一模)如图,在正方形ABCD中,AB=5,E是边BC上一动点(点E不与点B,C重合),连接AE,作点B关于直线AE的对称点F,连接CF,则CF长的最小值为( B )
A. 5 B. 5-5
C. D.
第1题
B
1
2
3
4
5
6
2. (2023·合肥模拟)如图,在△BCP中,BP=,PC=4,现以BC为边在BC下方作正方形ABCD并连接AP,则AP长的最大值为( B )
A. 2 B. 6
C. 4+2 D.
第2题
B
1
2
3
4
5
6
3. 如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( D )
A. 2 B. C. D.
第3题
D
1
2
3
4
5
6
4. 如图,正方形ABCD的边长为4,点E,F分别在AB,AD上.若CE=2,且∠ECF=45°,则CF的长为( A )
A. B. C. 2 D.
第4题
A
1
2
3
4
5
6
5. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF= .
第5题
1
2
3
4
5
6
6. 操作发现:在正方形ABCD中,P是对角线AC和BD的交点,∠EPF=90°,∠EPF的两边分别交直线AB,BC于点E,F.
(1) 当点E,F分别在边AB,BC上时,如图①,求证:(AE+CF)=AC.
解:(1) ∵ 四边形ABCD是正方形,∴ AB=BC,AC=BD,AP=AC,BP=BD,∠ABC=90°,∠PAE=∠PBF=45°,∠APB=90°.
∴ AP=BP.又∵ ∠EPF=90°,∴ ∠APB=∠EPF.∴ ∠APB-∠EPB=∠EPF-∠EPB,即∠APE=∠BPF.∴ △APE≌△BPF.∴ AE=BF.
∵ 在Rt△ABC中,∠ABC=90°,AB=BC,∴ 由勾股定理,得AC==BC.又∵ BC=BF+CF=AE+CF,∴ (AE+CF)=AC
第6题
1
2
3
4
5
6
(2) 当点E,F分别在边BA,CB的延长线上时,如图②,线段AE,CF,AC之间的数量关系是 (CF-AE)=AC .
(3) 当点E,F分别在边AB,BC的延长线上时,如图③,线段AE,CF,AC之间的数量关系是 (AE-CF)=AC .
第6题
(AE-CF)=AC
(CF-AE)=AC
1
2
3
4
5
6
正方形中的常考题型
类型1 求最值
方法指导:在已知正方形的条件下,求动点运动时,相关线段或线段和差的最大值或最小值,关键是动中求静、变中找不变,利用正方形的对称性将其转化为“垂线段最短”“两点之间线段最短”求解.两点之间线段最短,即三角形的两边之和大于第三边(两边重合时取最值).
典例1 如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为( C )
典例1图
A. B. 4 C. D. 3
C
典例2 如图,E是边长为8的正方形ABCD的对角线BD上的动点,以AE为边向左侧作正方形AEFG,P为AD的中点,连接PG,在点E运动的过程中,PG长的最小值是( C )
典例2图
A. 2 B. C. 2 D. 4
C
典例3 (2023·池州东至一模)如图,在正方形ABCD中,AB=6,P,Q分别为边BC,AB上的动点,且AQ=BP,AP与DQ交于点E,则线段BE长的最小值为 3-3 .
典例3图
3-3
类型2 十字模型
模型解读:如图①,E,F分别是正方形ABCD的边CD,AD上的点.若AE⊥BF,则AE=BF.如图②,E,F,G,H分别是正方形ABCD的边AB,BC,CD,AD上的点.若EG⊥FH,则EG=FH.
典例4 如图,在正方形ABCD中,AE=BF,则下列结论中,一定成立的是( D )
典例4图
D
A. ∠BEC=60°
B. ∠CFD=60°
C. AB=2AE
D. CE⊥DF
典例5 如图,正方形ABCD的边长为4,E为边DC上一点,DE=3,连接AE,过点D作AE的垂线,交AE于点F,交BC于点G,则FG的长为( B )
典例5图
A. B.
C. 3 D. 5
B
典例6 如图,在正方形ABCD中,E,F分别是边BC,CD上的点,点P,Q分别在边AB,AD上,连接PF,QE交于点H,∠FHE=90°,PF=4.求QE的长.
解:如图,过点Q作QM⊥BC于点M,过点P作PN⊥CD于点N.∵ 四边形ABCD是正方形,∴ ∠A=∠B=∠C=90°.∵ QM⊥BC,∴ ∠QMB=∠B=∠A=90°.∴ 四边形ABMQ是矩形.∴ AB=QM.同理,可得四边形BCNP是矩形.∴ BC=PN,PN∥BC.∴ QM⊥PN.∵ 四边形ABCD是正方形,∴ AB=BC.∴ QM=PN.∵ ∠FHE=90°,∴ PF⊥QE.∴ 易知∠MQE=∠NPF.在△QME和△PNF中,
∵ ∴ △QME≌△PNF.∴ QE=PF=4.
典例6图答案
类型3 对角互补模型
模型解读:如图①,若∠ABC=∠ADC=90°,AD=CD,如图②,过点D 作DE⊥BA于点E,DF⊥BC于点F,则△DEA≌△DFC,AB+BC=2BF=BD.
典例7 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,则AF的长是( B )
典例7图
A. 2 B. C. D.
B
典例8 如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.
典例8图
解:∵ 四边形ABCD为正方形,∴ OC=OD,∠OCE=∠ODF=45°,AC⊥BD.∴ ∠COD=90°.∴ ∠DOF+∠COF=90°.∵ ∠EOF=90°,
∴ ∠COE+∠COF=90°.∴ ∠COE=∠DOF.∴ △COE≌△DOF.∴ CE=DF.
类型4 半角模型
模型解读:如图,在正方形ABCD中,∠EAF=45°,延长CB到点G,使BG=DF,连接EF,AG,则△AEF≌△AEG,EF=EG=BE+DF.
典例9 如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=GF.
典例9图
解:∵ 四边形ABCD是正方形,∴ AB=AD,∠B=∠BAD=∠ADC=90°.∵ 点G在CD的延长线上,∴ ∠ADG=180°-∠ADC=90°.∴ ∠B=∠ADG.在△ABE和△ADG中,∵ ∴ △ABE≌△ADG.
∴ ∠BAE=∠DAG,AE=AG.∵ ∠EAF=45°,∴ ∠BAE+∠DAF=45°.∴ ∠DAG+∠DAF=45°,即∠GAF=45°.在△EAF和△GAF中,
∵ ∴ △EAF≌△GAF.∴ EF=GF.
典例9图
强化练习
1. (2023·芜湖一模)如图,在正方形ABCD中,AB=5,E是边BC上一动点(点E不与点B,C重合),连接AE,作点B关于直线AE的对称点F,连接CF,则CF长的最小值为( B )
A. 5 B. 5-5
C. D.
第1题
B
1
2
3
4
5
6
2. (2023·合肥模拟)如图,在△BCP中,BP=,PC=4,现以BC为边在BC下方作正方形ABCD并连接AP,则AP长的最大值为( B )
A. 2 B. 6
C. 4+2 D.
第2题
B
1
2
3
4
5
6
3. 如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( D )
A. 2 B. C. D.
第3题
D
1
2
3
4
5
6
4. 如图,正方形ABCD的边长为4,点E,F分别在AB,AD上.若CE=2,且∠ECF=45°,则CF的长为( A )
A. B. C. 2 D.
第4题
A
1
2
3
4
5
6
5. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF= .
第5题
1
2
3
4
5
6
6. 操作发现:在正方形ABCD中,P是对角线AC和BD的交点,∠EPF=90°,∠EPF的两边分别交直线AB,BC于点E,F.
(1) 当点E,F分别在边AB,BC上时,如图①,求证:(AE+CF)=AC.
解:(1) ∵ 四边形ABCD是正方形,∴ AB=BC,AC=BD,AP=AC,BP=BD,∠ABC=90°,∠PAE=∠PBF=45°,∠APB=90°.
∴ AP=BP.又∵ ∠EPF=90°,∴ ∠APB=∠EPF.∴ ∠APB-∠EPB=∠EPF-∠EPB,即∠APE=∠BPF.∴ △APE≌△BPF.∴ AE=BF.
∵ 在Rt△ABC中,∠ABC=90°,AB=BC,∴ 由勾股定理,得AC==BC.又∵ BC=BF+CF=AE+CF,∴ (AE+CF)=AC
第6题
1
2
3
4
5
6
(2) 当点E,F分别在边BA,CB的延长线上时,如图②,线段AE,CF,AC之间的数量关系是 (CF-AE)=AC .
(3) 当点E,F分别在边AB,BC的延长线上时,如图③,线段AE,CF,AC之间的数量关系是 (AE-CF)=AC .
第6题
(AE-CF)=AC
(CF-AE)=AC
1
2
3
4
5
6
同课章节目录
