2024年中考数学二轮复习突破课件:专题二 几何最值问题(共62张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习突破课件:专题二 几何最值问题(共62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览








文档简介
(共62张PPT)
专题二 几何最值问题
类型1 由垂线段最短求最值
模型1:“一动一定”型(一个动点+一个定点)
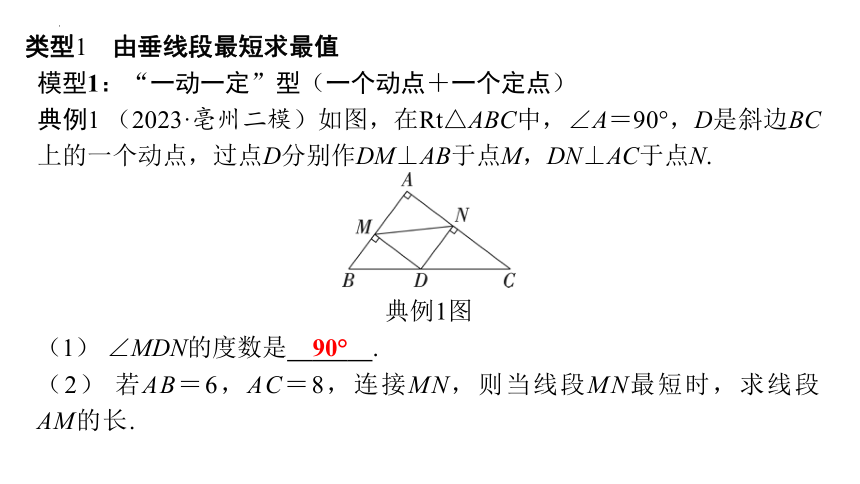
典例1 (2023·亳州二模)如图,在Rt△ABC中,∠A=90°,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
典例1图
(1) ∠MDN的度数是 90° .
(2) 若AB=6,AC=8,连接MN,则当线段MN最短时,求线段AM的长.
90°
[思路点拨] (1) 根据有三个直角的四边形是矩形,可证得四边形DMAN是矩形,因此∠MDN=90°.(2) 连接AD,根据矩形的对角线相等,可知AD=MN.当线段MN最短时,线段AD也最短,因此当AD⊥BC时,AD最短,此时MN最短.结合等面积法与相似三角形可求得此时线段AM的长.
解:如图,连接AD.∵ ∠BAC=90°,AB=6,AC=8,∴ BC==10.∵ DM⊥AB,DN⊥AC,∴ ∠DMA=∠DNA=90°.又∵ ∠BAC=90°,四边形DMAN是矩形,∴ MN=AD.当AD⊥BC时,线段AD最短,即线段MN最短,此时S△ABC=AB·AC=BC·AD.∴ AD==.∵ ∠AMD=∠ADB=90°,∠MAD=∠DAB,
∴ △ADM∽△ABD.∴ =.∴ =.∴ AM=.
典例1图答案
典例1图
跟踪训练
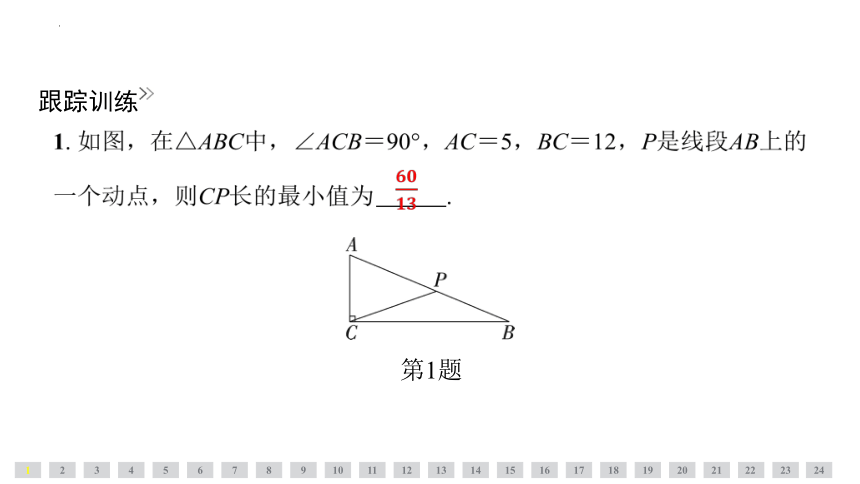
1. 如图,在△ABC中,∠ACB=90°,AC=5,BC=12,P是线段AB上的一个动点,则CP长的最小值为 .
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
模型2:“两动一定”型(两个动点+一个定点)
典例2 (2023·池州贵池模拟)如图,在Rt△ABC中,∠ACB=90°,BC=6,∠B=30°,动点M,N分别在边AB,BC上,则CM+MN的最小值是( D )
典例2图
D
A. 2
B. 2
C. 6
D. 3
[思路点拨] 作点C关于AB的对称点E,连接EB,EM,EN,过点E作EF⊥BC于点F.先根据轴对称将CM+MN转化为EM+MN,再根据两点之间线段最短和垂线段最短,可知EM+MN≥EN≥EF,故CM+MN的最小值为EF的长,结合三角函数求出EF的长即可.
跟踪训练
2. (2023·合肥模拟)如图,在四边形ABCD中,∠ABC=60°,BC=2+2,BD平分∠ABC.若P,Q分别是BD,BC上的动点,则CP+PQ的最小值是( B )
A. 2+2
B. +3
C. 2+2
D. +4
第2题
B
类型2 利用“两点之间,线段最短”求最值
模型1:“一线两定”型(一个动点+两个定点)
(1) 异侧线段和的最小值问题
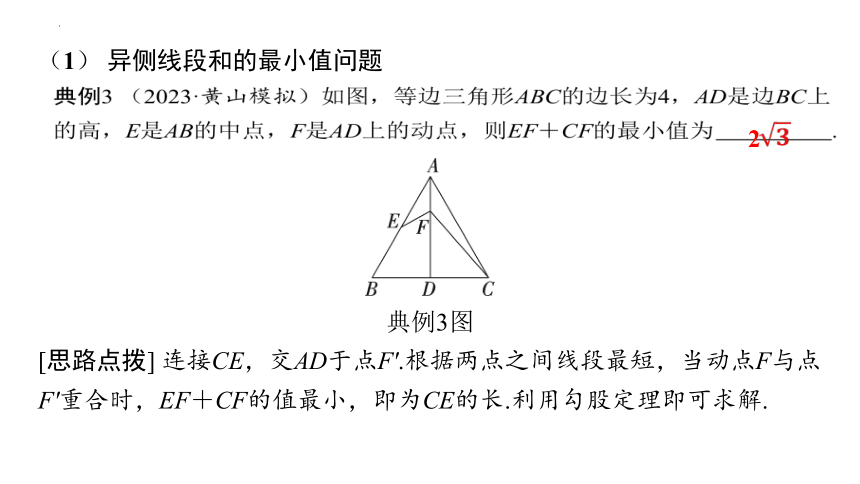
典例3 (2023·黄山模拟)如图,等边三角形ABC的边长为4,AD是边BC上的高,E是AB的中点,F是AD上的动点,则EF+CF的最小值为 2 .
典例3图
[思路点拨] 连接CE,交AD于点F'.根据两点之间线段最短,当动点F与点F'重合时,EF+CF的值最小,即为CE的长.利用勾股定理即可求解.
2
跟踪训练
3. (2023·阜阳太和一模)如图,P是矩形ABCD内的任意一点,连接PA,PB,PC,PD,得到△PAD,△PAB,△PBC,△PCD,设它们的面积分别是S1,S2,S3,S4,则下列结论中,错误的是( D )
A. 若S1=S3,则点P在AB的垂直平分线上
B. S2+S4=S1+S3
C. 若AB=4,BC=3,则PA+PB+PC+PD的最小值为10
D. 若△PAB∽△PDA,且AB=4,BC=3,则PA=2.5
第3题
D
(2) 同侧线段和最小值问题(将军饮马)
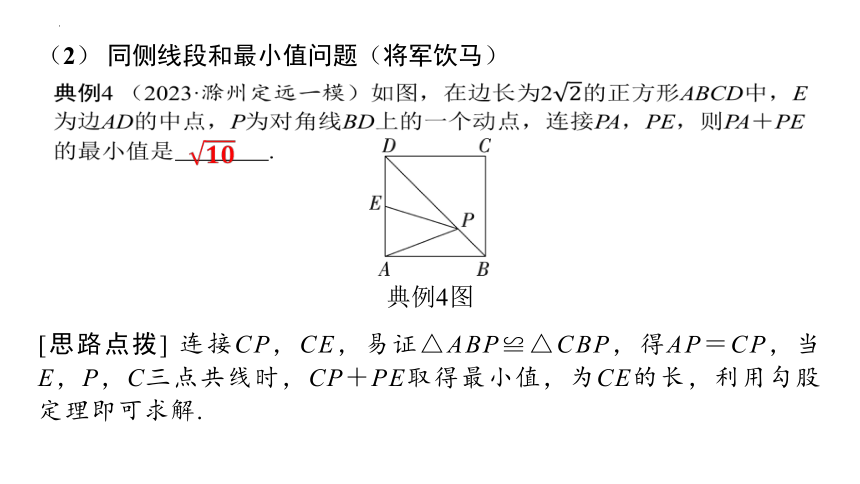
典例4 (2023·滁州定远一模)如图,在边长为2的正方形ABCD中,E为边AD的中点,P为对角线BD上的一个动点,连接PA,PE,则PA+PE的最小值是 .
典例4图
[思路点拨] 连接CP,CE,易证△ABP≌△CBP,得AP=CP,当E,P,C三点共线时,CP+PE取得最小值,为CE的长,利用勾股定理即可求解.
跟踪训练
4. (2023·马鞍山模拟)如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上运动.当PA+PD取得最小值时,△APD的边AP上的高为( B )
A.
B.
C.
D.
第4题
B
模型2:“一点两线”型(两个动点+一个定点)
典例5 如图,∠AOB=30°,M,N分别为射线OA,OB上的动点,P为∠AOB内一点,连接OP,PM,PN,MN.若OP=5,则△PMN的周长的最小值为 5 .
典例5图
[思路点拨] 分别作点P关于OA,OB的对称点C,D,连接CD,分别交OA,OB于点M,N,此时△PMN的周长取得最小值.结合轴对称即可求出△PMN的周长的最小值.
5
跟踪训练
5. 如图,在四边形ABCD中,∠A=∠C=90°,∠B=34°,在边AB,BC上分别找一点E,F,使△DEF的周长最小,此时∠EDF的度数为 112° .
第5题
112°
类型3 圆中的最值问题(含“隐”圆)
模型1:点和圆的最值问题
典例6 (2023·安庆岳西模拟)如图,E是边长为4的正方形ABCD的边CD上的一个动点,F是以BC为直径的半圆O上的一个动点,连接AE,EF,求AE+EF的最小值.
[思路点拨] 延长AD到点G,使得AD=DG,连接OG,交CD于点M,交半圆于点N,则AE+EF的最小值即为GN的长,根据GN=OG-ON并结合勾股定理即可求解.
解:如图,延长AD到点G,使得AD=DG,连接OG交CD于点M,交半圆O于点N,则AE+EF的最小值即为GN的长.由题意,得AD=DG=BC=4,ON=OC=BC=2.过点O作OH⊥AD于点H,则∠OHG=90°.
又∵ ∠ADC=∠DCB=90°.∴ 四边形OCDH是矩形.∴ OH=CD=4,DH=OC=2.∴ OG==2.∴ AE+EF的最小值为OG-ON=2-2.
典例6图答案
跟踪训练
6. (2022·泸州)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,半径为1的☉O在Rt△ABC内平移(☉O可以与该三角形的边相切),则点A到☉O上的点的距离的最大值为 2+1 .
第6题
2+1
模型2:线和圆的最值问题
典例7 如图,等边三角形ABC的边长为4,☉C的半径为,P为边AB上一动点,过点P作☉C的切线PQ,切点为Q,则PQ长的最小值为( D )
典例7图
D
A.
B.
C. 2
D. 3
[思路点拨] 连接CQ,CP,过点C作CH⊥AB于点H,根据切线的性质得到CQ⊥PQ,根据勾股定理可知PQ=.当CP⊥AB,即点P与点H重合时,CP的长最小,此时PQ的长取得最小值.
跟踪训练
7. 如图,在平面直角坐标系中,☉P经过点A(8,0),O(0,0),B(0,6).若D是☉P上的一动点,则当点D到弦OB的距离最大时,sin∠BOD的值是( D )
A.
B. 3
C.
D.
第7题
D
模型3:定点定长构造辅助圆求最值
典例8 如图,在等边三角形ABC和等边三角形ADE中,N,M分别为BC,DE的中点,连接MN,AB=6,AD=4.在△ADE绕点A旋转的过程中,MN长的最大值为 5 .
典例8图
5
[思路点拨] 连接AN,AM,以点A为圆心、AM长为半径作圆,延长NA,与圆交于点M',点M在以点A为圆心、AM长为半径的圆上运动,则MN长的最大值为M'N的长,根据勾股定理分别算出AM,AN的长,则MN长的最大值为M'N=AN+AM'=AN+AM.
跟踪训练
8. 如图,点A,B的坐标分别为(4,0),(0,4),C为平面内一点,BC=2,M为线段AC的中点,连接OM,则OM长的最大值为 1+2 .
第8题
1+
2
模型4:定弦定角构造辅助圆求最值
典例9 (2023·安庆迎江三模)如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,D为线段AC上一动点,连接BD,过点C作CH⊥BD于点H,连接AH,则AH长的最小值为( D )
典例9图
D
A. 2
B. 4
C. 2-2
D. 2-2
[思路点拨] 取BC的中点G,以点G为圆心、CG长为半径作☉G,连接AG.由直角三角形的性质,可得☉G过点H,由勾股定理,可得AG=2,由AH≥AG-HG,可得当H为线段AG与☉G的交点时,AH的长取得最小值.
跟踪训练
9. (2023·合肥庐阳一模)如图,在Rt△ABC中,∠C=90°,AB=10,点P为△ABC的内心,连接AP,BP,O为AB的中点,将BO绕点B按顺时针方向旋转90°,得到线段BD,连接DP,则DP长的最小值为( A )
A. 5-5
B.
C. 3-3
D. 5-
第9题
A
模型5:利用四点共圆求最值
典例10 (2023·滁州全椒模拟)如图,在△ABC中,AB=AC=BC=4,延长BA至点D,连接CD,使得∠ADC=45°,P为边BC上一动点,过点P作PE⊥AB于点E,PF⊥CD于点F,连接EF,则EF长的最小值为( C )
典例10图
C
A. (+)
B. (+)
C. (3+)
D. (3+)
[思路点拨] 连接DP,取DP的中点M,连接ME,MF,得P,F,D,E四点在以点M为圆心的圆上,∠EMF=2∠ADC=90°,当DP⊥BC时,DP的长取得最小值,MF的长也取得最小值,同时EF的长也取得最小值.由此计算即可求解.
跟踪训练
10. 如图,在△ABC和△ACD中,∠ABC=∠ADC=45°,AC=6,求AD长的最大值.
解:∵ ∠ABC=∠ADC=45°,∴ A,C,D,B四点共圆.如图,作☉O经过A,C,D,B四点,连接AO并延长,交☉O于点D'.当点D运动到点D'处时,AD的长取得最大值.∵ ∠ADC=45°,∴ ∠AOC=2∠ADC=90°.∵ OA=OC,∴ △AOC是等腰直角三角形.∵ AC=6,∴ AO=6×=3.∴ AD'=2AO=6,即AD长的最大值为6.
第10题答案
强化练习
练习1 线段最值问题
1. 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,P为直线AB上一动点,连接PC,则线段PC长的最小值是( C )
A. 4 B. 4.5 C. 4.8 D. 5
第1题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. 如图,在△ABC中,AC=2,AB=3,BC=3.5,BC的垂直平分线MN交AB于点D,P是直线MN上的任意一点,则PA+PC的最小值是( B )
A. 2 B. 3 C. 3.5 D. 4.5
第2题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. 如图,在△ABC中,AB=3,BC=4,AC=5,P,Q分别是边BC,AC上的动点,则AP+PQ的最小值是( B )
A. 4 B. C. 5 D.
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. 如图,在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,E为边AC上的动点,F为边AB上的动点,则FE+EB的最小值是( B )
A. B. C. D.
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. 如图,在矩形ABCD中,AB=12,AD=10,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( D )
A. 22
B. 24
C. 25
D. 26
第5题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
6. 如图,在四边形ABCD中,∠B=∠D=90°,∠A=40°,M,N分别是边AB,AD上的动点.当△MCN的周长最小时,∠MCN的度数是( D )
A. 50° B. 70° C. 90° D. 100°
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. 如图,正方形ABCD的边长为3,点E在边AB上且BE=1,P,Q分别是边BC,CD上的动点(均不与顶点重合).当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( B )
A. B.
C. D.
第7题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. 如图,在矩形ABCD中,AB=6,AD=12,E为边BC上的动点,F为CD的中点,连接AE,EF,则AE+EF的最小值为 15 .
第8题
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. 如图,动点P在矩形ABCD内运动,AB=7,BC=5,且满足=10.5,则PA+PB的最小值是 .
第9题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
10. 如图,在菱形ABCD中,AC=6,BD=8,对角线AC与BD相交于点O,E是AB的中点,点M,N分别在AC,BC上,则EM+MN的最小值为 .
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
11. 如图,河的两岸有A,B两个水文观测点,为方便联络,要在河上修一座木桥MN(河的两岸互相平行,MN垂直于河岸).现测得A,B两点到河岸的距离分别是5m,4m,河宽MN为3m,且A,B两点之间的水平距离为12m,则AM+MN+NB的最小值是 18 m.
第11题
18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
12. 如图,二次函数y=-x2+x+2的图象与x轴交于A,B(点A在点B的左侧)两点,与y轴交于点C,M为直线BC上一动点,N为x轴上一动点,连接AM,MN,则AM+MN的最小值为 4 .
第12题
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13. 如图,在四边形ABCD中,AD∥BC,DC⊥BC于点C,P为BC上一动点,过点P作PQ⊥AB于点Q.若∠ABC=45°,CD=3,BC=7,则DP+PQ的最小值为 5 .
第13题
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
14. 如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,D是边AC的中点,E是直线BC上一动点,将线段DE绕点D按逆时针方向旋转90°,得到线段DF,连接AF,EF.在点E的运动过程中,求线段AF长的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
解:如图,过点D作DM⊥BC于点M,过点F作FJ⊥DM于点J,交AB于点N.∵ 在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,∴ AC=2BC=4,AB=BC=2.∵ D是AC的中点,∴ AD=DC.∵ 易得DM∥AB,∴ △CDM∽△CAB.∴ ===.∴ DM=AB=,BM=CM=BC=1.∵ 易知四边形BMJN是矩形,∴ JN=BM=1.
∵ ∠FDJ+∠EDM=90°,∠EDM+∠DEM=90°,∴ ∠FDJ=∠DEM.∵ ∠FJD=∠DME=90°,FD=DE,∴ △FJD≌△DME. ∴ FJ=DM=.∴ FN=FJ+JN=1+.∴ 点F在直线l上运动(直线l与直线AB之间的距离为+1).根据垂线段最短可知,当AF⊥直线l时,AF最短.∴ 线段AF长的最小值为+1.
第14题答案
第14题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
练习2 圆中的最值问题(含“隐”圆)
1. 在Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( D )
A. B. 1
C. -3 D. -2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,☉O的圆心O与正方形的中心重合.若☉O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点的距离的最小值为( D )
A. B. 2
C. 4+2 D. 4-2
第2题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC.若∠PBC=∠PAB,则PC长的最小值是( C )
A. 6 B. -3
C. 2-4 D. 4-4
第3题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,☉O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,C为优弧AB上的一个动点,则△ABC面积的最大值是( A )
A. 12 B. 12
C. 4 D. 8+8
第4题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,正方形ABCD的边长为2,P是射线AD上的一个动点,点Q在BP上,且满足∠BCQ=∠BPC,则线段CQ长的最小值为( C )
A. B. 1
C. -1 D. 2-1
第5题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在平面直角坐标系中,O为原点,OA=OB=3,C为平面内一动点,BC=,连接AC,M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM的长取最大值时,点M的坐标是( D )
A. B.
C. D.
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,=,在矩形内找一点P,使得∠BPE=60°,则线段PD长的最小值为( A )
A. 2-2 B. 2-4
C. 4 D. 2
第7题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,点M的坐标为(3,4),点A的坐标为(-2,0),点A与点B关于原点对称,P是平面上一点,且满足PA⊥PB,则线段PM长的最小值为 3 .
第8题
3
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 如图,☉M的半径为2,圆心M的坐标为(6,8),P是☉M上的任意一点,PA⊥PB,且PA,PB分别与x轴交于A,B两点.若点A与点B关于原点O对称,则AB长的最大值为 24 .
第9题
24
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,在Rt△ABC中,∠C=90°,CA=CB=3,点D在边BC上.将△ACD沿AD折叠,使点C落在点C'处,连接BC',则BC'长的最小值为 3-3 .
第10题
3-3
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长的最小值为 -1 .
第11题
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,AB⊥BC,AB=5,E,F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰直角三角形DEF,∠EDF=90°,连接AD,则AD长的最小值为 .
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,E是AC的中点,F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,求△BDF周长的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
解:在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,∴ AB=4.
∴ AC===2.如图,以点E为圆心、AE长为半径作圆,连接BE,交☉E于点D',当点D位于点D'的位置时,BD的长最小.∵ 将△AEF沿EF对折得到△DEF,且E是AC的中点,∴ AF=DF,AE=DE=AC=.∵ C△BDF=DF+FB+BD=AF+FB+BD=AB+BD=4+BD,∴ △BDF周长的最小值为4+BD'.过点E作EM⊥AB于点M.在Rt△EMA中,∠A=30°,AE=,∴ EM=AE=,AM=AE=.∴ BM=AB-AM=4-=.在Rt△BME中,由勾股定理,得BE===.∴ BD'=BE-ED'=-.∴ △BDF周长的最小值为4+-
第13题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
专题二 几何最值问题
类型1 由垂线段最短求最值
模型1:“一动一定”型(一个动点+一个定点)
典例1 (2023·亳州二模)如图,在Rt△ABC中,∠A=90°,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
典例1图
(1) ∠MDN的度数是 90° .
(2) 若AB=6,AC=8,连接MN,则当线段MN最短时,求线段AM的长.
90°
[思路点拨] (1) 根据有三个直角的四边形是矩形,可证得四边形DMAN是矩形,因此∠MDN=90°.(2) 连接AD,根据矩形的对角线相等,可知AD=MN.当线段MN最短时,线段AD也最短,因此当AD⊥BC时,AD最短,此时MN最短.结合等面积法与相似三角形可求得此时线段AM的长.
解:如图,连接AD.∵ ∠BAC=90°,AB=6,AC=8,∴ BC==10.∵ DM⊥AB,DN⊥AC,∴ ∠DMA=∠DNA=90°.又∵ ∠BAC=90°,四边形DMAN是矩形,∴ MN=AD.当AD⊥BC时,线段AD最短,即线段MN最短,此时S△ABC=AB·AC=BC·AD.∴ AD==.∵ ∠AMD=∠ADB=90°,∠MAD=∠DAB,
∴ △ADM∽△ABD.∴ =.∴ =.∴ AM=.
典例1图答案
典例1图
跟踪训练
1. 如图,在△ABC中,∠ACB=90°,AC=5,BC=12,P是线段AB上的一个动点,则CP长的最小值为 .
第1题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
模型2:“两动一定”型(两个动点+一个定点)
典例2 (2023·池州贵池模拟)如图,在Rt△ABC中,∠ACB=90°,BC=6,∠B=30°,动点M,N分别在边AB,BC上,则CM+MN的最小值是( D )
典例2图
D
A. 2
B. 2
C. 6
D. 3
[思路点拨] 作点C关于AB的对称点E,连接EB,EM,EN,过点E作EF⊥BC于点F.先根据轴对称将CM+MN转化为EM+MN,再根据两点之间线段最短和垂线段最短,可知EM+MN≥EN≥EF,故CM+MN的最小值为EF的长,结合三角函数求出EF的长即可.
跟踪训练
2. (2023·合肥模拟)如图,在四边形ABCD中,∠ABC=60°,BC=2+2,BD平分∠ABC.若P,Q分别是BD,BC上的动点,则CP+PQ的最小值是( B )
A. 2+2
B. +3
C. 2+2
D. +4
第2题
B
类型2 利用“两点之间,线段最短”求最值
模型1:“一线两定”型(一个动点+两个定点)
(1) 异侧线段和的最小值问题
典例3 (2023·黄山模拟)如图,等边三角形ABC的边长为4,AD是边BC上的高,E是AB的中点,F是AD上的动点,则EF+CF的最小值为 2 .
典例3图
[思路点拨] 连接CE,交AD于点F'.根据两点之间线段最短,当动点F与点F'重合时,EF+CF的值最小,即为CE的长.利用勾股定理即可求解.
2
跟踪训练
3. (2023·阜阳太和一模)如图,P是矩形ABCD内的任意一点,连接PA,PB,PC,PD,得到△PAD,△PAB,△PBC,△PCD,设它们的面积分别是S1,S2,S3,S4,则下列结论中,错误的是( D )
A. 若S1=S3,则点P在AB的垂直平分线上
B. S2+S4=S1+S3
C. 若AB=4,BC=3,则PA+PB+PC+PD的最小值为10
D. 若△PAB∽△PDA,且AB=4,BC=3,则PA=2.5
第3题
D
(2) 同侧线段和最小值问题(将军饮马)
典例4 (2023·滁州定远一模)如图,在边长为2的正方形ABCD中,E为边AD的中点,P为对角线BD上的一个动点,连接PA,PE,则PA+PE的最小值是 .
典例4图
[思路点拨] 连接CP,CE,易证△ABP≌△CBP,得AP=CP,当E,P,C三点共线时,CP+PE取得最小值,为CE的长,利用勾股定理即可求解.
跟踪训练
4. (2023·马鞍山模拟)如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上运动.当PA+PD取得最小值时,△APD的边AP上的高为( B )
A.
B.
C.
D.
第4题
B
模型2:“一点两线”型(两个动点+一个定点)
典例5 如图,∠AOB=30°,M,N分别为射线OA,OB上的动点,P为∠AOB内一点,连接OP,PM,PN,MN.若OP=5,则△PMN的周长的最小值为 5 .
典例5图
[思路点拨] 分别作点P关于OA,OB的对称点C,D,连接CD,分别交OA,OB于点M,N,此时△PMN的周长取得最小值.结合轴对称即可求出△PMN的周长的最小值.
5
跟踪训练
5. 如图,在四边形ABCD中,∠A=∠C=90°,∠B=34°,在边AB,BC上分别找一点E,F,使△DEF的周长最小,此时∠EDF的度数为 112° .
第5题
112°
类型3 圆中的最值问题(含“隐”圆)
模型1:点和圆的最值问题
典例6 (2023·安庆岳西模拟)如图,E是边长为4的正方形ABCD的边CD上的一个动点,F是以BC为直径的半圆O上的一个动点,连接AE,EF,求AE+EF的最小值.
[思路点拨] 延长AD到点G,使得AD=DG,连接OG,交CD于点M,交半圆于点N,则AE+EF的最小值即为GN的长,根据GN=OG-ON并结合勾股定理即可求解.
解:如图,延长AD到点G,使得AD=DG,连接OG交CD于点M,交半圆O于点N,则AE+EF的最小值即为GN的长.由题意,得AD=DG=BC=4,ON=OC=BC=2.过点O作OH⊥AD于点H,则∠OHG=90°.
又∵ ∠ADC=∠DCB=90°.∴ 四边形OCDH是矩形.∴ OH=CD=4,DH=OC=2.∴ OG==2.∴ AE+EF的最小值为OG-ON=2-2.
典例6图答案
跟踪训练
6. (2022·泸州)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,半径为1的☉O在Rt△ABC内平移(☉O可以与该三角形的边相切),则点A到☉O上的点的距离的最大值为 2+1 .
第6题
2+1
模型2:线和圆的最值问题
典例7 如图,等边三角形ABC的边长为4,☉C的半径为,P为边AB上一动点,过点P作☉C的切线PQ,切点为Q,则PQ长的最小值为( D )
典例7图
D
A.
B.
C. 2
D. 3
[思路点拨] 连接CQ,CP,过点C作CH⊥AB于点H,根据切线的性质得到CQ⊥PQ,根据勾股定理可知PQ=.当CP⊥AB,即点P与点H重合时,CP的长最小,此时PQ的长取得最小值.
跟踪训练
7. 如图,在平面直角坐标系中,☉P经过点A(8,0),O(0,0),B(0,6).若D是☉P上的一动点,则当点D到弦OB的距离最大时,sin∠BOD的值是( D )
A.
B. 3
C.
D.
第7题
D
模型3:定点定长构造辅助圆求最值
典例8 如图,在等边三角形ABC和等边三角形ADE中,N,M分别为BC,DE的中点,连接MN,AB=6,AD=4.在△ADE绕点A旋转的过程中,MN长的最大值为 5 .
典例8图
5
[思路点拨] 连接AN,AM,以点A为圆心、AM长为半径作圆,延长NA,与圆交于点M',点M在以点A为圆心、AM长为半径的圆上运动,则MN长的最大值为M'N的长,根据勾股定理分别算出AM,AN的长,则MN长的最大值为M'N=AN+AM'=AN+AM.
跟踪训练
8. 如图,点A,B的坐标分别为(4,0),(0,4),C为平面内一点,BC=2,M为线段AC的中点,连接OM,则OM长的最大值为 1+2 .
第8题
1+
2
模型4:定弦定角构造辅助圆求最值
典例9 (2023·安庆迎江三模)如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,D为线段AC上一动点,连接BD,过点C作CH⊥BD于点H,连接AH,则AH长的最小值为( D )
典例9图
D
A. 2
B. 4
C. 2-2
D. 2-2
[思路点拨] 取BC的中点G,以点G为圆心、CG长为半径作☉G,连接AG.由直角三角形的性质,可得☉G过点H,由勾股定理,可得AG=2,由AH≥AG-HG,可得当H为线段AG与☉G的交点时,AH的长取得最小值.
跟踪训练
9. (2023·合肥庐阳一模)如图,在Rt△ABC中,∠C=90°,AB=10,点P为△ABC的内心,连接AP,BP,O为AB的中点,将BO绕点B按顺时针方向旋转90°,得到线段BD,连接DP,则DP长的最小值为( A )
A. 5-5
B.
C. 3-3
D. 5-
第9题
A
模型5:利用四点共圆求最值
典例10 (2023·滁州全椒模拟)如图,在△ABC中,AB=AC=BC=4,延长BA至点D,连接CD,使得∠ADC=45°,P为边BC上一动点,过点P作PE⊥AB于点E,PF⊥CD于点F,连接EF,则EF长的最小值为( C )
典例10图
C
A. (+)
B. (+)
C. (3+)
D. (3+)
[思路点拨] 连接DP,取DP的中点M,连接ME,MF,得P,F,D,E四点在以点M为圆心的圆上,∠EMF=2∠ADC=90°,当DP⊥BC时,DP的长取得最小值,MF的长也取得最小值,同时EF的长也取得最小值.由此计算即可求解.
跟踪训练
10. 如图,在△ABC和△ACD中,∠ABC=∠ADC=45°,AC=6,求AD长的最大值.
解:∵ ∠ABC=∠ADC=45°,∴ A,C,D,B四点共圆.如图,作☉O经过A,C,D,B四点,连接AO并延长,交☉O于点D'.当点D运动到点D'处时,AD的长取得最大值.∵ ∠ADC=45°,∴ ∠AOC=2∠ADC=90°.∵ OA=OC,∴ △AOC是等腰直角三角形.∵ AC=6,∴ AO=6×=3.∴ AD'=2AO=6,即AD长的最大值为6.
第10题答案
强化练习
练习1 线段最值问题
1. 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,P为直线AB上一动点,连接PC,则线段PC长的最小值是( C )
A. 4 B. 4.5 C. 4.8 D. 5
第1题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. 如图,在△ABC中,AC=2,AB=3,BC=3.5,BC的垂直平分线MN交AB于点D,P是直线MN上的任意一点,则PA+PC的最小值是( B )
A. 2 B. 3 C. 3.5 D. 4.5
第2题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. 如图,在△ABC中,AB=3,BC=4,AC=5,P,Q分别是边BC,AC上的动点,则AP+PQ的最小值是( B )
A. 4 B. C. 5 D.
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. 如图,在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,E为边AC上的动点,F为边AB上的动点,则FE+EB的最小值是( B )
A. B. C. D.
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. 如图,在矩形ABCD中,AB=12,AD=10,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( D )
A. 22
B. 24
C. 25
D. 26
第5题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
6. 如图,在四边形ABCD中,∠B=∠D=90°,∠A=40°,M,N分别是边AB,AD上的动点.当△MCN的周长最小时,∠MCN的度数是( D )
A. 50° B. 70° C. 90° D. 100°
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. 如图,正方形ABCD的边长为3,点E在边AB上且BE=1,P,Q分别是边BC,CD上的动点(均不与顶点重合).当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( B )
A. B.
C. D.
第7题
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. 如图,在矩形ABCD中,AB=6,AD=12,E为边BC上的动点,F为CD的中点,连接AE,EF,则AE+EF的最小值为 15 .
第8题
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. 如图,动点P在矩形ABCD内运动,AB=7,BC=5,且满足=10.5,则PA+PB的最小值是 .
第9题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
10. 如图,在菱形ABCD中,AC=6,BD=8,对角线AC与BD相交于点O,E是AB的中点,点M,N分别在AC,BC上,则EM+MN的最小值为 .
第10题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
11. 如图,河的两岸有A,B两个水文观测点,为方便联络,要在河上修一座木桥MN(河的两岸互相平行,MN垂直于河岸).现测得A,B两点到河岸的距离分别是5m,4m,河宽MN为3m,且A,B两点之间的水平距离为12m,则AM+MN+NB的最小值是 18 m.
第11题
18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
12. 如图,二次函数y=-x2+x+2的图象与x轴交于A,B(点A在点B的左侧)两点,与y轴交于点C,M为直线BC上一动点,N为x轴上一动点,连接AM,MN,则AM+MN的最小值为 4 .
第12题
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13. 如图,在四边形ABCD中,AD∥BC,DC⊥BC于点C,P为BC上一动点,过点P作PQ⊥AB于点Q.若∠ABC=45°,CD=3,BC=7,则DP+PQ的最小值为 5 .
第13题
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
14. 如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,D是边AC的中点,E是直线BC上一动点,将线段DE绕点D按逆时针方向旋转90°,得到线段DF,连接AF,EF.在点E的运动过程中,求线段AF长的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
解:如图,过点D作DM⊥BC于点M,过点F作FJ⊥DM于点J,交AB于点N.∵ 在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,∴ AC=2BC=4,AB=BC=2.∵ D是AC的中点,∴ AD=DC.∵ 易得DM∥AB,∴ △CDM∽△CAB.∴ ===.∴ DM=AB=,BM=CM=BC=1.∵ 易知四边形BMJN是矩形,∴ JN=BM=1.
∵ ∠FDJ+∠EDM=90°,∠EDM+∠DEM=90°,∴ ∠FDJ=∠DEM.∵ ∠FJD=∠DME=90°,FD=DE,∴ △FJD≌△DME. ∴ FJ=DM=.∴ FN=FJ+JN=1+.∴ 点F在直线l上运动(直线l与直线AB之间的距离为+1).根据垂线段最短可知,当AF⊥直线l时,AF最短.∴ 线段AF长的最小值为+1.
第14题答案
第14题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
练习2 圆中的最值问题(含“隐”圆)
1. 在Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( D )
A. B. 1
C. -3 D. -2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图,☉O的圆心O与正方形的中心重合.若☉O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点的距离的最小值为( D )
A. B. 2
C. 4+2 D. 4-2
第2题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC.若∠PBC=∠PAB,则PC长的最小值是( C )
A. 6 B. -3
C. 2-4 D. 4-4
第3题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 如图,☉O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,C为优弧AB上的一个动点,则△ABC面积的最大值是( A )
A. 12 B. 12
C. 4 D. 8+8
第4题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图,正方形ABCD的边长为2,P是射线AD上的一个动点,点Q在BP上,且满足∠BCQ=∠BPC,则线段CQ长的最小值为( C )
A. B. 1
C. -1 D. 2-1
第5题
C
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 如图,在平面直角坐标系中,O为原点,OA=OB=3,C为平面内一动点,BC=,连接AC,M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM的长取最大值时,点M的坐标是( D )
A. B.
C. D.
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,=,在矩形内找一点P,使得∠BPE=60°,则线段PD长的最小值为( A )
A. 2-2 B. 2-4
C. 4 D. 2
第7题
A
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 如图,点M的坐标为(3,4),点A的坐标为(-2,0),点A与点B关于原点对称,P是平面上一点,且满足PA⊥PB,则线段PM长的最小值为 3 .
第8题
3
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 如图,☉M的半径为2,圆心M的坐标为(6,8),P是☉M上的任意一点,PA⊥PB,且PA,PB分别与x轴交于A,B两点.若点A与点B关于原点O对称,则AB长的最大值为 24 .
第9题
24
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,在Rt△ABC中,∠C=90°,CA=CB=3,点D在边BC上.将△ACD沿AD折叠,使点C落在点C'处,连接BC',则BC'长的最小值为 3-3 .
第10题
3-3
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长的最小值为 -1 .
第11题
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,AB⊥BC,AB=5,E,F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰直角三角形DEF,∠EDF=90°,连接AD,则AD长的最小值为 .
第12题
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,E是AC的中点,F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,求△BDF周长的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
解:在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,∴ AB=4.
∴ AC===2.如图,以点E为圆心、AE长为半径作圆,连接BE,交☉E于点D',当点D位于点D'的位置时,BD的长最小.∵ 将△AEF沿EF对折得到△DEF,且E是AC的中点,∴ AF=DF,AE=DE=AC=.∵ C△BDF=DF+FB+BD=AF+FB+BD=AB+BD=4+BD,∴ △BDF周长的最小值为4+BD'.过点E作EM⊥AB于点M.在Rt△EMA中,∠A=30°,AE=,∴ EM=AE=,AM=AE=.∴ BM=AB-AM=4-=.在Rt△BME中,由勾股定理,得BE===.∴ BD'=BE-ED'=-.∴ △BDF周长的最小值为4+-
第13题答案
1
2
3
4
5
6
7
8
9
10
11
12
13
同课章节目录
