6.2.1向量的加法运算分层练习(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 6.2.1向量的加法运算分层练习(含解析)--人教A版(2019)高数必修二 |

|
|
| 格式 | docx | ||
| 文件大小 | 375.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
课时作业2 向量的加法运算
基础强化
1.化简++=( )
A. B.
C. D.
2.如图ABCD是平行四边形,则向量+=( )
A. B.
C. D.
3.如图所示,在四边形ABCD中,=+,则四边形为( )
A.矩形 B.正方形
C.平行四边形 D.菱形
4.如图,正六边形ABCDEF中,++=( )
A.0 B. C. D.
5.向量(+)+(+)+化简后等于( )
A. B.
C. D.
6.(多选)给出下面四个命题,其中是真命题的是( )
A.+=0 B.+=
C.+= D.0+=0
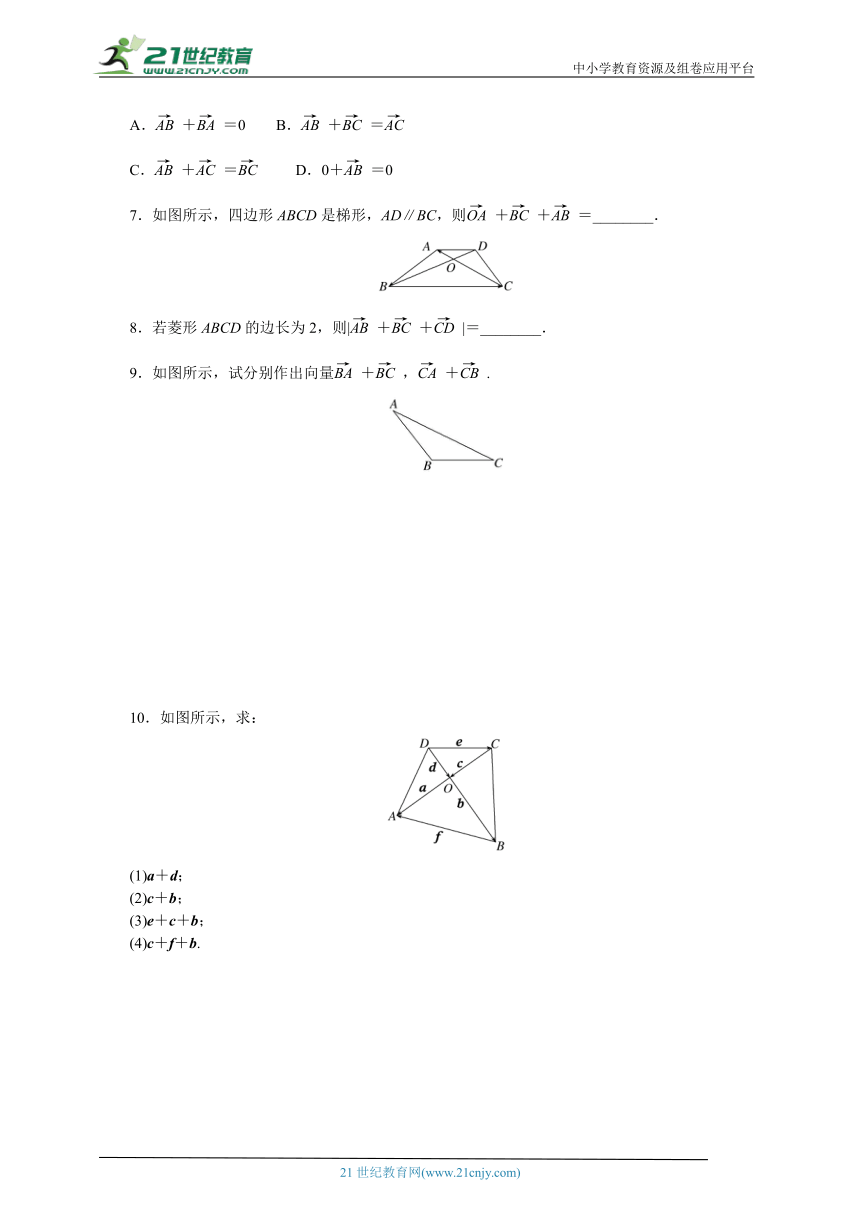
7.如图所示,四边形ABCD是梯形,AD∥BC,则++=________.
8.若菱形ABCD的边长为2,则|++|=________.
9.如图所示,试分别作出向量+,+.
10.如图所示,求:
(1)a+d;
(2)c+b;
(3)e+c+b;
(4)c+f+b.
能力提升
11.已知O是△ABC所在平面内一点,且+=,那么( )
A.点O在△ABC的内部
B.点O在△ABC的边AB上
C.点O在边AB所在的直线上
D.点O在△ABC的外部
12.若在△ABC中,=a,=b,且|a|=|b|=1,|a+b|=,则△ABC的形状是( )
A.正三角形 B.锐角三角形
C.斜三角形 D.等腰直角三角形
13.有向线段,不平行,则( )
A.|+|>||
B.|+|≥||
C.|+|≥||+||
D.|+|<||+||
14.(多选)如图,在平行四边形ABCD中,下列计算正确的是( )
A.++=
B.+=
C.++=
D.++=0
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为________.
16.在静水中船的速度是40 m/min,水流的速度是20 m/min.如果船从岸边出发,沿垂直于水流的航线到达对岸,那么船行进方向应指向何处?实际航速为多少?
课时作业2 向量的加法运算
1.解析:++=(+)+=+=.故选C.
答案:C
2.解析:因为在平行四边形ABCD中,=,所以+=+=.故选D.
答案:D
3.解析:根据平面向量的加法的平行四边形法则,若=+,
则四边形ABCD是平行四边形.故选C.
答案:C
4.解析:正六边形ABCDEF中,因为=,所以++=++=.故选B.
答案:B
5.解析:(+)+(+)+=(+)+(+)+=++=.故选C.
答案:C
6.解析:因为+=-=0,故A正确;+=,由向量加法知B正确;+=,不满足加法运算法则,故C错误;0+=,所以0+=0错误.故选AB.
答案:AB
7.解析:++=++=.
答案:
8.解析:|++|=||=2.
答案:2
9.解析:如图,以BA,BC为邻边作平行四边形ABCE,根据平行四边形法则,可知就是+.
以CB,CA为邻边作平行四边形ACBF,根据平行四边形法则,可知就是+.
所以+=,+=.
10.解析:(1)a+d=d+a=+=;
(2)c+b=+=;
(3)e+c+b=e+(c+b)=e+=+=;
(4)c+f+b=c+b+f=++=.
11.解析:因为+=,所以四边形OACB为平行四边形.从而点O在△ABC的外部.故选D.
答案:D
12.解析:由于||=|a|=1,||=|b|=1,||=|+|=|a+b|=,所以△ABC为等腰直角三角形.故选D.
答案:D
13.解析:根据向量加法的法则可知|+|与||和||的关系不确定,由向量加法的几何意义得||a|-|b||≤|a+b|≤|a|+|b|,等号当且仅当a,b共线的时候取到,而本题中,不平行,故D正确,所以本题中|+|<||+||.故选D.
答案:D
14.解析:根据向量加法运算及其几何意义,相反向量的概念,++=++=,故A错误;+=,故B正确;++=+=,故C正确;++=+=+=0,故D正确.故选BCD.
答案:BCD
15.解析:因|a|=8,|b|=12,则|a+b|≤|a|+|b|=20,当且仅当a与b同向共线时取等号,|a+b|≥|b|-|a|=4,当且仅当a与b反向共线时取等号,所以|a+b|的最大值与最小值分别为12,4.
答案:12,4
16.解析:设表示水流的速度,表示船实际航行的速度,表示船行驶的速度,
则四边形ABCD为平行四边形.所以=,∠DCA=90°,因为∠DCA=90°,于是||===20,所以∠DAC=30°,∠DAB=120°,故船的航行方向与水流方向成120°,船的实际航速为20 m/min.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业2 向量的加法运算
基础强化
1.化简++=( )
A. B.
C. D.
2.如图ABCD是平行四边形,则向量+=( )
A. B.
C. D.
3.如图所示,在四边形ABCD中,=+,则四边形为( )
A.矩形 B.正方形
C.平行四边形 D.菱形
4.如图,正六边形ABCDEF中,++=( )
A.0 B. C. D.
5.向量(+)+(+)+化简后等于( )
A. B.
C. D.
6.(多选)给出下面四个命题,其中是真命题的是( )
A.+=0 B.+=
C.+= D.0+=0
7.如图所示,四边形ABCD是梯形,AD∥BC,则++=________.
8.若菱形ABCD的边长为2,则|++|=________.
9.如图所示,试分别作出向量+,+.
10.如图所示,求:
(1)a+d;
(2)c+b;
(3)e+c+b;
(4)c+f+b.
能力提升
11.已知O是△ABC所在平面内一点,且+=,那么( )
A.点O在△ABC的内部
B.点O在△ABC的边AB上
C.点O在边AB所在的直线上
D.点O在△ABC的外部
12.若在△ABC中,=a,=b,且|a|=|b|=1,|a+b|=,则△ABC的形状是( )
A.正三角形 B.锐角三角形
C.斜三角形 D.等腰直角三角形
13.有向线段,不平行,则( )
A.|+|>||
B.|+|≥||
C.|+|≥||+||
D.|+|<||+||
14.(多选)如图,在平行四边形ABCD中,下列计算正确的是( )
A.++=
B.+=
C.++=
D.++=0
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为________.
16.在静水中船的速度是40 m/min,水流的速度是20 m/min.如果船从岸边出发,沿垂直于水流的航线到达对岸,那么船行进方向应指向何处?实际航速为多少?
课时作业2 向量的加法运算
1.解析:++=(+)+=+=.故选C.
答案:C
2.解析:因为在平行四边形ABCD中,=,所以+=+=.故选D.
答案:D
3.解析:根据平面向量的加法的平行四边形法则,若=+,
则四边形ABCD是平行四边形.故选C.
答案:C
4.解析:正六边形ABCDEF中,因为=,所以++=++=.故选B.
答案:B
5.解析:(+)+(+)+=(+)+(+)+=++=.故选C.
答案:C
6.解析:因为+=-=0,故A正确;+=,由向量加法知B正确;+=,不满足加法运算法则,故C错误;0+=,所以0+=0错误.故选AB.
答案:AB
7.解析:++=++=.
答案:
8.解析:|++|=||=2.
答案:2
9.解析:如图,以BA,BC为邻边作平行四边形ABCE,根据平行四边形法则,可知就是+.
以CB,CA为邻边作平行四边形ACBF,根据平行四边形法则,可知就是+.
所以+=,+=.
10.解析:(1)a+d=d+a=+=;
(2)c+b=+=;
(3)e+c+b=e+(c+b)=e+=+=;
(4)c+f+b=c+b+f=++=.
11.解析:因为+=,所以四边形OACB为平行四边形.从而点O在△ABC的外部.故选D.
答案:D
12.解析:由于||=|a|=1,||=|b|=1,||=|+|=|a+b|=,所以△ABC为等腰直角三角形.故选D.
答案:D
13.解析:根据向量加法的法则可知|+|与||和||的关系不确定,由向量加法的几何意义得||a|-|b||≤|a+b|≤|a|+|b|,等号当且仅当a,b共线的时候取到,而本题中,不平行,故D正确,所以本题中|+|<||+||.故选D.
答案:D
14.解析:根据向量加法运算及其几何意义,相反向量的概念,++=++=,故A错误;+=,故B正确;++=+=,故C正确;++=+=+=0,故D正确.故选BCD.
答案:BCD
15.解析:因|a|=8,|b|=12,则|a+b|≤|a|+|b|=20,当且仅当a与b同向共线时取等号,|a+b|≥|b|-|a|=4,当且仅当a与b反向共线时取等号,所以|a+b|的最大值与最小值分别为12,4.
答案:12,4
16.解析:设表示水流的速度,表示船实际航行的速度,表示船行驶的速度,
则四边形ABCD为平行四边形.所以=,∠DCA=90°,因为∠DCA=90°,于是||===20,所以∠DAC=30°,∠DAB=120°,故船的航行方向与水流方向成120°,船的实际航速为20 m/min.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
