6.4.4余弦定理、正弦定理应用举例分层练习(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 6.4.4余弦定理、正弦定理应用举例分层练习(含解析)--人教A版(2019)高数必修二 |

|
|
| 格式 | docx | ||
| 文件大小 | 460.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
课时作业15 余弦定理、正弦定理应用举例
基础强化
1.在一幢10米高的楼顶测得对面一塔吊顶的仰角为60°,塔基的俯角为45°,那么这座塔吊的高是( )
A.10(1+)米 B.10(1+)米
C.5(+)米 D.2(+)米
2.某人遥控一机器人,让机器人从点A出发向正北方向走了2 km到达点B后,向右转105°,然后朝新方向走了x km后到达点C,结果发现机器人在点A的东北方向,则x为( )
A. B.2
C. D.2
3.
如图,飞机飞行的航线AB和地面目标C在同一铅直平面内,在A处测得目标C的俯角为30°,飞行10千米到达B处,测得目标C的俯角为75°,这时B处与地面目标C的距离为( )
A.5千米 B.5千米
C.4千米 D.4千米
4.已知一个足球场地呈南北走向.在一次进攻时,某运动员从A点处开始带球沿正北方向行进16米到达B处,再转向北偏东60°方向行进了24米到达C处,然后起脚射门,则A,C两点的距离为( )
A.8米 B.8米
C.32米 D.8米
5.
(多选)为了测量B,C之间的距离,在河的南岸A,C处测量(测量工具:量角器、卷尺),如图所示.下面是四位同学所测得的数据记录,你认为不合理的有( )
A.c与α B.c与b
C.b,c与β D.b,α与γ
6.(多选)某人在A处向正东方向走x km后到达B处,他沿南偏西60°方向走3 km到达C处,这时他离出发点 km,那么x的值可以是( )
A. B.2 C. D.2
7.海上有A、B、C三个小岛,其中B岛在A岛的正东方向10海里处,C岛在A岛北偏东30°方向上,且在B岛北偏西60°方向上,则B、C两岛间的距离为________海里.
8.一船自西向东航行,上午10时到达灯塔P的南偏西60°、距塔20海里的M处,上午11时到达这座灯塔的东偏南30°方向的N处,则该船航行的速度为________海里/时.
9.已知飞机从A地按北偏东30°的方向飞行2 000 km到达B地,再从B地按南偏东30°的方向飞行2 000 km到达C地,再从C地按西南方向飞行1 000 km到达D地.求D地与A地之间的距离.
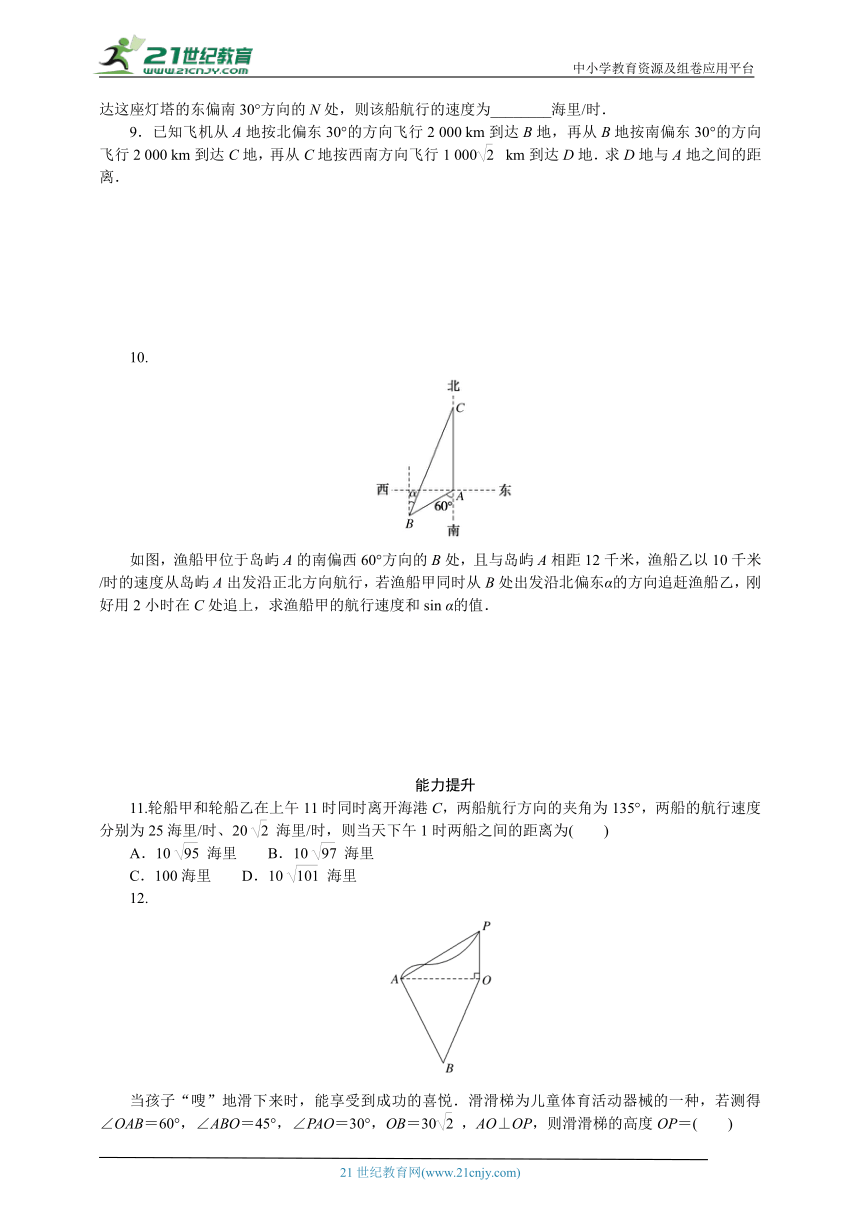
10.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12千米,渔船乙以10千米/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时在C处追上,求渔船甲的航行速度和sin α的值.
能力提升
11.轮船甲和轮船乙在上午11时同时离开海港C,两船航行方向的夹角为135°,两船的航行速度分别为25海里/时、20海里/时,则当天下午1时两船之间的距离为( )
A.10海里 B.10海里
C.100海里 D.10海里
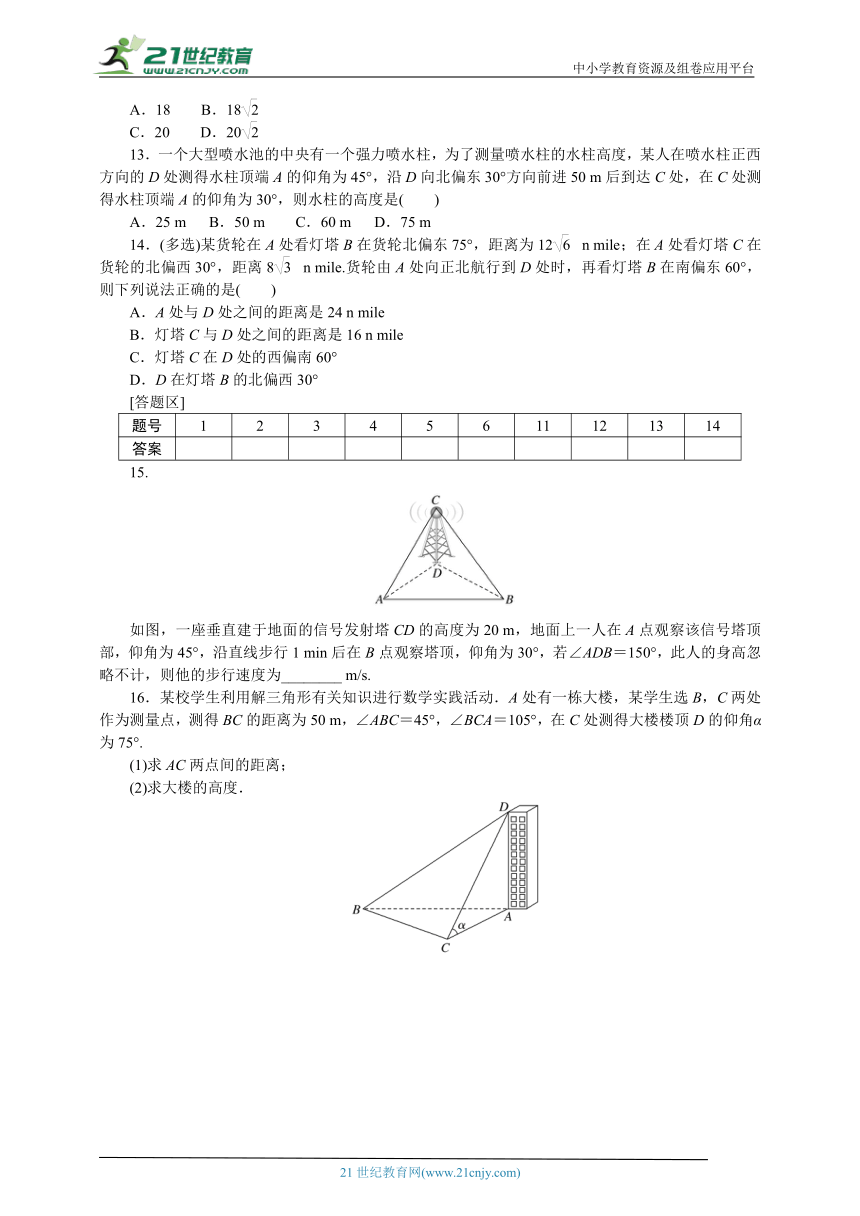
12.
当孩子“嗖”地滑下来时,能享受到成功的喜悦.滑滑梯为儿童体育活动器械的一种,若测得∠OAB=60°,∠ABO=45°,∠PAO=30°,OB=30,AO⊥OP,则滑滑梯的高度OP=( )
A.18 B.18
C.20 D.20
13.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱的水柱高度,某人在喷水柱正西方向的D处测得水柱顶端A的仰角为45°,沿D向北偏东30°方向前进50 m后到达C处,在C处测得水柱顶端A的仰角为30°,则水柱的高度是( )
A.25 m B.50 m C.60 m D.75 m
14.(多选)某货轮在A处看灯塔B在货轮北偏东75°,距离为12 n mile;在A处看灯塔C在货轮的北偏西30°,距离8 n mile.货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°,则下列说法正确的是( )
A.A处与D处之间的距离是24 n mile
B.灯塔C与D处之间的距离是16 n mile
C.灯塔C在D处的西偏南60°
D.D在灯塔B的北偏西30°
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.
如图,一座垂直建于地面的信号发射塔CD的高度为20 m,地面上一人在A点观察该信号塔顶部,仰角为45°,沿直线步行1 min后在B点观察塔顶,仰角为30°,若∠ADB=150°,此人的身高忽略不计,则他的步行速度为________ m/s.
16.某校学生利用解三角形有关知识进行数学实践活动.A处有一栋大楼,某学生选B,C两处作为测量点,测得BC的距离为50 m,∠ABC=45°,∠BCA=105°,在C处测得大楼楼顶D的仰角α为75°.
(1)求AC两点间的距离;
(2)求大楼的高度.
课时作业15 余弦定理、正弦定理应用举例
1.解析:根据题意作图如下:
由题意知AB=10米,仰角∠DAE=60°,俯角∠CAE=45°,在等腰直角三角形CAE中,AE=EC=AB=10米,在直角三角形DAE中,∠DAE=60°,
所以DE=AE tan ∠DAE=AE tan ∠60°=10(米),所以塔高CD=10+10=10(1+)(米).故选B.
答案:B
2.解析:由题意可知∠ACB=60°,∠BAC=45°,由正弦定理可得=,即x=2.故选D.
答案:D
3.解析:根据题意可知AB=10千米,C=75°-30°=45°.在△ABC中,由正弦定理得=,即BC==5(千米).故选B.
答案:B
4.解析:
如图,根据题意可知AB=16米,BC=24米,∠ABC=120°.根据余弦定理可得AC2=AB2+BC2-2AB·BC·cos 120°=162+242-2×16×24×(-),解得AC=8(米).故选D.
答案:D
5.解析:因为A,C在河的同一侧,所以可以测量b,α与γ.故选ABC.
答案:ABC
6.解析:如图,由条件可知,|AB|=x km,∠ABC=30°,|BC|=3 km,|AC|= km,根据余弦定理可知3=x2+9-2·3x·,即x2-3x+6=0,解得x=或2.故选AB.
答案:AB
7.解析:由题设可得如图所示的示意图:
则∠ACB=90°,∠CAB=60°,∠CBA=30°,且AB=10海里.故BC=10×sin ∠CAB=10×=5(海里).
答案:5
8.解析:如图,在△MNP中,由正弦定理可得,
MN==20(海里),则这艘船的航行速度v==20(海里/时).
答案:20
9.解析:由题意得AB=BC=2 000 km,∠ABC=60°,所以AC=2 000 km,因为∠ACD=45°,CD=1 000 km,所以AD==1 000(km),所以AD=CD=1 000 km,∠CAD=45°,D地在A地的南偏东45°,D地距A地1 000 km.
10.解析:由已知得,AB=12千米,AC=20千米,∠BAC=120°,
根据余弦定理可得:
BC2=AB2+AC2-2AB·AC cos ∠BAC=122+202-2×12×20×(-)=784,
则BC=28千米,渔船甲的速度v==14(千米/时)
在△ABC中,∠BCA=α,
由正弦定理得=,∴=,∴sin α=.
11.解析:设轮船甲、乙在下午1时所处的位置分别为A和B,由题可知CA=50海里,CB=40海里,∠ACB=135°,则AB2=CA2+CB2-2CA·CB·cos ∠ACB=502+(40)2-2×50×40×(-)=9 700,故AB=10海里.故选B.
答案:B
12.解析:在△ABO中,由正弦定理得=,即=,解得OA=20,因为AO⊥OP,∠PAO=30°,所以OP=OA·tan 30°=20×=20.故选C.
答案:C
13.解析:如图,
AB为水柱,高度设为h m,D在B的正西方向,C在D的北偏东30°方向.且CD=50 m,∠ACB=30°,∠ADB=45°.在△ABD中,AB=h m,∠ABD=90°,∠ADB=45°,所以BD=h m,在△ABC中,AB=h m,∠ABC=90°,∠ACB=30°,所以BC=h m.在△CDB中,∠CDB=60°,由余弦定理得cos 60°==,∴h=-50(舍)或h=25.故选A.
答案:A
14.解析:
由题意可知∠ADB=60°,∠BAD=75°,∠CAD=30°,所以∠B=180°-60°-75°=45°,AB=12 n mile,AC=8 n mile,在△ABD中,由正弦定理得=,所以AD==24(n mile),故A正确;在△ACD中,由余弦定理得
CD=,
即CD= =8(n mile),故B错误;因为CD=AC,所以∠CDA=∠CAD=30°,所以灯塔C在D处的西偏南60°,故C正确;由∠ADB=60°,D在灯塔B的北偏西60°处,故D错误.故选AC.
答案:AC
15.解析:在Rt△ADC中,∠CAD=45°,CD=20 m,则AD=20 m;在Rt△BDC中,∠CBD=30°,CD=20 m,则BD=20 m;在△ABD中,由余弦定理AB2=AD2+BD2-2AD·BD·cos ∠ADB=202+(20)2-2×20×20×(-)=2 800,可得AB=20(m),所以步行速度为= (m/s).
答案:
16.解析:(1)因为∠BAC=180°-105°-45°=30°,
在△ABC中,由正弦定理得=,
即=,所以AC=50 m,
即AC两点的距离为50 m.
(2)在△DCA中,因为∠DAC=90°,=tan α,
所以AD=AC tan 75°=50tan 75°,
又tan 75°=tan (45°+30°)===2+,
所以AD=50(2+)=(100+50) m,
即大楼的高度为(100+50) m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业15 余弦定理、正弦定理应用举例
基础强化
1.在一幢10米高的楼顶测得对面一塔吊顶的仰角为60°,塔基的俯角为45°,那么这座塔吊的高是( )
A.10(1+)米 B.10(1+)米
C.5(+)米 D.2(+)米
2.某人遥控一机器人,让机器人从点A出发向正北方向走了2 km到达点B后,向右转105°,然后朝新方向走了x km后到达点C,结果发现机器人在点A的东北方向,则x为( )
A. B.2
C. D.2
3.
如图,飞机飞行的航线AB和地面目标C在同一铅直平面内,在A处测得目标C的俯角为30°,飞行10千米到达B处,测得目标C的俯角为75°,这时B处与地面目标C的距离为( )
A.5千米 B.5千米
C.4千米 D.4千米
4.已知一个足球场地呈南北走向.在一次进攻时,某运动员从A点处开始带球沿正北方向行进16米到达B处,再转向北偏东60°方向行进了24米到达C处,然后起脚射门,则A,C两点的距离为( )
A.8米 B.8米
C.32米 D.8米
5.
(多选)为了测量B,C之间的距离,在河的南岸A,C处测量(测量工具:量角器、卷尺),如图所示.下面是四位同学所测得的数据记录,你认为不合理的有( )
A.c与α B.c与b
C.b,c与β D.b,α与γ
6.(多选)某人在A处向正东方向走x km后到达B处,他沿南偏西60°方向走3 km到达C处,这时他离出发点 km,那么x的值可以是( )
A. B.2 C. D.2
7.海上有A、B、C三个小岛,其中B岛在A岛的正东方向10海里处,C岛在A岛北偏东30°方向上,且在B岛北偏西60°方向上,则B、C两岛间的距离为________海里.
8.一船自西向东航行,上午10时到达灯塔P的南偏西60°、距塔20海里的M处,上午11时到达这座灯塔的东偏南30°方向的N处,则该船航行的速度为________海里/时.
9.已知飞机从A地按北偏东30°的方向飞行2 000 km到达B地,再从B地按南偏东30°的方向飞行2 000 km到达C地,再从C地按西南方向飞行1 000 km到达D地.求D地与A地之间的距离.
10.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12千米,渔船乙以10千米/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时在C处追上,求渔船甲的航行速度和sin α的值.
能力提升
11.轮船甲和轮船乙在上午11时同时离开海港C,两船航行方向的夹角为135°,两船的航行速度分别为25海里/时、20海里/时,则当天下午1时两船之间的距离为( )
A.10海里 B.10海里
C.100海里 D.10海里
12.
当孩子“嗖”地滑下来时,能享受到成功的喜悦.滑滑梯为儿童体育活动器械的一种,若测得∠OAB=60°,∠ABO=45°,∠PAO=30°,OB=30,AO⊥OP,则滑滑梯的高度OP=( )
A.18 B.18
C.20 D.20
13.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱的水柱高度,某人在喷水柱正西方向的D处测得水柱顶端A的仰角为45°,沿D向北偏东30°方向前进50 m后到达C处,在C处测得水柱顶端A的仰角为30°,则水柱的高度是( )
A.25 m B.50 m C.60 m D.75 m
14.(多选)某货轮在A处看灯塔B在货轮北偏东75°,距离为12 n mile;在A处看灯塔C在货轮的北偏西30°,距离8 n mile.货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°,则下列说法正确的是( )
A.A处与D处之间的距离是24 n mile
B.灯塔C与D处之间的距离是16 n mile
C.灯塔C在D处的西偏南60°
D.D在灯塔B的北偏西30°
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.
如图,一座垂直建于地面的信号发射塔CD的高度为20 m,地面上一人在A点观察该信号塔顶部,仰角为45°,沿直线步行1 min后在B点观察塔顶,仰角为30°,若∠ADB=150°,此人的身高忽略不计,则他的步行速度为________ m/s.
16.某校学生利用解三角形有关知识进行数学实践活动.A处有一栋大楼,某学生选B,C两处作为测量点,测得BC的距离为50 m,∠ABC=45°,∠BCA=105°,在C处测得大楼楼顶D的仰角α为75°.
(1)求AC两点间的距离;
(2)求大楼的高度.
课时作业15 余弦定理、正弦定理应用举例
1.解析:根据题意作图如下:
由题意知AB=10米,仰角∠DAE=60°,俯角∠CAE=45°,在等腰直角三角形CAE中,AE=EC=AB=10米,在直角三角形DAE中,∠DAE=60°,
所以DE=AE tan ∠DAE=AE tan ∠60°=10(米),所以塔高CD=10+10=10(1+)(米).故选B.
答案:B
2.解析:由题意可知∠ACB=60°,∠BAC=45°,由正弦定理可得=,即x=2.故选D.
答案:D
3.解析:根据题意可知AB=10千米,C=75°-30°=45°.在△ABC中,由正弦定理得=,即BC==5(千米).故选B.
答案:B
4.解析:
如图,根据题意可知AB=16米,BC=24米,∠ABC=120°.根据余弦定理可得AC2=AB2+BC2-2AB·BC·cos 120°=162+242-2×16×24×(-),解得AC=8(米).故选D.
答案:D
5.解析:因为A,C在河的同一侧,所以可以测量b,α与γ.故选ABC.
答案:ABC
6.解析:如图,由条件可知,|AB|=x km,∠ABC=30°,|BC|=3 km,|AC|= km,根据余弦定理可知3=x2+9-2·3x·,即x2-3x+6=0,解得x=或2.故选AB.
答案:AB
7.解析:由题设可得如图所示的示意图:
则∠ACB=90°,∠CAB=60°,∠CBA=30°,且AB=10海里.故BC=10×sin ∠CAB=10×=5(海里).
答案:5
8.解析:如图,在△MNP中,由正弦定理可得,
MN==20(海里),则这艘船的航行速度v==20(海里/时).
答案:20
9.解析:由题意得AB=BC=2 000 km,∠ABC=60°,所以AC=2 000 km,因为∠ACD=45°,CD=1 000 km,所以AD==1 000(km),所以AD=CD=1 000 km,∠CAD=45°,D地在A地的南偏东45°,D地距A地1 000 km.
10.解析:由已知得,AB=12千米,AC=20千米,∠BAC=120°,
根据余弦定理可得:
BC2=AB2+AC2-2AB·AC cos ∠BAC=122+202-2×12×20×(-)=784,
则BC=28千米,渔船甲的速度v==14(千米/时)
在△ABC中,∠BCA=α,
由正弦定理得=,∴=,∴sin α=.
11.解析:设轮船甲、乙在下午1时所处的位置分别为A和B,由题可知CA=50海里,CB=40海里,∠ACB=135°,则AB2=CA2+CB2-2CA·CB·cos ∠ACB=502+(40)2-2×50×40×(-)=9 700,故AB=10海里.故选B.
答案:B
12.解析:在△ABO中,由正弦定理得=,即=,解得OA=20,因为AO⊥OP,∠PAO=30°,所以OP=OA·tan 30°=20×=20.故选C.
答案:C
13.解析:如图,
AB为水柱,高度设为h m,D在B的正西方向,C在D的北偏东30°方向.且CD=50 m,∠ACB=30°,∠ADB=45°.在△ABD中,AB=h m,∠ABD=90°,∠ADB=45°,所以BD=h m,在△ABC中,AB=h m,∠ABC=90°,∠ACB=30°,所以BC=h m.在△CDB中,∠CDB=60°,由余弦定理得cos 60°==,∴h=-50(舍)或h=25.故选A.
答案:A
14.解析:
由题意可知∠ADB=60°,∠BAD=75°,∠CAD=30°,所以∠B=180°-60°-75°=45°,AB=12 n mile,AC=8 n mile,在△ABD中,由正弦定理得=,所以AD==24(n mile),故A正确;在△ACD中,由余弦定理得
CD=,
即CD= =8(n mile),故B错误;因为CD=AC,所以∠CDA=∠CAD=30°,所以灯塔C在D处的西偏南60°,故C正确;由∠ADB=60°,D在灯塔B的北偏西60°处,故D错误.故选AC.
答案:AC
15.解析:在Rt△ADC中,∠CAD=45°,CD=20 m,则AD=20 m;在Rt△BDC中,∠CBD=30°,CD=20 m,则BD=20 m;在△ABD中,由余弦定理AB2=AD2+BD2-2AD·BD·cos ∠ADB=202+(20)2-2×20×20×(-)=2 800,可得AB=20(m),所以步行速度为= (m/s).
答案:
16.解析:(1)因为∠BAC=180°-105°-45°=30°,
在△ABC中,由正弦定理得=,
即=,所以AC=50 m,
即AC两点的距离为50 m.
(2)在△DCA中,因为∠DAC=90°,=tan α,
所以AD=AC tan 75°=50tan 75°,
又tan 75°=tan (45°+30°)===2+,
所以AD=50(2+)=(100+50) m,
即大楼的高度为(100+50) m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
