8.1.1棱柱、棱锥、棱台分层练习(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 8.1.1棱柱、棱锥、棱台分层练习(含解析)--人教A版(2019)高数必修二 |

|
|
| 格式 | docx | ||
| 文件大小 | 525.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
课时作业21 棱柱、棱锥、棱台
基础强化
1.如图所示,观察四个几何体,其中判断正确的是( )
A.是棱台
B.是圆台
C.不是棱柱
D.是棱锥
2.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥共有六个顶点
D.任何棱锥都只有一个底面
3.下面没有体对角线的一种几何体是( )
A.三棱柱 B.四棱柱
C.五棱柱 D.六棱柱
4.一个几何体由六个面组成,其中两个面是互相平行且相似的四边形,其余各面都是全等的等腰梯形,则这个几何体是( )
A.三棱柱 B.三棱台
C.四棱柱 D.四棱台
5.(多选)某几何体有6个顶点,则该几何体可能是( )
A.五棱锥 B.三棱柱
C.三棱台 D.四棱台
6.(多选)下面说法正确的是( )
A.多面体至少有四个面
B.平行六面体六个面都是平行四边形
C.棱台的侧面都是梯形
D.长方体、正方体都是正四棱柱
7.已知某多面体的平面展开图如图所示,其中是三棱柱的有________个.
8.一长方体共一顶点的三条棱长分别为2、3、4,则这个长方体的对角线长________.
9.如图所示的平面图形沿虚线折叠,能折叠成什么样的立体图形?
10.试从正方体ABCD A1B1C1D1的八个顶点中任取若干个点,连接后构成以下空间几何体,画图并用适当的符号表示出来.
(1)只有一个面是等边三角形的三棱锥;
(2)四个面都是等边三角形的三棱锥.
能力提升
11.下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
12.一个棱锥的各棱长都相等,那么这个棱锥一定不是( )
A.三棱锥 B.四棱锥
C.五棱锥 D.六棱锥
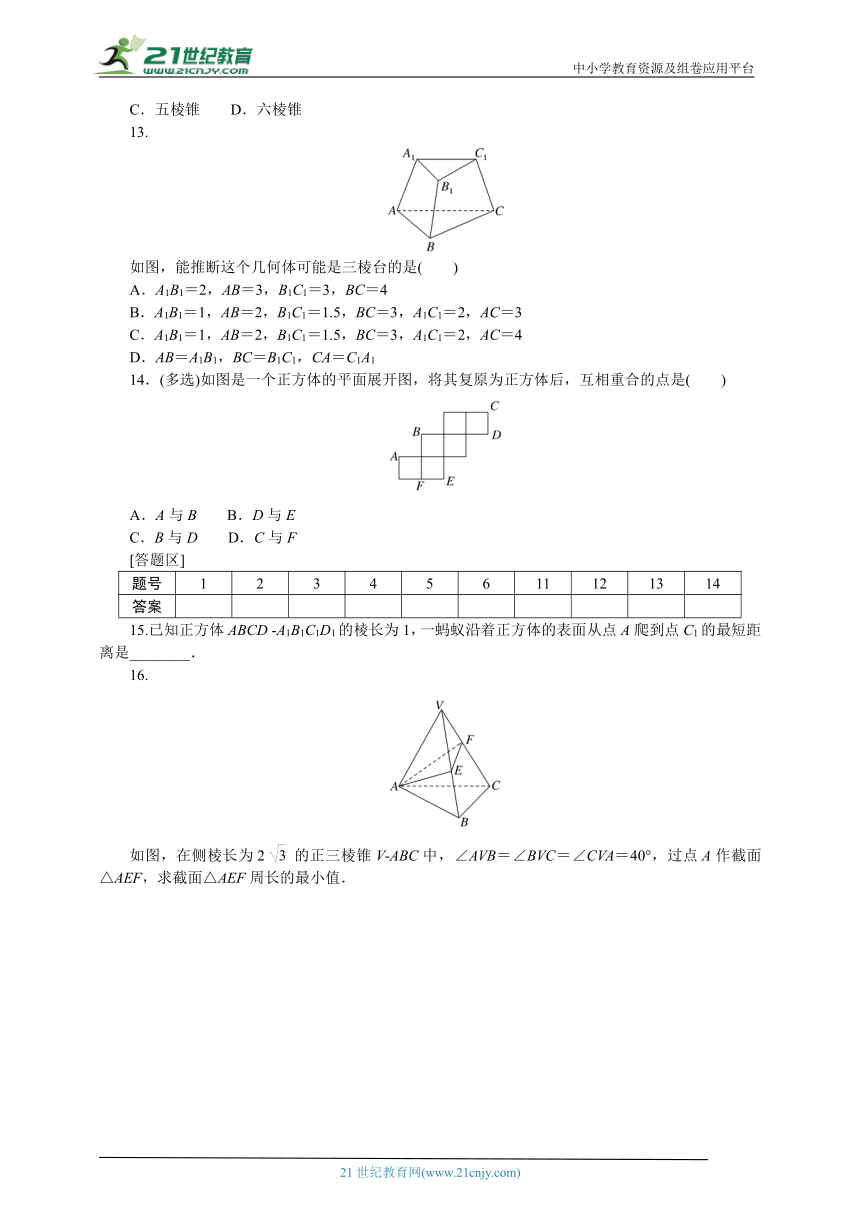
13.
如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=3
C.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
14.(多选)如图是一个正方体的平面展开图,将其复原为正方体后,互相重合的点是( )
A.A与B B.D与E
C.B与D D.C与F
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知正方体ABCD A1B1C1D1的棱长为1,一蚂蚁沿着正方体的表面从点A爬到点C1的最短距离是________.
16.
如图,在侧棱长为2的正三棱锥V ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面△AEF,求截面△AEF周长的最小值.
课时作业21 棱柱、棱锥、棱台
1.解析:对于A,侧棱延长线不交于一点,不符合棱台的定义,所以A错误;对于B,上下两个面不平行,不符合圆台的定义,所以B错误;对于C,将几何体竖直起来看,符合棱柱的定义,所以C错误;对于D,符合棱锥的定义,正确.故选D.
答案:D
2.解析:对于A,四棱锥共有八条棱,故A错误;对于B,五棱锥共有六个面,故B错误;对于C,六棱锥共有一个顶点,故C错误;对于D,根据棱锥的定义知,D正确.故选D.
答案:D
3.解析:三棱柱只有面对角线,没有体对角线.故选A.
答案:A
4.解析:不妨假定两个平行的面是上下底面,并且必须是6个面,显然三棱柱和三棱台不满足要求,四棱柱要求各侧面均为平行四边形,上下两个平面为全等的四边形,不满足要求,四棱台上下两个底面相互平行,其余各面都是梯形,故满足条件的几何体是四棱台.故选D.
答案:D
5.解析:四棱台有8个顶点,五棱锥有1个顶点,不符合题意,其他都是6个顶点.故选BC.
答案:BC
6.解析:对于A,最简单的多面体是三棱锥,有4个面,所以多面体的面数大于等于4,所以“多面体至少有四个面”正确,故A正确;对于B,由平行六面体的定义可知平行六面体六个面都是平行四边形,故B正确;对于C,由棱台的定义可知棱台的侧面都是梯形,故C正确;对于D,按照正四棱柱的定义,底面必须是正方形,所以底面不是正方形的长方体就不是正四棱柱,故D错误.故选ABC.
答案:ABC
7.解析:根据平面展开图,还原几何体如图所示:
故第二个和第四个为三棱柱,三棱柱的个数有2个.
答案:2
8.解析:长方体的对角线l===.
答案:
9.解析:(1)中一个面是正五边形,其余各面都是等腰三角形,故(1)能折成正五棱锥.
(2)中有三个面是梯形,有两个面是相似的三角形,故(2)能折成三棱台.
10.解析:(1)如图所示,三棱锥A1 AB1D1(或三棱锥A A1BD,三棱锥B AB1C,三棱锥C BDC1,三棱锥D ACD1,三棱锥B1 A1BC1,三棱锥C1 B1CD1,三棱锥D1 A1C1D答案不唯一).
(2)如图所示,三棱锥B1 ACD1(或三棱锥A1-BDC1,答案不唯一).
11.解析:对于A,长方体是四棱柱,底面不是长方形的直四棱柱不是长方体,错误;对于B,棱台的侧棱延长线必须相交于一点,错误;对于C,各侧面都是正方形,底面不是正方形(如菱形)的四棱柱不是正方体,错误;对于D,棱柱的侧棱相等,侧面都是平行四边形,正确.故选D.
答案:D
12.解析:正六棱锥的底面是个正六边形,正六边形共由6个等边三角形构成,设每个等边三角形的边长为r,正六棱锥的高为h,正六棱锥的侧棱长为l,由正六棱锥的高h、底面的半径r、侧棱长l构成直角三角形得,h2+r2=l2,故侧棱长l和底面正六边形的边长r不可能相等.故选D.
答案:D
13.解析:A选项,≠,所以几何体不是三棱台,A选项错误.B选项,≠,所以几何体不是三棱台,B选项错误.C选项,==,所以几何体是三棱台,C选项正确.D选项,该几何体可能是三棱柱,D选项错误.故选C.
答案:C
14.解析:将平面展开图,还原正方体如图所示:
所以互相重合的点是A与B,D与E,C与F.故选ABD.
答案:ABD
15.解析:如图所示,将正方体ABCD A1B1C1D1的侧面ABB1A1与BB1C1C展开,则最短距离为AC1===.
答案:
16.解析:沿着侧棱VA把正三棱锥V ABC展开在一个平面内,如图.
则AA1的长即为截面△AEF周长的最小值,且∠AVA1=∠AVB+∠BVC+∠CVA=120°.
取AA1的中点为D,连接VD,则VD⊥AA1,且VA=2,∠AVD=60°,
在△VAA1中,AD=VA1sin 60°=3,所以AA1=2AD=6,
故截面△AEF周长的最小值为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业21 棱柱、棱锥、棱台
基础强化
1.如图所示,观察四个几何体,其中判断正确的是( )
A.是棱台
B.是圆台
C.不是棱柱
D.是棱锥
2.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥共有六个顶点
D.任何棱锥都只有一个底面
3.下面没有体对角线的一种几何体是( )
A.三棱柱 B.四棱柱
C.五棱柱 D.六棱柱
4.一个几何体由六个面组成,其中两个面是互相平行且相似的四边形,其余各面都是全等的等腰梯形,则这个几何体是( )
A.三棱柱 B.三棱台
C.四棱柱 D.四棱台
5.(多选)某几何体有6个顶点,则该几何体可能是( )
A.五棱锥 B.三棱柱
C.三棱台 D.四棱台
6.(多选)下面说法正确的是( )
A.多面体至少有四个面
B.平行六面体六个面都是平行四边形
C.棱台的侧面都是梯形
D.长方体、正方体都是正四棱柱
7.已知某多面体的平面展开图如图所示,其中是三棱柱的有________个.
8.一长方体共一顶点的三条棱长分别为2、3、4,则这个长方体的对角线长________.
9.如图所示的平面图形沿虚线折叠,能折叠成什么样的立体图形?
10.试从正方体ABCD A1B1C1D1的八个顶点中任取若干个点,连接后构成以下空间几何体,画图并用适当的符号表示出来.
(1)只有一个面是等边三角形的三棱锥;
(2)四个面都是等边三角形的三棱锥.
能力提升
11.下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
12.一个棱锥的各棱长都相等,那么这个棱锥一定不是( )
A.三棱锥 B.四棱锥
C.五棱锥 D.六棱锥
13.
如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=3
C.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
14.(多选)如图是一个正方体的平面展开图,将其复原为正方体后,互相重合的点是( )
A.A与B B.D与E
C.B与D D.C与F
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知正方体ABCD A1B1C1D1的棱长为1,一蚂蚁沿着正方体的表面从点A爬到点C1的最短距离是________.
16.
如图,在侧棱长为2的正三棱锥V ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面△AEF,求截面△AEF周长的最小值.
课时作业21 棱柱、棱锥、棱台
1.解析:对于A,侧棱延长线不交于一点,不符合棱台的定义,所以A错误;对于B,上下两个面不平行,不符合圆台的定义,所以B错误;对于C,将几何体竖直起来看,符合棱柱的定义,所以C错误;对于D,符合棱锥的定义,正确.故选D.
答案:D
2.解析:对于A,四棱锥共有八条棱,故A错误;对于B,五棱锥共有六个面,故B错误;对于C,六棱锥共有一个顶点,故C错误;对于D,根据棱锥的定义知,D正确.故选D.
答案:D
3.解析:三棱柱只有面对角线,没有体对角线.故选A.
答案:A
4.解析:不妨假定两个平行的面是上下底面,并且必须是6个面,显然三棱柱和三棱台不满足要求,四棱柱要求各侧面均为平行四边形,上下两个平面为全等的四边形,不满足要求,四棱台上下两个底面相互平行,其余各面都是梯形,故满足条件的几何体是四棱台.故选D.
答案:D
5.解析:四棱台有8个顶点,五棱锥有1个顶点,不符合题意,其他都是6个顶点.故选BC.
答案:BC
6.解析:对于A,最简单的多面体是三棱锥,有4个面,所以多面体的面数大于等于4,所以“多面体至少有四个面”正确,故A正确;对于B,由平行六面体的定义可知平行六面体六个面都是平行四边形,故B正确;对于C,由棱台的定义可知棱台的侧面都是梯形,故C正确;对于D,按照正四棱柱的定义,底面必须是正方形,所以底面不是正方形的长方体就不是正四棱柱,故D错误.故选ABC.
答案:ABC
7.解析:根据平面展开图,还原几何体如图所示:
故第二个和第四个为三棱柱,三棱柱的个数有2个.
答案:2
8.解析:长方体的对角线l===.
答案:
9.解析:(1)中一个面是正五边形,其余各面都是等腰三角形,故(1)能折成正五棱锥.
(2)中有三个面是梯形,有两个面是相似的三角形,故(2)能折成三棱台.
10.解析:(1)如图所示,三棱锥A1 AB1D1(或三棱锥A A1BD,三棱锥B AB1C,三棱锥C BDC1,三棱锥D ACD1,三棱锥B1 A1BC1,三棱锥C1 B1CD1,三棱锥D1 A1C1D答案不唯一).
(2)如图所示,三棱锥B1 ACD1(或三棱锥A1-BDC1,答案不唯一).
11.解析:对于A,长方体是四棱柱,底面不是长方形的直四棱柱不是长方体,错误;对于B,棱台的侧棱延长线必须相交于一点,错误;对于C,各侧面都是正方形,底面不是正方形(如菱形)的四棱柱不是正方体,错误;对于D,棱柱的侧棱相等,侧面都是平行四边形,正确.故选D.
答案:D
12.解析:正六棱锥的底面是个正六边形,正六边形共由6个等边三角形构成,设每个等边三角形的边长为r,正六棱锥的高为h,正六棱锥的侧棱长为l,由正六棱锥的高h、底面的半径r、侧棱长l构成直角三角形得,h2+r2=l2,故侧棱长l和底面正六边形的边长r不可能相等.故选D.
答案:D
13.解析:A选项,≠,所以几何体不是三棱台,A选项错误.B选项,≠,所以几何体不是三棱台,B选项错误.C选项,==,所以几何体是三棱台,C选项正确.D选项,该几何体可能是三棱柱,D选项错误.故选C.
答案:C
14.解析:将平面展开图,还原正方体如图所示:
所以互相重合的点是A与B,D与E,C与F.故选ABD.
答案:ABD
15.解析:如图所示,将正方体ABCD A1B1C1D1的侧面ABB1A1与BB1C1C展开,则最短距离为AC1===.
答案:
16.解析:沿着侧棱VA把正三棱锥V ABC展开在一个平面内,如图.
则AA1的长即为截面△AEF周长的最小值,且∠AVA1=∠AVB+∠BVC+∠CVA=120°.
取AA1的中点为D,连接VD,则VD⊥AA1,且VA=2,∠AVD=60°,
在△VAA1中,AD=VA1sin 60°=3,所以AA1=2AD=6,
故截面△AEF周长的最小值为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
