8.3.1棱柱、棱锥、棱台的表面积和体积分层练习(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 8.3.1棱柱、棱锥、棱台的表面积和体积分层练习(含解析)--人教A版(2019)高数必修二 |  | |
| 格式 | docx | ||
| 文件大小 | 500.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 14:26:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
课时作业24 棱柱、棱锥、棱台的表面积和体积
基础强化
1.一个长方体的三个面的面积分别为,,,则这个长方体的体积为( )
A.6 B.
C.3 D.2
2.如果正方体ABCD A′B′C′D′的棱长为a,那么四面体A′ ABD的体积是( )
A. B.
C. D.
3.若正四棱台的上、下底面边长分别为1,2,高为2,则该正四棱台的体积为( )
A. B.
C. D.14
4.设正四棱柱的一条对角线长为3,它的底面积是4,则它的体积是( )
A.4 B.8 C. D.4或
5.如图是一个下半部分为正方体、上半部分为正三棱柱的盒子(中间连通).若其表面积为(448+32)cm2,则其体积为( )
A.(512+128)cm3 B.(216+128)cm3
C.(512+64)cm3 D.(216+64)cm3
6.(多选)正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥的侧面积为
7.已知长方体全部棱长的和为36,表面积为52,则其对角线的长为________.
8.设正六棱柱的底面边长为1,侧棱长为5,那么它的体积为________.
9.已知某个三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,求它的表面积.
10.
已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
能力提升
11.边长为3的正方体切成27个全等的小正方体,则表面积之和比原来增加了( )
A.36 B.72
C.108 D.240
12.如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N,顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6
C.7 D.8
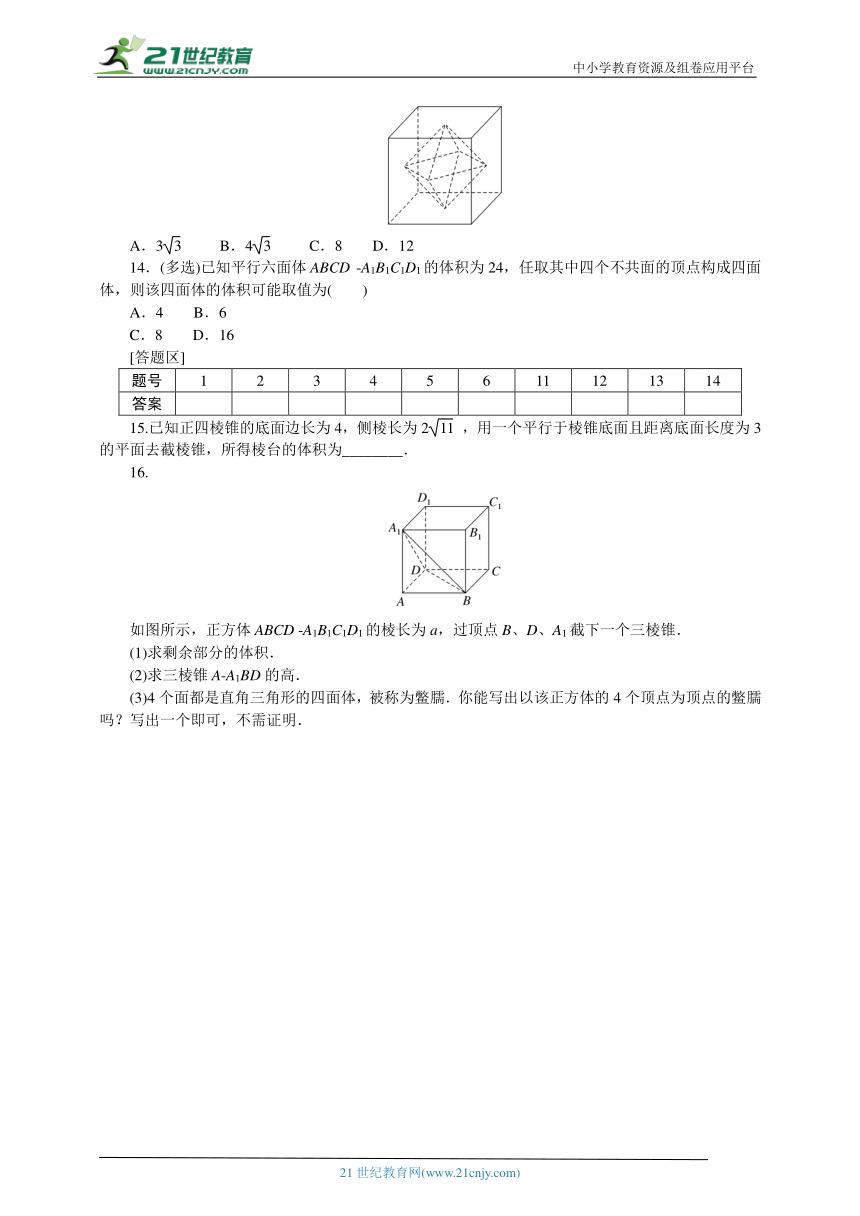
13.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的表面积为( )
A.3 B.4 C.8 D.12
14.(多选)已知平行六面体ABCD A1B1C1D1的体积为24,任取其中四个不共面的顶点构成四面体,则该四面体的体积可能取值为( )
A.4 B.6
C.8 D.16
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知正四棱锥的底面边长为4,侧棱长为2,用一个平行于棱锥底面且距离底面长度为3的平面去截棱锥,所得棱台的体积为________.
16.
如图所示,正方体ABCD A1B1C1D1的棱长为a,过顶点B、D、A1截下一个三棱锥.
(1)求剩余部分的体积.
(2)求三棱锥A A1BD的高.
(3)4个面都是直角三角形的四面体,被称为鳖臑.你能写出以该正方体的4个顶点为顶点的鳖臑吗?写出一个即可,不需证明.
课时作业24 棱柱、棱锥、棱台的表面积和体积
1.解析:设长方体的长、宽、高分别为x、y、z,则xy=,yz=,xz=,∴(xyz)2=6,∴V=xyz=.故选B.
答案:B
2.解析:VA′ ABD=·S△ABD·AA′=××a×a×a=.故选D.
答案:D
3.解析:V台=(S+S′+)h=(1+4+)×2=.故选C.
答案:C
4.解析:设正四棱柱的底面边长为a,高为h,则a2=4且2a2+h2=9,解得a=2,h=1,所以正四棱柱的体积为V=a2h=4.故选A.
答案:A
5.解析:设正方体的棱长为a cm,则5a2+2a2+a2×2=448+32,解得a=8.该几何体的体积为a3+a2·a=512+128(cm3).故选A.
答案:A
6.解析:
设E为等边三角形ADC的中心,F为CD的中点,连接PF,EF,PE,则PE为正三棱锥的高,PF为斜高,又PF= =,EF=×=,故PE= =3,故AB正确.而正三棱锥的体积为×3××9=,侧面积为3××3×=,故C错误,D正确.故选ABD.
答案:ABD
7.解析:设长,宽,高分别为x,y,z,则2(xy+xz+yz)=52,4(x+y+z)=36,可得体对角线的长为===.
答案:
8.解析:由正六棱柱可得底面为正六边形,则底面积S=×12×sin 60°×6=,即正六棱柱的体积V=Sh=×5=.
答案:
9.解析:由题意可知该三棱柱为正三棱柱,
∵正三棱柱的侧面展开图是边长分别为6和4的矩形,
∴有如下两种情况:
①6是底面周长,4是三棱柱的高,
此时正三角形边长为2,
此底面积S1=×2×2sin 60°=×2×2×=,
表面积S2=24+2;
②4是底面周长,6是三棱柱的高,
此时正三角形边长为,
此时底面积S3=×sin 60°=,
表面积S4=24+.
所以该三棱柱的表面积是24+2或24+.
10.解析:(1)几何体的体积为
V=·S矩形·h=×6×8×4=64.
(2)正侧面及相对侧面底边上的高为
h1==5.
左、右侧面的底边上的高为
h2==4.
故几何体的侧面面积为
S=2×(×8×5+×6×4)=40+24.
11.解析:由已知,边长为3的正方体分成27个全等的小正方体,则小正方体的边长为1,边长为3的正方体表面积为6×3×3=54,每个小正方体的表面积为6×1×1=6,27个小正方体的表面积之和为6×27=162,162-54=108,所以表面积之和比原来增加了108,故选C.
答案:C
12.解析:如图将正方体还原可得如下图形:
则=××1×1×2=,VD ND1C1=××1×2×2=,=23=8,所以该几何体的体积V=8--=7.故选C.
答案:C
13.解析:由题意知,该几何体是一个由8个全等的正三角形围成的多面体,正三角形的边长为 =,正三角形边上的一条高为 =,所以一个正三角形的面积为××=,所以多面体的表面积为8×=4.故选B.
答案:B
14.解析:设平行六面体的体积为V=24,如左图,当取顶点A1,A,B,D时,则该四面体体积V1=V=×24=4;如右图,当取顶点A,B1,C,D1时,则该四面体体积V2=V-4V1=24-4×4=8.故选AC.
答案:AC
15.解析:
如图,由题意可得EF=3,AF=2,OF==6.因为△OA1E∽△OAF,所以=,解得A1E=,则A1B1=2,=4,S正方形ABCD=16,所以V棱台=(S正方形ABCD++)·EF=28.
答案:28
16.解析:(1)设正方体的棱长为a,
则V=a3-××a=a3.
(2)==××a=a3,
易知△A1BD为等边三角形,且边长为a,其面积为S=×a×a×sin 60°=a2,
∴a3=×a2h,解得h=a.
即三棱锥A A1BD的高为a.
(3)由鳖臑定义可知,三棱锥D1 DBC是一个鳖臑.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业24 棱柱、棱锥、棱台的表面积和体积
基础强化
1.一个长方体的三个面的面积分别为,,,则这个长方体的体积为( )
A.6 B.
C.3 D.2
2.如果正方体ABCD A′B′C′D′的棱长为a,那么四面体A′ ABD的体积是( )
A. B.
C. D.
3.若正四棱台的上、下底面边长分别为1,2,高为2,则该正四棱台的体积为( )
A. B.
C. D.14
4.设正四棱柱的一条对角线长为3,它的底面积是4,则它的体积是( )
A.4 B.8 C. D.4或
5.如图是一个下半部分为正方体、上半部分为正三棱柱的盒子(中间连通).若其表面积为(448+32)cm2,则其体积为( )
A.(512+128)cm3 B.(216+128)cm3
C.(512+64)cm3 D.(216+64)cm3
6.(多选)正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥的侧面积为
7.已知长方体全部棱长的和为36,表面积为52,则其对角线的长为________.
8.设正六棱柱的底面边长为1,侧棱长为5,那么它的体积为________.
9.已知某个三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,求它的表面积.
10.
已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
能力提升
11.边长为3的正方体切成27个全等的小正方体,则表面积之和比原来增加了( )
A.36 B.72
C.108 D.240
12.如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N,顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6
C.7 D.8
13.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的表面积为( )
A.3 B.4 C.8 D.12
14.(多选)已知平行六面体ABCD A1B1C1D1的体积为24,任取其中四个不共面的顶点构成四面体,则该四面体的体积可能取值为( )
A.4 B.6
C.8 D.16
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知正四棱锥的底面边长为4,侧棱长为2,用一个平行于棱锥底面且距离底面长度为3的平面去截棱锥,所得棱台的体积为________.
16.
如图所示,正方体ABCD A1B1C1D1的棱长为a,过顶点B、D、A1截下一个三棱锥.
(1)求剩余部分的体积.
(2)求三棱锥A A1BD的高.
(3)4个面都是直角三角形的四面体,被称为鳖臑.你能写出以该正方体的4个顶点为顶点的鳖臑吗?写出一个即可,不需证明.
课时作业24 棱柱、棱锥、棱台的表面积和体积
1.解析:设长方体的长、宽、高分别为x、y、z,则xy=,yz=,xz=,∴(xyz)2=6,∴V=xyz=.故选B.
答案:B
2.解析:VA′ ABD=·S△ABD·AA′=××a×a×a=.故选D.
答案:D
3.解析:V台=(S+S′+)h=(1+4+)×2=.故选C.
答案:C
4.解析:设正四棱柱的底面边长为a,高为h,则a2=4且2a2+h2=9,解得a=2,h=1,所以正四棱柱的体积为V=a2h=4.故选A.
答案:A
5.解析:设正方体的棱长为a cm,则5a2+2a2+a2×2=448+32,解得a=8.该几何体的体积为a3+a2·a=512+128(cm3).故选A.
答案:A
6.解析:
设E为等边三角形ADC的中心,F为CD的中点,连接PF,EF,PE,则PE为正三棱锥的高,PF为斜高,又PF= =,EF=×=,故PE= =3,故AB正确.而正三棱锥的体积为×3××9=,侧面积为3××3×=,故C错误,D正确.故选ABD.
答案:ABD
7.解析:设长,宽,高分别为x,y,z,则2(xy+xz+yz)=52,4(x+y+z)=36,可得体对角线的长为===.
答案:
8.解析:由正六棱柱可得底面为正六边形,则底面积S=×12×sin 60°×6=,即正六棱柱的体积V=Sh=×5=.
答案:
9.解析:由题意可知该三棱柱为正三棱柱,
∵正三棱柱的侧面展开图是边长分别为6和4的矩形,
∴有如下两种情况:
①6是底面周长,4是三棱柱的高,
此时正三角形边长为2,
此底面积S1=×2×2sin 60°=×2×2×=,
表面积S2=24+2;
②4是底面周长,6是三棱柱的高,
此时正三角形边长为,
此时底面积S3=×sin 60°=,
表面积S4=24+.
所以该三棱柱的表面积是24+2或24+.
10.解析:(1)几何体的体积为
V=·S矩形·h=×6×8×4=64.
(2)正侧面及相对侧面底边上的高为
h1==5.
左、右侧面的底边上的高为
h2==4.
故几何体的侧面面积为
S=2×(×8×5+×6×4)=40+24.
11.解析:由已知,边长为3的正方体分成27个全等的小正方体,则小正方体的边长为1,边长为3的正方体表面积为6×3×3=54,每个小正方体的表面积为6×1×1=6,27个小正方体的表面积之和为6×27=162,162-54=108,所以表面积之和比原来增加了108,故选C.
答案:C
12.解析:如图将正方体还原可得如下图形:
则=××1×1×2=,VD ND1C1=××1×2×2=,=23=8,所以该几何体的体积V=8--=7.故选C.
答案:C
13.解析:由题意知,该几何体是一个由8个全等的正三角形围成的多面体,正三角形的边长为 =,正三角形边上的一条高为 =,所以一个正三角形的面积为××=,所以多面体的表面积为8×=4.故选B.
答案:B
14.解析:设平行六面体的体积为V=24,如左图,当取顶点A1,A,B,D时,则该四面体体积V1=V=×24=4;如右图,当取顶点A,B1,C,D1时,则该四面体体积V2=V-4V1=24-4×4=8.故选AC.
答案:AC
15.解析:
如图,由题意可得EF=3,AF=2,OF==6.因为△OA1E∽△OAF,所以=,解得A1E=,则A1B1=2,=4,S正方形ABCD=16,所以V棱台=(S正方形ABCD++)·EF=28.
答案:28
16.解析:(1)设正方体的棱长为a,
则V=a3-××a=a3.
(2)==××a=a3,
易知△A1BD为等边三角形,且边长为a,其面积为S=×a×a×sin 60°=a2,
∴a3=×a2h,解得h=a.
即三棱锥A A1BD的高为a.
(3)由鳖臑定义可知,三棱锥D1 DBC是一个鳖臑.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
