2023-2024学年数学七年级一元一次不等式和一元一次不等式组单元测试试题(京改版)基础卷一含解析
文档属性
| 名称 | 2023-2024学年数学七年级一元一次不等式和一元一次不等式组单元测试试题(京改版)基础卷一含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 797.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级一元一次不等式和一元一次不等式组(京改版)单元测试 基础卷一 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)已知为实数且,则下列各式一定成立的是( )
A. B. C. D.
2.(本题3分)在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
3.(本题3分)不等式的解集是( )
A. B. C. D.
4.(本题3分)亚运会期间,某商店购进了一批服装,每件进价为元,并以每件元的价格出售,亚运会结束后,商店准备将这批服装降价处理,打折出售,使得每件衣服的利润不低于,根据题意可列出来的不等式为( )
A. B.
C. D.
5.(本题3分)不等式的解集表示在数轴上,你认为正确的是( )
A. B.
C.
D.
6.(本题3分)已知,下列不等式变形中正确的是( )
A. B. C. D.
7.(本题3分)下列关于不等式的命题正确的是( )
A.如果,,那么 B.如果,那么
C.如果,那么 D.如果,那么
8.(本题3分)若关于x的一元一次方程有正整数解,则符合条件的整数的最小值为( )
A.3 B.4 C.5 D.8
9.(本题3分)甲乙两人去超市购物,超市正在举办摸彩活动,单次消费金额每满元可以拿到1张摸彩券.已知甲一次购买5盒饼干拿到3张摸彩券;乙一次购买5盒饼干与1个蛋糕拿到4张摸彩券,若每盒饼干的售价为x元,每个蛋糕的售价为元,则x的取值范围是( )
A. B. C. D.
10.(本题3分)某超市从水果生产基地购进一批水果,运输过程中将会有的损耗,假如不计超市其他费用,如果超市要想至少获得的利润,那么这种水果的售价在进价的基础上应至少提高( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)用不等式表示减去大于: .
12.(本题3分)一部电梯的额定限载量为1000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,货物每箱的质量为50千克,则他们每次最多只能搬运重物 箱.
13.(本题3分)不等式的解集是 .
14.(本题3分)写出一个的值,使大于,则这个的值可以是 .
15.(本题3分)已知,则 (填“>”或“<”).
16.(本题3分)不等式的负整数解有 个.
17.(本题3分)关于的不等式组的解集是 .
18.(本题3分)如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数的值为 .
评卷人得分
三、解答题(共66分)
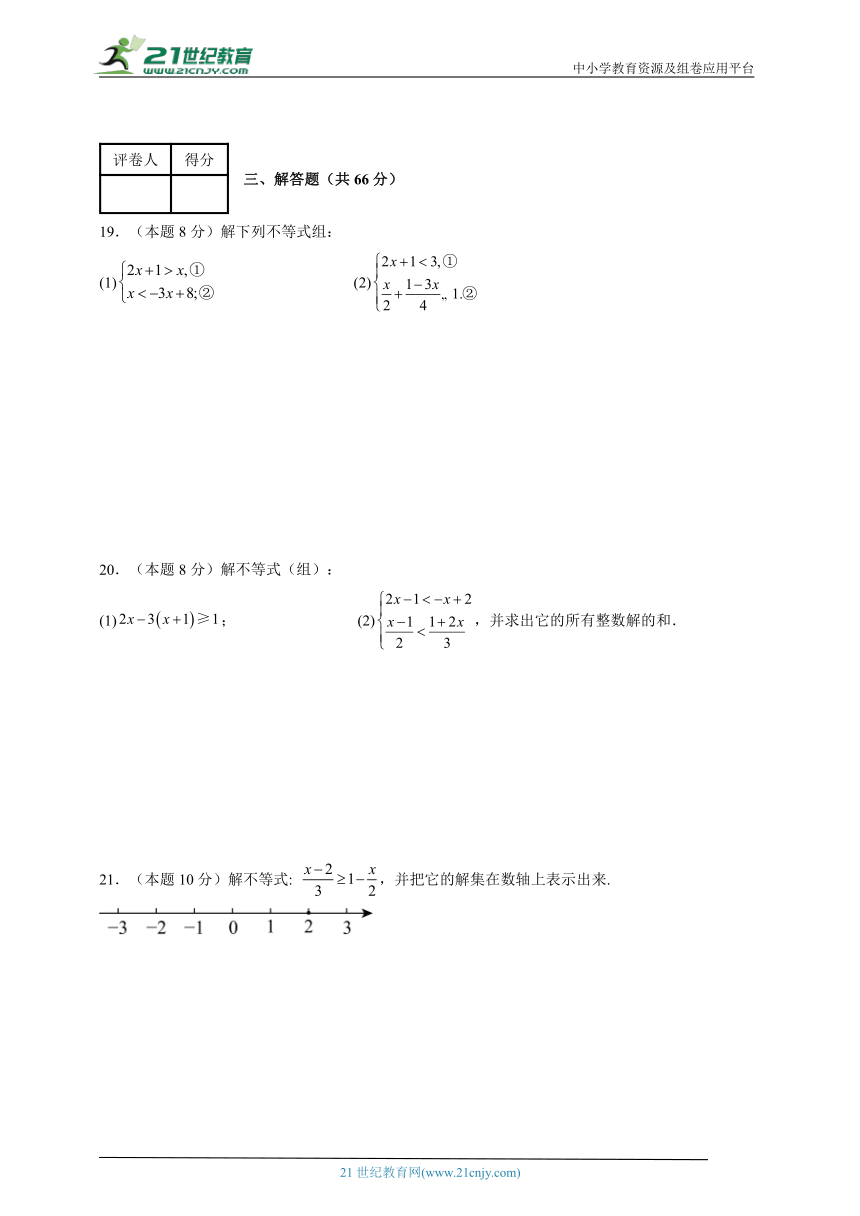
19.(本题8分)解下列不等式组:
(1) (2)
20.(本题8分)解不等式(组):
(1); (2),并求出它的所有整数解的和.
21.(本题10分)解不等式: ,并把它的解集在数轴上表示出来.
22.(本题10分)某小区为了绿化环境,计划购买甲,乙两种花卉共100株,甲种花卉每株15元,乙种花卉每株9元,若购买甲、乙两种花卉的总费用不超过1200元,最多能购买甲种花卉多少株?
23.(本题10分)一个两位数,十位上的数字为m,个位上的数字为n,如果把这个两位数的个位与十位上的数字对调,得到的新两位数大于原来的两位数,请比较m、n的大小.
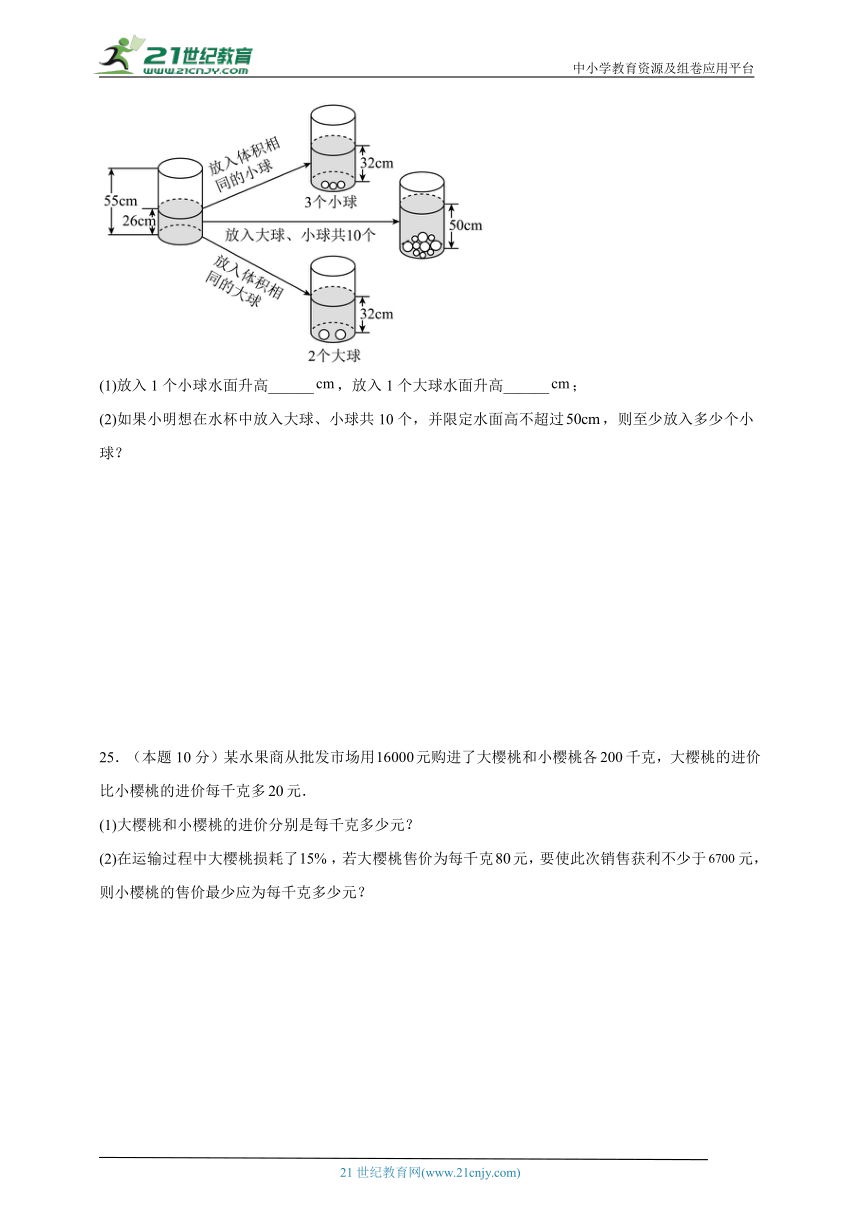
24.(本题10分)小明受《乌鸦喝水》故事的启发,利用水杯、大球和小球进行了如下操作.请根据图中给出的信息,解答下列问题:
(1)放入1个小球水面升高______,放入1个大球水面升高______;
(2)如果小明想在水杯中放入大球、小球共10个,并限定水面高不超过,则至少放入多少个小球?
25.(本题10分)某水果商从批发市场用元购进了大樱桃和小樱桃各千克,大樱桃的进价比小樱桃的进价每千克多元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?
(2)在运输过程中大樱桃损耗了,若大樱桃售价为每千克元,要使此次销售获利不少于元,则小樱桃的售价最少应为每千克多少元?
参考答案:
1.A
【分析】本题考查的是非负数的性质,熟知任意一个数的偶次方都是非负数是解题的关键.根据非负数的性质解答即可.
【详解】解:为实数且,
,
.
故选:A.
2.B
【分析】根据不等式的性质1,在不等式两边同时,即可得到不等式的解集,在数轴上表示不等式的解集,即可得出结果,本题考查了解不等式,在数轴上表示不等式的解集.
【详解】解:,解得:,
不等式的解集在数轴上表示如下:
选项符合,
故选:.
3.D
【分析】本题考查求不等式的解集,掌握解不等式的步骤,正确的计算,是解题的关键,按照解不等式的步骤,进行求解即可.
【详解】解:,
∴,
∴;
故选:D.
4.B
【分析】本题主要考查一元一次不等式的应用.设售价可以按标价打折,根据“每件衣服的利润不低于”即可列出不等式.
【详解】解:按标价打折出售,根据题意,得
.
故选:B.
5.A
【分析】本题考查解一元一次不等式,数轴表示不等式.根据题意将不等式解出,再利用数轴表示即可.
【详解】解:,
即:,,
∴ ,
故选:A.
6.C
【分析】本题考查了不等式的性质,根据不等式的性质逐项求解即可,解题的关键是正确理解不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
【详解】、∵,∴,此选项变形不正确,此选项不符合题意;
、∵,∴,此选项变形不正确,此选项不符合题意;
、∵,∴,此选项变形正确,此选项符合题意;
、∵,∴,此选项变形不正确,此选项不符合题意;
故选:.
7.D
【分析】本题考查了不等式的性质:传递性、性质:同时加上或减去同一个数,不等式的符号不变;同时乘上或除以不等于0的正数,不等式的符号不变;同时乘上或除以不等于0的负数,不等式的符号改变,据此逐项分析,即可作答.
【详解】解:A、如果,,那么的大小关系不确定,该选项是错误的;
B、如果,且,那么,故该选项是错误的;
C、如果,且,那么,故该选项是错误的;
D、如果,那么,故该选项是正确的;
故选:D
8.A
【分析】此题考查了一元一次方程的解,方程去分母,去括号,移项合并,把系数化为1,表示出方程的解,由方程的解为正整数,列不等式,结合为整数得出的所有值,取最小值即可得答案.正确表示出方程的解是解题关键.
【详解】解:
去分母得:,
移项、合并同类项得:,
系数化为1得:,
∵一元一次方程有正整数解,
∴,
∴的值为、、、,
∵为整数,
∴的值为、、、,
∴整数的最小值为,
故选:A.
9.C
【分析】本题考查用不等式组解决实际应用问题,根据彩券数量得到费用区间列不等式组求解即可得到答案;
【详解】解:由题意得,
,
解得:,
故选:C.
10.A
【分析】本题考查的知识点是一元一次不等式的应用,找出题目中的不等关系是解此题的关键,要抓住题目中的关键字,如“大于”、“小于”、“不大于”、“至少”、“不超过”等.设购进这种水果a千克,进价为b元/千克,这种水果的售价在进价的基础上应提高x,则售价为元/千克,根据题意列不等式求解即可.
【详解】解:设购进这种水果a千克,进价为b元/千克,这种水果的售价在进价的基础上应提高x,则售价为元/千克,
根据题意得:购进这批水果用去元,但在售出时,水果只剩下千克,
售货款为元,
根据公式:利润率=(售货款-进货款)÷进货款可列出不等式:
,解得.
故选:A.
11.
【分析】本题主要考查不等式,根据不等式的定义(用“>”或“<”表示不等关系的式子叫做不等式)即可求得答案.
【详解】用不等式表示减去大于为:.
故答案为:.
12.17
【分析】本题考查了由实际问题抽象出一元一次不等式,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
【详解】解:设可以搬运货物箱.
根据题意得,,
解得,
为正整数,
最大为17.
故答案为:17.
13.
【分析】本题考查解一元一次不等式.移项,合并同类项,系数化为1,即可得到答案.
【详解】解:,
移项,合并得,
系数化为1,得.
故答案为:.
14.1(即可)
【分析】本题考查了一元一次不等式的求解,根据题意得,据此即可求解.
【详解】解:由题意得:,
解得:
故答案为:1(即可)
15.
【分析】本题主要考查了不等式的基本性质,解题的关键是掌握不等式的基本性质.利用不等式的基本性质求解即可.
【详解】解:,
,
故答案为:.
16.4
【分析】本题考查了解一元一次不等式.直接求出不等式的解集,然后求出负整数解的个数即可.
【详解】解:∵,
∴,
∴,
∴原不等式的负整数解有:,共4个;
故答案为:4.
17./
【分析】本题考查了解不等式组,分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【详解】解:由,得,
由,得,
∴不等式组的解集是,
故答案为:.
18.或/2或1
【分析】此题考查了一元一次不等式组的应用,根据每一列所有数之和分别为,每一行所有数之和分别为,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案,解题的关键是读懂题意,根据题目中的操作要求,列出不等式组.
【详解】解:∵每一列所有数之和分别为,每一行所有数之和分别为,
则操作第三列,第一行之和为,第二行之和为,
由题意可得,
解得,
∵为整数,
∴或,
故答案为:或.
19.(1)
(2)
【详解】(1)解不等式①,得.
解不等式②,得.
所以原不等式组的解集是.
(2)解不等式①,得.
解不等式②,得.
所以原不等式组的解集为.
20.(1)
(2)
【分析】本题考查了一元一次不等式及一元一次不等式组的求解.注意计算的准确性.
(1)去括号,移项,合并同类项,最后把未知数的系数化为“1”即可;
(2)分别解不等式组中的两个不等式,再取两个解集的公共部分即可.
【详解】(1)解:,
去括号得:,
移项得:,
合并得:,
解得:;
(2)解:
由①得:,
由②得:,
∴不等式组的解集为:,
所有数解的和:.
21.,数轴见解析
【分析】本题考查的是解一元一次不等式,先去分母,再去括号,移项,合并同类项,把的系数化为1,再把不等式的解集在数轴上表示出来即可.
【详解】解:
22.50株
【分析】本题考查一元一次不等式的实际应用,设购买甲种花卉x株,则购买乙种花卉株,根据总费用不超过1200元列一元一次不等式,求出不等式的最大整数解即可.
【详解】解:设购买甲种花卉x株,
由题意得,,
解得,
故最多能购买甲种花卉50株.
23.
【分析】本题考查一元一次不等式的应用,用含m,n的式子表示出原两位数、新两位数,列出不等式,解不等式即可.
【详解】解:由题意知,
移项,得,
合并同类项,得,
解得.
24.(1),
(2)个
【分析】本题考查一元一次不等式的应用,找准数量关系列不等式是解题的关键.
(1)根据3个小球使水位升高了,2个大球使水位升高了进行解答;
(2)设应该放入x个大球,y个小球,根据图示中的关系列不等式,并解答.
【详解】(1)解:放入1个小球水面升高,
放入1个大球水面升高,
故答案为:,;
(2)解:放入个小球,则
,
解得:,
∴至少放入个小球.
25.(1);
(2)小樱桃售价至少元/千克.
【分析】本题考查了方程的实际应用以及一元一次不等式的应用,解题的关键是找准等量关系,正确列出方程,根据各数量之间的关系,正确列出一元一次不等式.
(1)设小樱桃进价元/千克,则大樱桃进价元/千克,列出方程,求解即可;
(2)设小樱桃售价元/千克,列出不等式求解即可.
【详解】(1)解:设小樱桃进价元/千克,则大樱桃进价元/千克
解得,,
∴.
(2)解:设小樱桃售价元/千克,
,
解得
答:小樱桃售价至少元/千克.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级一元一次不等式和一元一次不等式组(京改版)单元测试 基础卷一 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)已知为实数且,则下列各式一定成立的是( )
A. B. C. D.
2.(本题3分)在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
3.(本题3分)不等式的解集是( )
A. B. C. D.
4.(本题3分)亚运会期间,某商店购进了一批服装,每件进价为元,并以每件元的价格出售,亚运会结束后,商店准备将这批服装降价处理,打折出售,使得每件衣服的利润不低于,根据题意可列出来的不等式为( )
A. B.
C. D.
5.(本题3分)不等式的解集表示在数轴上,你认为正确的是( )
A. B.
C.
D.
6.(本题3分)已知,下列不等式变形中正确的是( )
A. B. C. D.
7.(本题3分)下列关于不等式的命题正确的是( )
A.如果,,那么 B.如果,那么
C.如果,那么 D.如果,那么
8.(本题3分)若关于x的一元一次方程有正整数解,则符合条件的整数的最小值为( )
A.3 B.4 C.5 D.8
9.(本题3分)甲乙两人去超市购物,超市正在举办摸彩活动,单次消费金额每满元可以拿到1张摸彩券.已知甲一次购买5盒饼干拿到3张摸彩券;乙一次购买5盒饼干与1个蛋糕拿到4张摸彩券,若每盒饼干的售价为x元,每个蛋糕的售价为元,则x的取值范围是( )
A. B. C. D.
10.(本题3分)某超市从水果生产基地购进一批水果,运输过程中将会有的损耗,假如不计超市其他费用,如果超市要想至少获得的利润,那么这种水果的售价在进价的基础上应至少提高( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)用不等式表示减去大于: .
12.(本题3分)一部电梯的额定限载量为1000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,货物每箱的质量为50千克,则他们每次最多只能搬运重物 箱.
13.(本题3分)不等式的解集是 .
14.(本题3分)写出一个的值,使大于,则这个的值可以是 .
15.(本题3分)已知,则 (填“>”或“<”).
16.(本题3分)不等式的负整数解有 个.
17.(本题3分)关于的不等式组的解集是 .
18.(本题3分)如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数的值为 .
评卷人得分
三、解答题(共66分)
19.(本题8分)解下列不等式组:
(1) (2)
20.(本题8分)解不等式(组):
(1); (2),并求出它的所有整数解的和.
21.(本题10分)解不等式: ,并把它的解集在数轴上表示出来.
22.(本题10分)某小区为了绿化环境,计划购买甲,乙两种花卉共100株,甲种花卉每株15元,乙种花卉每株9元,若购买甲、乙两种花卉的总费用不超过1200元,最多能购买甲种花卉多少株?
23.(本题10分)一个两位数,十位上的数字为m,个位上的数字为n,如果把这个两位数的个位与十位上的数字对调,得到的新两位数大于原来的两位数,请比较m、n的大小.
24.(本题10分)小明受《乌鸦喝水》故事的启发,利用水杯、大球和小球进行了如下操作.请根据图中给出的信息,解答下列问题:
(1)放入1个小球水面升高______,放入1个大球水面升高______;
(2)如果小明想在水杯中放入大球、小球共10个,并限定水面高不超过,则至少放入多少个小球?
25.(本题10分)某水果商从批发市场用元购进了大樱桃和小樱桃各千克,大樱桃的进价比小樱桃的进价每千克多元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?
(2)在运输过程中大樱桃损耗了,若大樱桃售价为每千克元,要使此次销售获利不少于元,则小樱桃的售价最少应为每千克多少元?
参考答案:
1.A
【分析】本题考查的是非负数的性质,熟知任意一个数的偶次方都是非负数是解题的关键.根据非负数的性质解答即可.
【详解】解:为实数且,
,
.
故选:A.
2.B
【分析】根据不等式的性质1,在不等式两边同时,即可得到不等式的解集,在数轴上表示不等式的解集,即可得出结果,本题考查了解不等式,在数轴上表示不等式的解集.
【详解】解:,解得:,
不等式的解集在数轴上表示如下:
选项符合,
故选:.
3.D
【分析】本题考查求不等式的解集,掌握解不等式的步骤,正确的计算,是解题的关键,按照解不等式的步骤,进行求解即可.
【详解】解:,
∴,
∴;
故选:D.
4.B
【分析】本题主要考查一元一次不等式的应用.设售价可以按标价打折,根据“每件衣服的利润不低于”即可列出不等式.
【详解】解:按标价打折出售,根据题意,得
.
故选:B.
5.A
【分析】本题考查解一元一次不等式,数轴表示不等式.根据题意将不等式解出,再利用数轴表示即可.
【详解】解:,
即:,,
∴ ,
故选:A.
6.C
【分析】本题考查了不等式的性质,根据不等式的性质逐项求解即可,解题的关键是正确理解不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
【详解】、∵,∴,此选项变形不正确,此选项不符合题意;
、∵,∴,此选项变形不正确,此选项不符合题意;
、∵,∴,此选项变形正确,此选项符合题意;
、∵,∴,此选项变形不正确,此选项不符合题意;
故选:.
7.D
【分析】本题考查了不等式的性质:传递性、性质:同时加上或减去同一个数,不等式的符号不变;同时乘上或除以不等于0的正数,不等式的符号不变;同时乘上或除以不等于0的负数,不等式的符号改变,据此逐项分析,即可作答.
【详解】解:A、如果,,那么的大小关系不确定,该选项是错误的;
B、如果,且,那么,故该选项是错误的;
C、如果,且,那么,故该选项是错误的;
D、如果,那么,故该选项是正确的;
故选:D
8.A
【分析】此题考查了一元一次方程的解,方程去分母,去括号,移项合并,把系数化为1,表示出方程的解,由方程的解为正整数,列不等式,结合为整数得出的所有值,取最小值即可得答案.正确表示出方程的解是解题关键.
【详解】解:
去分母得:,
移项、合并同类项得:,
系数化为1得:,
∵一元一次方程有正整数解,
∴,
∴的值为、、、,
∵为整数,
∴的值为、、、,
∴整数的最小值为,
故选:A.
9.C
【分析】本题考查用不等式组解决实际应用问题,根据彩券数量得到费用区间列不等式组求解即可得到答案;
【详解】解:由题意得,
,
解得:,
故选:C.
10.A
【分析】本题考查的知识点是一元一次不等式的应用,找出题目中的不等关系是解此题的关键,要抓住题目中的关键字,如“大于”、“小于”、“不大于”、“至少”、“不超过”等.设购进这种水果a千克,进价为b元/千克,这种水果的售价在进价的基础上应提高x,则售价为元/千克,根据题意列不等式求解即可.
【详解】解:设购进这种水果a千克,进价为b元/千克,这种水果的售价在进价的基础上应提高x,则售价为元/千克,
根据题意得:购进这批水果用去元,但在售出时,水果只剩下千克,
售货款为元,
根据公式:利润率=(售货款-进货款)÷进货款可列出不等式:
,解得.
故选:A.
11.
【分析】本题主要考查不等式,根据不等式的定义(用“>”或“<”表示不等关系的式子叫做不等式)即可求得答案.
【详解】用不等式表示减去大于为:.
故答案为:.
12.17
【分析】本题考查了由实际问题抽象出一元一次不等式,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
【详解】解:设可以搬运货物箱.
根据题意得,,
解得,
为正整数,
最大为17.
故答案为:17.
13.
【分析】本题考查解一元一次不等式.移项,合并同类项,系数化为1,即可得到答案.
【详解】解:,
移项,合并得,
系数化为1,得.
故答案为:.
14.1(即可)
【分析】本题考查了一元一次不等式的求解,根据题意得,据此即可求解.
【详解】解:由题意得:,
解得:
故答案为:1(即可)
15.
【分析】本题主要考查了不等式的基本性质,解题的关键是掌握不等式的基本性质.利用不等式的基本性质求解即可.
【详解】解:,
,
故答案为:.
16.4
【分析】本题考查了解一元一次不等式.直接求出不等式的解集,然后求出负整数解的个数即可.
【详解】解:∵,
∴,
∴,
∴原不等式的负整数解有:,共4个;
故答案为:4.
17./
【分析】本题考查了解不等式组,分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【详解】解:由,得,
由,得,
∴不等式组的解集是,
故答案为:.
18.或/2或1
【分析】此题考查了一元一次不等式组的应用,根据每一列所有数之和分别为,每一行所有数之和分别为,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案,解题的关键是读懂题意,根据题目中的操作要求,列出不等式组.
【详解】解:∵每一列所有数之和分别为,每一行所有数之和分别为,
则操作第三列,第一行之和为,第二行之和为,
由题意可得,
解得,
∵为整数,
∴或,
故答案为:或.
19.(1)
(2)
【详解】(1)解不等式①,得.
解不等式②,得.
所以原不等式组的解集是.
(2)解不等式①,得.
解不等式②,得.
所以原不等式组的解集为.
20.(1)
(2)
【分析】本题考查了一元一次不等式及一元一次不等式组的求解.注意计算的准确性.
(1)去括号,移项,合并同类项,最后把未知数的系数化为“1”即可;
(2)分别解不等式组中的两个不等式,再取两个解集的公共部分即可.
【详解】(1)解:,
去括号得:,
移项得:,
合并得:,
解得:;
(2)解:
由①得:,
由②得:,
∴不等式组的解集为:,
所有数解的和:.
21.,数轴见解析
【分析】本题考查的是解一元一次不等式,先去分母,再去括号,移项,合并同类项,把的系数化为1,再把不等式的解集在数轴上表示出来即可.
【详解】解:
22.50株
【分析】本题考查一元一次不等式的实际应用,设购买甲种花卉x株,则购买乙种花卉株,根据总费用不超过1200元列一元一次不等式,求出不等式的最大整数解即可.
【详解】解:设购买甲种花卉x株,
由题意得,,
解得,
故最多能购买甲种花卉50株.
23.
【分析】本题考查一元一次不等式的应用,用含m,n的式子表示出原两位数、新两位数,列出不等式,解不等式即可.
【详解】解:由题意知,
移项,得,
合并同类项,得,
解得.
24.(1),
(2)个
【分析】本题考查一元一次不等式的应用,找准数量关系列不等式是解题的关键.
(1)根据3个小球使水位升高了,2个大球使水位升高了进行解答;
(2)设应该放入x个大球,y个小球,根据图示中的关系列不等式,并解答.
【详解】(1)解:放入1个小球水面升高,
放入1个大球水面升高,
故答案为:,;
(2)解:放入个小球,则
,
解得:,
∴至少放入个小球.
25.(1);
(2)小樱桃售价至少元/千克.
【分析】本题考查了方程的实际应用以及一元一次不等式的应用,解题的关键是找准等量关系,正确列出方程,根据各数量之间的关系,正确列出一元一次不等式.
(1)设小樱桃进价元/千克,则大樱桃进价元/千克,列出方程,求解即可;
(2)设小樱桃售价元/千克,列出不等式求解即可.
【详解】(1)解:设小樱桃进价元/千克,则大樱桃进价元/千克
解得,,
∴.
(2)解:设小樱桃售价元/千克,
,
解得
答:小樱桃售价至少元/千克.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
