1.3同底数幂的除法 第2课时 课件(共24张PPT)-2023-2024学年七年级数学下册同步课件(北师大版)
文档属性
| 名称 | 1.3同底数幂的除法 第2课时 课件(共24张PPT)-2023-2024学年七年级数学下册同步课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 504.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第2课时
北师大版 数学 七年级下册
3 同底数幂的除法
第一章 整式的乘除
学习目标
1.会用科学记数法表示绝对值小于1的数.(重点)
2.会用科学记数法解决相应的实际问题.(难点)
3.负整数指数幂: (a≠0,n为正整数).
1.同底数幂的除法法则:am ÷ an = (a≠0,m,n都是正整数,且m>n).同底数幂相除,底数 ,指数 .
一、导入新课
复习回顾
不变
相减
am-n
2.零指数幂:任何不等于零的数的零次幂都等于 .
即a0= (a≠0).
1
1
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.例如,864000可以写成 .
8.64×105
想一想:你还记得科学记数法吗?
一、导入新课
情境导入
怎样把以上这些较小的数用科学记数法表示呢?
问题:你知道一粒花粉直径是多少吗?一根头发的直径又是多少?
无论是在生活中或学习中,我们都会遇到一些较小的数,例如,
细胞的直径只有1微米(m),即0.000 001m;
某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s;
一个氧原子的质量为0.000 000 000 000 000 000 000 000 026 57kg.
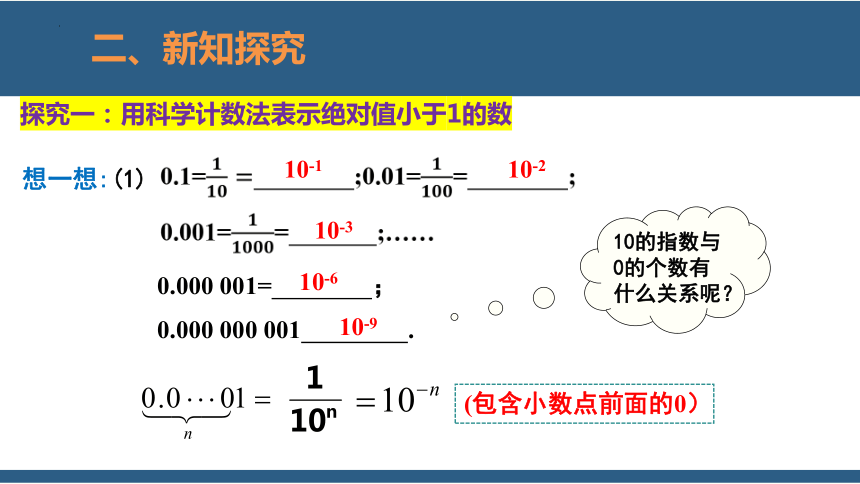
想一想:(1)
0.1= ;0.01== ;
0.001== ;……
0.000 001= ;
0.000 000 001 .
二、新知探究
探究一:用科学计数法表示绝对值小于1的数
10-1
10-2
10-3
10-6
10-9
(包含小数点前面的0)
10的指数与0的个数有什么关系呢?
二、新知探究
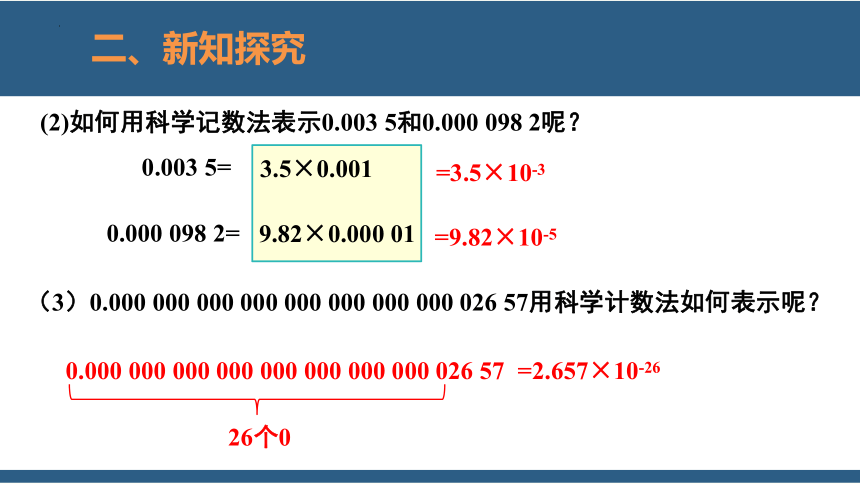
(2)如何用科学记数法表示0.003 5和0.000 098 2呢?
0.003 5=
3.5×0.001
0.000 098 2=
9.82×0.000 01
=3.5×10-3
=9.82×10-5
(3)0.000 000 000 000 000 000 000 000 026 57用科学计数法如何表示呢?
=2.657×10-26
0.000 000 000 000 000 000 000 000 026 57
26个0
二、新知探究
知识归纳
怎样确定a和n?
a×10n,其中1≤a<10,n是负整数.
一般地,一个小于1的正数可以用科学记数法表示为:
用科学计数法表示绝对值小于1的数的方法:
a和n值的确定:
(1)a的确定方法:整数部分只含一位的数(即1≤a<10);
(2)n的确定方法:n由原数左起第一个不为零的数字前面的0的个数所决定(特别注意:包括小数点前面这个零).
做一做:
用科学记数法表示下列各数:
(1)0.000 000 0001= ,
(2)0.000 000 000 0029= ,
(3)0.000 000 001 295= .
二、新知探究
1×10-10
2.9×10-12
1.295×10-9
思考:-0.000 000 000 005 96如何用科学记数法表示?
-5.96×10-12
注意:大于-1的负数也可以用科学记数法表示,只是多一个负号,记作-a×10n.其中1≤a<10,n是负整数.
二、新知探究
跟踪练习
1.用科学记数法表示:
(1)0.000 03= ;
(2)-0.000 006 4= ;
(3)0.000 0314= ;
(4)0.000 000 000 342 5= .
3×10-5
-6.4×10-6
3.14×10-5
3.425×10-10
二、新知探究
想一想:(1)你能把下列数还原为小数表示吗?
10-2= ___________; 10-4= ___________;
10-8= ___________.
(2)指数与运算结果的0的个数有什么关系?通过上面的探索,你发现了什么?
一般地,10的-n次幂,还原为小数时,在1前面有_____个0.
(3)10-21的小数点后的位数是几位?1前面有几个零?
0.01
0.0001
0.00000001
n
21位
二、新知探究
2.用小数表示下列各数:
(1)7×10-5; (2)1.35×10-10; (3)2.657×10-16; (4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)7×10-5=0.000 07;
(2)1.35×10-10=0.000 000 000 135;
(3)2.657×10-16=0.000 000 000 000 000 265 7;
(4)2.17×10-1=0.217.
跟踪练习
把用科学记数法表示的绝对值小于1的数还原时,除了数0法,还可以运用以下方法:看指数的绝对值是几,小数点就向左移动几位.
二、新知探究
探究二:科学记数法在实际生活中的应用
(2)方法一:1÷(2.5×10-6)=4×105(个).
方法二:1000000÷2.5=4×105(个).
议一议:1.PM2.5是指大气中直径小于或等于2.5 μm的细颗粒物,也称为可入肺颗粒物.虽然它们的直径还不到人的头发粗细的,但它们含有大量的有毒、有害物质,并且在大气中的停留时间长、输送距离远,因而对人体健康和大气环境质量有很大的危害.
(1)假设一种可入肺颗粒物的直径约为2.5 μm,相当于多少米
(2)多少个这样的细颗粒物首尾连接起来能达到1 m 与同伴进行交流.
(1)因为1m=1 000 000 μm,
所以1μm=m=10-6m,
所以2.5μm=2.5×10-6m.
二、新知探究
2.估计1张纸的厚度大约是多少厘米.你是怎样做的 与同伴进行交流.
解:可以通过测量100张纸的厚度,然后再用总的厚度除以100得到每张纸的厚度.
用科学记数法表示一些单位换算问题
单位换算:
(1)1纳米=10-9米,1微米=10-6,1毫米=10-3米;(2)1平方厘米=10-4平方米,1平方米=10-6平方千米;(3)1毫升=10-6立方米.
二、新知探究
3.原子弹的原料——铀,每克含有2.56×1021个原子核,一个原子核裂变时能放出3.2×10-11 J的热量,那么每克铀全部裂变时能放出多少热量
解:由题意得2.56×1021×3.2×10-11
=2.56×3.2×1021×10-11
=8.192×1010(J).
故每克铀全部裂变时能放出8.192×1010 J的热量.
跟踪练习
三、典例精析
例1:把下列各数用科学记数法表示.
(1)0.00002; (2)0.000707;
(3)-0.000122; (4)0.000056.
解:(1)0.00002=2×10- 5; (2)0.000707=7.07×10- 4.
(3)-0.000122=-1.22×10- 4. (4)0.000056=5.6×10- 5.
三、典例精析
例2:用小数表示下列各数.
(1)-6.23×10-5;
(2)(-2)3×10-8.
解:(1)-6.23×10-5=-0.0000623.
(2)(-2)3×10-8=-8×10-8=-0.00000008.
三、典例精析
例3:1块900 mm2的芯片上能集成10亿个元件,每一个这样的元件约占多少平方毫米 约多少平方米 (用科学记数法表示)
解:=900×10-9
=9×10-7(mm2)
=9×10-13(m2).故每一个这样的元件约占9×10-7mm2,约9×10-13 m2.
2.已知某种新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )
A.8.23×10-6 B.8.23×10-7 C.8.23×106 D.8.23×107
3.-0.00035用科学记数法表示为( )
A.-3.5×10-4 B.-3.5×104
C.3.5×10-4 D.-3.5×10-3
四、当堂练习
1.某种计算机完成一次基本运算的时间约为0.000000001 s,把0.000000001 s用科学记数法可以表示为 ( )
A.0.1×10- 8 s B.0.1×10- 9 s C.1×10- 8 s D.1×10- 9 s
D
B
A
四、当堂练习
4.将6.18×10-3化为小数是 ( )
A.0.000618 B.0.00618 C.0.0618 D.0.618
B
5.把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为 ( )
A.1 B.-2 C.0.813 D.8.13
D
6.某景区五一小长假期间购票进山游客12万人次,再创历史新高.景区门票价格旺季168元/人,以此计算,五一小长假期间,景区门票总收入用科学记数法表示为( )
A.2.016×108元 B.0.2016×107元
C.2.016×107元 D.2016×104元
C
四、当堂练习
7.用科学记数法表示下列各数:
(1)0.000023= ;
(2)0.000000802= ;
(3)-0.0000002022= .
2.3×10-5
8.02×10-7
-2.022×10-7
8.某颗粒物的直径是0.0000025米,把0.0000025用科学记数法表示为
.
4×10-3
2.5×10-6
9.据测算,5万粒芝麻的质量约为200 g,那么一粒芝麻的质量约为
g.(用科学记数法表示)
四、当堂练习
10.用小数表示下列各数.
(1)2.6×10-5; (2)3.79×10-6; (3)-2.09×10-8.
解:(1)2.6×10-5=0.000026.
(2)3.79×10-6=0.00000379.
(3)-2.09×10-8=-0.0000000209.
11.一个正方体集装箱的棱长为0.8 m.
(1)这个集装箱的体积是多少(用科学记数法表示)
(2)若有一个小立方块的棱长为2×10-2 m,则需要多少个这样的小立方块才能将这个集装箱装满
解:(1)0.83=0.512(m3)=5.12×10-1 (m3).
故这个集装箱的体积是5.12×10-1 m3.
(2)(2×10-2)3=8×10-6(m3).(5.12×10-1)÷(8×10-6)=6.4×104(个).
故需要6.4×104个这样的小立方块才能将这个集装箱装满.
四、当堂练习
五、课堂小结
把科学记数法表示的小数还原成原数
同底数幂的除法2
用科学记数法表示小数
一般地,一个小于1的正数可以用科学记数法表示为:a×10n,其中1≤a<10,n是负整数.
把用科学记数法表示的绝对值小于1的数还原时,除了数0法,还可以运用以下方法:看指数的绝对值是几,小数点就向左移动几位.
科学计数法的应用
常见单位换算:(1)1纳米=10-9米,1微米=10-6,1毫米=10-3米;(2)1平方厘米=10-4平方米,1平方米=10-6平方千米;(3)1毫升=10-6立方米.
六、作业布置
习题1.5
第2课时
北师大版 数学 七年级下册
3 同底数幂的除法
第一章 整式的乘除
学习目标
1.会用科学记数法表示绝对值小于1的数.(重点)
2.会用科学记数法解决相应的实际问题.(难点)
3.负整数指数幂: (a≠0,n为正整数).
1.同底数幂的除法法则:am ÷ an = (a≠0,m,n都是正整数,且m>n).同底数幂相除,底数 ,指数 .
一、导入新课
复习回顾
不变
相减
am-n
2.零指数幂:任何不等于零的数的零次幂都等于 .
即a0= (a≠0).
1
1
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.例如,864000可以写成 .
8.64×105
想一想:你还记得科学记数法吗?
一、导入新课
情境导入
怎样把以上这些较小的数用科学记数法表示呢?
问题:你知道一粒花粉直径是多少吗?一根头发的直径又是多少?
无论是在生活中或学习中,我们都会遇到一些较小的数,例如,
细胞的直径只有1微米(m),即0.000 001m;
某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s;
一个氧原子的质量为0.000 000 000 000 000 000 000 000 026 57kg.
想一想:(1)
0.1= ;0.01== ;
0.001== ;……
0.000 001= ;
0.000 000 001 .
二、新知探究
探究一:用科学计数法表示绝对值小于1的数
10-1
10-2
10-3
10-6
10-9
(包含小数点前面的0)
10的指数与0的个数有什么关系呢?
二、新知探究
(2)如何用科学记数法表示0.003 5和0.000 098 2呢?
0.003 5=
3.5×0.001
0.000 098 2=
9.82×0.000 01
=3.5×10-3
=9.82×10-5
(3)0.000 000 000 000 000 000 000 000 026 57用科学计数法如何表示呢?
=2.657×10-26
0.000 000 000 000 000 000 000 000 026 57
26个0
二、新知探究
知识归纳
怎样确定a和n?
a×10n,其中1≤a<10,n是负整数.
一般地,一个小于1的正数可以用科学记数法表示为:
用科学计数法表示绝对值小于1的数的方法:
a和n值的确定:
(1)a的确定方法:整数部分只含一位的数(即1≤a<10);
(2)n的确定方法:n由原数左起第一个不为零的数字前面的0的个数所决定(特别注意:包括小数点前面这个零).
做一做:
用科学记数法表示下列各数:
(1)0.000 000 0001= ,
(2)0.000 000 000 0029= ,
(3)0.000 000 001 295= .
二、新知探究
1×10-10
2.9×10-12
1.295×10-9
思考:-0.000 000 000 005 96如何用科学记数法表示?
-5.96×10-12
注意:大于-1的负数也可以用科学记数法表示,只是多一个负号,记作-a×10n.其中1≤a<10,n是负整数.
二、新知探究
跟踪练习
1.用科学记数法表示:
(1)0.000 03= ;
(2)-0.000 006 4= ;
(3)0.000 0314= ;
(4)0.000 000 000 342 5= .
3×10-5
-6.4×10-6
3.14×10-5
3.425×10-10
二、新知探究
想一想:(1)你能把下列数还原为小数表示吗?
10-2= ___________; 10-4= ___________;
10-8= ___________.
(2)指数与运算结果的0的个数有什么关系?通过上面的探索,你发现了什么?
一般地,10的-n次幂,还原为小数时,在1前面有_____个0.
(3)10-21的小数点后的位数是几位?1前面有几个零?
0.01
0.0001
0.00000001
n
21位
二、新知探究
2.用小数表示下列各数:
(1)7×10-5; (2)1.35×10-10; (3)2.657×10-16; (4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)7×10-5=0.000 07;
(2)1.35×10-10=0.000 000 000 135;
(3)2.657×10-16=0.000 000 000 000 000 265 7;
(4)2.17×10-1=0.217.
跟踪练习
把用科学记数法表示的绝对值小于1的数还原时,除了数0法,还可以运用以下方法:看指数的绝对值是几,小数点就向左移动几位.
二、新知探究
探究二:科学记数法在实际生活中的应用
(2)方法一:1÷(2.5×10-6)=4×105(个).
方法二:1000000÷2.5=4×105(个).
议一议:1.PM2.5是指大气中直径小于或等于2.5 μm的细颗粒物,也称为可入肺颗粒物.虽然它们的直径还不到人的头发粗细的,但它们含有大量的有毒、有害物质,并且在大气中的停留时间长、输送距离远,因而对人体健康和大气环境质量有很大的危害.
(1)假设一种可入肺颗粒物的直径约为2.5 μm,相当于多少米
(2)多少个这样的细颗粒物首尾连接起来能达到1 m 与同伴进行交流.
(1)因为1m=1 000 000 μm,
所以1μm=m=10-6m,
所以2.5μm=2.5×10-6m.
二、新知探究
2.估计1张纸的厚度大约是多少厘米.你是怎样做的 与同伴进行交流.
解:可以通过测量100张纸的厚度,然后再用总的厚度除以100得到每张纸的厚度.
用科学记数法表示一些单位换算问题
单位换算:
(1)1纳米=10-9米,1微米=10-6,1毫米=10-3米;(2)1平方厘米=10-4平方米,1平方米=10-6平方千米;(3)1毫升=10-6立方米.
二、新知探究
3.原子弹的原料——铀,每克含有2.56×1021个原子核,一个原子核裂变时能放出3.2×10-11 J的热量,那么每克铀全部裂变时能放出多少热量
解:由题意得2.56×1021×3.2×10-11
=2.56×3.2×1021×10-11
=8.192×1010(J).
故每克铀全部裂变时能放出8.192×1010 J的热量.
跟踪练习
三、典例精析
例1:把下列各数用科学记数法表示.
(1)0.00002; (2)0.000707;
(3)-0.000122; (4)0.000056.
解:(1)0.00002=2×10- 5; (2)0.000707=7.07×10- 4.
(3)-0.000122=-1.22×10- 4. (4)0.000056=5.6×10- 5.
三、典例精析
例2:用小数表示下列各数.
(1)-6.23×10-5;
(2)(-2)3×10-8.
解:(1)-6.23×10-5=-0.0000623.
(2)(-2)3×10-8=-8×10-8=-0.00000008.
三、典例精析
例3:1块900 mm2的芯片上能集成10亿个元件,每一个这样的元件约占多少平方毫米 约多少平方米 (用科学记数法表示)
解:=900×10-9
=9×10-7(mm2)
=9×10-13(m2).故每一个这样的元件约占9×10-7mm2,约9×10-13 m2.
2.已知某种新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )
A.8.23×10-6 B.8.23×10-7 C.8.23×106 D.8.23×107
3.-0.00035用科学记数法表示为( )
A.-3.5×10-4 B.-3.5×104
C.3.5×10-4 D.-3.5×10-3
四、当堂练习
1.某种计算机完成一次基本运算的时间约为0.000000001 s,把0.000000001 s用科学记数法可以表示为 ( )
A.0.1×10- 8 s B.0.1×10- 9 s C.1×10- 8 s D.1×10- 9 s
D
B
A
四、当堂练习
4.将6.18×10-3化为小数是 ( )
A.0.000618 B.0.00618 C.0.0618 D.0.618
B
5.把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为 ( )
A.1 B.-2 C.0.813 D.8.13
D
6.某景区五一小长假期间购票进山游客12万人次,再创历史新高.景区门票价格旺季168元/人,以此计算,五一小长假期间,景区门票总收入用科学记数法表示为( )
A.2.016×108元 B.0.2016×107元
C.2.016×107元 D.2016×104元
C
四、当堂练习
7.用科学记数法表示下列各数:
(1)0.000023= ;
(2)0.000000802= ;
(3)-0.0000002022= .
2.3×10-5
8.02×10-7
-2.022×10-7
8.某颗粒物的直径是0.0000025米,把0.0000025用科学记数法表示为
.
4×10-3
2.5×10-6
9.据测算,5万粒芝麻的质量约为200 g,那么一粒芝麻的质量约为
g.(用科学记数法表示)
四、当堂练习
10.用小数表示下列各数.
(1)2.6×10-5; (2)3.79×10-6; (3)-2.09×10-8.
解:(1)2.6×10-5=0.000026.
(2)3.79×10-6=0.00000379.
(3)-2.09×10-8=-0.0000000209.
11.一个正方体集装箱的棱长为0.8 m.
(1)这个集装箱的体积是多少(用科学记数法表示)
(2)若有一个小立方块的棱长为2×10-2 m,则需要多少个这样的小立方块才能将这个集装箱装满
解:(1)0.83=0.512(m3)=5.12×10-1 (m3).
故这个集装箱的体积是5.12×10-1 m3.
(2)(2×10-2)3=8×10-6(m3).(5.12×10-1)÷(8×10-6)=6.4×104(个).
故需要6.4×104个这样的小立方块才能将这个集装箱装满.
四、当堂练习
五、课堂小结
把科学记数法表示的小数还原成原数
同底数幂的除法2
用科学记数法表示小数
一般地,一个小于1的正数可以用科学记数法表示为:a×10n,其中1≤a<10,n是负整数.
把用科学记数法表示的绝对值小于1的数还原时,除了数0法,还可以运用以下方法:看指数的绝对值是几,小数点就向左移动几位.
科学计数法的应用
常见单位换算:(1)1纳米=10-9米,1微米=10-6,1毫米=10-3米;(2)1平方厘米=10-4平方米,1平方米=10-6平方千米;(3)1毫升=10-6立方米.
六、作业布置
习题1.5
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
