第7章 锐角三角函数(小结与思考)(单元复习课件)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 第7章 锐角三角函数(小结与思考)(单元复习课件)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 08:52:37 | ||
图片预览









文档简介
(共49张PPT)
第7章 锐角三角函数
小结与思考
学习目标
1. 整理本章所学知识,构建本章知识框架;
2. 进一步理解三角函数的概念,明确直角三角形各元素间的关系,进一步学会利用数形结合的思想方法分析问题和解决问题.
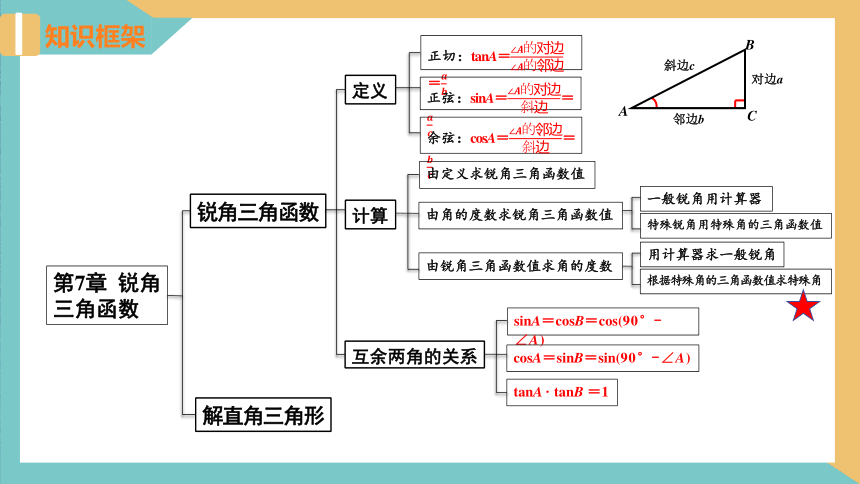
知识框架
第7章 锐角三角函数
锐角三角函数
定义
正切:tanA==
正弦:sinA==
余弦:cosA==
A
B
C
斜边c
对边a
邻边b
计算
由定义求锐角三角函数值
由角的度数求锐角三角函数值
由锐角三角函数值求角的度数
一般锐角用计算器
特殊锐角用特殊角的三角函数值
用计算器求一般锐角
根据特殊角的三角函数值求特殊角
互余两角的关系
sinA=cosB=cos(90°-∠A)
cosA=sinB=sin(90°-∠A)
tanA · tanB =1
解直角三角形
知识框架
第7章 锐角三角函数
解直角三角形
定义
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
依据
三边之间的关系:a2+b2=c2 (勾股定理)
锐角之间的关系: ∠A+ ∠B=90°(直角三角形的两个锐角互余)
边、角之间的关系:sinA=,cosA=,tanA=
基本类型
已知一锐角、一边:一锐角、一直角边或一斜边
已知两边:一直角边,一斜边或者两条直角边
简单应用
与仰角、俯角有关的实际问题
与方向角有关的实际问题
与坡角有关的实际问题
与生活有关的其他实际问题
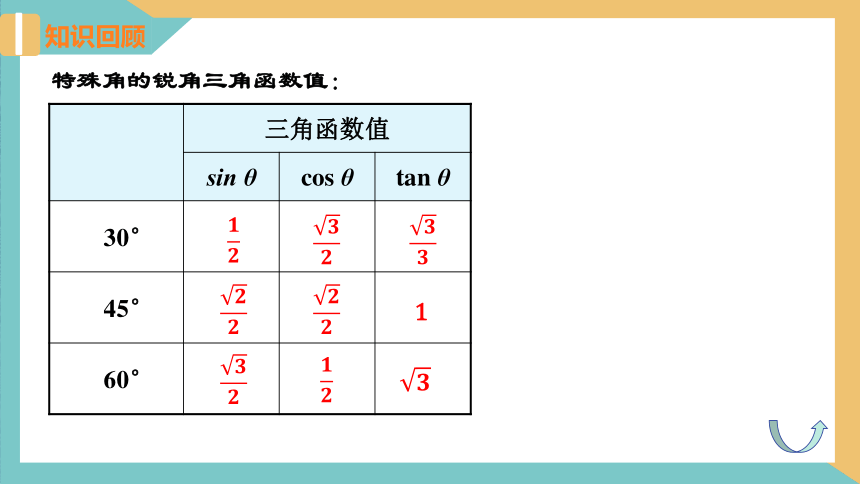
知识回顾
特殊角的锐角三角函数值:
三角函数值 sin θ cos θ tan θ
30°
45°
60°
1
知识回顾
已 知 类 型 已知条件 解 法 步 骤
一边和一锐角 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 斜边和一锐角 (如c,∠A) ①∠B=90°-∠A;
②由sinA=,得a=c·sinA;
③由cosA=,得b=c·cosA
一边和一锐角 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 一直角边和一锐角(如a,∠A) ①∠B=90°-∠A;
②由tanA=,得b=;
③由sinA=,得c=
解直角三角形的基本类型和解法
知识回顾
已 知 类 型 已知条件 解 法 步 骤
两边 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 斜边和一直角边(如c,a) ①b=;
②由sinA=,求∠A;
③∠B=90°-∠A
两直角边 (a,b) ①c=;
②由tanA=,求∠A;
③∠B=90°-∠A
解直角三角形时,选择关系式的原则:
(1)尽量选可以直接应用原始数据的关系式;
(2)设法选择便于计算的关系式,若能用乘法计算就避免用除法计算.
知识回顾
解直角三角形的简单应用
概念 定义 图形
仰角 俯角
坡度(坡 比)、坡角
方向角
仰角
俯角
视线
水平线
o
视线
铅垂线
当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角.
当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角.
α
l
h
A
B
C
坡面的垂直高度h与水平宽度l的比叫做坡度(坡比),用字母i表示;坡面与水平面的夹角α叫坡角,i=tanα=.
方向角一般是以观测者的位置为中心,将正北(或正南)方向作为起始方向依顺时针(或逆时针)方向到目标方向线之间的锐角.
东
北
O
45°
E
M
25°
60°
N
考点分析
例1 如图,在Rt△ABC中,∠C=90°,BC=6,tanA=. 求AB的长和sinB的值.
B
A
C
6
解:∵在Rt△ABC中,∠C=90°,BC=6,
tanA==,
∴AC=12,
∴AB===6
∴sinB===.
考点一 锐角三角函数的定义
巩固练习
1. 已知等腰三角形的三边长之比为1:1:,则它的顶角为( )
A. 150° B. 120° C. 60° D. 30°
B
2. 在△ABC中,∠C=90°,若sinB+cosA=1,则∠B的度数是( )
A. 60° B. 45° C. 30° D. 不能确定
C
巩固练习
3.(2022·扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边. 若b2=ac,则sin A的值为 .
4.(2023·江苏)如图,在中,,点D在边AB上,连接CD.若,,则______.
B
D
A
C
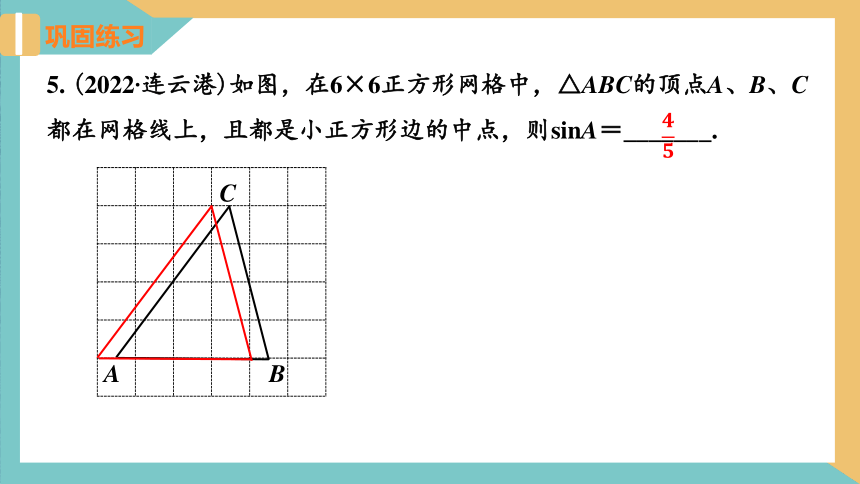
5. (2022·连云港)如图,在6×6正方形网格中,△ABC的顶点A、B、C都在网格线上,且都是小正方形边的中点,则sinA=_______.
A
B
C
巩固练习
解:过点D作DE⊥BC,垂足为E.易得四边形ABED是矩形,BE=AD=1.
∵∠A=∠ABC=90°,
∴AD∥BC.
∴∠ADB=∠CBD.
∵DB平分∠ADC,∴∠ADB=∠CDB.
∴∠CDB=∠CBD.
∴CB=CD=3.
∵AD=BE=1,∴CE=BC-BE=3-1=2.
在Rt△CDE中,DE=.
∴BD=.
∴sin∠ABD=.
巩固练习
6. (2022·常州)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC. 若AD=1,CD=3,则sin∠ABD的值为________ .
E
B
C
A
D
巩固练习
7. 已知∠A为锐角,且cosA=,求sinA、tanA.
B
A
C
解:如图,∵∠C=90°,cosA==,
∴设AC=5k,AB=13k,由勾股定理,
得BC===12k.
由锐角三角函数定义得,
sinA===,
tanA===.
拓展:
tanA=
巩固练习
8. 证明:锐角三角形的面积等于两边的长与其夹角的正弦值的乘积的一半.
B
C
A
D
解:已知:如图,锐角三角形ABC.
求证:S△ABC=.
证明:过点A作AD⊥BC,垂足为D.
∵sinB=,
∴AD=AB sinB,
∴S△ABC==AB sinB.
考点分析
考点二 特殊角的三角函数值
变式 在△ABC中,两个内角满足|sinA-|+=0,则△ABC的形状是______________.
锐角三角形
例2 在△ABC中,若+=0,则∠C的度数是 ( )
C
A. 45° B. 75° C. 105° D. 120°
巩固练习
1. (2023·天津) sin 45°+的值等于( )
A.1 B. C. D.2
B
2. tan (α+20°)=1,锐角 α 的度数应是 ( )
A. 40° B. 30° C. 20° D. 10°
D
巩固练习
3. (2023·山东)计算: .
1
4. 已知2cosθ=1,则θ= °.
60
5. 已知α是锐角,tanα=2cos30°,则α=______°.
60
解:∵在Rt△BDC中,∠BDC=45°,BD=10,
∴BC=BD·sin∠BDC=10×=10.
∵∠C=90°,AB=20,
∴sinA===,
∴∠A=30°.
∴∠ABD=15°.
巩固练习
6.如图,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠ABD的度数.
A
D
C
B
45°
巩固练习
7.把一根长5cm的铁丝折成顶角为120°的等腰三角形,求此三角形的各边长(精确到0.1cm).
A
C
B
D
解:如图,在△ABC中,∠BAC=120°,
设AB=AC= x,
过点A作AD⊥BC,垂足为D.
则∠BAD=∠CAD=60°,BC=2BD.
∵sin∠BAD=,
∴BD=AB sin∠BAD=AB sin60°,
∴BC=2×AB× sin 60°=,
∵AB+AC+BC=5,
∴2x+=5.
解得x≈1.34cm.
∴AB=AC≈1.34cm,BC≈2.32cm.
例3 若∠A是锐角,且sinA=,则( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
考点三 三角函数的增减性
考点分析
解:∵∠A是锐角,且sinA=<=sin30°,
∴0°<∠A<30°.
A
变式1 已知∠A为锐角,且cosA≤,那么( )
A. B.
C. D.
B
变式2 在Rt△ABC中, ∠C=90°, 当锐角A>30°时, cosA的值的范围为( )
C
A.0<cosA< B.<cosA<1
C.0<cosA< D.<cos A<1
考点分析
巩固练习
1. 当A为锐角,且<cosA<时,∠A的范围是( )
A.30°<∠A<45° B.60°<∠A<90°
C.30°<∠A<60° D.0°<∠A<30°
C
2. 若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
B
巩固练习
3. 红领巾的形状是等腰三角形,底边长为100厘米,腰长为60厘米,则底角( )
A.小于30° B.大于30°且小于45°
C.等于30° D.大于45°且小于60°
A
C
B
D
B
巩固练习
4. (2020·湖南娄底·中考真题)如图,撬钉子的工具是一个杠杆,动力臂,阻力臂,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
A
巩固练习
5. (2023·苏州中学校考一模)化简==_________________.
6.已知tanα=1.237,cosβ=0.9205,sinγ=0.6436(α,β,γ均为锐角),则α,β,γ的大小顺序为__________.(提示:利用函数值的大小与特殊角的函数值的大小关系比较)
β<γ<α
考点分析
考点四 解直角三角形
例4 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
D
30°
45°
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°=,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=4,
∴AB=AD+DB=+4.
变式 如图,在△ABC中,∠B=45°,∠C=30°,BC=1+,求AB及AC的长.
考点分析
C
B
A
D
45°
30°
解:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°.
在Rt△ADB中,∠B=45°,
∴∠BAD=45°.
∴AD=BD,AB=AD.
在Rt△ADC中,∠C=30°,
∴AC=2AD,CD=AD.
设AD=x,则BC=BD+CD=(1+)x,
∴(1+)x=1+,∴x=1.
∴AB=,AC=2.
巩固练习
1. 如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为( )A. B.
C.1 D.2
B
巩固练习
2.(2023·江苏扬州)在中,,,若是锐角三角形,则满足条件的长可以是( )
A.1 B.2 C.6 D.8
C
B
A
D
60°
E
解:如图,作,,交
的延长线于点E
∴,,
∴,,
∵是锐角三角形,
∴,即,
∴满足条件的长可以是6.
C
4
巩固练习
3. 数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B、C、E在同一直线上,若BC=2,求AF的长. 请你运用所学的数学知识解决这个问题.
解:在Rt△ABC中,BC=2,∠A=30°,
∴AC==2,
则EF=AC=2.
∵∠E=45°,
∴FC=EF·sinE=,
∴AF=AC-FC=2-.
巩固练习
4. (2023·江苏连云港)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
解:在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
B
C
D
A
E
O
巩固练习
5. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
巩固练习
6. 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD===5.
当△ABC为锐角三角形时,如图①,
BC=BD+CD=12+5=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
考点五 用锐角三角函数解决问题
考点分析
例5 (2022·江苏南京)如图,灯塔位于港口的北偏东方向,且、之间的距离为,灯塔位于灯塔的正东方向,且、之间的距离为,一艘轮船从港口出发,沿正南方向航行到达处,测得灯塔位于北偏东方向上,这时,处距离港口有多远(结果取整数)?(参考数据:,,,,,)
北
东
B
37°
D
C
58°
A
考点分析
解:过点作的延长线于点
在中,,
∵,,
,
∴,
在中,
∵,,
∴
∴
∴处距离港口约.
H
北
东
B
37°
D
C
58°
A
巩固练习
1.(2023·江苏南通)如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B.
C. D.
B
巩固练习
2.(2023·广东深圳)爬坡时坡角与水平面夹角为,则每爬1m耗能,若某人爬了1000m,该坡角为30°,则他耗能(参考数据:,) ( )
A.58J B.159J C.1025J D.1732J
B
巩固练习
3. (2022·江苏南通) 如图,B为地面上一点,测得B到树底部C的距离为,在B处放置高的测角仪,测得树顶A的仰角为,则树高为__________m(结果保留根号).
解:过点D作交于点E,如图:
则四边形BCED是矩形,
∴BC=DE,BD=CE,
由题意可知:,,
在中,,
∴,
∴.
巩固练习
4.(2022·无锡)如图,某游乐场的大型摩天轮的半径是20m,摩天轮的中心离地面的距离为20.5m,摩天轮旋转1周需要18min.小明乘坐摩天轮从底部点A处出发开始观光,已知点B处离地面的距离为10.5m,小明第一次到达点B处需要 3 min.
3
巩固练习
5.(2023·江苏盐城)如图1,位于市区的“铁军”雕塑“大铜马”是盐城市标志性文化名片,如图2,线段表示“铁军”雕塑的高,点,,在同一条直线上,且,,,则线段的长约为_____m.(计算结果保留整数,参考数据:)
15
巩固练习
6. (2023·江苏连云港) 渔湾是国家“AAAA”级风景区,图1是景区游览的部分示意图.如图2,小卓从九孔桥处出发,沿着坡角为的山坡向上走了到达处的三龙潭瀑布,再沿坡角为的山坡向上走了到达处的二龙潭瀑布.求小卓从处的九孔桥到处的二龙潭瀑布上升的高度为多少米?(结果精确到)
(参考数据:)
巩固练习
E
解:过点作,垂足为.
在中,,
∴
.
过点作,垂足为.
在中,,
∴.
∵,
∴.
答:从处的九孔桥到处的二龙潭瀑布上升的高度约为.
巩固练习
(注:结果精确到,参考数据:,,)
7. (2022·江苏连云港) 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点处测得阿育王塔最高点的仰角,再沿正对阿育王塔方向前进至处测得最高点的仰角,;小亮在点处竖立标杆,小亮的所在位置点、标杆顶、最高点在一条直线上,,.
巩固练习
解:(1)在中,
∵,
∴.
∵,
∴.
在中,由,
得,
解得.
经检验是方程的解
答:阿育王塔的高度约为.
(1)求阿育王塔的高度;
巩固练习
(2)由题意知,
∴,
即,
∴.
经检验是方程的解
答:小亮与阿育王塔之间的距离约为.
(2)求小亮与阿育王塔之间的距离.
巩固练习
8.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.
问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;
解:由于筒车每旋转一周用时120秒,
所以每秒转过360°÷120=3°,
∴∠BOM=360°-3°×95-30°=45°.
巩固练习
(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)
解:如图,分别过点B,A作OM的垂线,垂足为C,D.
在Rt△AOD中,∠AOD=30°,OA=2米,
∴OD=OA=米.
在Rt△BOC中,∠BOC=45°,OB=2米,
∴OC=OB=米,
∴CD=OD-OC=-≈0.3(米).
答:该盛水筒旋转至B处时到水面的距离约为0.3米.
课堂小结
谈谈你本节课的收获是什么?
第7章 锐角三角函数
小结与思考
学习目标
1. 整理本章所学知识,构建本章知识框架;
2. 进一步理解三角函数的概念,明确直角三角形各元素间的关系,进一步学会利用数形结合的思想方法分析问题和解决问题.
知识框架
第7章 锐角三角函数
锐角三角函数
定义
正切:tanA==
正弦:sinA==
余弦:cosA==
A
B
C
斜边c
对边a
邻边b
计算
由定义求锐角三角函数值
由角的度数求锐角三角函数值
由锐角三角函数值求角的度数
一般锐角用计算器
特殊锐角用特殊角的三角函数值
用计算器求一般锐角
根据特殊角的三角函数值求特殊角
互余两角的关系
sinA=cosB=cos(90°-∠A)
cosA=sinB=sin(90°-∠A)
tanA · tanB =1
解直角三角形
知识框架
第7章 锐角三角函数
解直角三角形
定义
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
依据
三边之间的关系:a2+b2=c2 (勾股定理)
锐角之间的关系: ∠A+ ∠B=90°(直角三角形的两个锐角互余)
边、角之间的关系:sinA=,cosA=,tanA=
基本类型
已知一锐角、一边:一锐角、一直角边或一斜边
已知两边:一直角边,一斜边或者两条直角边
简单应用
与仰角、俯角有关的实际问题
与方向角有关的实际问题
与坡角有关的实际问题
与生活有关的其他实际问题
知识回顾
特殊角的锐角三角函数值:
三角函数值 sin θ cos θ tan θ
30°
45°
60°
1
知识回顾
已 知 类 型 已知条件 解 法 步 骤
一边和一锐角 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 斜边和一锐角 (如c,∠A) ①∠B=90°-∠A;
②由sinA=,得a=c·sinA;
③由cosA=,得b=c·cosA
一边和一锐角 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 一直角边和一锐角(如a,∠A) ①∠B=90°-∠A;
②由tanA=,得b=;
③由sinA=,得c=
解直角三角形的基本类型和解法
知识回顾
已 知 类 型 已知条件 解 法 步 骤
两边 (在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边) 斜边和一直角边(如c,a) ①b=;
②由sinA=,求∠A;
③∠B=90°-∠A
两直角边 (a,b) ①c=;
②由tanA=,求∠A;
③∠B=90°-∠A
解直角三角形时,选择关系式的原则:
(1)尽量选可以直接应用原始数据的关系式;
(2)设法选择便于计算的关系式,若能用乘法计算就避免用除法计算.
知识回顾
解直角三角形的简单应用
概念 定义 图形
仰角 俯角
坡度(坡 比)、坡角
方向角
仰角
俯角
视线
水平线
o
视线
铅垂线
当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角.
当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角.
α
l
h
A
B
C
坡面的垂直高度h与水平宽度l的比叫做坡度(坡比),用字母i表示;坡面与水平面的夹角α叫坡角,i=tanα=.
方向角一般是以观测者的位置为中心,将正北(或正南)方向作为起始方向依顺时针(或逆时针)方向到目标方向线之间的锐角.
东
北
O
45°
E
M
25°
60°
N
考点分析
例1 如图,在Rt△ABC中,∠C=90°,BC=6,tanA=. 求AB的长和sinB的值.
B
A
C
6
解:∵在Rt△ABC中,∠C=90°,BC=6,
tanA==,
∴AC=12,
∴AB===6
∴sinB===.
考点一 锐角三角函数的定义
巩固练习
1. 已知等腰三角形的三边长之比为1:1:,则它的顶角为( )
A. 150° B. 120° C. 60° D. 30°
B
2. 在△ABC中,∠C=90°,若sinB+cosA=1,则∠B的度数是( )
A. 60° B. 45° C. 30° D. 不能确定
C
巩固练习
3.(2022·扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边. 若b2=ac,则sin A的值为 .
4.(2023·江苏)如图,在中,,点D在边AB上,连接CD.若,,则______.
B
D
A
C
5. (2022·连云港)如图,在6×6正方形网格中,△ABC的顶点A、B、C都在网格线上,且都是小正方形边的中点,则sinA=_______.
A
B
C
巩固练习
解:过点D作DE⊥BC,垂足为E.易得四边形ABED是矩形,BE=AD=1.
∵∠A=∠ABC=90°,
∴AD∥BC.
∴∠ADB=∠CBD.
∵DB平分∠ADC,∴∠ADB=∠CDB.
∴∠CDB=∠CBD.
∴CB=CD=3.
∵AD=BE=1,∴CE=BC-BE=3-1=2.
在Rt△CDE中,DE=.
∴BD=.
∴sin∠ABD=.
巩固练习
6. (2022·常州)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC. 若AD=1,CD=3,则sin∠ABD的值为________ .
E
B
C
A
D
巩固练习
7. 已知∠A为锐角,且cosA=,求sinA、tanA.
B
A
C
解:如图,∵∠C=90°,cosA==,
∴设AC=5k,AB=13k,由勾股定理,
得BC===12k.
由锐角三角函数定义得,
sinA===,
tanA===.
拓展:
tanA=
巩固练习
8. 证明:锐角三角形的面积等于两边的长与其夹角的正弦值的乘积的一半.
B
C
A
D
解:已知:如图,锐角三角形ABC.
求证:S△ABC=.
证明:过点A作AD⊥BC,垂足为D.
∵sinB=,
∴AD=AB sinB,
∴S△ABC==AB sinB.
考点分析
考点二 特殊角的三角函数值
变式 在△ABC中,两个内角满足|sinA-|+=0,则△ABC的形状是______________.
锐角三角形
例2 在△ABC中,若+=0,则∠C的度数是 ( )
C
A. 45° B. 75° C. 105° D. 120°
巩固练习
1. (2023·天津) sin 45°+的值等于( )
A.1 B. C. D.2
B
2. tan (α+20°)=1,锐角 α 的度数应是 ( )
A. 40° B. 30° C. 20° D. 10°
D
巩固练习
3. (2023·山东)计算: .
1
4. 已知2cosθ=1,则θ= °.
60
5. 已知α是锐角,tanα=2cos30°,则α=______°.
60
解:∵在Rt△BDC中,∠BDC=45°,BD=10,
∴BC=BD·sin∠BDC=10×=10.
∵∠C=90°,AB=20,
∴sinA===,
∴∠A=30°.
∴∠ABD=15°.
巩固练习
6.如图,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠ABD的度数.
A
D
C
B
45°
巩固练习
7.把一根长5cm的铁丝折成顶角为120°的等腰三角形,求此三角形的各边长(精确到0.1cm).
A
C
B
D
解:如图,在△ABC中,∠BAC=120°,
设AB=AC= x,
过点A作AD⊥BC,垂足为D.
则∠BAD=∠CAD=60°,BC=2BD.
∵sin∠BAD=,
∴BD=AB sin∠BAD=AB sin60°,
∴BC=2×AB× sin 60°=,
∵AB+AC+BC=5,
∴2x+=5.
解得x≈1.34cm.
∴AB=AC≈1.34cm,BC≈2.32cm.
例3 若∠A是锐角,且sinA=,则( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
考点三 三角函数的增减性
考点分析
解:∵∠A是锐角,且sinA=<=sin30°,
∴0°<∠A<30°.
A
变式1 已知∠A为锐角,且cosA≤,那么( )
A. B.
C. D.
B
变式2 在Rt△ABC中, ∠C=90°, 当锐角A>30°时, cosA的值的范围为( )
C
A.0<cosA< B.<cosA<1
C.0<cosA< D.<cos A<1
考点分析
巩固练习
1. 当A为锐角,且<cosA<时,∠A的范围是( )
A.30°<∠A<45° B.60°<∠A<90°
C.30°<∠A<60° D.0°<∠A<30°
C
2. 若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
B
巩固练习
3. 红领巾的形状是等腰三角形,底边长为100厘米,腰长为60厘米,则底角( )
A.小于30° B.大于30°且小于45°
C.等于30° D.大于45°且小于60°
A
C
B
D
B
巩固练习
4. (2020·湖南娄底·中考真题)如图,撬钉子的工具是一个杠杆,动力臂,阻力臂,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
A
巩固练习
5. (2023·苏州中学校考一模)化简==_________________.
6.已知tanα=1.237,cosβ=0.9205,sinγ=0.6436(α,β,γ均为锐角),则α,β,γ的大小顺序为__________.(提示:利用函数值的大小与特殊角的函数值的大小关系比较)
β<γ<α
考点分析
考点四 解直角三角形
例4 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
D
30°
45°
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°=,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=4,
∴AB=AD+DB=+4.
变式 如图,在△ABC中,∠B=45°,∠C=30°,BC=1+,求AB及AC的长.
考点分析
C
B
A
D
45°
30°
解:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°.
在Rt△ADB中,∠B=45°,
∴∠BAD=45°.
∴AD=BD,AB=AD.
在Rt△ADC中,∠C=30°,
∴AC=2AD,CD=AD.
设AD=x,则BC=BD+CD=(1+)x,
∴(1+)x=1+,∴x=1.
∴AB=,AC=2.
巩固练习
1. 如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为( )A. B.
C.1 D.2
B
巩固练习
2.(2023·江苏扬州)在中,,,若是锐角三角形,则满足条件的长可以是( )
A.1 B.2 C.6 D.8
C
B
A
D
60°
E
解:如图,作,,交
的延长线于点E
∴,,
∴,,
∵是锐角三角形,
∴,即,
∴满足条件的长可以是6.
C
4
巩固练习
3. 数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B、C、E在同一直线上,若BC=2,求AF的长. 请你运用所学的数学知识解决这个问题.
解:在Rt△ABC中,BC=2,∠A=30°,
∴AC==2,
则EF=AC=2.
∵∠E=45°,
∴FC=EF·sinE=,
∴AF=AC-FC=2-.
巩固练习
4. (2023·江苏连云港)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
解:在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
B
C
D
A
E
O
巩固练习
5. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
巩固练习
6. 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD===5.
当△ABC为锐角三角形时,如图①,
BC=BD+CD=12+5=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
考点五 用锐角三角函数解决问题
考点分析
例5 (2022·江苏南京)如图,灯塔位于港口的北偏东方向,且、之间的距离为,灯塔位于灯塔的正东方向,且、之间的距离为,一艘轮船从港口出发,沿正南方向航行到达处,测得灯塔位于北偏东方向上,这时,处距离港口有多远(结果取整数)?(参考数据:,,,,,)
北
东
B
37°
D
C
58°
A
考点分析
解:过点作的延长线于点
在中,,
∵,,
,
∴,
在中,
∵,,
∴
∴
∴处距离港口约.
H
北
东
B
37°
D
C
58°
A
巩固练习
1.(2023·江苏南通)如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B.
C. D.
B
巩固练习
2.(2023·广东深圳)爬坡时坡角与水平面夹角为,则每爬1m耗能,若某人爬了1000m,该坡角为30°,则他耗能(参考数据:,) ( )
A.58J B.159J C.1025J D.1732J
B
巩固练习
3. (2022·江苏南通) 如图,B为地面上一点,测得B到树底部C的距离为,在B处放置高的测角仪,测得树顶A的仰角为,则树高为__________m(结果保留根号).
解:过点D作交于点E,如图:
则四边形BCED是矩形,
∴BC=DE,BD=CE,
由题意可知:,,
在中,,
∴,
∴.
巩固练习
4.(2022·无锡)如图,某游乐场的大型摩天轮的半径是20m,摩天轮的中心离地面的距离为20.5m,摩天轮旋转1周需要18min.小明乘坐摩天轮从底部点A处出发开始观光,已知点B处离地面的距离为10.5m,小明第一次到达点B处需要 3 min.
3
巩固练习
5.(2023·江苏盐城)如图1,位于市区的“铁军”雕塑“大铜马”是盐城市标志性文化名片,如图2,线段表示“铁军”雕塑的高,点,,在同一条直线上,且,,,则线段的长约为_____m.(计算结果保留整数,参考数据:)
15
巩固练习
6. (2023·江苏连云港) 渔湾是国家“AAAA”级风景区,图1是景区游览的部分示意图.如图2,小卓从九孔桥处出发,沿着坡角为的山坡向上走了到达处的三龙潭瀑布,再沿坡角为的山坡向上走了到达处的二龙潭瀑布.求小卓从处的九孔桥到处的二龙潭瀑布上升的高度为多少米?(结果精确到)
(参考数据:)
巩固练习
E
解:过点作,垂足为.
在中,,
∴
.
过点作,垂足为.
在中,,
∴.
∵,
∴.
答:从处的九孔桥到处的二龙潭瀑布上升的高度约为.
巩固练习
(注:结果精确到,参考数据:,,)
7. (2022·江苏连云港) 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点处测得阿育王塔最高点的仰角,再沿正对阿育王塔方向前进至处测得最高点的仰角,;小亮在点处竖立标杆,小亮的所在位置点、标杆顶、最高点在一条直线上,,.
巩固练习
解:(1)在中,
∵,
∴.
∵,
∴.
在中,由,
得,
解得.
经检验是方程的解
答:阿育王塔的高度约为.
(1)求阿育王塔的高度;
巩固练习
(2)由题意知,
∴,
即,
∴.
经检验是方程的解
答:小亮与阿育王塔之间的距离约为.
(2)求小亮与阿育王塔之间的距离.
巩固练习
8.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.
问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;
解:由于筒车每旋转一周用时120秒,
所以每秒转过360°÷120=3°,
∴∠BOM=360°-3°×95-30°=45°.
巩固练习
(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)
解:如图,分别过点B,A作OM的垂线,垂足为C,D.
在Rt△AOD中,∠AOD=30°,OA=2米,
∴OD=OA=米.
在Rt△BOC中,∠BOC=45°,OB=2米,
∴OC=OB=米,
∴CD=OD-OC=-≈0.3(米).
答:该盛水筒旋转至B处时到水面的距离约为0.3米.
课堂小结
谈谈你本节课的收获是什么?
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
