16.3.1二次根式的加减(同步课件)-2023-2024学年八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 16.3.1二次根式的加减(同步课件)-2023-2024学年八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第16章
二次根式
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
16.3.1
二次根式的加减
情景引入
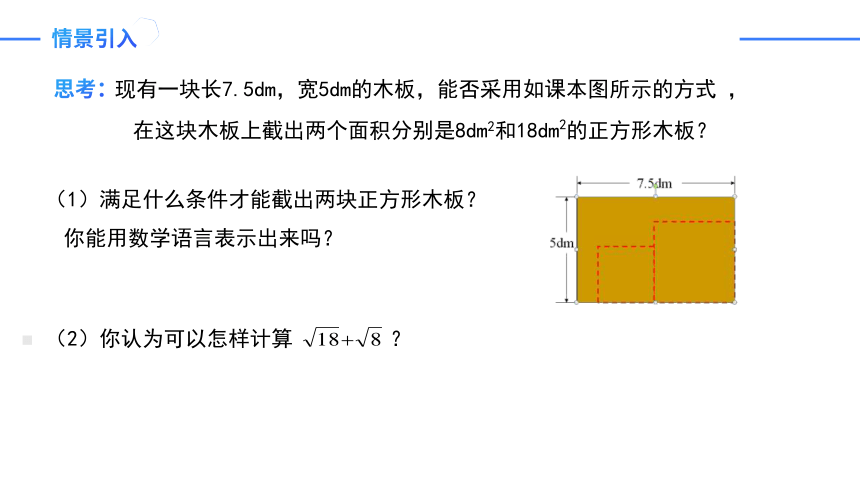
现有一块长7.5dm,宽5dm的木板,能否采用如课本图所示的方式 ,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
(1)满足什么条件才能截出两块正方形木板?你能用数学语言表示出来吗?
(2)你认为可以怎样计算 ?
思考:
复习回顾
(1) 计算结果是多少?说说你的思考过程.
(2) 能合并吗?为什么?
(3) 能合并吗?
如果能合并,说说你的思考过程.
(4) 能直接合并吗?为什么?
思考:
新知探究
思考:
化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
同类二次根式
新知探究
1.定义:
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
2.注意:
判断几个二次根式是否是同类二次根式时:
第一步,将它们化成最简二次根式;
第二步,看它们的被开方数是否相同.
新知探究
思考:
如何将下列二次根式分类?
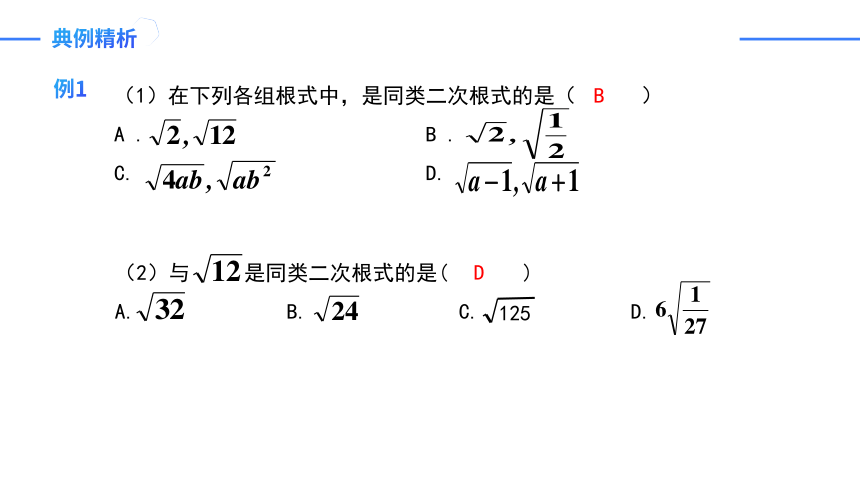
(2)与 是同类二次根式的是( )
A. B. C. D.
典例精析
例1
(1)在下列各组根式中,是同类二次根式的是( )
A . B .
D.
B
125
D
典例精析
例2
解析:首先把选项中每个根式化成最简二次根式,然后
找出被开方数不是3的二次根式.即
下列根式中,不能与 合并的是( )
A. B. C. D.
C
同类二次根式的合并
新知探究
判断两个二次根式是否能合并,应先把二次根式化为最简二次根式,然后判断被开方数是否相同,相同就能合并,否则不能合并.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
典例精析
例3
如果最简二次根式 与 可以合并,求a,b的值.
解:由题意得
解得
典例精析
例4
计算:(1) (2)
解:(1)
(2)
二次根式的加减法法则
新知探究
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,
再将被开方数相同的二次根式进行合并.
化为最简
二次根式
用分配
律合并
整式
加减
依据:二次根式的性质、分配律和整式加减法则.
思想:把二次根式加减问题转化为整式加减问题.
典例精析
例5
解:
计算:
典例精析
加减法的运算步骤
将非最简二次根式的二次根式化简
找出被开方数相同的二次根式;
(1)化
(2)找
(3)合
把被开方数相同的二次根式合并
典例精析
例5
解:
典例精析
将每个二次根式都化为最简二次根式,若被开方数中含有带分数,则要先化成假分数;若含有小数,则要化成分数,进而化为最简二次根式.
化简
合并
原式中若有括号,要先去括号,再应用加法交换律、结合律将被开方数相同的二次根式进行合并.
二次根式加减运算的技巧
典例精析
例6
(1) (2)
(3) (4)
解:(1)原式=
(3)原式=
(2)原式=
(4)原式=
典例精析
易错警示
(1)合并被开方数相同的二次根式时,根号外的因数(式)与因数(式)合并,剩下的部分保持不变,一定不要丢掉;
(2)不能合并的二次根式不能丢掉,因为它们也是结果的一部分;
(3)二次根式根号外的因数是带分数的要化为假分数.
典例精析
例7
有一个等腰三角形的两边长分别为 ,求其周长.
解: 当腰长为 时,
∵
∴此时能构成三角形,周长为
当腰长为 时,
∵
∴此时能构成三角形,周长为
归纳总结
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
当堂检测
1.下列各式化成最简二次根式后被开方数与 的被开方数相同的是( )
A. B. C. D.
2.与- 是同类二次根式的是( )
A. B. C. D.
3.计算3 -2 的结果是( )
A. B.2 C.3 D.6
4.下列计算,正确的是( )
A.(-2)-2=4 B. =-2
C.46÷(-2)6=64 D.
D
C
A
C
当堂检测
5. 与最简二次根式 能合并,则m=_____.
1
6.下列二次根式,不能与 合并的是________(填 序号).
(2)(5)
7.已知一个长方形的长为 ,宽为 ,则其周长为______.
当堂检测
⑴
解:⑴原式=
⑵
8.计算:
(2)原式=
当堂检测
⑶原式=
8.计算:
(3)
(4)
(4)原式=
当堂检测
8.计算:
(5)原式=
(5)
(6)原式=
(6)
当堂检测
9.若最简根式 与 可以合并,求 的值.
解:由题意得 解得
即
当堂检测
10.已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
第16章
二次根式
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
16.3.1
二次根式的加减
情景引入
现有一块长7.5dm,宽5dm的木板,能否采用如课本图所示的方式 ,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
(1)满足什么条件才能截出两块正方形木板?你能用数学语言表示出来吗?
(2)你认为可以怎样计算 ?
思考:
复习回顾
(1) 计算结果是多少?说说你的思考过程.
(2) 能合并吗?为什么?
(3) 能合并吗?
如果能合并,说说你的思考过程.
(4) 能直接合并吗?为什么?
思考:
新知探究
思考:
化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
同类二次根式
新知探究
1.定义:
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
2.注意:
判断几个二次根式是否是同类二次根式时:
第一步,将它们化成最简二次根式;
第二步,看它们的被开方数是否相同.
新知探究
思考:
如何将下列二次根式分类?
(2)与 是同类二次根式的是( )
A. B. C. D.
典例精析
例1
(1)在下列各组根式中,是同类二次根式的是( )
A . B .
D.
B
125
D
典例精析
例2
解析:首先把选项中每个根式化成最简二次根式,然后
找出被开方数不是3的二次根式.即
下列根式中,不能与 合并的是( )
A. B. C. D.
C
同类二次根式的合并
新知探究
判断两个二次根式是否能合并,应先把二次根式化为最简二次根式,然后判断被开方数是否相同,相同就能合并,否则不能合并.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
典例精析
例3
如果最简二次根式 与 可以合并,求a,b的值.
解:由题意得
解得
典例精析
例4
计算:(1) (2)
解:(1)
(2)
二次根式的加减法法则
新知探究
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,
再将被开方数相同的二次根式进行合并.
化为最简
二次根式
用分配
律合并
整式
加减
依据:二次根式的性质、分配律和整式加减法则.
思想:把二次根式加减问题转化为整式加减问题.
典例精析
例5
解:
计算:
典例精析
加减法的运算步骤
将非最简二次根式的二次根式化简
找出被开方数相同的二次根式;
(1)化
(2)找
(3)合
把被开方数相同的二次根式合并
典例精析
例5
解:
典例精析
将每个二次根式都化为最简二次根式,若被开方数中含有带分数,则要先化成假分数;若含有小数,则要化成分数,进而化为最简二次根式.
化简
合并
原式中若有括号,要先去括号,再应用加法交换律、结合律将被开方数相同的二次根式进行合并.
二次根式加减运算的技巧
典例精析
例6
(1) (2)
(3) (4)
解:(1)原式=
(3)原式=
(2)原式=
(4)原式=
典例精析
易错警示
(1)合并被开方数相同的二次根式时,根号外的因数(式)与因数(式)合并,剩下的部分保持不变,一定不要丢掉;
(2)不能合并的二次根式不能丢掉,因为它们也是结果的一部分;
(3)二次根式根号外的因数是带分数的要化为假分数.
典例精析
例7
有一个等腰三角形的两边长分别为 ,求其周长.
解: 当腰长为 时,
∵
∴此时能构成三角形,周长为
当腰长为 时,
∵
∴此时能构成三角形,周长为
归纳总结
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
当堂检测
1.下列各式化成最简二次根式后被开方数与 的被开方数相同的是( )
A. B. C. D.
2.与- 是同类二次根式的是( )
A. B. C. D.
3.计算3 -2 的结果是( )
A. B.2 C.3 D.6
4.下列计算,正确的是( )
A.(-2)-2=4 B. =-2
C.46÷(-2)6=64 D.
D
C
A
C
当堂检测
5. 与最简二次根式 能合并,则m=_____.
1
6.下列二次根式,不能与 合并的是________(填 序号).
(2)(5)
7.已知一个长方形的长为 ,宽为 ,则其周长为______.
当堂检测
⑴
解:⑴原式=
⑵
8.计算:
(2)原式=
当堂检测
⑶原式=
8.计算:
(3)
(4)
(4)原式=
当堂检测
8.计算:
(5)原式=
(5)
(6)原式=
(6)
当堂检测
9.若最简根式 与 可以合并,求 的值.
解:由题意得 解得
即
当堂检测
10.已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
