2023-2024学年人教版七年级数学下册5.2.1平行线练习题(无答案)
文档属性
| 名称 | 2023-2024学年人教版七年级数学下册5.2.1平行线练习题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览

文档简介
第五章 相交线与平行线
5.2.1 平行线
一、单项选择题
1.在同一平面内,不重合的两条直线的位置关系可能是( )
A.平行 B.垂直或平行 C.相交或平行 D.相交或垂直
2.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
3.观察如图所示的长方体,与棱AB平行的棱有几条( )
A. 4 B.3 C.2 D.1
7.过直线l外一点A作l的平行线,可以作( )
A. 1条 B.2条 C.3条 D.4条
8.若直线a∥b,b∥c,则a∥c的依据是( )
A.平行线的基本事实 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
6. 下列说法中正确的个数为( )
①在同一平面内不相交的两条直线叫做平行线;
②平面内经过一点有且只有一条直线与已知直线垂直;
③经过一点有且只有一条直线与已知直线平行;
④平行同一直线的两直线平行.
A.1个 B.2个 C.3个 D.4个
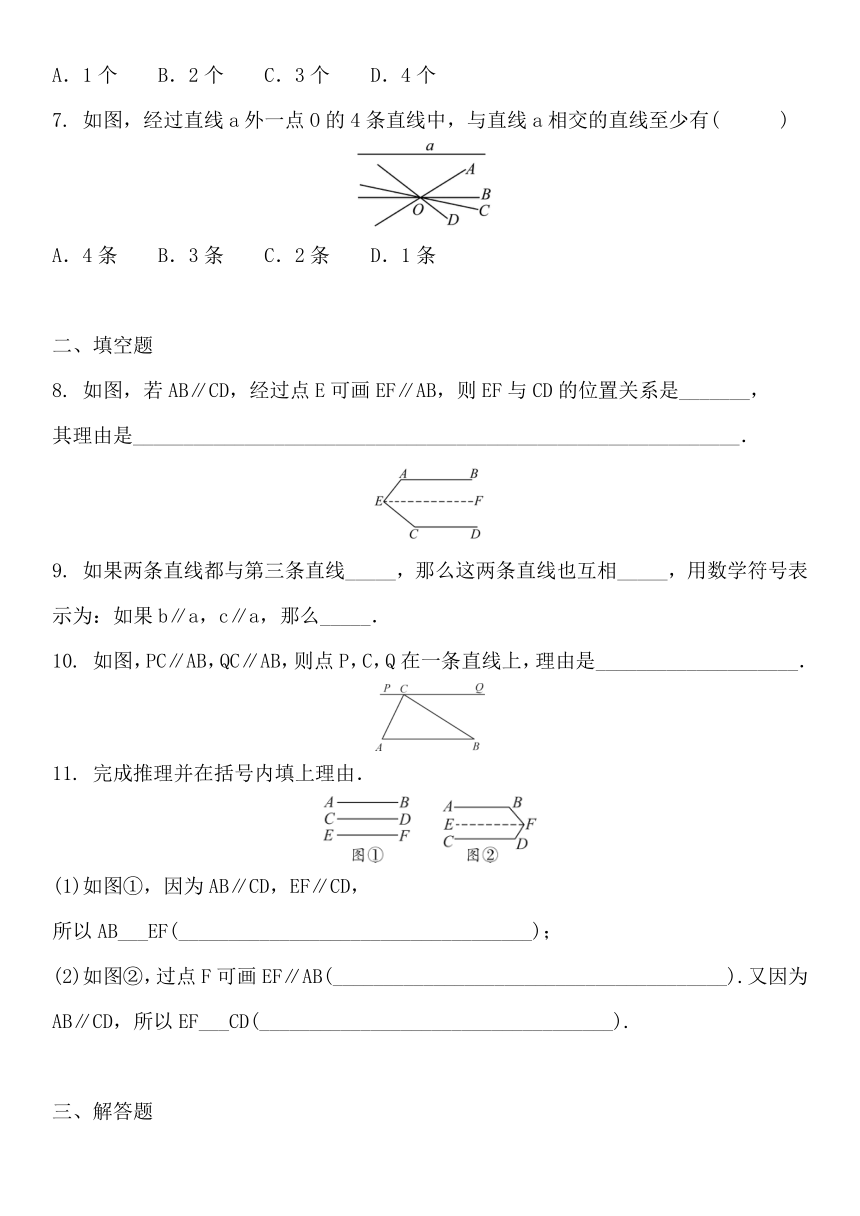
7. 如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
二、填空题
8. 如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的位置关系是_______,
其理由是____________________________________________________________.
9. 如果两条直线都与第三条直线_____,那么这两条直线也互相_____,用数学符号表示为:如果b∥a,c∥a,那么_____.
10. 如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是____________________.
11. 完成推理并在括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB___EF(___________________________________);
(2)如图②,过点F可画EF∥AB(_______________________________________).又因为AB∥CD,所以EF___CD(___________________________________).
三、解答题
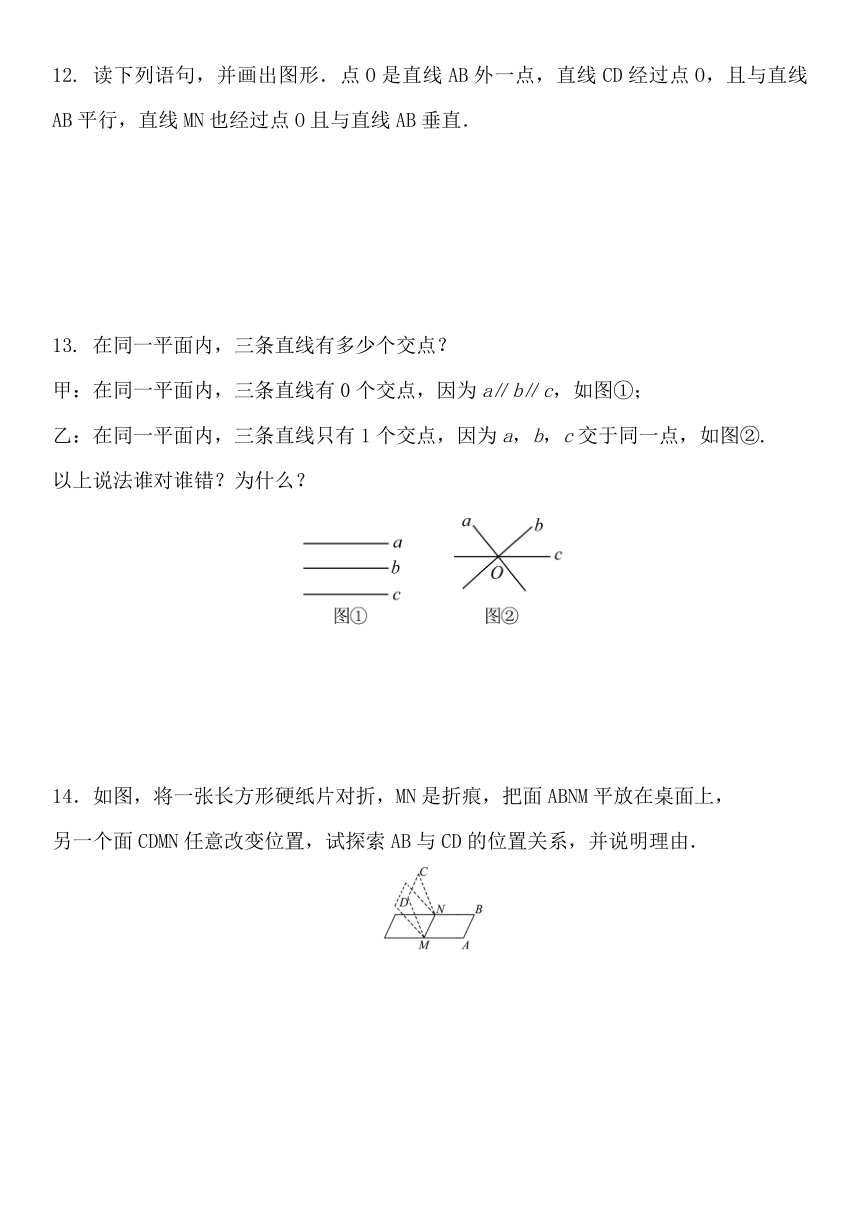
12. 读下列语句,并画出图形.点O是直线AB外一点,直线CD经过点O,且与直线AB平行,直线MN也经过点O且与直线AB垂直.
13. 在同一平面内,三条直线有多少个交点?
甲:在同一平面内,三条直线有0个交点,因为a∥b∥c,如图①;
乙:在同一平面内,三条直线只有1个交点,因为a,b,c交于同一点,如图②.
以上说法谁对谁错?为什么?
14.如图,将一张长方形硬纸片对折,MN是折痕,把面ABNM平放在桌面上,
另一个面CDMN任意改变位置,试探索AB与CD的位置关系,并说明理由.
15. 如图所示,在∠AOB内有一点P.
(1)过点P画l1∥OA;
(2)过点P画l2∥OB;
(3)用量角器量一量l1与l2相交的角与∠O有怎样的大小关系?
16. 如图,P,Q分别是直线EF外两点,画图并回答问题:
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系?为什么?
答案
一、
1-7 CCBAD CB
二、
8. 平行 如果两条直线都与第三条直线平行,那么这两条直线也互相平行
9. 平行 平行 b∥c
10. 经过直线外一点,有且只有一条直线与这条直线平行
11. (1) ∥ 平行于同一条直线的两条直线互相平行
(2) 过直线外一点可画一条直线与已知直线平行
∥ 平行于同一条直线的两条直线互相平行
三、
12. 解:如图所示:
13. 解:都不对,因为除了甲、乙两种说法外,在同一平面内,三条直线交点的个数还有两种情况,即有2个交点或3个交点,如图:
所以在同一平面内,三条直线有0个或1个或2个或3个交点
14. 解:AB∥CD.理由:因为MN为长方形纸片对折折痕,所以MN∥AB,MN∥CD,
所以AB∥CD,即如果两条直线都与第三条直线平行,那么这两条直线也互相平行
15. 解:(1)(2)如图所示
(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补
16. 解:(1)图略
(2)AB∥CD.理由:因为AB∥EF,CD∥EF,所以AB∥CD,即如果两条直线都与第三条直线平行,那么这两条直线也互相平行
5.2.1 平行线
一、单项选择题
1.在同一平面内,不重合的两条直线的位置关系可能是( )
A.平行 B.垂直或平行 C.相交或平行 D.相交或垂直
2.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
3.观察如图所示的长方体,与棱AB平行的棱有几条( )
A. 4 B.3 C.2 D.1
7.过直线l外一点A作l的平行线,可以作( )
A. 1条 B.2条 C.3条 D.4条
8.若直线a∥b,b∥c,则a∥c的依据是( )
A.平行线的基本事实 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
6. 下列说法中正确的个数为( )
①在同一平面内不相交的两条直线叫做平行线;
②平面内经过一点有且只有一条直线与已知直线垂直;
③经过一点有且只有一条直线与已知直线平行;
④平行同一直线的两直线平行.
A.1个 B.2个 C.3个 D.4个
7. 如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
二、填空题
8. 如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的位置关系是_______,
其理由是____________________________________________________________.
9. 如果两条直线都与第三条直线_____,那么这两条直线也互相_____,用数学符号表示为:如果b∥a,c∥a,那么_____.
10. 如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是____________________.
11. 完成推理并在括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB___EF(___________________________________);
(2)如图②,过点F可画EF∥AB(_______________________________________).又因为AB∥CD,所以EF___CD(___________________________________).
三、解答题
12. 读下列语句,并画出图形.点O是直线AB外一点,直线CD经过点O,且与直线AB平行,直线MN也经过点O且与直线AB垂直.
13. 在同一平面内,三条直线有多少个交点?
甲:在同一平面内,三条直线有0个交点,因为a∥b∥c,如图①;
乙:在同一平面内,三条直线只有1个交点,因为a,b,c交于同一点,如图②.
以上说法谁对谁错?为什么?
14.如图,将一张长方形硬纸片对折,MN是折痕,把面ABNM平放在桌面上,
另一个面CDMN任意改变位置,试探索AB与CD的位置关系,并说明理由.
15. 如图所示,在∠AOB内有一点P.
(1)过点P画l1∥OA;
(2)过点P画l2∥OB;
(3)用量角器量一量l1与l2相交的角与∠O有怎样的大小关系?
16. 如图,P,Q分别是直线EF外两点,画图并回答问题:
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系?为什么?
答案
一、
1-7 CCBAD CB
二、
8. 平行 如果两条直线都与第三条直线平行,那么这两条直线也互相平行
9. 平行 平行 b∥c
10. 经过直线外一点,有且只有一条直线与这条直线平行
11. (1) ∥ 平行于同一条直线的两条直线互相平行
(2) 过直线外一点可画一条直线与已知直线平行
∥ 平行于同一条直线的两条直线互相平行
三、
12. 解:如图所示:
13. 解:都不对,因为除了甲、乙两种说法外,在同一平面内,三条直线交点的个数还有两种情况,即有2个交点或3个交点,如图:
所以在同一平面内,三条直线有0个或1个或2个或3个交点
14. 解:AB∥CD.理由:因为MN为长方形纸片对折折痕,所以MN∥AB,MN∥CD,
所以AB∥CD,即如果两条直线都与第三条直线平行,那么这两条直线也互相平行
15. 解:(1)(2)如图所示
(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补
16. 解:(1)图略
(2)AB∥CD.理由:因为AB∥EF,CD∥EF,所以AB∥CD,即如果两条直线都与第三条直线平行,那么这两条直线也互相平行
