第一单元圆柱与圆锥常考专项检测卷-数学六年级下册北师大版(含答案)
文档属性
| 名称 | 第一单元圆柱与圆锥常考专项检测卷-数学六年级下册北师大版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 482.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
第一单元圆柱与圆锥常考易错检测卷-数学六年级下册北师大版
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、选择题(共18分)
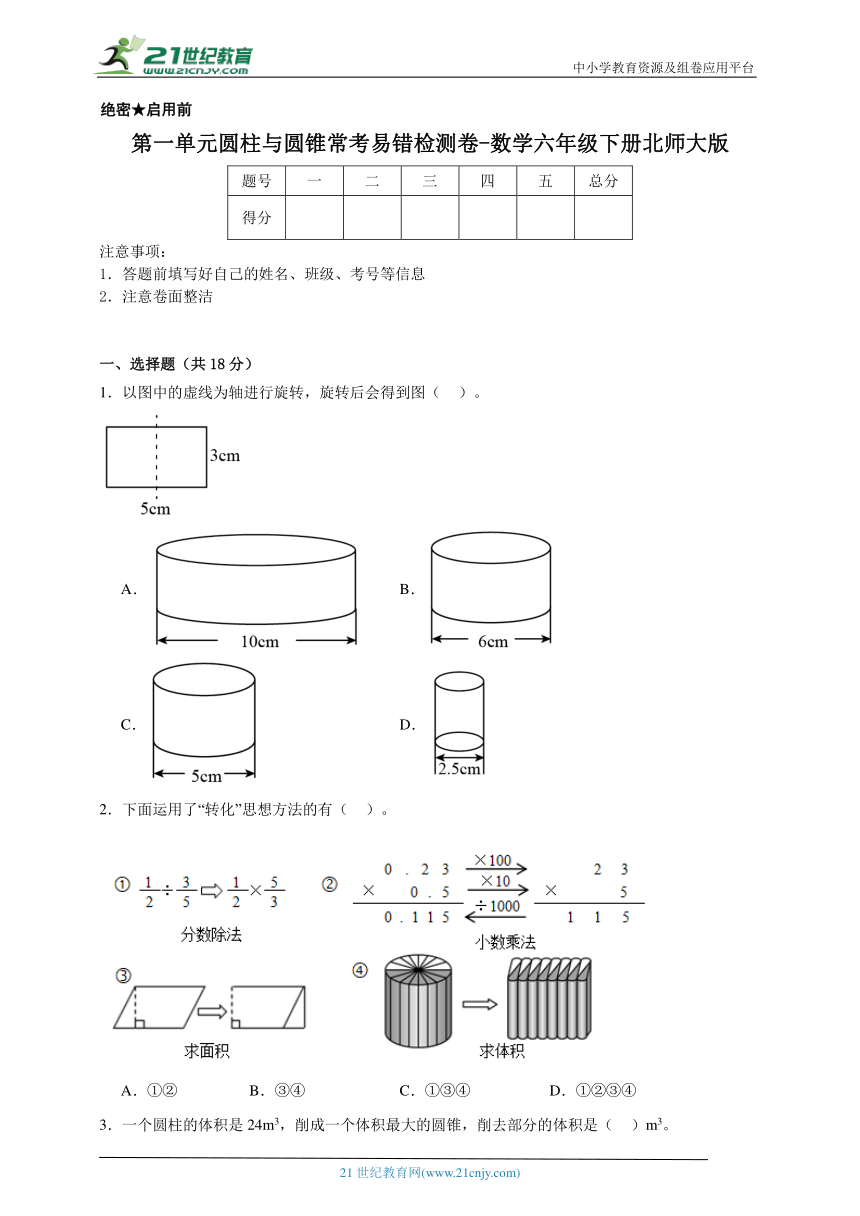
1.以图中的虚线为轴进行旋转,旋转后会得到图( )。
A. B.
C. D.
2.下面运用了“转化”思想方法的有( )。
A.①② B.③④ C.①③④ D.①②③④
3.一个圆柱的体积是24m3,削成一个体积最大的圆锥,削去部分的体积是( )m3。
A.24 B.16 C.8 D.6
4.一个高是9cm,底面积是12.56cm2的圆锥,它的体积是( )cm3。
A.37.68 B.113.04 C.75.36 D.56.52
5.一个圆柱和一个圆锥,它们的体积相等,高都是10厘米。如果圆柱的底面积是36平方厘米,那么圆锥的底面积是( )平方厘米。
A.36 B.12 C.108 D.24
6.一根圆柱形输油管,内直径是4dm,油在管内的流速是4 dm/s,每秒流过的油是( )cm3。
A.50240 B.2512 C.628 D.12560
二、填空题(每空2分,共16分)
7.如图所示,将一个高10厘米、底面半径3厘米的圆柱平均分成32份,拼成一个近似的长方体,它的体积是( )立方厘米,表面积比原来增加了( )平方厘米。
8.把一个圆柱切开拼成一个近似的长方体,拼成后的长方体的表面积比圆柱的表面积增加,已知圆柱高是20cm,圆柱体积是( )。
9.一个圆柱体的侧面积是942平方厘米,体积是2355立方厘米,它的底面半径是( )。
10.高相等,底面半径之比是1∶2的圆柱与圆锥,它们的体积之比是( )∶( )。
11.与一个圆锥等底等高的圆柱的体积是30立方米,圆锥的体积是( )立方米。
12.把一根2m长的圆柱形木料截成相等的3段后,表面积比原来增加了60cm2,原来圆柱形木料的体积是( )cm3。
三、判断题(共10分)
13.一个圆柱的侧面展开图是正方形,说明圆柱的底面周长和高相等。( )
14.用一张长方形纸能围成不同的两个圆柱,它们的体积相等。( )
15.一段长是12dm底面半径是3dm的圆柱形木料,把它锯成长短不同三小段圆柱形木料,表面积比原来增加了113.04dm2。( )
16.一个圆柱形橡皮泥的高是7厘米,把它捏成底面半径相同的圆锥,这个圆锥的高是21厘米。( )
17.一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥大。圆柱的体积是。( )
四、计算题(共20分)
18.计算下面半个圆柱的表面积。(每题5分,共5分)
19.计算下图的体积。(每题5分,共5分)
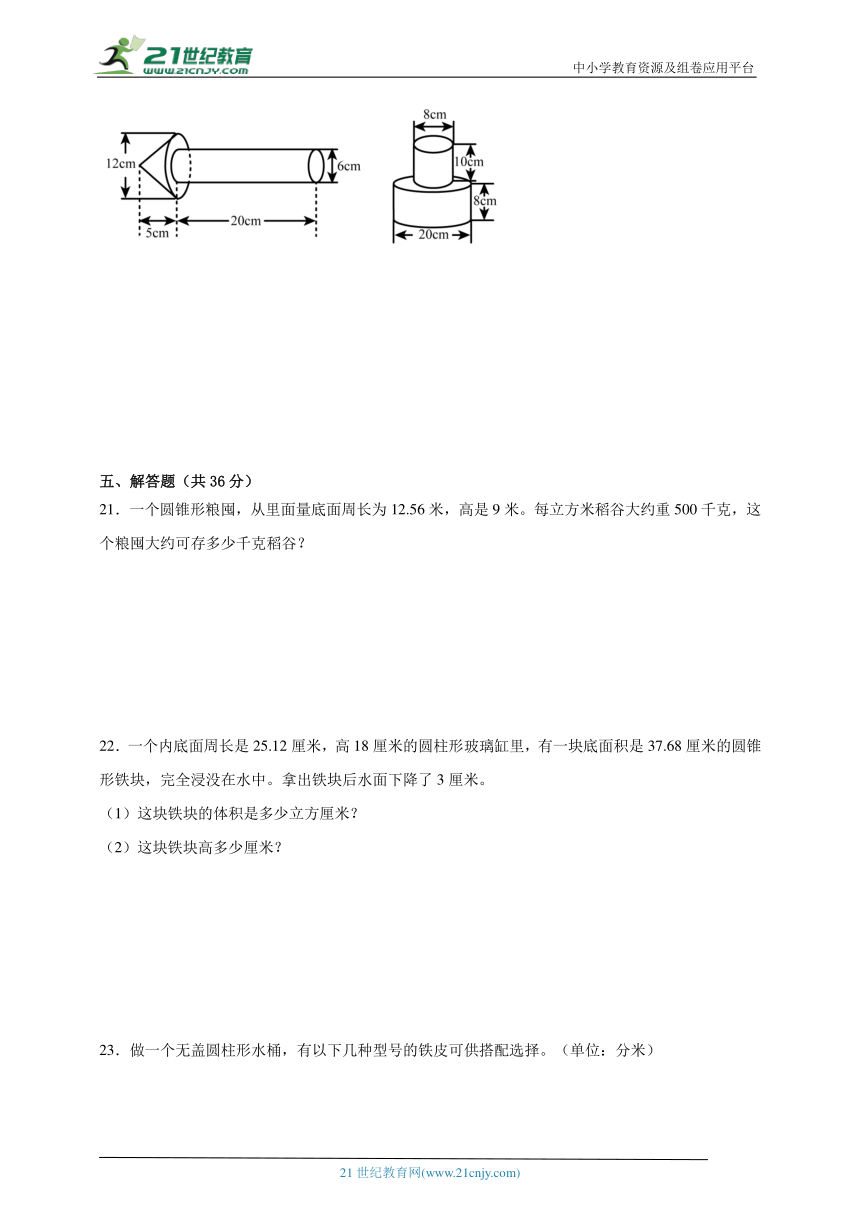
20.计算下左图中图形的体积与下右图中图形的表面积。(每题5分,共10分)
五、解答题(共36分)
21.一个圆锥形粮囤,从里面量底面周长为12.56米,高是9米。每立方米稻谷大约重500千克,这个粮囤大约可存多少千克稻谷?
22.一个内底面周长是25.12厘米,高18厘米的圆柱形玻璃缸里,有一块底面积是37.68厘米的圆锥形铁块,完全浸没在水中。拿出铁块后水面下降了3厘米。
(1)这块铁块的体积是多少立方厘米?
(2)这块铁块高多少厘米?
23.做一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。(单位:分米)
(1)你选择的是( )和( )搭配使用。(填序号)
(2)你选择的材料制成水桶需要铁皮多少平方分米?
(3)你选择的材料制成的水桶最多能装水多少升?(铁皮的厚度略去不计)
24.一根圆柱形木材长2米,把它截成相等的4段后,表面积增加了18.84平方分米。原来这根圆木的体积是多少立方分米?
25.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
26.一个圆柱形容器,从里面量得底面直径是10厘米,此时水面高12厘米,将一底面直径比圆柱底面直径少的圆锥形钢材放入,待完全浸没在水中后,水面上升到13厘米(水没有溢出),圆锥形钢材的高是多少厘米?
参考答案:
1.C
【分析】以图中的虚线为轴进行旋转得到一个圆柱体,此时长方形的宽为圆柱的高,长方形的长为圆柱的底面直径;据此解答
【详解】根据圆柱的特征可知:以图中的虚线为轴进行旋转得到的是一个底面直径为5cm高为3cm的圆柱。
故答案为:C
【点睛】本题主要考查圆柱的特征,解题时注意旋转时不是以长方形的宽为轴进行旋转的。
2.D
【分析】转化是数学的一种思想方法,是把新知识转化为学过的旧知识解决新问题的方法,根据分数除法的计算方法、圆周长公式的推导过程、圆面积公式的推导过程逐个进行分析得出结论。
【详解】①一个数除以分数:一个数除以分数,等于这个数乘分数的倒数,再利用分数乘法的计算法则计算,利用了转化思想;
②计算小数乘法,根据小数的基本性质,先把小数化成整数,运用了转化的思想;
③探索平行四边形的面积时,利用割补法,将平行四边形剪切成长方形,运用了转化的思想;
④求圆柱的体积,利用割补法,将圆柱沿着底面半径和高切拼成小长方体,运用了转化的思想。
①②③④都运用了转化的思想。
故答案为:D
【点睛】本题是考查分数除法、小数乘法的计算方法,平行四边形面积公式的推导,圆柱的体积公式的推导,关键是利用“转化”思想解决问题。
3.B
【分析】等底等高的圆锥的体积是圆柱体积的。把圆柱削成一个体积最大的圆锥,那么圆锥和圆柱为等底等高,则圆锥的体积是圆柱体积的,那么削去部分的体积是圆柱体积的,据此即可算出削去部分的体积。
【详解】由分析可知:24×(1-)
=24×
=16(m )
削去部分的体积是16m 。
故答案为:B
【点睛】此题考查等底等高的圆柱与圆锥的体积关系,要求学生能根据它们之间的数量关系解决实际问题。
4.A
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】12.56×9×
=113.04×
=37.68(cm3)
一个高是9cm,底面积是12.56cm2的圆锥,它的体积是37.68cm3。
故答案为:A
【点睛】熟练掌握圆锥的体积公式是解答本题的关键。
5.C
【分析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高也相等时,圆锥的底面积是圆柱底面积的3倍;据此解答。
【详解】36×3=108(平方厘米)
圆锥的底面积是108平方厘米。
故答案为:C
【点睛】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用。
6.A
【分析】已知一根圆柱形输油管,内直径是4dm(40cm),油在输油管内的形状是圆柱形,油在管内的流速是4 dm/s(40cm/s),相当于圆柱的高;由此可利用圆柱的体积公式V=sh求出每秒流油的体积;据此解答。
【详解】4dm=40cm,4 dm/s=40cm/s,
3.14×(40÷2)2×40
=3.14×400×40
=1256×40
=50240(cm3)
每秒流过的油是50240 cm3。
故答案为:A
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
7. 90π 60
【分析】根据圆柱的体积公式即可求出长方体的体积,表面积比原来增加了两个长方形的面积。
【详解】体积为:
π×32×10
=π×9×10
=90π(立方厘米)
表面积比原来增加了:
10×3×2
=30×2
=60(平方厘米)
它的体积是90π立方厘米,表面积比原来增加了60平方厘米。
【点睛】本题考查了认识立体图形,熟练掌握圆柱的体积公式和长方体的表面积公式是关键。
8.6.28
【分析】把圆柱拼成一个近视长方体,表面积就是增加了两个长是圆柱的高,宽是圆柱底面半径的两个长方形的面积,根据长方形面积公式:面积=长×宽,宽=面积÷长,求出圆柱底面半径,再根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【详解】400÷2÷20
=200÷20
=10(cm)
3.14×102×20
=3.14×100×20
=314×20
=6280(cm3)
6280cm3=6.28dm3
把一个圆柱切开拼成一个近似的长方体,拼成后的长方体的表面积比圆柱的表面积增加400cm3,已知圆柱高是20cm,圆柱体积是6.28dm3。
【点睛】解答本题的关键明确表面积增加了两个长是圆柱的高,宽是圆柱的半径的长方形的面积,注意单位名数的换算。
9.5厘米
【详解】略
10. 3 4
【分析】结合题意,把圆柱的底面半径看作1,则圆锥的底面半径就是2,设它们的高都为h;分别求出圆锥、圆柱的体积,即可求得它们的体积比。
【详解】设圆柱的底面半径为1,则圆锥的底面半径为2,它们的高相等,记为h,则圆锥的体积=×22×πh=πh,圆柱的体积=πh;
πh∶πh
=(πh÷πh)∶(πh÷πh)
=1∶
=3∶4
高相等,底面半径之比是1∶2的圆柱与圆锥,它们的体积之比是3∶4。
【点睛】此题考查了圆锥和圆柱的体积公式的实际应用。
11.10
【分析】等底等高的圆锥的体积是圆柱的体积的倍,由此即可求出圆锥的体积解决问题。
【详解】30×=10(立方米)
圆锥体积是10立方米。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
12.3000
【分析】根据题意可知,把这个圆柱截成3段,需要截2次,每截一次就增加两个截面,由此可知,表面积增加的是4个截面的面积,据此可以求出圆柱的底面积,然后根据圆柱的体积公:V=Sh,把数据代入公式解答。
【详解】2米=200厘米
60÷4×200
=15×200
=3000(cm3)
原来圆柱形木料的体积是3000cm3。
【点睛】此题主要考查圆柱的表面积公式、体积公式的灵活用,关键是熟记公式。
13.√
【分析】根据圆柱体的特征,它的上下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形或正方形,长方形的长等于圆柱体的底面周长,宽等于圆柱体的高;由此解答。
【详解】根据圆柱体的侧面展开图的长、宽与圆柱体的底面周长和高的关系,如果圆柱的侧面展开后是一个正方形,那么这个圆柱的高和底面周长一定相等。原题的说法正确。
故答案为:√
【点睛】此题主要考查圆柱的特征,以及侧面展开图的长、宽与圆柱体的底面周长和高的关系。
14.×
【分析】根据圆柱的体积公式:体积=底面积×高;用一张长方形纸围成不同的两个圆柱,如果长等于宽,则围成的两个圆柱的体积相等;如果长和宽不相等,两个圆柱的底面半径不同,高也不同,所以它们的体积不相等,据此解答。
【详解】根据分析可知,用一张长方形纸能围成不同的两个圆柱,它们的体积不一定相等。
原题干说法错误。
故答案为:×
【点睛】根据长方形的特征以及圆柱的体积公式进行解答。
15.√
【分析】把圆柱形木料锯成长短不同的三小段圆柱形木料,增加4个底面圆的面积。根据圆的面积公式:面积=π×半径2,代入数据,求出一个底面圆的面积,再乘4,再进行比较,即可解答。
【详解】3.14×32×4
=3.14×9×4
=28.26×4
=113.04(dm2)
一段长是12dm底面半径是3dm的圆柱形木料,把它锯成长短不同三小段圆柱形木料,表面积比原来增加了113.04dm2。
原题干说法正确。
故答案为:√
【点睛】圆柱每锯一次,会增加两个圆的面积。如果沿圆柱的底面直径切割,会增加两个长方形的面积。
16.√
【分析】根据圆柱体积公式:V=Sh,圆锥体积公式:V=Sh,若把圆锥体积看作单位“1”,则同底等高的圆柱体积是该圆锥体积的3倍,所以当圆柱和圆锥的体积相等、底面积也相等时,圆锥的高就是圆柱高的3倍,据此解答即可。
【详解】由分析可得:
同底等高时,圆柱高是7厘米,
则圆锥高为:7×3=21(厘米)
综上所述:一个圆柱形橡皮泥的高是7厘米,把它捏成底面半径相同的圆锥,这个圆锥的高是21厘米。
故答案为:√
【点睛】本题考查了同底等高的圆柱和圆锥体积之间的关系,熟记圆柱和圆锥的体积公式是解题的关键。
17.√
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,用体积差除以倍数差,即可求出一倍数,即圆锥体积。再用圆锥体积×3=圆柱体积,据此解题即可。
【详解】圆锥体积为:
24÷(3-1)
=24÷2
=12(dm3)
圆柱体积为:
12×3=36(dm3)
故答案为:√
【点睛】此题解题的关键是理解等底等高的圆柱和圆锥体积之间的关系。
18.151.62dm2
【分析】由图可知:这个半圆柱的表面积包括一个长方形的面积,圆柱的侧面积的一半及上下两个半圆的面积之和就是一个底面积;根据圆柱的表面积公式:,其中,,,代入数据进行计算即可。
【详解】
19.94.2cm3
【分析】本题可以看作是求一个底面直径为6cm,高为(4+6)cm的圆锥的体积,圆锥的体积公式:V=πr2h,把数据代入公式求出即可。
【详解】×3.14×(6÷2)2×(4+6)
=3.14×3×10
=94.2(cm3)
20.753.6立方厘米;1381.6平方厘米
【分析】根据作图可知,是由一个圆柱和一个圆锥组成,根据圆柱的体积公式:底面积×高,圆锥的体积同时:底面积×高÷3,把数代入即可求解;
第二个图的表面积:相当于下面一个圆柱的表面积加上上面圆柱的侧面积,根据圆柱的侧面积公式:底面周长×高,圆柱的底面面积:S=πr2,把数代入公式,把两个圆柱的侧面积相加,再加两个下面圆柱的底面积即可求解。
【详解】第一个:
3.14×(6÷2)2×20+3.14×(12÷2)2×5÷3
=3.14×9×20+3.14×36×5÷3
=565.2+188.4
=753.6(立方厘米)
第二个:
3.14×(20÷2)2×2+3.14×20×8+3.14×8×10
=3.14×100×2+3.14×160+3.14×80
=628+502.4+251.2
=1381.6(平方厘米)
21.18840千克
【分析】要求这个粮囤能装稻谷的重量,先求得粮囤的体积,粮囤的形状是圆锥形的,利用圆锥的体积公式:求得体积,再进一步求得稻谷的重量。问题得解。
【详解】12.56÷3.14÷2
=4÷2
=2(米)
2×2×3.14××9×500
=12.56×3×500
=37.68×500
=18840(千克)
答:这个粮囤大约可存18840千克稻谷。
【点睛】此题主要考查学生对圆锥的体积计算公式掌握与运用情况。
22.(1)150.72立方厘米
(2)12cm
【分析】分析条件后可得出“铁块的体积=水面下降后减少的水那一部分的体积”,则求这块铁块的体积是多少,也就是求周长是25.12厘米,高是3厘米的圆柱形容器里水的体积,先求出此圆柱的半径,再根据圆柱的体积公式V=πr2h解答即可;要求圆锥的高根据圆锥的体积公式:V=πr2h,那么h=V÷÷πr2,把数据代入公式解答。
【详解】(1)25.12÷3.14÷2
=8÷2
=4(cm)
42×3.14×3
=16×3.14×3
=50.24×3
=150.72(cm3)
答:这块铁块的体积是150.72立方厘米。
(2)150.72×3÷37.68
=452.16÷37.68
=12(cm)
答:这块铁块高12厘米。
【点睛】本题主要考查不规则物体体积的求法,关键明确求这块铁块的体积,也就是求底面周长是25.12厘米的圆柱的半径,再求出高是3厘米的圆柱形容器里水的体积。
23.(1)②③;
(2)75.36平方分米;
(3)62.8升
【分析】(1)要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长,与之相配的是②号和③号;
(2)由于水桶无盖,使用只求这个圆柱的一个底面和侧面的总面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=ch,把数据代入公式解答;
(3)求水桶的容积就是求底面周长是12.56分米,高是5分米的圆柱的体积。
【详解】(1)要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长,
2号周长是:3.14×4=12.56(分米)
4号周长是:
2×3.14×3
=6.28×3
=18.84(分米)
所以相配的是②号和③号。
(2)3.14×(4÷2)2+3.14×4×5
=3.14×4+12.56×5
=12.56+62.8
=75.36(平方分米)
答:你选择的材料制成水桶需要铁皮75.36平方分米。
(3)3.14×(4÷2)2×5
=3.14×4×5
=3.14×20
=62.8(立方分米)
=62.8(升)
答:你选择的材料制成的水桶最多能装水62.8升。
【点睛】本题主要考查了圆柱的体积公式V=Sh=πr2h在实际生活中的应用。
24.62.8立方分米
【分析】截成相等的4段后,表面积增加(4-1)×2=6个底面面积,总增加的面积÷底面个数求出木材底面面积,再代入体积公式:V=Sh计算即可。
【详解】2米=20分米
(4-1)×2
=3×2
=6(个)
18.84÷6×20
=3.14×20
=62.8(立方分米)
答:原来这根圆木的体积是62.8立方分米。
【点睛】本题主要考查圆柱的体积公式,明确截成4段后,增加6个底面面积是解题的关键。
25.0.5厘米
【分析】把圆锥的底面半径看作单位“1”,高比底面直径少,也就是高相当于底面直径的(1-),根据一个数乘分数的意义,用乘法求出圆锥的高,再根据圆锥的体积公式: 求出圆锥铁块的体积,然后根据圆柱的体积公式:,用圆锥铁块的体积除以圆柱形容器的底面积就是水面上升的高度。
【详解】圆锥体铁块的高:
5×2×(1-)
=10×
=6(厘米)
圆锥体铁块的体积:
=
=
=157(立方厘米)
圆柱的底面积:
=
=314(平方厘米)
157÷314=0.5(厘米)
答:铁块放入后水面会上升0.5厘米。
【点睛】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
26.厘米
【分析】由于圆锥的底面直径比圆柱底面直径少,则圆锥的底面直径相当于圆柱的:1-,单位“1”已知,用乘法,即10×(1-)=6(厘米)。由于物体完全浸没在水中,水面上升到13厘米,根据公式:容器的底面积×水面变化的高度=物体的体积,即用圆柱的底面积×(13-12),求出圆锥的体积,再根据圆锥的体积公式:底面积×高×,把数代入公式即可求出圆锥形钢材的高。
【详解】10×(1-)
=10×
=6(厘米)
6÷2=3(厘米)
10÷2=5(厘米)
3.14×5×5×(13-12)
=78.5×1
=78.5(立方厘米)
78.5×3÷(3.14×3×3)
=78.5×3÷3.14÷3÷3
=78.5÷3.14÷3
=25÷3
=(厘米)
答:圆锥形钢材的高是厘米。
【点睛】本题主要考查圆柱和圆锥的体积公式,熟练掌握它们的体积公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
第一单元圆柱与圆锥常考易错检测卷-数学六年级下册北师大版
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、选择题(共18分)
1.以图中的虚线为轴进行旋转,旋转后会得到图( )。
A. B.
C. D.
2.下面运用了“转化”思想方法的有( )。
A.①② B.③④ C.①③④ D.①②③④
3.一个圆柱的体积是24m3,削成一个体积最大的圆锥,削去部分的体积是( )m3。
A.24 B.16 C.8 D.6
4.一个高是9cm,底面积是12.56cm2的圆锥,它的体积是( )cm3。
A.37.68 B.113.04 C.75.36 D.56.52
5.一个圆柱和一个圆锥,它们的体积相等,高都是10厘米。如果圆柱的底面积是36平方厘米,那么圆锥的底面积是( )平方厘米。
A.36 B.12 C.108 D.24
6.一根圆柱形输油管,内直径是4dm,油在管内的流速是4 dm/s,每秒流过的油是( )cm3。
A.50240 B.2512 C.628 D.12560
二、填空题(每空2分,共16分)
7.如图所示,将一个高10厘米、底面半径3厘米的圆柱平均分成32份,拼成一个近似的长方体,它的体积是( )立方厘米,表面积比原来增加了( )平方厘米。
8.把一个圆柱切开拼成一个近似的长方体,拼成后的长方体的表面积比圆柱的表面积增加,已知圆柱高是20cm,圆柱体积是( )。
9.一个圆柱体的侧面积是942平方厘米,体积是2355立方厘米,它的底面半径是( )。
10.高相等,底面半径之比是1∶2的圆柱与圆锥,它们的体积之比是( )∶( )。
11.与一个圆锥等底等高的圆柱的体积是30立方米,圆锥的体积是( )立方米。
12.把一根2m长的圆柱形木料截成相等的3段后,表面积比原来增加了60cm2,原来圆柱形木料的体积是( )cm3。
三、判断题(共10分)
13.一个圆柱的侧面展开图是正方形,说明圆柱的底面周长和高相等。( )
14.用一张长方形纸能围成不同的两个圆柱,它们的体积相等。( )
15.一段长是12dm底面半径是3dm的圆柱形木料,把它锯成长短不同三小段圆柱形木料,表面积比原来增加了113.04dm2。( )
16.一个圆柱形橡皮泥的高是7厘米,把它捏成底面半径相同的圆锥,这个圆锥的高是21厘米。( )
17.一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥大。圆柱的体积是。( )
四、计算题(共20分)
18.计算下面半个圆柱的表面积。(每题5分,共5分)
19.计算下图的体积。(每题5分,共5分)
20.计算下左图中图形的体积与下右图中图形的表面积。(每题5分,共10分)
五、解答题(共36分)
21.一个圆锥形粮囤,从里面量底面周长为12.56米,高是9米。每立方米稻谷大约重500千克,这个粮囤大约可存多少千克稻谷?
22.一个内底面周长是25.12厘米,高18厘米的圆柱形玻璃缸里,有一块底面积是37.68厘米的圆锥形铁块,完全浸没在水中。拿出铁块后水面下降了3厘米。
(1)这块铁块的体积是多少立方厘米?
(2)这块铁块高多少厘米?
23.做一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。(单位:分米)
(1)你选择的是( )和( )搭配使用。(填序号)
(2)你选择的材料制成水桶需要铁皮多少平方分米?
(3)你选择的材料制成的水桶最多能装水多少升?(铁皮的厚度略去不计)
24.一根圆柱形木材长2米,把它截成相等的4段后,表面积增加了18.84平方分米。原来这根圆木的体积是多少立方分米?
25.一个圆锥体铁块,底面半径是5厘米,高比底面直径少,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
26.一个圆柱形容器,从里面量得底面直径是10厘米,此时水面高12厘米,将一底面直径比圆柱底面直径少的圆锥形钢材放入,待完全浸没在水中后,水面上升到13厘米(水没有溢出),圆锥形钢材的高是多少厘米?
参考答案:
1.C
【分析】以图中的虚线为轴进行旋转得到一个圆柱体,此时长方形的宽为圆柱的高,长方形的长为圆柱的底面直径;据此解答
【详解】根据圆柱的特征可知:以图中的虚线为轴进行旋转得到的是一个底面直径为5cm高为3cm的圆柱。
故答案为:C
【点睛】本题主要考查圆柱的特征,解题时注意旋转时不是以长方形的宽为轴进行旋转的。
2.D
【分析】转化是数学的一种思想方法,是把新知识转化为学过的旧知识解决新问题的方法,根据分数除法的计算方法、圆周长公式的推导过程、圆面积公式的推导过程逐个进行分析得出结论。
【详解】①一个数除以分数:一个数除以分数,等于这个数乘分数的倒数,再利用分数乘法的计算法则计算,利用了转化思想;
②计算小数乘法,根据小数的基本性质,先把小数化成整数,运用了转化的思想;
③探索平行四边形的面积时,利用割补法,将平行四边形剪切成长方形,运用了转化的思想;
④求圆柱的体积,利用割补法,将圆柱沿着底面半径和高切拼成小长方体,运用了转化的思想。
①②③④都运用了转化的思想。
故答案为:D
【点睛】本题是考查分数除法、小数乘法的计算方法,平行四边形面积公式的推导,圆柱的体积公式的推导,关键是利用“转化”思想解决问题。
3.B
【分析】等底等高的圆锥的体积是圆柱体积的。把圆柱削成一个体积最大的圆锥,那么圆锥和圆柱为等底等高,则圆锥的体积是圆柱体积的,那么削去部分的体积是圆柱体积的,据此即可算出削去部分的体积。
【详解】由分析可知:24×(1-)
=24×
=16(m )
削去部分的体积是16m 。
故答案为:B
【点睛】此题考查等底等高的圆柱与圆锥的体积关系,要求学生能根据它们之间的数量关系解决实际问题。
4.A
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】12.56×9×
=113.04×
=37.68(cm3)
一个高是9cm,底面积是12.56cm2的圆锥,它的体积是37.68cm3。
故答案为:A
【点睛】熟练掌握圆锥的体积公式是解答本题的关键。
5.C
【分析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高也相等时,圆锥的底面积是圆柱底面积的3倍;据此解答。
【详解】36×3=108(平方厘米)
圆锥的底面积是108平方厘米。
故答案为:C
【点睛】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用。
6.A
【分析】已知一根圆柱形输油管,内直径是4dm(40cm),油在输油管内的形状是圆柱形,油在管内的流速是4 dm/s(40cm/s),相当于圆柱的高;由此可利用圆柱的体积公式V=sh求出每秒流油的体积;据此解答。
【详解】4dm=40cm,4 dm/s=40cm/s,
3.14×(40÷2)2×40
=3.14×400×40
=1256×40
=50240(cm3)
每秒流过的油是50240 cm3。
故答案为:A
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
7. 90π 60
【分析】根据圆柱的体积公式即可求出长方体的体积,表面积比原来增加了两个长方形的面积。
【详解】体积为:
π×32×10
=π×9×10
=90π(立方厘米)
表面积比原来增加了:
10×3×2
=30×2
=60(平方厘米)
它的体积是90π立方厘米,表面积比原来增加了60平方厘米。
【点睛】本题考查了认识立体图形,熟练掌握圆柱的体积公式和长方体的表面积公式是关键。
8.6.28
【分析】把圆柱拼成一个近视长方体,表面积就是增加了两个长是圆柱的高,宽是圆柱底面半径的两个长方形的面积,根据长方形面积公式:面积=长×宽,宽=面积÷长,求出圆柱底面半径,再根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【详解】400÷2÷20
=200÷20
=10(cm)
3.14×102×20
=3.14×100×20
=314×20
=6280(cm3)
6280cm3=6.28dm3
把一个圆柱切开拼成一个近似的长方体,拼成后的长方体的表面积比圆柱的表面积增加400cm3,已知圆柱高是20cm,圆柱体积是6.28dm3。
【点睛】解答本题的关键明确表面积增加了两个长是圆柱的高,宽是圆柱的半径的长方形的面积,注意单位名数的换算。
9.5厘米
【详解】略
10. 3 4
【分析】结合题意,把圆柱的底面半径看作1,则圆锥的底面半径就是2,设它们的高都为h;分别求出圆锥、圆柱的体积,即可求得它们的体积比。
【详解】设圆柱的底面半径为1,则圆锥的底面半径为2,它们的高相等,记为h,则圆锥的体积=×22×πh=πh,圆柱的体积=πh;
πh∶πh
=(πh÷πh)∶(πh÷πh)
=1∶
=3∶4
高相等,底面半径之比是1∶2的圆柱与圆锥,它们的体积之比是3∶4。
【点睛】此题考查了圆锥和圆柱的体积公式的实际应用。
11.10
【分析】等底等高的圆锥的体积是圆柱的体积的倍,由此即可求出圆锥的体积解决问题。
【详解】30×=10(立方米)
圆锥体积是10立方米。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
12.3000
【分析】根据题意可知,把这个圆柱截成3段,需要截2次,每截一次就增加两个截面,由此可知,表面积增加的是4个截面的面积,据此可以求出圆柱的底面积,然后根据圆柱的体积公:V=Sh,把数据代入公式解答。
【详解】2米=200厘米
60÷4×200
=15×200
=3000(cm3)
原来圆柱形木料的体积是3000cm3。
【点睛】此题主要考查圆柱的表面积公式、体积公式的灵活用,关键是熟记公式。
13.√
【分析】根据圆柱体的特征,它的上下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形或正方形,长方形的长等于圆柱体的底面周长,宽等于圆柱体的高;由此解答。
【详解】根据圆柱体的侧面展开图的长、宽与圆柱体的底面周长和高的关系,如果圆柱的侧面展开后是一个正方形,那么这个圆柱的高和底面周长一定相等。原题的说法正确。
故答案为:√
【点睛】此题主要考查圆柱的特征,以及侧面展开图的长、宽与圆柱体的底面周长和高的关系。
14.×
【分析】根据圆柱的体积公式:体积=底面积×高;用一张长方形纸围成不同的两个圆柱,如果长等于宽,则围成的两个圆柱的体积相等;如果长和宽不相等,两个圆柱的底面半径不同,高也不同,所以它们的体积不相等,据此解答。
【详解】根据分析可知,用一张长方形纸能围成不同的两个圆柱,它们的体积不一定相等。
原题干说法错误。
故答案为:×
【点睛】根据长方形的特征以及圆柱的体积公式进行解答。
15.√
【分析】把圆柱形木料锯成长短不同的三小段圆柱形木料,增加4个底面圆的面积。根据圆的面积公式:面积=π×半径2,代入数据,求出一个底面圆的面积,再乘4,再进行比较,即可解答。
【详解】3.14×32×4
=3.14×9×4
=28.26×4
=113.04(dm2)
一段长是12dm底面半径是3dm的圆柱形木料,把它锯成长短不同三小段圆柱形木料,表面积比原来增加了113.04dm2。
原题干说法正确。
故答案为:√
【点睛】圆柱每锯一次,会增加两个圆的面积。如果沿圆柱的底面直径切割,会增加两个长方形的面积。
16.√
【分析】根据圆柱体积公式:V=Sh,圆锥体积公式:V=Sh,若把圆锥体积看作单位“1”,则同底等高的圆柱体积是该圆锥体积的3倍,所以当圆柱和圆锥的体积相等、底面积也相等时,圆锥的高就是圆柱高的3倍,据此解答即可。
【详解】由分析可得:
同底等高时,圆柱高是7厘米,
则圆锥高为:7×3=21(厘米)
综上所述:一个圆柱形橡皮泥的高是7厘米,把它捏成底面半径相同的圆锥,这个圆锥的高是21厘米。
故答案为:√
【点睛】本题考查了同底等高的圆柱和圆锥体积之间的关系,熟记圆柱和圆锥的体积公式是解题的关键。
17.√
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,用体积差除以倍数差,即可求出一倍数,即圆锥体积。再用圆锥体积×3=圆柱体积,据此解题即可。
【详解】圆锥体积为:
24÷(3-1)
=24÷2
=12(dm3)
圆柱体积为:
12×3=36(dm3)
故答案为:√
【点睛】此题解题的关键是理解等底等高的圆柱和圆锥体积之间的关系。
18.151.62dm2
【分析】由图可知:这个半圆柱的表面积包括一个长方形的面积,圆柱的侧面积的一半及上下两个半圆的面积之和就是一个底面积;根据圆柱的表面积公式:,其中,,,代入数据进行计算即可。
【详解】
19.94.2cm3
【分析】本题可以看作是求一个底面直径为6cm,高为(4+6)cm的圆锥的体积,圆锥的体积公式:V=πr2h,把数据代入公式求出即可。
【详解】×3.14×(6÷2)2×(4+6)
=3.14×3×10
=94.2(cm3)
20.753.6立方厘米;1381.6平方厘米
【分析】根据作图可知,是由一个圆柱和一个圆锥组成,根据圆柱的体积公式:底面积×高,圆锥的体积同时:底面积×高÷3,把数代入即可求解;
第二个图的表面积:相当于下面一个圆柱的表面积加上上面圆柱的侧面积,根据圆柱的侧面积公式:底面周长×高,圆柱的底面面积:S=πr2,把数代入公式,把两个圆柱的侧面积相加,再加两个下面圆柱的底面积即可求解。
【详解】第一个:
3.14×(6÷2)2×20+3.14×(12÷2)2×5÷3
=3.14×9×20+3.14×36×5÷3
=565.2+188.4
=753.6(立方厘米)
第二个:
3.14×(20÷2)2×2+3.14×20×8+3.14×8×10
=3.14×100×2+3.14×160+3.14×80
=628+502.4+251.2
=1381.6(平方厘米)
21.18840千克
【分析】要求这个粮囤能装稻谷的重量,先求得粮囤的体积,粮囤的形状是圆锥形的,利用圆锥的体积公式:求得体积,再进一步求得稻谷的重量。问题得解。
【详解】12.56÷3.14÷2
=4÷2
=2(米)
2×2×3.14××9×500
=12.56×3×500
=37.68×500
=18840(千克)
答:这个粮囤大约可存18840千克稻谷。
【点睛】此题主要考查学生对圆锥的体积计算公式掌握与运用情况。
22.(1)150.72立方厘米
(2)12cm
【分析】分析条件后可得出“铁块的体积=水面下降后减少的水那一部分的体积”,则求这块铁块的体积是多少,也就是求周长是25.12厘米,高是3厘米的圆柱形容器里水的体积,先求出此圆柱的半径,再根据圆柱的体积公式V=πr2h解答即可;要求圆锥的高根据圆锥的体积公式:V=πr2h,那么h=V÷÷πr2,把数据代入公式解答。
【详解】(1)25.12÷3.14÷2
=8÷2
=4(cm)
42×3.14×3
=16×3.14×3
=50.24×3
=150.72(cm3)
答:这块铁块的体积是150.72立方厘米。
(2)150.72×3÷37.68
=452.16÷37.68
=12(cm)
答:这块铁块高12厘米。
【点睛】本题主要考查不规则物体体积的求法,关键明确求这块铁块的体积,也就是求底面周长是25.12厘米的圆柱的半径,再求出高是3厘米的圆柱形容器里水的体积。
23.(1)②③;
(2)75.36平方分米;
(3)62.8升
【分析】(1)要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长,与之相配的是②号和③号;
(2)由于水桶无盖,使用只求这个圆柱的一个底面和侧面的总面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=ch,把数据代入公式解答;
(3)求水桶的容积就是求底面周长是12.56分米,高是5分米的圆柱的体积。
【详解】(1)要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长,
2号周长是:3.14×4=12.56(分米)
4号周长是:
2×3.14×3
=6.28×3
=18.84(分米)
所以相配的是②号和③号。
(2)3.14×(4÷2)2+3.14×4×5
=3.14×4+12.56×5
=12.56+62.8
=75.36(平方分米)
答:你选择的材料制成水桶需要铁皮75.36平方分米。
(3)3.14×(4÷2)2×5
=3.14×4×5
=3.14×20
=62.8(立方分米)
=62.8(升)
答:你选择的材料制成的水桶最多能装水62.8升。
【点睛】本题主要考查了圆柱的体积公式V=Sh=πr2h在实际生活中的应用。
24.62.8立方分米
【分析】截成相等的4段后,表面积增加(4-1)×2=6个底面面积,总增加的面积÷底面个数求出木材底面面积,再代入体积公式:V=Sh计算即可。
【详解】2米=20分米
(4-1)×2
=3×2
=6(个)
18.84÷6×20
=3.14×20
=62.8(立方分米)
答:原来这根圆木的体积是62.8立方分米。
【点睛】本题主要考查圆柱的体积公式,明确截成4段后,增加6个底面面积是解题的关键。
25.0.5厘米
【分析】把圆锥的底面半径看作单位“1”,高比底面直径少,也就是高相当于底面直径的(1-),根据一个数乘分数的意义,用乘法求出圆锥的高,再根据圆锥的体积公式: 求出圆锥铁块的体积,然后根据圆柱的体积公式:,用圆锥铁块的体积除以圆柱形容器的底面积就是水面上升的高度。
【详解】圆锥体铁块的高:
5×2×(1-)
=10×
=6(厘米)
圆锥体铁块的体积:
=
=
=157(立方厘米)
圆柱的底面积:
=
=314(平方厘米)
157÷314=0.5(厘米)
答:铁块放入后水面会上升0.5厘米。
【点睛】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
26.厘米
【分析】由于圆锥的底面直径比圆柱底面直径少,则圆锥的底面直径相当于圆柱的:1-,单位“1”已知,用乘法,即10×(1-)=6(厘米)。由于物体完全浸没在水中,水面上升到13厘米,根据公式:容器的底面积×水面变化的高度=物体的体积,即用圆柱的底面积×(13-12),求出圆锥的体积,再根据圆锥的体积公式:底面积×高×,把数代入公式即可求出圆锥形钢材的高。
【详解】10×(1-)
=10×
=6(厘米)
6÷2=3(厘米)
10÷2=5(厘米)
3.14×5×5×(13-12)
=78.5×1
=78.5(立方厘米)
78.5×3÷(3.14×3×3)
=78.5×3÷3.14÷3÷3
=78.5÷3.14÷3
=25÷3
=(厘米)
答:圆锥形钢材的高是厘米。
【点睛】本题主要考查圆柱和圆锥的体积公式,熟练掌握它们的体积公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
