平行线的特征(河北省张家口市桥西区)
文档属性
| 名称 | 平行线的特征(河北省张家口市桥西区) |

|
|
| 格式 | rar | ||
| 文件大小 | 487.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-10 00:00:00 | ||
图片预览




文档简介
课件17张PPT。平行线的特征授课人:张家口市第十六中学
张广雄
复习回顾: 直线平行的条件
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
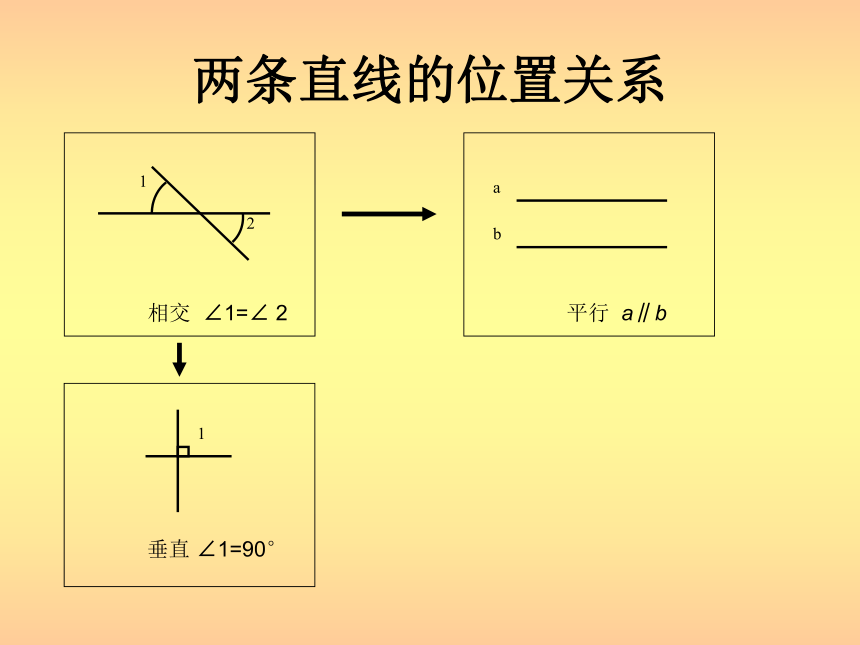
两条直线的位置关系 两条平行线被第三条直线所截 图中共几个角?
答:8个角
你能找到几对同位角?
答:①∠1和∠5
②∠2和∠6
③∠3和∠8
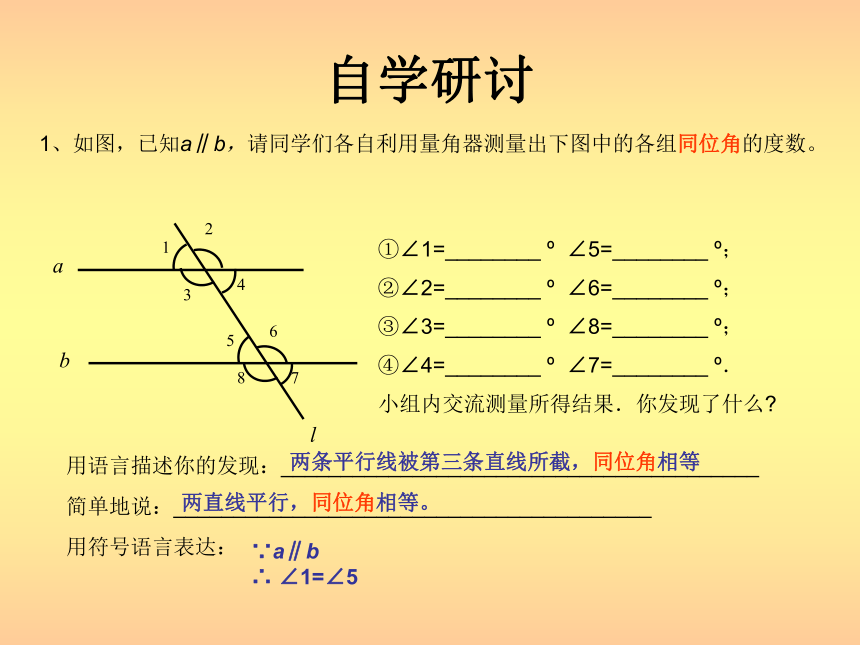
④∠4和∠7自学研讨 1、如图,已知a∥b,请同学们各自利用量角器测量出下图中的各组同位角的度数。 ①∠1=________ o ∠5=________ o;
②∠2=________ o ∠6=________ o;
③∠3=________ o ∠8=________ o;
④∠4=________ o ∠7=________ o.
小组内交流测量所得结果.你发现了什么?用语言描述你的发现:________________________________________两条平行线被第三条直线所截,同位角相等简单地说:________________________________________两直线平行,同位角相等。用符号语言表达:∵a∥b
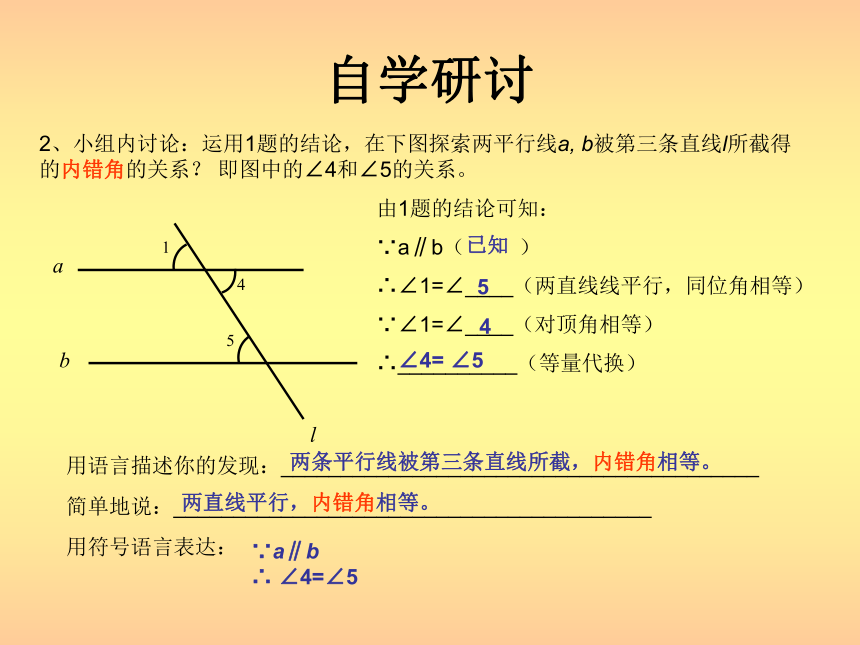
∴ ∠1=∠5 1自学研讨2、小组内讨论:运用1题的结论,在下图探索两平行线a, b被第三条直线l所截得的内错角的关系? 即图中的∠4和∠5的关系。45abl由1题的结论可知:
∵a∥b( )
∴∠1=∠____(两直线线平行,同位角相等)
∵∠1=∠____(对顶角相等)
∴__________(等量代换)用语言描述你的发现:________________________________________两条平行线被第三条直线所截,内错角相等。简单地说:________________________________________两直线平行,内错角相等。用符号语言表达:∵a∥b
∴ ∠4=∠5 已知54∠4= ∠5自学研讨3、小组内讨论:运用1题的结论,在下图探索两平行线a, b被第三条直线所截得的同旁内角的关系?即图中的∠3和∠5的关系。 135abl由1题的结论可知:
∵_______( )
∴∠1=∠____( )
∵∠1+∠3=____(邻补角)
∴∠5+∠3=____(等量代换)用语言描述你的发现:________________________________________两条平行线被第三条直线所截,同旁内角互补简单地说:________________________________________两直线平行,同旁内角互补。用符号语言表达:∵a∥b
∴ ∠3+∠5=180° a∥b已知5两直线平行,同位角相等180°180°探索归纳 平行线的特征:1、两直线平行,同位角相等。
∵a∥b
∴ ∠1=∠5 ,∠2=∠6
∠3=∠8 ,∠4=∠72、两直线平行,内错角相等。
∵a∥b
∴ ∠3=∠6,∠4=∠53、两直线平行,同旁内角互补。
∵a∥b
∴ ∠3+∠5=180°
∠4+∠6=180°展示风采 1. 如图,已知直线a∥b,∠1=45°,求∠2的度数。21ab解 ∵a∥b(已知)∴∠1=∠2(两直线平行,同位角相等)
∵∠1=45°(已知)∴∠2=45°(等量代换)展示风采2. 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数.能否求得∠A的度数??解 ∵AB∥CD (已知)∴ ∠B+∠C=180° (两直线平行,同旁内角互补)∵∠B=60°(已知)∴ ∠C=120° (等式性质)ABCD思考:
1、∠A和∠B是不是同旁内角?
2、它们是哪两条直线被哪一条直线截得的同旁内角?
3、已知里告诉了AD和BC平行吗?
4、∠A和∠B互补吗?为什么?
5、我们能求出A的度数吗?根据题目的已知条件,无法求出∠A的度数. 1课堂检测 1.如图,( 20分)
(1) ∵AD∥BC(已知),
∴ ∠B=∠1( );
(2) ∵AB∥CD(已知),
∴∠D=∠1 ( ) .ABDC两直线平行,同位角相等两直线平行,内错角相等课堂检测2.如图, ( 20分)
(1) ∵AD∥BC(已知),
∴ ( ) +∠ABC =180°(两直线平行,同旁内角互补);
(2) ∵AB∥CD(已知),
∴ ( ) +∠ABC = 180° (两直线平行,同旁内角互补);ABDC∠ BAD∠ BCD课堂检测3.在图上来着与第三条直线相交的两条平行线,如果∠ 1=50°,那么
∠ 2=_____; ∠ 3=_____; ∠ 4=_____; ( 20分)50°130°50°4123解∵∠3=120°( ),
又∵∠3=∠1( ),
∴∠1 =( )( );
∵a∥b( ),
∴∠1+∠2 =180°( );
∴∠2 =( )(等式的性质)。课堂检测4.如图,已知直线a∥b,∠3=120°,求∠1、∠2的度数,抄写下面的解答过程,并填空或填写理由。 ( 20分)21a3b已知对顶角相等120 °等量代换已知两直线平行,同旁内角互补60°整理 小结 请同学们谈谈你这堂课的收获 ?一、知识方面的收获。
二、方法和能力方面的收获。 三、其它方面的收获。 平行线的特征: 1、两直线平行,同位角相等;
2、两直线平行,内错角相等;
3、两直线平行,同旁内角补。
1、可以通过测量实验的方法来研究图形的规律。……谢谢! 再见!
张广雄
复习回顾: 直线平行的条件
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
两条直线的位置关系 两条平行线被第三条直线所截 图中共几个角?
答:8个角
你能找到几对同位角?
答:①∠1和∠5
②∠2和∠6
③∠3和∠8
④∠4和∠7自学研讨 1、如图,已知a∥b,请同学们各自利用量角器测量出下图中的各组同位角的度数。 ①∠1=________ o ∠5=________ o;
②∠2=________ o ∠6=________ o;
③∠3=________ o ∠8=________ o;
④∠4=________ o ∠7=________ o.
小组内交流测量所得结果.你发现了什么?用语言描述你的发现:________________________________________两条平行线被第三条直线所截,同位角相等简单地说:________________________________________两直线平行,同位角相等。用符号语言表达:∵a∥b
∴ ∠1=∠5 1自学研讨2、小组内讨论:运用1题的结论,在下图探索两平行线a, b被第三条直线l所截得的内错角的关系? 即图中的∠4和∠5的关系。45abl由1题的结论可知:
∵a∥b( )
∴∠1=∠____(两直线线平行,同位角相等)
∵∠1=∠____(对顶角相等)
∴__________(等量代换)用语言描述你的发现:________________________________________两条平行线被第三条直线所截,内错角相等。简单地说:________________________________________两直线平行,内错角相等。用符号语言表达:∵a∥b
∴ ∠4=∠5 已知54∠4= ∠5自学研讨3、小组内讨论:运用1题的结论,在下图探索两平行线a, b被第三条直线所截得的同旁内角的关系?即图中的∠3和∠5的关系。 135abl由1题的结论可知:
∵_______( )
∴∠1=∠____( )
∵∠1+∠3=____(邻补角)
∴∠5+∠3=____(等量代换)用语言描述你的发现:________________________________________两条平行线被第三条直线所截,同旁内角互补简单地说:________________________________________两直线平行,同旁内角互补。用符号语言表达:∵a∥b
∴ ∠3+∠5=180° a∥b已知5两直线平行,同位角相等180°180°探索归纳 平行线的特征:1、两直线平行,同位角相等。
∵a∥b
∴ ∠1=∠5 ,∠2=∠6
∠3=∠8 ,∠4=∠72、两直线平行,内错角相等。
∵a∥b
∴ ∠3=∠6,∠4=∠53、两直线平行,同旁内角互补。
∵a∥b
∴ ∠3+∠5=180°
∠4+∠6=180°展示风采 1. 如图,已知直线a∥b,∠1=45°,求∠2的度数。21ab解 ∵a∥b(已知)∴∠1=∠2(两直线平行,同位角相等)
∵∠1=45°(已知)∴∠2=45°(等量代换)展示风采2. 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数.能否求得∠A的度数??解 ∵AB∥CD (已知)∴ ∠B+∠C=180° (两直线平行,同旁内角互补)∵∠B=60°(已知)∴ ∠C=120° (等式性质)ABCD思考:
1、∠A和∠B是不是同旁内角?
2、它们是哪两条直线被哪一条直线截得的同旁内角?
3、已知里告诉了AD和BC平行吗?
4、∠A和∠B互补吗?为什么?
5、我们能求出A的度数吗?根据题目的已知条件,无法求出∠A的度数. 1课堂检测 1.如图,( 20分)
(1) ∵AD∥BC(已知),
∴ ∠B=∠1( );
(2) ∵AB∥CD(已知),
∴∠D=∠1 ( ) .ABDC两直线平行,同位角相等两直线平行,内错角相等课堂检测2.如图, ( 20分)
(1) ∵AD∥BC(已知),
∴ ( ) +∠ABC =180°(两直线平行,同旁内角互补);
(2) ∵AB∥CD(已知),
∴ ( ) +∠ABC = 180° (两直线平行,同旁内角互补);ABDC∠ BAD∠ BCD课堂检测3.在图上来着与第三条直线相交的两条平行线,如果∠ 1=50°,那么
∠ 2=_____; ∠ 3=_____; ∠ 4=_____; ( 20分)50°130°50°4123解∵∠3=120°( ),
又∵∠3=∠1( ),
∴∠1 =( )( );
∵a∥b( ),
∴∠1+∠2 =180°( );
∴∠2 =( )(等式的性质)。课堂检测4.如图,已知直线a∥b,∠3=120°,求∠1、∠2的度数,抄写下面的解答过程,并填空或填写理由。 ( 20分)21a3b已知对顶角相等120 °等量代换已知两直线平行,同旁内角互补60°整理 小结 请同学们谈谈你这堂课的收获 ?一、知识方面的收获。
二、方法和能力方面的收获。 三、其它方面的收获。 平行线的特征: 1、两直线平行,同位角相等;
2、两直线平行,内错角相等;
3、两直线平行,同旁内角补。
1、可以通过测量实验的方法来研究图形的规律。……谢谢! 再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
