北师大版六年级数学 第二学期 第一单元质量检测卷(无答案)
文档属性
| 名称 | 北师大版六年级数学 第二学期 第一单元质量检测卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 866.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:59:17 | ||
图片预览

文档简介
第一单元质量检测卷
六年级数学·BS·下册
(时间:90分钟 满分:100分)
题号 一 二 三 四 五 六 总分
得分
一、填空题。 (每空1分,共25 分)
1.圆柱的底面是两个完全一样的( ),把圆柱的侧面沿着高剪开,得到的长方形的长是圆柱的( ),宽是圆柱的( )。
2.一个圆柱的侧面展开图是一个边长为 12.56 厘米的正方形,这个圆柱的侧面积是( )平方厘米,它的表面积是( )平方厘米。
3.如右图,以b为轴旋转一周,可以得到一个( ),a是它的( ),b是它的( )。
4.两个底面积相等的圆柱,一个圆柱的高是 3.2 厘米,体积是 240 立方厘米,若另一个圆柱的高是 6 厘米,则体积是( )立方厘米。
5.把一个棱长为6 厘米的正方体削成一个最大的圆柱,这个圆柱的底面积是( ),体积是( ),削去部分的体积占正方体体积的( )%。
6.一个圆锥和一个圆柱等底等高,它们的体积之和是64 立方厘米,圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
7.一个圆锥形木料,底面直径 12 厘米、高 8 厘米,沿着直径将它锯成两半之后,表面积增加了( )平方厘米。
8.做一个底面直径 10 厘米、高 1.2 分米的无盖铁皮圆筒,至少需要( )平方厘米的铁皮。 (接头处忽略不计)
9.右图这个玻璃酒杯最多能装( )毫升的酒。
10.把一根长 20 厘米的圆木锯成3个小圆柱体。表面积比原来增加了 12.56平方厘米,这个圆木的体积是( )立方厘米。
11.5 平方米3 平方分米=( )平方分米=( )平方米4200 立方厘米=( )立方分米=( )升
3.052立方米=( )立方分米
4.05 升=( )升( )毫升
二、判断题。 (每题1分,共5分)
1.圆锥的体积比圆柱的体积小。 ( )
2.如果把一个圆柱截成2段,那么体积和表面积与原来相比都增加了。
( )
3.圆锥的底面直径扩大到原来的 3 倍,高扩大到原来的 2 倍,则圆锥的体积扩大到原来的 9 倍。 ( )
4.底面直径和高都是 2 厘米的圆柱,它的体积和侧面积相等。 ( )
5.任意一个三角形绕一条边旋转都能形成一个圆锥。 ( )
三、选择题。 (每题2 分,共 12 分)
1.一个 圆柱的侧面展开图是一个正方形,这个圆柱的底面 直径与高的比是( )。
A.2 : π B.1 : π C.π : 1
2.一个装满水的圆锥形容器高12厘米,将这些水倒入与它等底等高的圆柱形容器里,杯中的水深( )厘米。
A.4 B.6 C.36
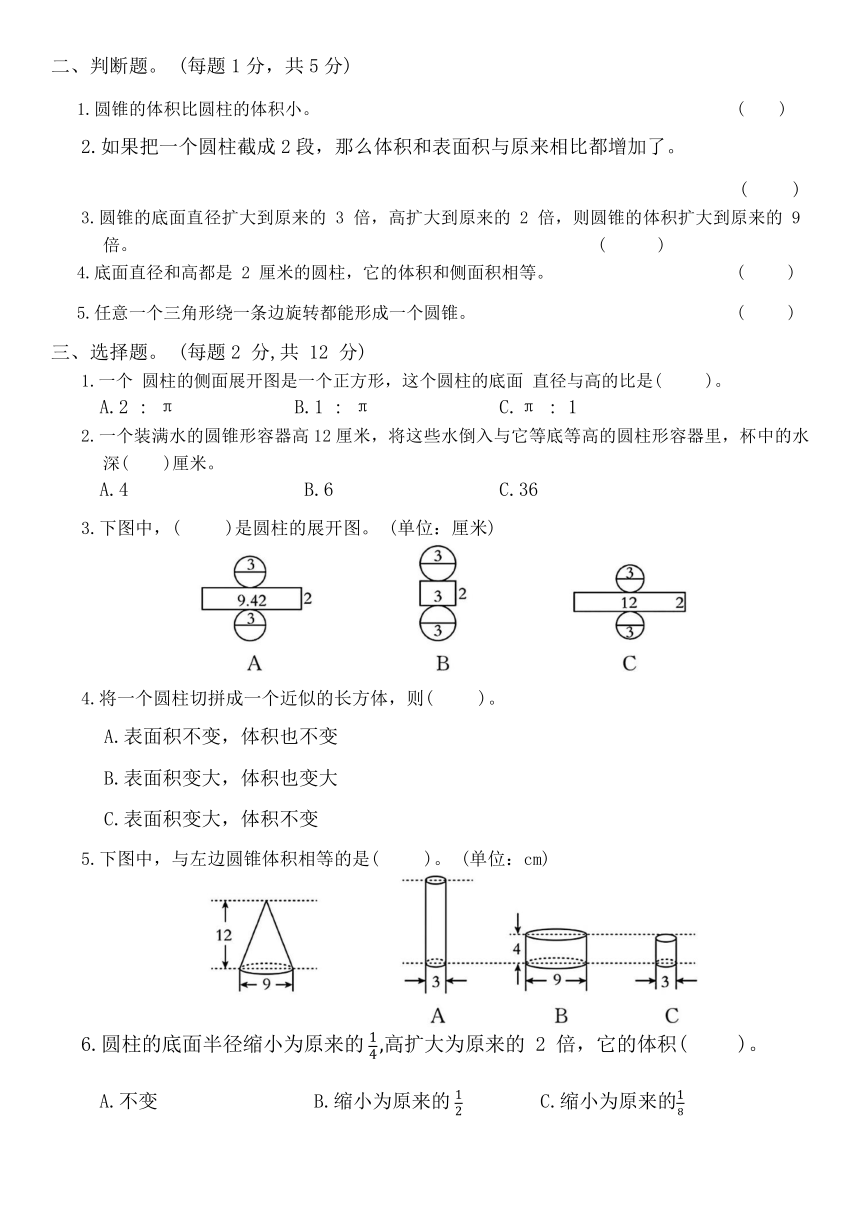
3.下图中,( )是圆柱的展开图。 (单位:厘米)
4.将一个圆柱切拼成一个近似的长方体,则( )。
A.表面积不变,体积也不变
B.表面积变大,体积也变大
C.表面积变大,体积不变
5.下图中,与左边圆锥体积相等的是( )。 (单位:cm)
6.圆柱的底面半径缩小为原来的 高扩大为原来的 2 倍,它的体积( )。
A.不变 B.缩小为原来的 C.缩小为原来的
四、计算题。(共 18 分)
1.计算下面首饰盒的表面积。 (4分)
2.计算下面图形的体积。 (6 分)
3.如图,在圆柱里挖去一个最大的圆锥,求剩下部分的体积。 (4分)
4.如图是一个长方形铁皮(每个方格的边长表示 1 分米,)剪下图中的涂色部分可以围成一个圆柱体,这个圆柱体的体积是多少 (4分)
五、填表题。 (16 分)
名称 底面半径//cm 高/cm 侧面积/cm 表面积//cm 体积/cm
圆柱 ① 3 8
② 5 25.12
圆锥 ③ 5 2.7 ——— ——
④ 4 1.8 —— ——
六、解决问题。(共24 分)
1.淘气制作了一个圆柱形笔筒(如图),他想给这个笔筒的侧面和底面贴上彩纸,至少需要多少彩纸 (4分)
2.某粮仓如图所示。其中圆柱部分的底面周长是 31.4 米,高是 4 米,圆锥部分的高是1.5 米。这个粮仓最多能装多少立方米的粮食 (厚度忽略不计)
(5分)
3.一个圆柱形塑料桶(如图所示),底面直径是 4 分米,高是5 分米。 如果桶里所盛水占桶的容积的90%,那么这桶水大约有多少升 (5 分)
4.一台压路机的前轮是圆柱形,轮宽1.5米,直径 1.2 米。 压路机的前轮每分钟转动 20 周,匀速前进 小时压过的路面是多少平方米 (5分)
5.有一种饮料的瓶身呈圆柱形(不包括瓶颈),容积是 400 立方厘米,现在瓶中装有一些饮料,正放时饮料的高度是 20 厘米,倒放时空余部分的高度为5厘米。瓶内现有饮料多少立方厘米 (5分)
六年级数学·BS·下册
(时间:90分钟 满分:100分)
题号 一 二 三 四 五 六 总分
得分
一、填空题。 (每空1分,共25 分)
1.圆柱的底面是两个完全一样的( ),把圆柱的侧面沿着高剪开,得到的长方形的长是圆柱的( ),宽是圆柱的( )。
2.一个圆柱的侧面展开图是一个边长为 12.56 厘米的正方形,这个圆柱的侧面积是( )平方厘米,它的表面积是( )平方厘米。
3.如右图,以b为轴旋转一周,可以得到一个( ),a是它的( ),b是它的( )。
4.两个底面积相等的圆柱,一个圆柱的高是 3.2 厘米,体积是 240 立方厘米,若另一个圆柱的高是 6 厘米,则体积是( )立方厘米。
5.把一个棱长为6 厘米的正方体削成一个最大的圆柱,这个圆柱的底面积是( ),体积是( ),削去部分的体积占正方体体积的( )%。
6.一个圆锥和一个圆柱等底等高,它们的体积之和是64 立方厘米,圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
7.一个圆锥形木料,底面直径 12 厘米、高 8 厘米,沿着直径将它锯成两半之后,表面积增加了( )平方厘米。
8.做一个底面直径 10 厘米、高 1.2 分米的无盖铁皮圆筒,至少需要( )平方厘米的铁皮。 (接头处忽略不计)
9.右图这个玻璃酒杯最多能装( )毫升的酒。
10.把一根长 20 厘米的圆木锯成3个小圆柱体。表面积比原来增加了 12.56平方厘米,这个圆木的体积是( )立方厘米。
11.5 平方米3 平方分米=( )平方分米=( )平方米4200 立方厘米=( )立方分米=( )升
3.052立方米=( )立方分米
4.05 升=( )升( )毫升
二、判断题。 (每题1分,共5分)
1.圆锥的体积比圆柱的体积小。 ( )
2.如果把一个圆柱截成2段,那么体积和表面积与原来相比都增加了。
( )
3.圆锥的底面直径扩大到原来的 3 倍,高扩大到原来的 2 倍,则圆锥的体积扩大到原来的 9 倍。 ( )
4.底面直径和高都是 2 厘米的圆柱,它的体积和侧面积相等。 ( )
5.任意一个三角形绕一条边旋转都能形成一个圆锥。 ( )
三、选择题。 (每题2 分,共 12 分)
1.一个 圆柱的侧面展开图是一个正方形,这个圆柱的底面 直径与高的比是( )。
A.2 : π B.1 : π C.π : 1
2.一个装满水的圆锥形容器高12厘米,将这些水倒入与它等底等高的圆柱形容器里,杯中的水深( )厘米。
A.4 B.6 C.36
3.下图中,( )是圆柱的展开图。 (单位:厘米)
4.将一个圆柱切拼成一个近似的长方体,则( )。
A.表面积不变,体积也不变
B.表面积变大,体积也变大
C.表面积变大,体积不变
5.下图中,与左边圆锥体积相等的是( )。 (单位:cm)
6.圆柱的底面半径缩小为原来的 高扩大为原来的 2 倍,它的体积( )。
A.不变 B.缩小为原来的 C.缩小为原来的
四、计算题。(共 18 分)
1.计算下面首饰盒的表面积。 (4分)
2.计算下面图形的体积。 (6 分)
3.如图,在圆柱里挖去一个最大的圆锥,求剩下部分的体积。 (4分)
4.如图是一个长方形铁皮(每个方格的边长表示 1 分米,)剪下图中的涂色部分可以围成一个圆柱体,这个圆柱体的体积是多少 (4分)
五、填表题。 (16 分)
名称 底面半径//cm 高/cm 侧面积/cm 表面积//cm 体积/cm
圆柱 ① 3 8
② 5 25.12
圆锥 ③ 5 2.7 ——— ——
④ 4 1.8 —— ——
六、解决问题。(共24 分)
1.淘气制作了一个圆柱形笔筒(如图),他想给这个笔筒的侧面和底面贴上彩纸,至少需要多少彩纸 (4分)
2.某粮仓如图所示。其中圆柱部分的底面周长是 31.4 米,高是 4 米,圆锥部分的高是1.5 米。这个粮仓最多能装多少立方米的粮食 (厚度忽略不计)
(5分)
3.一个圆柱形塑料桶(如图所示),底面直径是 4 分米,高是5 分米。 如果桶里所盛水占桶的容积的90%,那么这桶水大约有多少升 (5 分)
4.一台压路机的前轮是圆柱形,轮宽1.5米,直径 1.2 米。 压路机的前轮每分钟转动 20 周,匀速前进 小时压过的路面是多少平方米 (5分)
5.有一种饮料的瓶身呈圆柱形(不包括瓶颈),容积是 400 立方厘米,现在瓶中装有一些饮料,正放时饮料的高度是 20 厘米,倒放时空余部分的高度为5厘米。瓶内现有饮料多少立方厘米 (5分)
