三角函数复习课
图片预览



文档简介
课件25张PPT。锐角三角函数复习课一、课前小测:
1、在Rt△ABC中,∠C=90°,AC=4,BC=3
则tanA=__,cosA=__, sinA=__.
2、 在平面直角坐标系中,已知点A(2,0)和点B(0,-4),则tan∠OAB=___.
3、若sinA= ,则∠A= __;
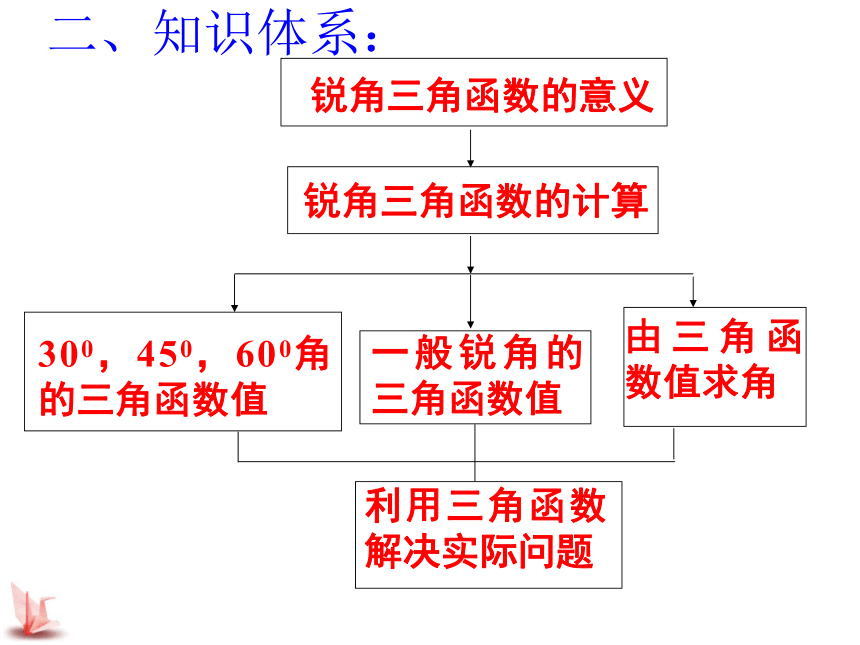
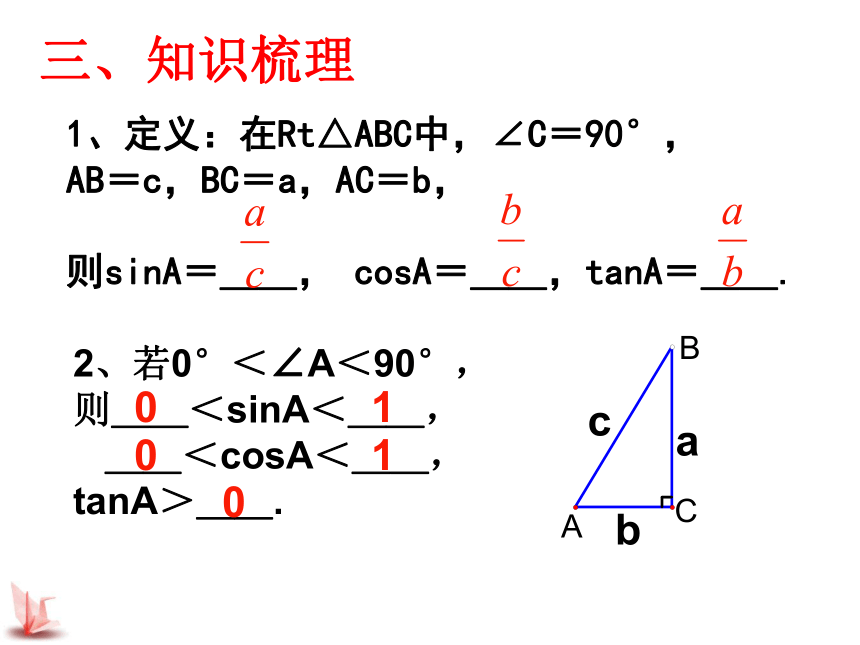
若cos(750-A)= ,则∠A= __,= .二、知识体系:锐角三角函数的意义锐角三角函数的计算300,450,600角的三角函数值一般锐角的三角函数值由三角函数值求角利用三角函数解决实际问题三、知识梳理1、定义:在Rt△ABC中,∠C=90°,
AB=c,BC=a,AC=b,
则sinA=__, cosA=__,tanA=__.
02、若0°<∠A<90°,
则__<sinA<__,
__<cosA<__,
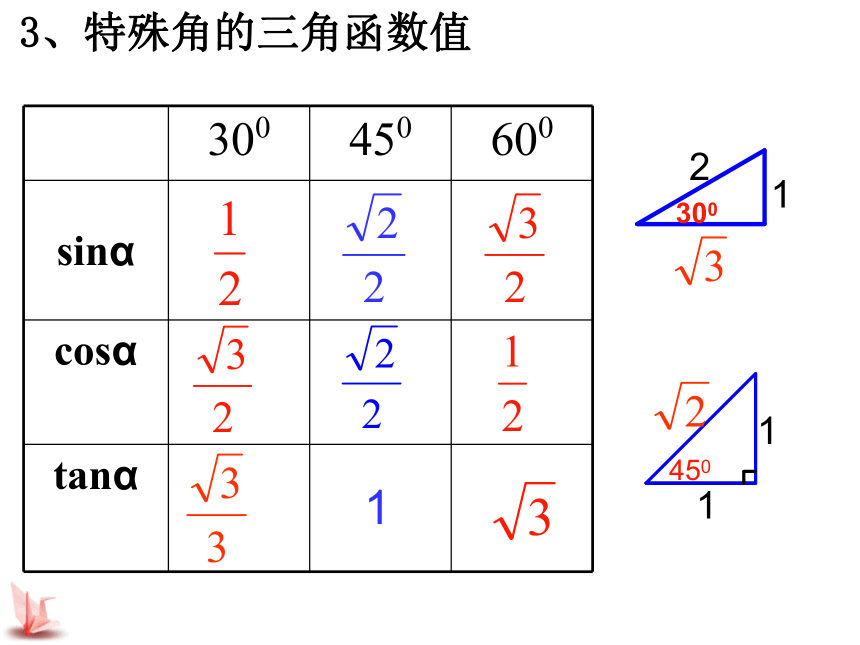
tanA>__. 10103、特殊角的三角函数值
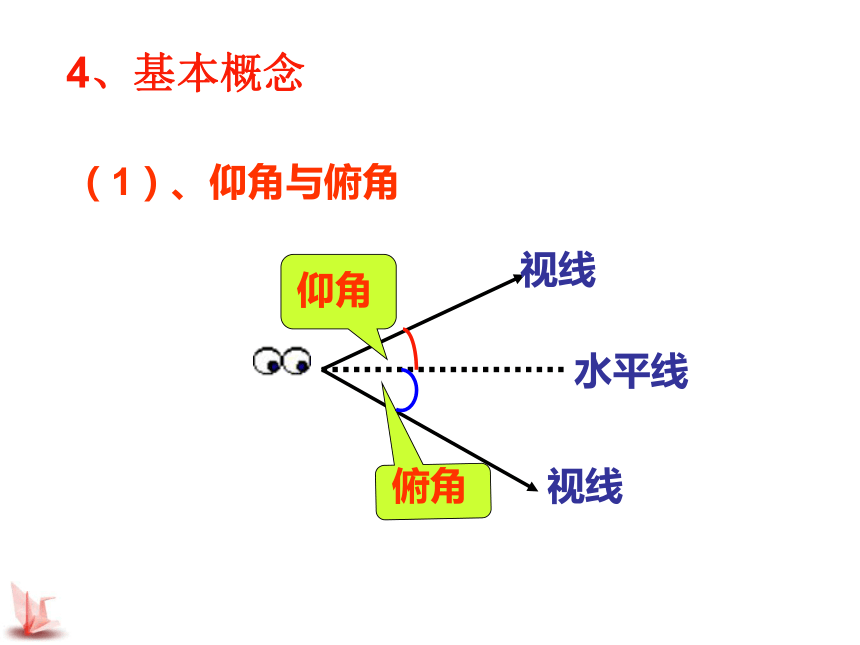
?1视线视线水平线(1)、仰角与俯角4、基本概念
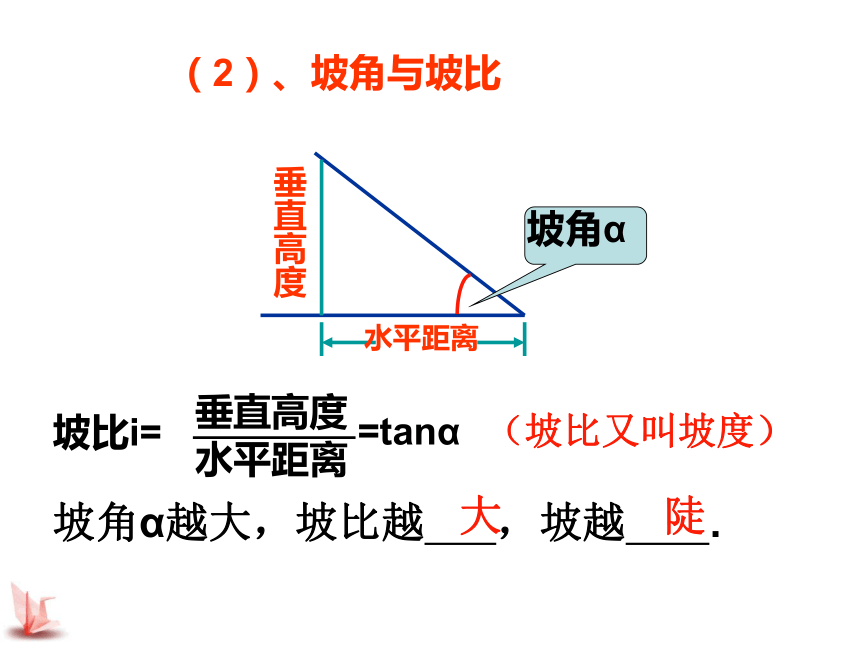
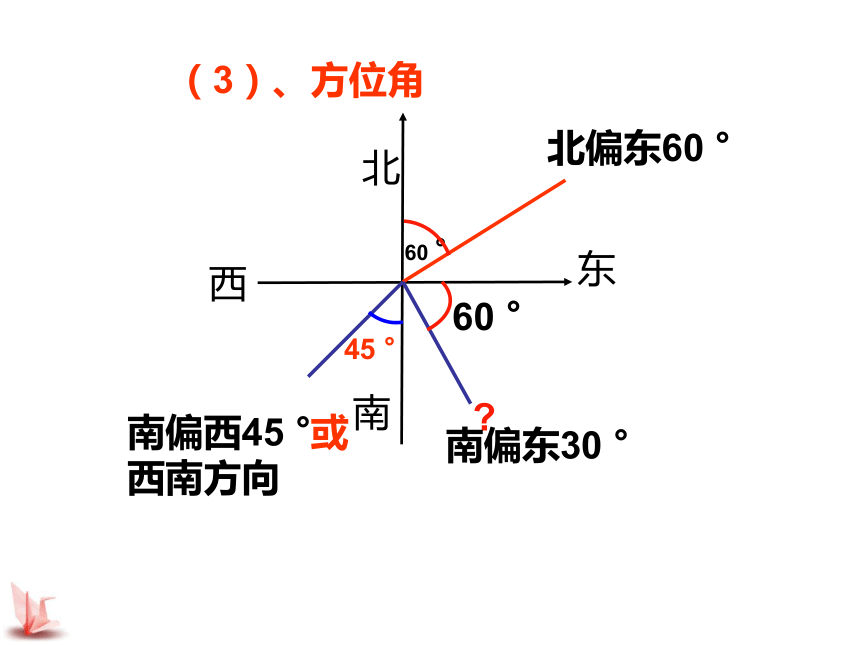
(2)、坡角与坡比垂直高度=tanα坡角α越大,坡比越 ,坡越 .大(坡比又叫坡度)陡北南西东(3)、方位角60 °北偏东60 °
45 °?南偏西45 °或西南方向60 °南偏东30 ° 一、选择题
1、△ABC中,∠C=90°,若sinA= ,则tanA等于( )
2、在△ABC中,∠C=90°, 且sinA= ,则cosB等于( )
3、在△ABC中,∠C=90°,tanA= ,则tanB等于( )巩固练习D.2DCD4、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定C5、如图,坡角∠ABC为300,则坡度是( )
A、 300 B、600
C、 D、D7.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB延长线上的D'处,那么tan∠BAD'等于( )B6、△ABC中,∠C=90°,若sin(800-A)
= ,则∠ A等于( )B8. 当 锐角A>45°时,sinA的值( )(A) (B)
(C) (D) B9.(浙江)身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出的风筝线长、线与地面的夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
A)甲的最高 B)丙的最高
C)乙的最低 D)丙的最低B2、在Rt△ABC中,∠C=90°,BC=20,sinA= ,
则AB= ,AC= ,
△ABC的面积= .二、填空题25151501、在△ABC中,若
则 △ABC为 三角形.等边3、如图△ABC中,∠ACB=90°,CD⊥AB于点D,BC=a,AC=b,AB=c,则
(1)sin ∠ACD = ,tan ∠BCD = ;
(2)若BD:AD=1:4,则tan∠BCD的值是 . 4、在等腰△ABC中,AB=AC=5,BC=6,
sinB= ,cosB= , tanB= .解三角函数有关问题关键是找Rt△或构造Rt△.
5.如图,AB是 O的直径,CD是弦,弦AD,BC交于点E,OA=3,CD=2,
则cos∠ CEA= .7.在△ABC中,AB=5, BC=13,
AD是BC 边上的高,AD=4.
则CD= , tanC= .(3)三、计算:(1) (深圳2008年中考试题16题 )112-1四、应用.
1.如图,为了测量一条河的宽度,一测量员在河岸边相距180米的P和Q两点分别测定对岸T的位置,T在P正南方向,在Q南偏西60方向,
则河宽为 米.
2、如图,身高1.5m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度.已知她与树之间的距离为6m,那
么这棵树的高度是 m.
3.某阶梯的形状如图所示,其中线段AB=BC, AB部分的坡角为450,BC部分的坡角为300,AD为1.5米.如果每个台阶的高度不超过20厘米,那么这一阶梯至少有 个台阶.
(最后一个台阶的高不足20厘米时,按一个台阶算, )13E(深圳2005第18题)、(8分)
4.大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60o,爬到楼顶D点测得塔顶B点的仰角为30o,求塔BC的高度.
600300北
(深圳2007第2 0题7分 )
5.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
D小结 这节课我的收获是…… 解三角函数有关问题关键是找Rt△或构造Rt△.
拓展思维
如图,距沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现在以15千米/时的速度沿北偏东300方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续
时间有多长?
(3)该城市受到台风影响的最大风力为几级?D
1、在Rt△ABC中,∠C=90°,AC=4,BC=3
则tanA=__,cosA=__, sinA=__.
2、 在平面直角坐标系中,已知点A(2,0)和点B(0,-4),则tan∠OAB=___.
3、若sinA= ,则∠A= __;
若cos(750-A)= ,则∠A= __,= .二、知识体系:锐角三角函数的意义锐角三角函数的计算300,450,600角的三角函数值一般锐角的三角函数值由三角函数值求角利用三角函数解决实际问题三、知识梳理1、定义:在Rt△ABC中,∠C=90°,
AB=c,BC=a,AC=b,
则sinA=__, cosA=__,tanA=__.
02、若0°<∠A<90°,
则__<sinA<__,
__<cosA<__,
tanA>__. 10103、特殊角的三角函数值
?1视线视线水平线(1)、仰角与俯角4、基本概念
(2)、坡角与坡比垂直高度=tanα坡角α越大,坡比越 ,坡越 .大(坡比又叫坡度)陡北南西东(3)、方位角60 °北偏东60 °
45 °?南偏西45 °或西南方向60 °南偏东30 ° 一、选择题
1、△ABC中,∠C=90°,若sinA= ,则tanA等于( )
2、在△ABC中,∠C=90°, 且sinA= ,则cosB等于( )
3、在△ABC中,∠C=90°,tanA= ,则tanB等于( )巩固练习D.2DCD4、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定C5、如图,坡角∠ABC为300,则坡度是( )
A、 300 B、600
C、 D、D7.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB延长线上的D'处,那么tan∠BAD'等于( )B6、△ABC中,∠C=90°,若sin(800-A)
= ,则∠ A等于( )B8. 当 锐角A>45°时,sinA的值( )(A) (B)
(C) (D) B9.(浙江)身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出的风筝线长、线与地面的夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
A)甲的最高 B)丙的最高
C)乙的最低 D)丙的最低B2、在Rt△ABC中,∠C=90°,BC=20,sinA= ,
则AB= ,AC= ,
△ABC的面积= .二、填空题25151501、在△ABC中,若
则 △ABC为 三角形.等边3、如图△ABC中,∠ACB=90°,CD⊥AB于点D,BC=a,AC=b,AB=c,则
(1)sin ∠ACD = ,tan ∠BCD = ;
(2)若BD:AD=1:4,则tan∠BCD的值是 . 4、在等腰△ABC中,AB=AC=5,BC=6,
sinB= ,cosB= , tanB= .解三角函数有关问题关键是找Rt△或构造Rt△.
5.如图,AB是 O的直径,CD是弦,弦AD,BC交于点E,OA=3,CD=2,
则cos∠ CEA= .7.在△ABC中,AB=5, BC=13,
AD是BC 边上的高,AD=4.
则CD= , tanC= .(3)三、计算:(1) (深圳2008年中考试题16题 )112-1四、应用.
1.如图,为了测量一条河的宽度,一测量员在河岸边相距180米的P和Q两点分别测定对岸T的位置,T在P正南方向,在Q南偏西60方向,
则河宽为 米.
2、如图,身高1.5m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度.已知她与树之间的距离为6m,那
么这棵树的高度是 m.
3.某阶梯的形状如图所示,其中线段AB=BC, AB部分的坡角为450,BC部分的坡角为300,AD为1.5米.如果每个台阶的高度不超过20厘米,那么这一阶梯至少有 个台阶.
(最后一个台阶的高不足20厘米时,按一个台阶算, )13E(深圳2005第18题)、(8分)
4.大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60o,爬到楼顶D点测得塔顶B点的仰角为30o,求塔BC的高度.
600300北
(深圳2007第2 0题7分 )
5.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
D小结 这节课我的收获是…… 解三角函数有关问题关键是找Rt△或构造Rt△.
拓展思维
如图,距沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现在以15千米/时的速度沿北偏东300方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续
时间有多长?
(3)该城市受到台风影响的最大风力为几级?D
