10.3三元一次方程组课件(共13张PPT) 青岛版数学七年级下册课件
文档属性
| 名称 | 10.3三元一次方程组课件(共13张PPT) 青岛版数学七年级下册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:17:03 | ||
图片预览




文档简介
(共13张PPT)
10.3 三元一次方程组
七年级下册第十单元
1.了解三元一次方程组的意义,明确解三元一次方程组的基本思路;
2.会根据方程组中未知数系数的特点,选择代入消元法或加减消元法解简单的三元一次方程组。
学习目标
学习任务:
①认识三元一次方程组
②解简单的三元一次方程组
根据“爸爸与小亮年龄之差正好等于爷爷与爸爸年龄之差”可列方程 .
根据“爷爷的年龄比小亮与爸爸年龄之和多12岁”可列方程 ,
设小亮、爸爸、爷爷的年龄分别为x岁、y岁、z岁,根据“三人年龄之和为120岁”可列方程 ,
小亮与爸爸、爷爷三人年龄之和为 120 岁,爷爷的年龄比小亮与爸爸年龄之和多12岁,爸爸与小亮年龄之差正好等于爷爷与爸爸年龄之差.他们三人的年龄分别是多少?
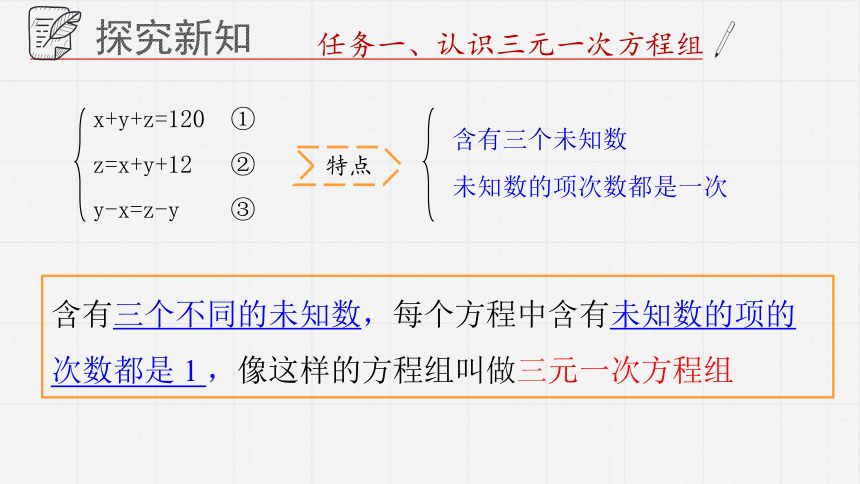
任务一、认识三元一次方程组
x+y+z=120
z=x+y+12
y-x=z-y
这个问题的解必须同时满足上面三个方程,将这三个方程联立可得一个方程组.
探究新知
含有三个不同的未知数,每个方程中含有未知数的项的次数都是 1 ,像这样的方程组叫做三元一次方程组
含有三个未知数
未知数的项次数都是一次
特点
任务一、认识三元一次方程组
探究新知
x+y+z=120 ①
z=x+y+12 ②
y-x=z-y ③
思考:三元一次方程组必须有三个方程吗?每个方程必须是三元一次方程吗?
三元一次方程组并非必须有三个方程,也并非每个方程必须是三元一次方程
√
√
即学即练
判断下列方程组是不是三元一次方程组
x+2y+z=120
3x-y+z=2
2xy-x+z=6
x+y=7
9y+x=2
x+y=13
y+z=20
x+2y+z=120
3x-y+z=21
2y-x+z=7
三元一次方程组
一元一次方程
二元一次方程组
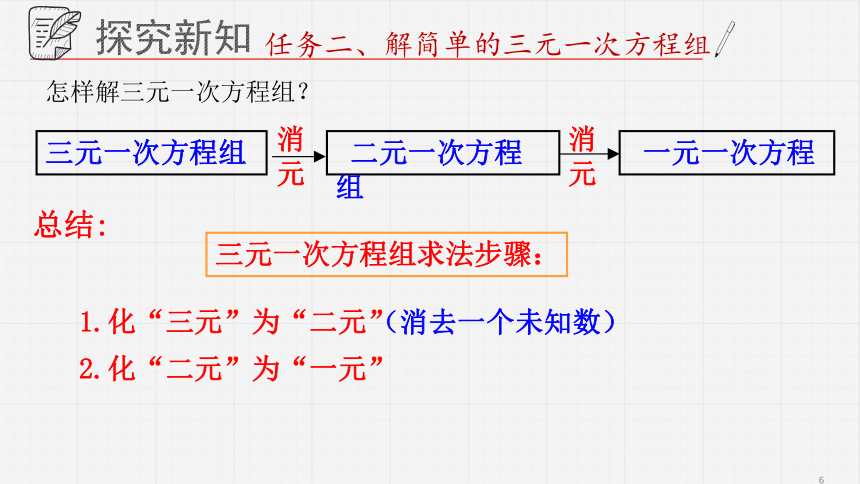
1.化“三元”为“二元”
消元
消元
三元一次方程组求法步骤:
2.化“二元”为“一元”
怎样解三元一次方程组?
(消去一个未知数)
任务二、解简单的三元一次方程组
探究新知
总结:
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
观察方程组:
考虑消去哪个未知数(也就是三个未知数要去掉哪一个 )
解法一:消去y
①+②,得 2x+2z=2
x+z=1 ④
x-z=4 ③
x+z=1 ④
解法二:消去x
2z+y=-2 ⑦
2z-y=-4 ⑧
(z+4)+y+z=2 ⑤
(z+4)-y+z=0 ⑥
化简得,
由③得,x=z+4 ④
把④代入①、②得,
解法三:消去z
把④代入①、②得
x+y+(x-4)=2 ⑤
x-y+(x-4)=0 ⑥
化简得,
由③得,z=x-4 ④
2x+y=6 ⑦
4-y= 0 ⑧
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
注:如果三个方程中有一个方程是二元一次方程(如例1中的③),则可以先对另外两个方程组进行消元,消元时就消去三个元中这个二元一次方程(如例1中的③)中缺少的那个元。缺某元,消某元。
在三元化二元时,对于具体方法的选取应该注意选择最恰当、最简便的方法。
解之,得
解: 由①+②,得
2x+2z=2,
化简,得
x+z=1 ④
由③+④,得
2x=5
x-z=4 ③
x+z= 1 ④
∴
把
代入②,得
解之,得 y=1
所以,原方程组的解是
解之,得
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
把 代入③,得
解:由③-②,得
典型例题
例2 解方程组
x+y=3 ①
y+z=5 ②
x+z=4 ③
x-y= -1 ④
由① + ④,得
解之,得
所以,原方程组的解是
把x=1代入方程①、③,分别得
x+y= 3 ①
x-y= -1 ④
联立①④得:
2x=2
x=1
y=2,z=3
x=1
y=2
z=3
在消去一个未知数得出比原方程组少一个未知数的二元一次方程组的过程中,原方程组的每一个方程一般都至少要用到一次.
例2 也可以这样解!
解:由①+②+③,得
即,
由⑤-①,得
由⑤-②,得
由⑤-③,得
典型例题
例2 解方程组
x+y=3 ①
y+z=5 ②
x+z=4 ③
2(x+y+z)= 12 ④
x+y+z= 6 ⑤
x=1
z=3
y=2
所以,原方程组的解是
x=1
y=2
z=3
课堂小结
(一)三元一次方程组的概念是什么
(二)解三元一次方程组的基本思路是什么
(三)在三元化二元时,对于具体方法的选取应该注意什么?
消元,把“三元”化为“一元”
含有三个不同的未知数,每个方程中含有未知数的项的次数都是 1 ,像这样的方程组叫做三元一次方程组
缺某元,消某元。
课后作业
作业:
P60练习 10.3
10.3 三元一次方程组
七年级下册第十单元
1.了解三元一次方程组的意义,明确解三元一次方程组的基本思路;
2.会根据方程组中未知数系数的特点,选择代入消元法或加减消元法解简单的三元一次方程组。
学习目标
学习任务:
①认识三元一次方程组
②解简单的三元一次方程组
根据“爸爸与小亮年龄之差正好等于爷爷与爸爸年龄之差”可列方程 .
根据“爷爷的年龄比小亮与爸爸年龄之和多12岁”可列方程 ,
设小亮、爸爸、爷爷的年龄分别为x岁、y岁、z岁,根据“三人年龄之和为120岁”可列方程 ,
小亮与爸爸、爷爷三人年龄之和为 120 岁,爷爷的年龄比小亮与爸爸年龄之和多12岁,爸爸与小亮年龄之差正好等于爷爷与爸爸年龄之差.他们三人的年龄分别是多少?
任务一、认识三元一次方程组
x+y+z=120
z=x+y+12
y-x=z-y
这个问题的解必须同时满足上面三个方程,将这三个方程联立可得一个方程组.
探究新知
含有三个不同的未知数,每个方程中含有未知数的项的次数都是 1 ,像这样的方程组叫做三元一次方程组
含有三个未知数
未知数的项次数都是一次
特点
任务一、认识三元一次方程组
探究新知
x+y+z=120 ①
z=x+y+12 ②
y-x=z-y ③
思考:三元一次方程组必须有三个方程吗?每个方程必须是三元一次方程吗?
三元一次方程组并非必须有三个方程,也并非每个方程必须是三元一次方程
√
√
即学即练
判断下列方程组是不是三元一次方程组
x+2y+z=120
3x-y+z=2
2xy-x+z=6
x+y=7
9y+x=2
x+y=13
y+z=20
x+2y+z=120
3x-y+z=21
2y-x+z=7
三元一次方程组
一元一次方程
二元一次方程组
1.化“三元”为“二元”
消元
消元
三元一次方程组求法步骤:
2.化“二元”为“一元”
怎样解三元一次方程组?
(消去一个未知数)
任务二、解简单的三元一次方程组
探究新知
总结:
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
观察方程组:
考虑消去哪个未知数(也就是三个未知数要去掉哪一个 )
解法一:消去y
①+②,得 2x+2z=2
x+z=1 ④
x-z=4 ③
x+z=1 ④
解法二:消去x
2z+y=-2 ⑦
2z-y=-4 ⑧
(z+4)+y+z=2 ⑤
(z+4)-y+z=0 ⑥
化简得,
由③得,x=z+4 ④
把④代入①、②得,
解法三:消去z
把④代入①、②得
x+y+(x-4)=2 ⑤
x-y+(x-4)=0 ⑥
化简得,
由③得,z=x-4 ④
2x+y=6 ⑦
4-y= 0 ⑧
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
注:如果三个方程中有一个方程是二元一次方程(如例1中的③),则可以先对另外两个方程组进行消元,消元时就消去三个元中这个二元一次方程(如例1中的③)中缺少的那个元。缺某元,消某元。
在三元化二元时,对于具体方法的选取应该注意选择最恰当、最简便的方法。
解之,得
解: 由①+②,得
2x+2z=2,
化简,得
x+z=1 ④
由③+④,得
2x=5
x-z=4 ③
x+z= 1 ④
∴
把
代入②,得
解之,得 y=1
所以,原方程组的解是
解之,得
任务二、解简单的三元一次方程组
探究新知
x+y+z=2 ①
x-y+z=0 ②
x-z=4 ③
把 代入③,得
解:由③-②,得
典型例题
例2 解方程组
x+y=3 ①
y+z=5 ②
x+z=4 ③
x-y= -1 ④
由① + ④,得
解之,得
所以,原方程组的解是
把x=1代入方程①、③,分别得
x+y= 3 ①
x-y= -1 ④
联立①④得:
2x=2
x=1
y=2,z=3
x=1
y=2
z=3
在消去一个未知数得出比原方程组少一个未知数的二元一次方程组的过程中,原方程组的每一个方程一般都至少要用到一次.
例2 也可以这样解!
解:由①+②+③,得
即,
由⑤-①,得
由⑤-②,得
由⑤-③,得
典型例题
例2 解方程组
x+y=3 ①
y+z=5 ②
x+z=4 ③
2(x+y+z)= 12 ④
x+y+z= 6 ⑤
x=1
z=3
y=2
所以,原方程组的解是
x=1
y=2
z=3
课堂小结
(一)三元一次方程组的概念是什么
(二)解三元一次方程组的基本思路是什么
(三)在三元化二元时,对于具体方法的选取应该注意什么?
消元,把“三元”化为“一元”
含有三个不同的未知数,每个方程中含有未知数的项的次数都是 1 ,像这样的方程组叫做三元一次方程组
缺某元,消某元。
课后作业
作业:
P60练习 10.3
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
