2023-2024学年人教版七年级数学下册第5章 相交线与平行线 单元同步练习题(含解析)
文档属性
| 名称 | 2023-2024学年人教版七年级数学下册第5章 相交线与平行线 单元同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 457.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:53:33 | ||
图片预览

文档简介
2023-2024学年人教版七年级数学下册《第5章相交线与平行线》
单元同步练习题(附答案)
一、单选题
1.下列语句是命题的是( )
A.画一条直线 B.正数都大于零 C.多彩的青春 D.明天晴天吗?
2.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.内错角相等
3.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C. 比 D.曲
4.如图,小胡同学的家在点处,他在行走速度相同的情况下,想尽快地到达公路边,他选择沿线段去公路边,他这一选择用到的数学知识是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.垂线段最短 D.两点确定一条直线
5.如图,已知,,则( )
A. B. C. D.
6.如图,下列条件中,能判断的是( )
A. B.
C. D.
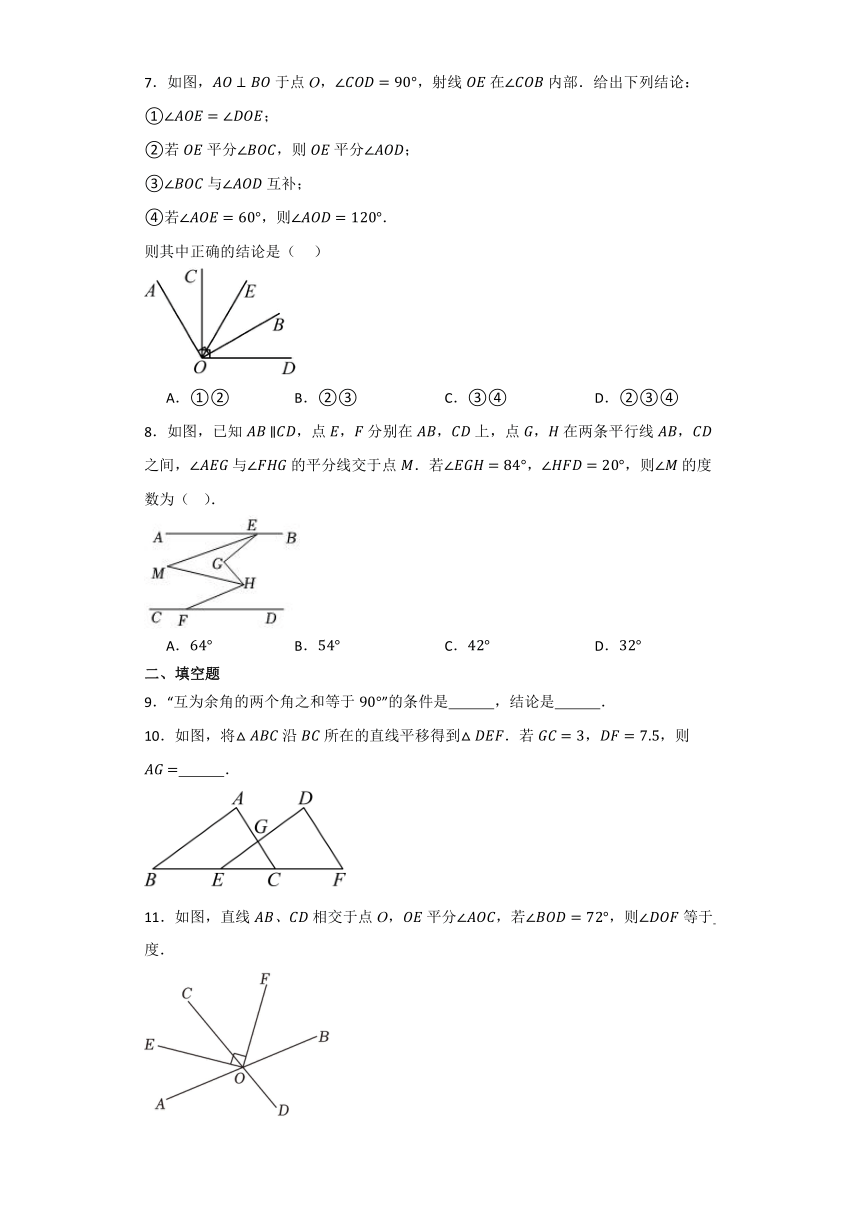
7.如图,于点O,,射线在内部.给出下列结论:
①;
②若平分,则平分;
③与互补;
④若,则.
则其中正确的结论是( )
A.①② B.②③ C.③④ D.②③④
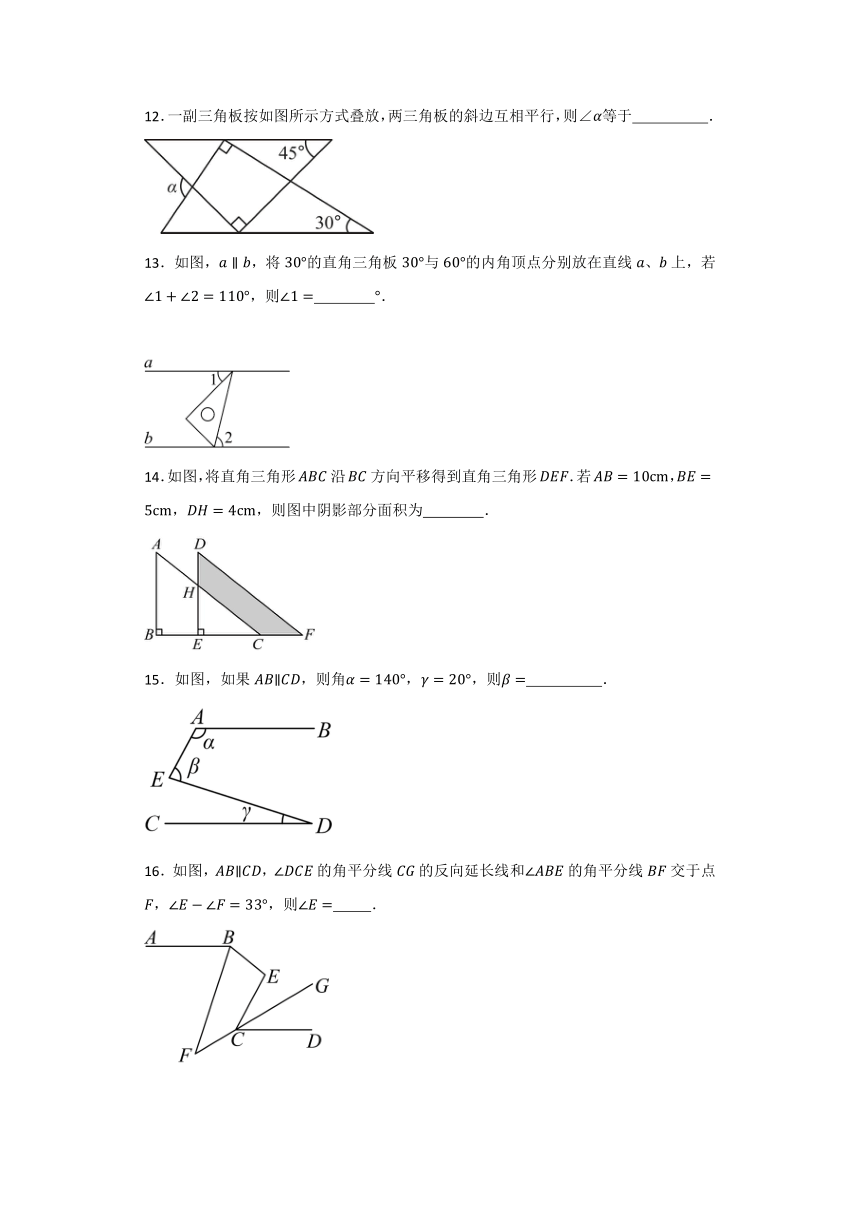
8.如图,已知 ,点,分别在,上,点,在两条平行线,之间,与的平分线交于点.若,,则的度数为( ).
A. B. C. D.
二、填空题
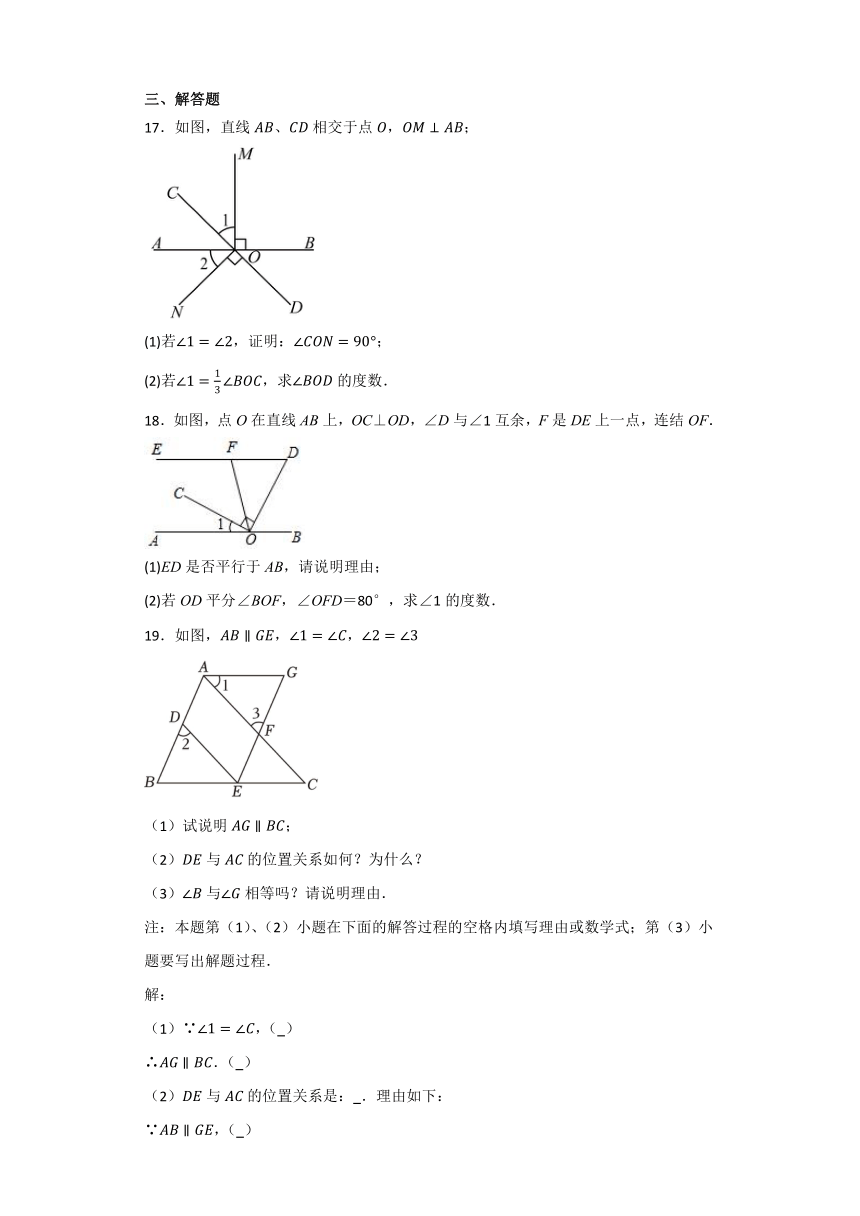
9.“互为余角的两个角之和等于”的条件是 ,结论是 .
10.如图,将沿所在的直线平移得到.若,,则 .
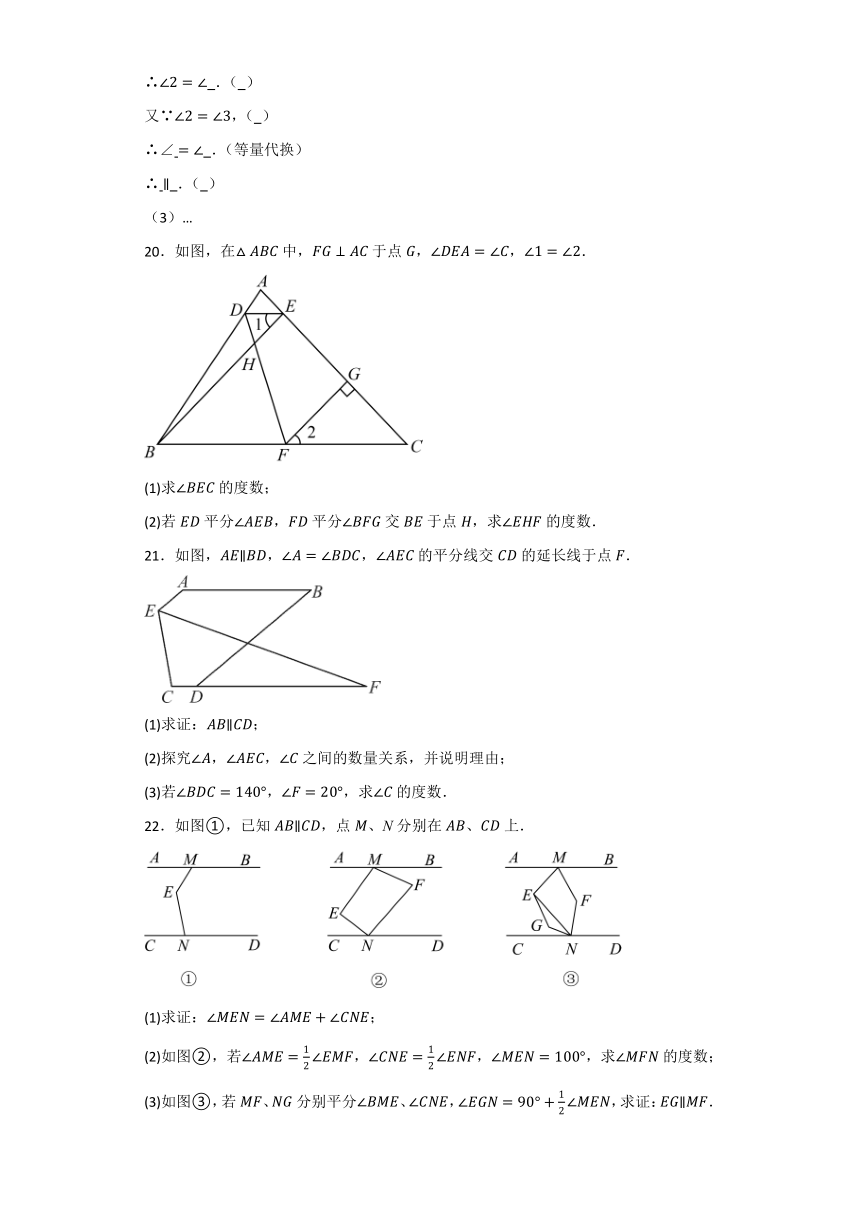
11.如图,直线相交于点O,平分,若,则等于 度.
12.一副三角板按如图所示方式叠放,两三角板的斜边互相平行,则∠等于 .
13.如图,,将的直角三角板与的内角顶点分别放在直线、上,若,则 .
14.如图,将直角三角形沿方向平移得到直角三角形.若,,,则图中阴影部分面积为 .
15.如图,如果,则角,,则 .
16.如图,,的角平分线的反向延长线和的角平分线交于点,,则 .
三、解答题
17.如图,直线、相交于点,;
(1)若,证明:;
(2)若,求的度数.
18.如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连结OF.
(1)ED是否平行于AB,请说明理由;
(2)若OD平分∠BOF,∠OFD=80°,求∠1的度数.
19.如图,,
(1)试说明;
(2)与的位置关系如何?为什么?
(3)与相等吗?请说明理由.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)∵,( )
∴.( )
(2)与的位置关系是: .理由如下:
∵,( )
∴ .( )
又∵,( )
∴∠ .(等量代换)
∴ .( )
(3)…
20.如图,在中,于点,,.
(1)求的度数;
(2)若平分,平分交于点,求的度数.
21.如图,,,的平分线交的延长线于点.
(1)求证:;
(2)探究,,之间的数量关系,并说明理由;
(3)若,,求的度数.
22.如图①,已知,点、N分别在、上.
(1)求证:;
(2)如图②,若,,,求的度数;
(3)如图③,若、分别平分、,,求证:.
参考答案
1.解:A、C、D中的语句不是命题,故A、C、D不符合题意;
B中的语句是命题,故B符合题意.
故选:B.
2.解:A. 两点之间,线段最短,是真命题,不符合题意;
B. 对顶角相等,是真命题,不符合题意;
C. 直角的补角仍然是直角,是真命题,不符合题意;
D. 内错角相等,是假命题,符合题意;
故选D.
3.解:由图可知A不是平移得到,B不是平移得到,D不是平移得到,
C是利用图形的平移得到.
故选:C.
4.解:小胡同学的家在点处,他在行走速度相同的情况下,想尽快地到达公路边,他选择沿线段去公路边,是因为垂线段最短;
故选: C
5.解:∵,,
∴,
∴;
故选C.
6.解:,
,
故A选项不符合题意;
,不能判定,
故B选项不符合题意;
,
,
故C选项符合题意;
,
,
故D选项不符合题意;
故选:C.
7.解:①由,无法确定,故①不正确;
②∵,,
∴,
∴.
∵平分,
∴,
∴,
∴,
∴平分,故②正确;
③∵
,
∴与互补,故③正确;
④∵无法确定,
∴若,则不一定等于,
∴不一定正确,故④不正确.
故选B.
8.解:如图所示,过点,,作,,,
.
,
.
,
,
,
,
,
,,
,
和是角平分线,
,
,
,
,
,,
,
即.
故选:D.
9.解:∵“互为余角的两个角之和等于90°”写成“如果…,那么…”形式为:如果两个角互为余角,那么这两个角的和等于,
∴“互为余角的两个角之和等于90°”的条件是两个角互为余角,结论是这两个角的和等于.
故答案为:两个角互为余角,这两个角的和等于.
10.解:由平移的性质可得:,
∴,
故答案为:.
11.解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
故答案为:.
12.解:过点E作,
如图,由题可知,,
又∵两三角板的斜边互相平行,
∴,
∴,
∴,
度答案为:.
13.解:∵,
∴,
∵,
∴,
∴,
故答案为:.
14.解:∵将直角三角形沿方向平移得到直角三角形,
∴,,
∵,
∴,
∴,
故答案为:.
15.解:过E作,
∵,
∴,
∴,,
∵,,
∴,,
∴,
故答案为:.
16.解:如图,过F作,
∵,
∴,
∵的角平分线的反向延长线和的角平分线交于点F,
∴可设,,
∴,,
∴四边形中,
,
即,①
又∵,
∴,②
∴,
解得,
故答案为:.
17.(1)证明:∵,
∴,
∴,
∵,
∴,
即;
(2)解:∵,
∴,
解得:,
∴.
18.(1)解:,理由如下:
∵∠D与∠1互余,
∴∠D+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠D+∠1+∠COD=180°,
∴∠D+∠AOD=180°,
∴;
(2)解:∵,
∴∠BOF+∠OFD=180°,
∵∠OFD=80°,
∴∠BOF=100°,
∵OD平分∠BOF,
∴,
∴∠1=180°-∠COD-∠BOD=180°-90°-50°=40°.
19.解:(1)∵,(已知 )
∴.(两直线平行,内错角相等)
故答案为:已知;两直线平行,内错角相等;
(2)与的位置关系是:平行.理由如下:
∵,(已知)
∴.(两直线平行,内错角相等)
又∵,(已知)
∴.(等量代换)
∴.(同位角相等,两直线平行)
故答案为:平行;已知;;两直线平行,内错角相等;已知;;3;;;同位角相等,两直线平行.
(3)与相等,理由如下:
∵,
∴,
由(1)可知:,
∴,
∴.
20.(1)解:∵∠DEA=∠C,
∴DE∥BC,
∴∠1=∠HBF,
∵∠1=∠2,
∴∠HBF=∠2,
∴BE∥GF,
∵FG⊥AC,
∴BE⊥AC,
∴∠BEC=90°;
(2)解:∵∠AEB=∠BEC=90°,DE平分∠AEB,
∴∠1=45°,即∠1=∠HBF=∠2=45°,
∴∠BFG=180°-∠2=135°,
∵FD平分∠BFG,
∴∠GFH=∠BFG=67.5°,
∵BE∥GF,
∴∠EHF+∠GFH=180°,
∴∠EHF=180°-∠GFH=180°-67.5°=112.5°.
21.(1)证明:,
,
,
,
;
(2)解:,
理由如下:
如图,作,
,
则,
由(1)可得,
,
,
,
,
;
(3)解:如图,作,
,
则,
,
,
由(1)可得,
,
,
,
的平分线交的延长线于点,
,
由(2)可得:,
.
22.解:(1)过点E作,
,
,
,
,
即:;
(2)
过F作,
,
,,
, ,
,
,
由(1)得,
,
(3)
、分别平分、,
,
,,
,
,
,
,
,
,
,
,
,
单元同步练习题(附答案)
一、单选题
1.下列语句是命题的是( )
A.画一条直线 B.正数都大于零 C.多彩的青春 D.明天晴天吗?
2.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.内错角相等
3.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C. 比 D.曲
4.如图,小胡同学的家在点处,他在行走速度相同的情况下,想尽快地到达公路边,他选择沿线段去公路边,他这一选择用到的数学知识是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.垂线段最短 D.两点确定一条直线
5.如图,已知,,则( )
A. B. C. D.
6.如图,下列条件中,能判断的是( )
A. B.
C. D.
7.如图,于点O,,射线在内部.给出下列结论:
①;
②若平分,则平分;
③与互补;
④若,则.
则其中正确的结论是( )
A.①② B.②③ C.③④ D.②③④
8.如图,已知 ,点,分别在,上,点,在两条平行线,之间,与的平分线交于点.若,,则的度数为( ).
A. B. C. D.
二、填空题
9.“互为余角的两个角之和等于”的条件是 ,结论是 .
10.如图,将沿所在的直线平移得到.若,,则 .
11.如图,直线相交于点O,平分,若,则等于 度.
12.一副三角板按如图所示方式叠放,两三角板的斜边互相平行,则∠等于 .
13.如图,,将的直角三角板与的内角顶点分别放在直线、上,若,则 .
14.如图,将直角三角形沿方向平移得到直角三角形.若,,,则图中阴影部分面积为 .
15.如图,如果,则角,,则 .
16.如图,,的角平分线的反向延长线和的角平分线交于点,,则 .
三、解答题
17.如图,直线、相交于点,;
(1)若,证明:;
(2)若,求的度数.
18.如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连结OF.
(1)ED是否平行于AB,请说明理由;
(2)若OD平分∠BOF,∠OFD=80°,求∠1的度数.
19.如图,,
(1)试说明;
(2)与的位置关系如何?为什么?
(3)与相等吗?请说明理由.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)∵,( )
∴.( )
(2)与的位置关系是: .理由如下:
∵,( )
∴ .( )
又∵,( )
∴∠ .(等量代换)
∴ .( )
(3)…
20.如图,在中,于点,,.
(1)求的度数;
(2)若平分,平分交于点,求的度数.
21.如图,,,的平分线交的延长线于点.
(1)求证:;
(2)探究,,之间的数量关系,并说明理由;
(3)若,,求的度数.
22.如图①,已知,点、N分别在、上.
(1)求证:;
(2)如图②,若,,,求的度数;
(3)如图③,若、分别平分、,,求证:.
参考答案
1.解:A、C、D中的语句不是命题,故A、C、D不符合题意;
B中的语句是命题,故B符合题意.
故选:B.
2.解:A. 两点之间,线段最短,是真命题,不符合题意;
B. 对顶角相等,是真命题,不符合题意;
C. 直角的补角仍然是直角,是真命题,不符合题意;
D. 内错角相等,是假命题,符合题意;
故选D.
3.解:由图可知A不是平移得到,B不是平移得到,D不是平移得到,
C是利用图形的平移得到.
故选:C.
4.解:小胡同学的家在点处,他在行走速度相同的情况下,想尽快地到达公路边,他选择沿线段去公路边,是因为垂线段最短;
故选: C
5.解:∵,,
∴,
∴;
故选C.
6.解:,
,
故A选项不符合题意;
,不能判定,
故B选项不符合题意;
,
,
故C选项符合题意;
,
,
故D选项不符合题意;
故选:C.
7.解:①由,无法确定,故①不正确;
②∵,,
∴,
∴.
∵平分,
∴,
∴,
∴,
∴平分,故②正确;
③∵
,
∴与互补,故③正确;
④∵无法确定,
∴若,则不一定等于,
∴不一定正确,故④不正确.
故选B.
8.解:如图所示,过点,,作,,,
.
,
.
,
,
,
,
,
,,
,
和是角平分线,
,
,
,
,
,,
,
即.
故选:D.
9.解:∵“互为余角的两个角之和等于90°”写成“如果…,那么…”形式为:如果两个角互为余角,那么这两个角的和等于,
∴“互为余角的两个角之和等于90°”的条件是两个角互为余角,结论是这两个角的和等于.
故答案为:两个角互为余角,这两个角的和等于.
10.解:由平移的性质可得:,
∴,
故答案为:.
11.解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
故答案为:.
12.解:过点E作,
如图,由题可知,,
又∵两三角板的斜边互相平行,
∴,
∴,
∴,
度答案为:.
13.解:∵,
∴,
∵,
∴,
∴,
故答案为:.
14.解:∵将直角三角形沿方向平移得到直角三角形,
∴,,
∵,
∴,
∴,
故答案为:.
15.解:过E作,
∵,
∴,
∴,,
∵,,
∴,,
∴,
故答案为:.
16.解:如图,过F作,
∵,
∴,
∵的角平分线的反向延长线和的角平分线交于点F,
∴可设,,
∴,,
∴四边形中,
,
即,①
又∵,
∴,②
∴,
解得,
故答案为:.
17.(1)证明:∵,
∴,
∴,
∵,
∴,
即;
(2)解:∵,
∴,
解得:,
∴.
18.(1)解:,理由如下:
∵∠D与∠1互余,
∴∠D+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠D+∠1+∠COD=180°,
∴∠D+∠AOD=180°,
∴;
(2)解:∵,
∴∠BOF+∠OFD=180°,
∵∠OFD=80°,
∴∠BOF=100°,
∵OD平分∠BOF,
∴,
∴∠1=180°-∠COD-∠BOD=180°-90°-50°=40°.
19.解:(1)∵,(已知 )
∴.(两直线平行,内错角相等)
故答案为:已知;两直线平行,内错角相等;
(2)与的位置关系是:平行.理由如下:
∵,(已知)
∴.(两直线平行,内错角相等)
又∵,(已知)
∴.(等量代换)
∴.(同位角相等,两直线平行)
故答案为:平行;已知;;两直线平行,内错角相等;已知;;3;;;同位角相等,两直线平行.
(3)与相等,理由如下:
∵,
∴,
由(1)可知:,
∴,
∴.
20.(1)解:∵∠DEA=∠C,
∴DE∥BC,
∴∠1=∠HBF,
∵∠1=∠2,
∴∠HBF=∠2,
∴BE∥GF,
∵FG⊥AC,
∴BE⊥AC,
∴∠BEC=90°;
(2)解:∵∠AEB=∠BEC=90°,DE平分∠AEB,
∴∠1=45°,即∠1=∠HBF=∠2=45°,
∴∠BFG=180°-∠2=135°,
∵FD平分∠BFG,
∴∠GFH=∠BFG=67.5°,
∵BE∥GF,
∴∠EHF+∠GFH=180°,
∴∠EHF=180°-∠GFH=180°-67.5°=112.5°.
21.(1)证明:,
,
,
,
;
(2)解:,
理由如下:
如图,作,
,
则,
由(1)可得,
,
,
,
,
;
(3)解:如图,作,
,
则,
,
,
由(1)可得,
,
,
,
的平分线交的延长线于点,
,
由(2)可得:,
.
22.解:(1)过点E作,
,
,
,
,
即:;
(2)
过F作,
,
,,
, ,
,
,
由(1)得,
,
(3)
、分别平分、,
,
,,
,
,
,
,
,
,
,
,
,
