鲁教版八年级数学下册第3章3.1平均数同步测试题(含答案)
文档属性
| 名称 | 鲁教版八年级数学下册第3章3.1平均数同步测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 65.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-17 21:09:25 | ||
图片预览


文档简介
鲁教版八年级数学下册第3章3.1平均数同步测试题(含答案)
一.选择题(共10小题)
1.(2015 呼和浩特一模)已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B. 5 C. 4 D. 2
2.(2015 清远模拟)已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B. +3 C. +10 D. +12
3.(2015 徐州校级模拟)某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资各不相同.若该单位员工的月平均工资是1500元,则下列说法中正确的是( )
A. 所有员工的月工资都是1500元
B. 一定有一名员工的月工资是1500元
C. 至少有一名员工的月工资高于1500元
D. 一定有一半员工的月工资高于1500元
4.(2015 玉林)学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B. 2.8 C. 3 D. 3.3
(4题图) (6题图)
5.(2015 恩施州一模)将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B. 36 C. 37 D. 38
6.(2015 武汉模拟)在一次捐款活动中,某班50名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的,如图所示的统计图反映了不同捐款数的人数比例,那么根据图中信息,该班同学平均每人捐款( )
A.30元 B. 33元 C. 36元 D. 35元
7.(2015 河南)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B. 84分 C. 84.5分 D. 86分
8.(2015 西安模拟)在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示:这8名同学捐款的平均金额约为( )
金额/元 5 6 7 10
人数 2 3 2 1
A.6.5元 B. 6元 C. 3.5元 D. 7元
9.某商店5天的营业额如下(单位:元):14845,25706,18957,11672,16330,利用计算器求得这5天的平均营业额是( )
A.18116元 B. 17805元 C. 17502元 D. 16678元
10.用计算器求一组数据21,22,25,23,27,19,24,20,25,24,18,27的平均数是(保留一位小数)( )
A.22.7 B. 22.8 C. 22.9 D. 23.0
二.填空题(共10小题)
11.(2015 武汉)一组数据2,3,6,8,11的平均数是 .
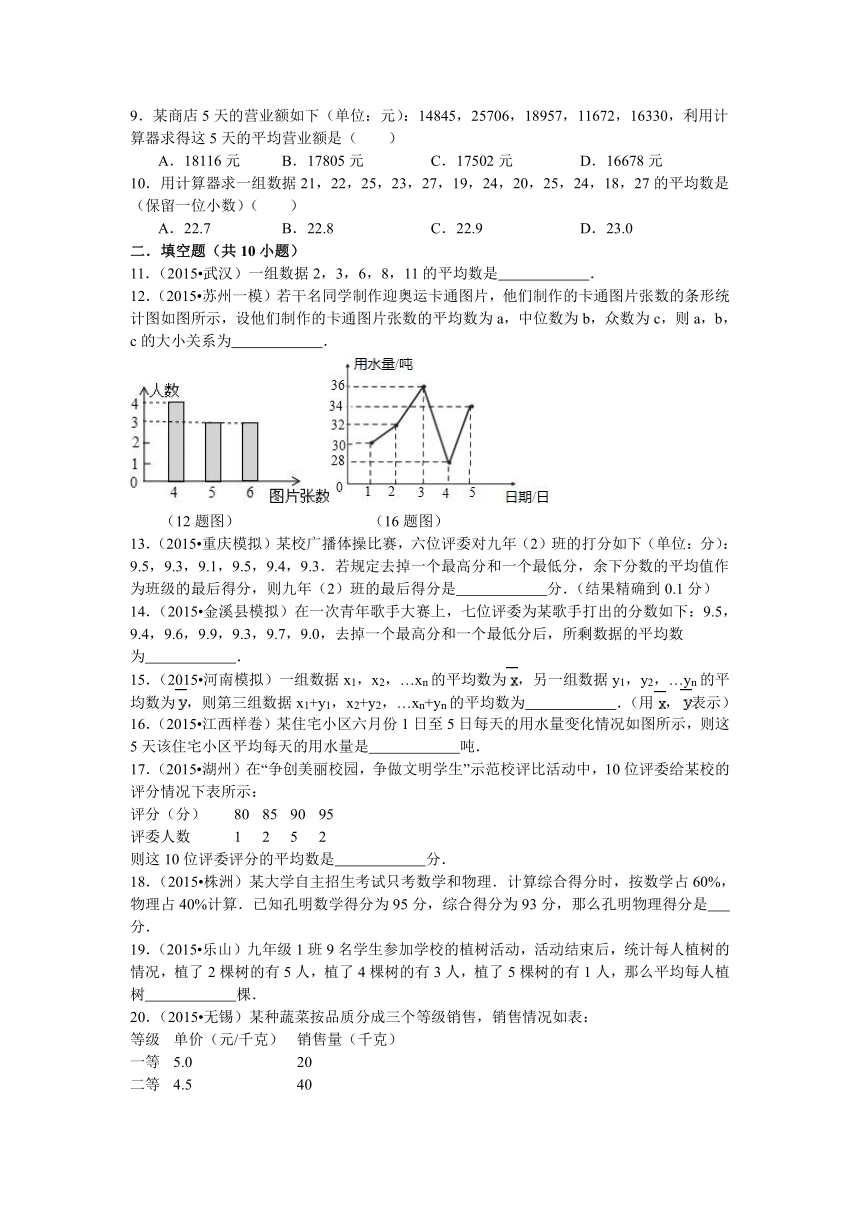
12.(2015 苏州一模)若干名同学制作迎奥运卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为 .
(12题图) (16题图)
13.(2015 重庆模拟)某校广播体操比赛,六位评委对九年(2)班的打分如下(单位:分):9.5,9.3,9.1,9.5,9.4,9.3.若规定去掉一个最高分和一个最低分,余下分数的平均值作为班级的最后得分,则九年(2)班的最后得分是 分.(结果精确到0.1分)
14.(2015 金溪县模拟)在一次青年歌手大赛上,七位评委为某歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数为 .
15.(2015 河南模拟)一组数据x1,x2,…xn的平均数为,另一组数据y1,y2,…yn的平均数为,则第三组数据x1+y1,x2+y2,…xn+yn的平均数为 .(用,表示)
16.(2015 江西样卷)某住宅小区六月份1日至5日每天的用水量变化情况如图所示,则这5天该住宅小区平均每天的用水量是 吨.
17.(2015 湖州)在“争创美丽校园,争做文明学生”示范校评比活动中,10位评委给某校的评分情况下表所示:
评分(分) 80 85 90 95
评委人数 1 2 5 2
则这10位评委评分的平均数是 分.
18.(2015 株洲)某大学自主招生考试只考数学和物理.计算综合得分时,按数学占60%,物理占40%计算.已知孔明数学得分为95分,综合得分为93分,那么孔明物理得分是 分.
19.(2015 乐山)九年级1班9名学生参加学校的植树活动,活动结束后,统计每人植树的情况,植了2棵树的有5人,植了4棵树的有3人,植了5棵树的有1人,那么平均每人植树 棵.
20.(2015 无锡)某种蔬菜按品质分成三个等级销售,销售情况如表:
等级 单价(元/千克) 销售量(千克)
一等 5.0 20
二等 4.5 40
三等 4.0 40
则售出蔬菜的平均单价为 元/千克.
三.解答题(共6小题)
21.(2014 甘肃模拟)计算数据5,9,8,10,3的平均数.
22.(2014秋 朝阳区期末)下表是某班5名同学某次数学测试成绩.根据信息完成下表,并回答问题.五人中分数最高的是谁?分数最低的是谁?谁的分数与全班平均分最接近?
姓名 王芳 刘兵 张昕 李聪 江文
成绩 89 84
与全班平均分之差 ﹣1 +2 0 ﹣2
23.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
24.(2015 温州)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 面试 体能
甲 83 79 90
乙 85 80 75
丙 80 90 73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
25.(2015 甘孜州)某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 75 80 90
面试 93 70 68
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
26.(2015 梧州)某企业招聘员工,要求所要应聘者都要经过笔试与面试两种考核,且按考核总成绩从高到低进行录取,如果考核总成绩相同时,则优先录取面试成绩高分者.下面是招聘考和总成绩的计算说明:
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
应聘者 成绩
笔试成绩 加分 面试成绩
甲 117 3 85.6
乙 121 0 85.1
(1)甲、乙两人面试的平均成绩为 ;
(2)甲应聘者的考核总成绩为 ;
(3)根据上表的数据,若只应聘1人,则应录取 .
鲁教版八年级数学下册第3章3.1平均数同步测试题参考答案
一.选择题(共10小题)
1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.A 9.C 10.C
二.填空题(共10小题)
11.6 12.b>a>c 13.9.4 14.9.5 15.+ 16.32
17.89 18.90 19.3 20.4.4
三.解答题(共6小题)
21.解:数据5,9,8,10,3的平均数是:(5+9+8+10+3)÷5=7.
22. 解:完成表格得
姓名 王芳 刘兵 张昕 李聪 江文
成绩 89 92 90 84 88
与全班平均分之差 ﹣1 +2 0 ﹣6 ﹣2
故答案为分数最高的是刘兵,分数最低的是李聪,张昕的分数与全班平均分最接近.
23.解:设一组数据x1,x2,…,xn的平均数是m,
即=,
则x1+x2+…+xn=mn.
(1)∵x1+x2+…+xn=mn,
∴x1+3+x2+3+…+xn+3=mn+3n,
∴x1+3,x2+3,…,xn+3的平均数是=m+3;
(2)∵x1+x2+…+xn=mn,
∴2x1+2x2+…+2xn=2mn,
∴2x1,2x2,…,2xn的平均数是=2m.
24.解:(1)甲=(83+79+90)÷3=84,
乙=(85+80+75)÷3=80,
丙=(80+90+73)÷3=81.
从高到低确定三名应聘者的排名顺序为:甲,丙,乙;
(2)∵该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,
∴甲淘汰;
乙成绩=85×60%+80×30%+75×10%=82.5,
丙成绩=80×60%+90×30%+73×10%=82.3,
25.解:(1)甲民主评议的得分是:
200×25%=50(分);
乙民主评议的得分是:
200×40%=80(分);
丙民主评议的得分是:
200×35%=70(分).
(2)甲的成绩是:
(75×4+93×3+50×3)÷(4+3+3)
=729÷10
=72.9(分)
乙的成绩是:
(80×4+70×3+80×3)÷(4+3+3)
=770÷10
=77(分)
丙的成绩是:
(90×4+68×3+70×3)÷(4+3+3)
=774÷10
=77.4(分)
∵77.4>77>72.9,
∴丙的得分最高.
26.解:(1)∵甲的面试成绩为85.6分,乙的面试成绩为85.1分,
∴甲、乙两人面试的平均成绩==85.35(分).
故答案为:85.35;
(2)∵甲的笔试总成绩=(117+3)÷2=60分,面试成绩=85.6分,
∴甲应聘者的考核总成绩=60+85.6=145.6(分).
故答案为:145.6;
(3)∵乙的笔试总成绩=121÷2=59.5分,面试成绩=85.1分,
∴甲应聘者的考核总成绩=59.5+85.1=144.6(分)<145.6分
∴应录取甲.
故答案为:甲.
一.选择题(共10小题)
1.(2015 呼和浩特一模)已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B. 5 C. 4 D. 2
2.(2015 清远模拟)已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B. +3 C. +10 D. +12
3.(2015 徐州校级模拟)某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资各不相同.若该单位员工的月平均工资是1500元,则下列说法中正确的是( )
A. 所有员工的月工资都是1500元
B. 一定有一名员工的月工资是1500元
C. 至少有一名员工的月工资高于1500元
D. 一定有一半员工的月工资高于1500元
4.(2015 玉林)学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B. 2.8 C. 3 D. 3.3
(4题图) (6题图)
5.(2015 恩施州一模)将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B. 36 C. 37 D. 38
6.(2015 武汉模拟)在一次捐款活动中,某班50名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的,如图所示的统计图反映了不同捐款数的人数比例,那么根据图中信息,该班同学平均每人捐款( )
A.30元 B. 33元 C. 36元 D. 35元
7.(2015 河南)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B. 84分 C. 84.5分 D. 86分
8.(2015 西安模拟)在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示:这8名同学捐款的平均金额约为( )
金额/元 5 6 7 10
人数 2 3 2 1
A.6.5元 B. 6元 C. 3.5元 D. 7元
9.某商店5天的营业额如下(单位:元):14845,25706,18957,11672,16330,利用计算器求得这5天的平均营业额是( )
A.18116元 B. 17805元 C. 17502元 D. 16678元
10.用计算器求一组数据21,22,25,23,27,19,24,20,25,24,18,27的平均数是(保留一位小数)( )
A.22.7 B. 22.8 C. 22.9 D. 23.0
二.填空题(共10小题)
11.(2015 武汉)一组数据2,3,6,8,11的平均数是 .
12.(2015 苏州一模)若干名同学制作迎奥运卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为 .
(12题图) (16题图)
13.(2015 重庆模拟)某校广播体操比赛,六位评委对九年(2)班的打分如下(单位:分):9.5,9.3,9.1,9.5,9.4,9.3.若规定去掉一个最高分和一个最低分,余下分数的平均值作为班级的最后得分,则九年(2)班的最后得分是 分.(结果精确到0.1分)
14.(2015 金溪县模拟)在一次青年歌手大赛上,七位评委为某歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数为 .
15.(2015 河南模拟)一组数据x1,x2,…xn的平均数为,另一组数据y1,y2,…yn的平均数为,则第三组数据x1+y1,x2+y2,…xn+yn的平均数为 .(用,表示)
16.(2015 江西样卷)某住宅小区六月份1日至5日每天的用水量变化情况如图所示,则这5天该住宅小区平均每天的用水量是 吨.
17.(2015 湖州)在“争创美丽校园,争做文明学生”示范校评比活动中,10位评委给某校的评分情况下表所示:
评分(分) 80 85 90 95
评委人数 1 2 5 2
则这10位评委评分的平均数是 分.
18.(2015 株洲)某大学自主招生考试只考数学和物理.计算综合得分时,按数学占60%,物理占40%计算.已知孔明数学得分为95分,综合得分为93分,那么孔明物理得分是 分.
19.(2015 乐山)九年级1班9名学生参加学校的植树活动,活动结束后,统计每人植树的情况,植了2棵树的有5人,植了4棵树的有3人,植了5棵树的有1人,那么平均每人植树 棵.
20.(2015 无锡)某种蔬菜按品质分成三个等级销售,销售情况如表:
等级 单价(元/千克) 销售量(千克)
一等 5.0 20
二等 4.5 40
三等 4.0 40
则售出蔬菜的平均单价为 元/千克.
三.解答题(共6小题)
21.(2014 甘肃模拟)计算数据5,9,8,10,3的平均数.
22.(2014秋 朝阳区期末)下表是某班5名同学某次数学测试成绩.根据信息完成下表,并回答问题.五人中分数最高的是谁?分数最低的是谁?谁的分数与全班平均分最接近?
姓名 王芳 刘兵 张昕 李聪 江文
成绩 89 84
与全班平均分之差 ﹣1 +2 0 ﹣2
23.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
24.(2015 温州)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 面试 体能
甲 83 79 90
乙 85 80 75
丙 80 90 73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
25.(2015 甘孜州)某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 75 80 90
面试 93 70 68
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
26.(2015 梧州)某企业招聘员工,要求所要应聘者都要经过笔试与面试两种考核,且按考核总成绩从高到低进行录取,如果考核总成绩相同时,则优先录取面试成绩高分者.下面是招聘考和总成绩的计算说明:
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
应聘者 成绩
笔试成绩 加分 面试成绩
甲 117 3 85.6
乙 121 0 85.1
(1)甲、乙两人面试的平均成绩为 ;
(2)甲应聘者的考核总成绩为 ;
(3)根据上表的数据,若只应聘1人,则应录取 .
鲁教版八年级数学下册第3章3.1平均数同步测试题参考答案
一.选择题(共10小题)
1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.A 9.C 10.C
二.填空题(共10小题)
11.6 12.b>a>c 13.9.4 14.9.5 15.+ 16.32
17.89 18.90 19.3 20.4.4
三.解答题(共6小题)
21.解:数据5,9,8,10,3的平均数是:(5+9+8+10+3)÷5=7.
22. 解:完成表格得
姓名 王芳 刘兵 张昕 李聪 江文
成绩 89 92 90 84 88
与全班平均分之差 ﹣1 +2 0 ﹣6 ﹣2
故答案为分数最高的是刘兵,分数最低的是李聪,张昕的分数与全班平均分最接近.
23.解:设一组数据x1,x2,…,xn的平均数是m,
即=,
则x1+x2+…+xn=mn.
(1)∵x1+x2+…+xn=mn,
∴x1+3+x2+3+…+xn+3=mn+3n,
∴x1+3,x2+3,…,xn+3的平均数是=m+3;
(2)∵x1+x2+…+xn=mn,
∴2x1+2x2+…+2xn=2mn,
∴2x1,2x2,…,2xn的平均数是=2m.
24.解:(1)甲=(83+79+90)÷3=84,
乙=(85+80+75)÷3=80,
丙=(80+90+73)÷3=81.
从高到低确定三名应聘者的排名顺序为:甲,丙,乙;
(2)∵该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,
∴甲淘汰;
乙成绩=85×60%+80×30%+75×10%=82.5,
丙成绩=80×60%+90×30%+73×10%=82.3,
25.解:(1)甲民主评议的得分是:
200×25%=50(分);
乙民主评议的得分是:
200×40%=80(分);
丙民主评议的得分是:
200×35%=70(分).
(2)甲的成绩是:
(75×4+93×3+50×3)÷(4+3+3)
=729÷10
=72.9(分)
乙的成绩是:
(80×4+70×3+80×3)÷(4+3+3)
=770÷10
=77(分)
丙的成绩是:
(90×4+68×3+70×3)÷(4+3+3)
=774÷10
=77.4(分)
∵77.4>77>72.9,
∴丙的得分最高.
26.解:(1)∵甲的面试成绩为85.6分,乙的面试成绩为85.1分,
∴甲、乙两人面试的平均成绩==85.35(分).
故答案为:85.35;
(2)∵甲的笔试总成绩=(117+3)÷2=60分,面试成绩=85.6分,
∴甲应聘者的考核总成绩=60+85.6=145.6(分).
故答案为:145.6;
(3)∵乙的笔试总成绩=121÷2=59.5分,面试成绩=85.1分,
∴甲应聘者的考核总成绩=59.5+85.1=144.6(分)<145.6分
∴应录取甲.
故答案为:甲.
