北师大版六年级下册第二单元比例解决问题专项突破三(含答案)
文档属性
| 名称 | 北师大版六年级下册第二单元比例解决问题专项突破三(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 727.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 21:19:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版六年级下册第二单元比例解决问题专项突破三
一、解答题
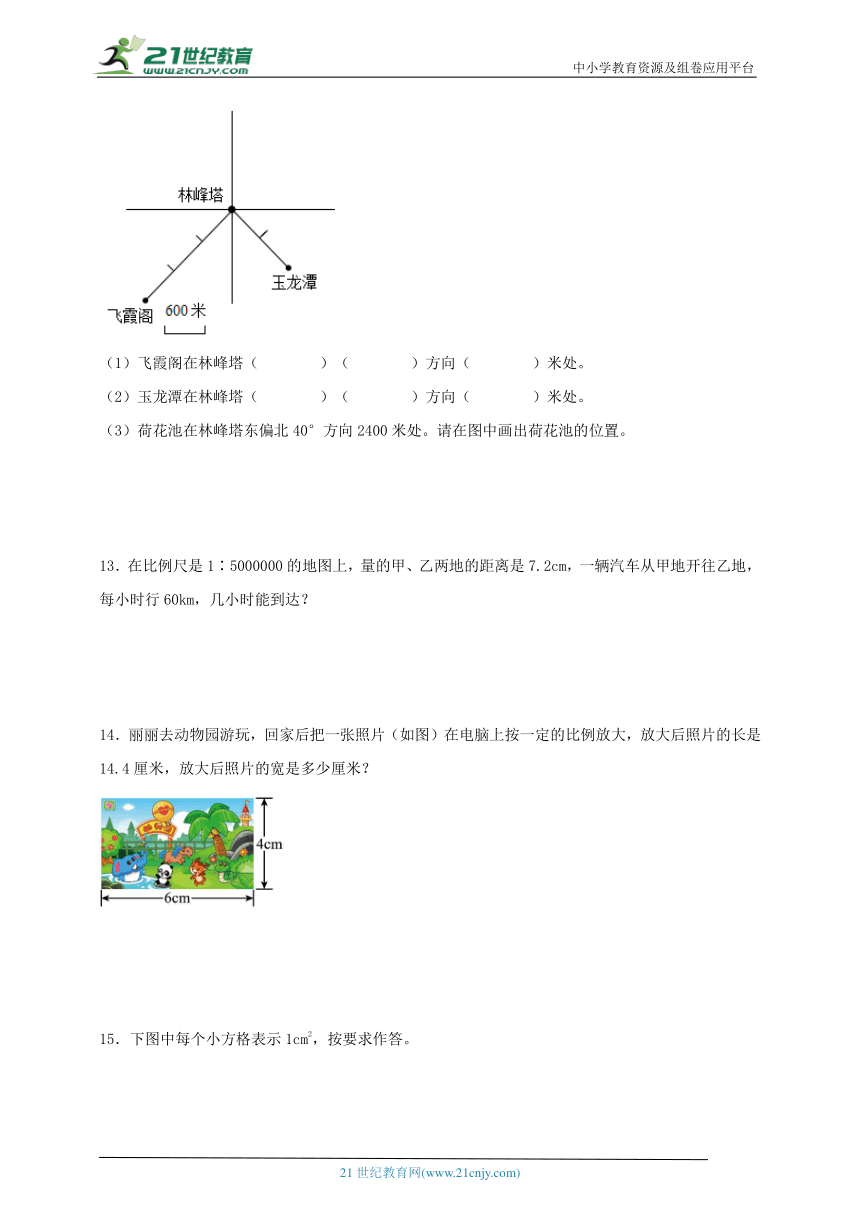
1.按要求完成下面各题。
(1)以学校为观测点,文化宫在学校的( )偏( )( )°方向( )km处;体育馆在学校的( )偏( )( )°方向( )km处。
(2)图书馆在学校南偏西45°方向2km处,公园在学校东偏北20°方向3km处。在图中标出图书馆和公园的位置。
2.在比例尺为1∶1000000的地图上,量得甲,乙两地的距离为8厘米,一辆汽车以每小时80千米的速度从甲地出发开往乙地,经过几小时可以到达乙地?
3.按要求填空。(测量图上距高时取整厘米)
(1)学校到街心花园的实际距为900米,这幅图的比例尺是( )。
(2)足球场在街心花园的( )偏( )°方向( )米处。
(3)游泳馆在街心花园南偏西30°方向600米处,请在图中用“Y”标出它的位置。
4.在比例尺是1∶7500000的地图上,量得甲、乙两地相距12厘米,一辆汽车以每小时60千米的速度从甲地开往乙地,需要多少小时能走完全程?
5.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
6.学校食堂运来30袋大米,每袋,第1周(5天)用了照这样计算,这批大米能用多少天?(列比例解答)
7.小明一家人从甲城出发去丙城旅游,途中要经过乙城,如图所示,他们全程共行驶了多少千米?(测量结果取整厘米数)
8.一块长方形地长和宽的比是7∶4,将其画在比例尺为1∶1000的图纸上,所得图形的周长是44厘米。这块地的实际面积是多少平方米?
9.在一幅比例尺是1∶300000的地图上,量得A、B两地的距离是15厘米,请你计算出A、B两地之间的实际距离是多少千米?
10.在标有的地图上,量得南京到上海的距离为8厘米。暑假期间家住南京的李磊同学全家开车前往上海,早上6:00出发,到达第一个收费站时已经行了160千米,李磊的爸爸看了看手表,此时刚好是8:00,照这样的速度,他们9:50能到达上海吗?
11.科技的发展改善了我们的生活,也改变了人们的出行方式,人们可以选择的交通工具多种多样,如:地铁、汽车、高铁、火车、飞机等。据了解,从济南到郑州的公路长是440km。若一辆车2小时行了160km,照这样计算,从济南到郑州需要多少个小时?先说说路程和时间成什么比例,再用比例解。
12.下图是南山风景区的平面图。
(1)飞霞阁在林峰塔( )( )方向( )米处。
(2)玉龙潭在林峰塔( )( )方向( )米处。
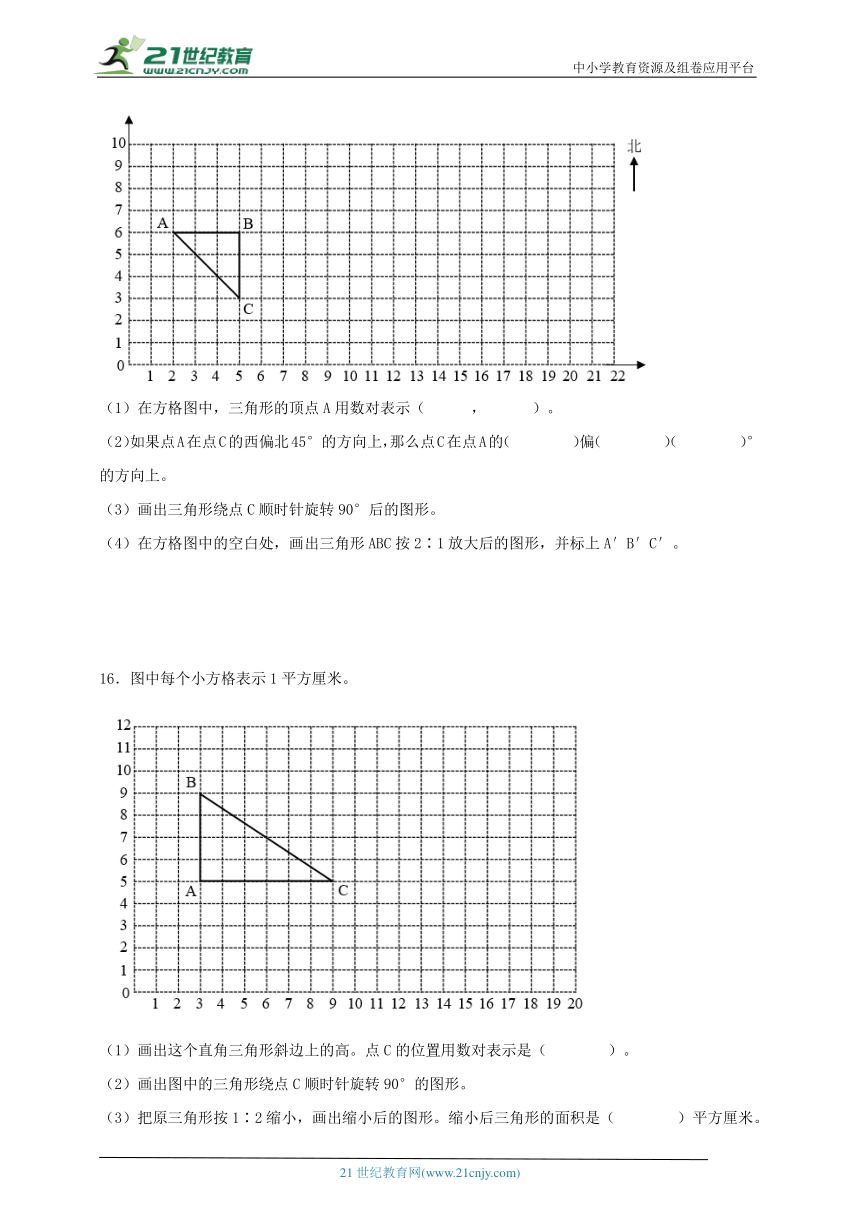
(3)荷花池在林峰塔东偏北40°方向2400米处。请在图中画出荷花池的位置。
13.在比例尺是1∶5000000的地图上,量的甲、乙两地的距离是7.2cm,一辆汽车从甲地开往乙地,每小时行60km,几小时能到达?
14.丽丽去动物园游玩,回家后把一张照片(如图)在电脑上按一定的比例放大,放大后照片的长是14.4厘米,放大后照片的宽是多少厘米?
15.下图中每个小方格表示1cm2,按要求作答。
(1)在方格图中,三角形的顶点A用数对表示( , )。
(2)如果点A在点C的西偏北45°的方向上,那么点C在点A的( )偏( )( )°的方向上。
(3)画出三角形绕点C顺时针旋转90°后的图形。
(4)在方格图中的空白处,画出三角形ABC按2∶1放大后的图形,并标上A′B′C′。
16.图中每个小方格表示1平方厘米。
(1)画出这个直角三角形斜边上的高。点C的位置用数对表示是( )。
(2)画出图中的三角形绕点C顺时针旋转90°的图形。
(3)把原三角形按1∶2缩小,画出缩小后的图形。缩小后三角形的面积是( )平方厘米。
17.(1)图中点A的位置用数对( )表示,点B的位置用数对( )表示。
(2)图中每个小正方形的面积表示1平方厘米,请以AB为一条边,画一个面积是6平方厘米的三角形ABC。
(3)将三角形ABC按2∶1放大后画在方格纸上。
18.货车运一批货物,4天运了36吨。照这样的效率,再运3天就能运完。这批货物共有多少吨?(用比例解)
19.一辆货车前往武汉灾区运送救灾物资,3小时行驶了45千米。从出发地到灾区150千米,按照这样的速度,全程需要多少小时?(列比例解答)
20.2020年我国正式进入5G时代。目前5G正以更快的速度、更稳定的连接与更大的容量融入各行各业。小明原来用4G下载电影《流浪地球》需要8分钟,而他现在用5G下载这部电影所用的时间与用4G下载所用时间的比是1∶100。那么他用5G下载这部电影要用多少秒?(用比例解)
21.防疫时期,教室地面和桌子表面需要消毒。桶里放有6.4升水,根据说明,需加入多少消毒剂?(用比例解答)
22.某工程队修一条路,15天共修900米,还剩下720米没有修。照这样的速度,修完这条公路共需要多少天?(尝试用比例的方法解,可得6分,其它方法解得5分)
23.在一幅比例尺为1∶5000000的地图上,量得A、B两地间公路全长是12厘米。一辆客车和一辆货车同时从A、B两地相对开出,5小时后相遇。已知客车和货车的速度比是3∶2,货车的速度是多少千米/时?
24.兄弟两人月收入的比为4∶3,月支出比为11∶6,月结余均为3600元,问每人每月收入多少元?
25.一列火车通过一座长2000米的大桥要60秒,如果用同样的速度通过一座1460米的隧道则要45秒,这列火车长多少米?(利用比例知识解答)
参考答案
1.(1)西;北;30;3,南;东;40;2
(2)见详解
【分析】(1)地图上的方位是“上北下南,左西右东”,比例尺是图上1厘米表示实际1千米,利用比例尺和图上距离,得出实际距离,据此解答;
(2)根据比例尺和实际距离可计算出图上距离,图书馆距离学校2厘米,公园距离学校3厘米,再结合所给的角度及图上确定方向的方法确定图书馆和公园的位置,并作图即可。
【详解】(1) 以学校为观测点,文化宫在学校的西偏北30°方向3km处;体育馆在学校的南偏东40°方向2km处。
(2)
【点睛】掌握地图的方位及比例尺的意义是解答本题的关键。
2.1小时
【分析】已知比例尺和图上距离求实际距离,依据“实际距离=图上距离÷比例尺”即可求出实际距离,再根据路程÷速度=时间,列式解答。
【详解】8÷
=8×1000000
=8000000(厘米)
=80(千米)
80÷80=1(小时)
答:经过1小时可以到达。
【点睛】此题主要考查比例尺的意义及已知比例尺和图上距离求实际距离,注意单位的换算。
3.(1)1∶30000
(2)东,北60;1200
(3)见详解
【分析】(1)用尺子测量,即可知道学校到街心花园的距离是3厘米,实际距离是900米,根据比例尺的公式:比例尺=图上距离∶实际距离,把数代入公式即可求解,要注意统一单位。
(2)根据地图上的方向(上北下南,左西右东),即可找出足球场在街心花园的方向,之后量出街心花园到足球场的图上距离,再根据公式:实际距离=图上距离÷比例尺,求出实际距离。
(3)图上距离=实际距离×比例尺,求出图上距离,再根据地图上的方向(上北下南,左西右东),即可找出游泳馆的位置。
【详解】(1)900米=90000厘米
3厘米∶90000厘米
=(3÷3)∶(90000÷3)
=1∶30000
所以这幅图的比例尺是:1∶30000
(2)足球场在街心花园图上距离4厘米处
4×30000=120000(厘米)
120000厘米=1200米
即足球场在街心花园的北偏东60°方向1200米。
(3)600米=60000厘米
60000×=2(厘米)
如下图所示:
【点睛】本题主要学会找准方向,并熟练掌握图上距离和实际距离的关系是解题的关键。
4.15小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,即可解答。
【详解】12÷
=12×7500000
=90000000(厘米)
90000000厘米=900千米
900÷60=15(小时)
答:需要15小时能走完全程。
【点睛】本题考查实际距离和图上距离的换算,以及利用速度、时间和距离三者关系进行解答,注意单位名数的换算。
5.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
【点睛】本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
6.15天
【分析】根据题意可知,每天用大米的质量是一定的,每天用大米的质量=总质量÷天数,据此列比例解答。
【详解】解:设这批大米能用x天。
400x=6000
x=15
答:这批大米能用15天。
【点睛】此题考查了比例的实际应用,找出相关的量是比值一定还是乘积一定是解题关键。
7.600千米
【分析】先量出从甲城出发途经乙城去丙城的图上距离,再根据比例尺求出实际距离,解答即可。
【详解】如图:
量出从甲城出发途经乙城去丙城的图上距离是1+2=3(厘米)
3×20000000=60000000(厘米)
60000000厘米=600千米
答:全程共行驶600千米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
8.11200平方米
【分析】依据长方形的周长公式求出长方形的长与宽的和,长与宽的比是7∶4,根据按比分配的方法求出长方形的长和宽的图上长度;再依据“实际距离=图上距离÷比例尺”即可求出这块地的长和宽的实际长度,从而利用长方形的面积公式求出实际面积。
【详解】44÷2=22(厘米)
22×
=22×
=14(厘米)
22×
=22×
=8(厘米)
14÷=14×1000=14000(厘米)=140(米)
8×=8×1000=8000(厘米)=80(米)
140×80=11200(平方米)
答:这块地的实际面积是11200平方米。
【点睛】此题主要考查长方形的周长和面积的计算方法在实际生活中的应用以及图上距离、实际距离和比例尺的关系。
9.45千米
【分析】根据实际距离=图上距离÷比例尺,代入数据计算即可;注意单位的换算:1千米=100000厘米。
【详解】15÷=4500000(厘米)
4500000厘米=45千米
答:A、B两地之间的实际距离是45千米。
【点睛】掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
10.不能,行驶全程要4小时,要10:00到达
【分析】根据比例尺可知图上1厘米表示实际距离40千米,所以用40×8可求出南京到上海的实际距离,又知2小时行了160千米,所以可求出汽车的速度,用南京到上海的实际距离除以汽车的速度就是行完全程所以需要的时间,再与计划时间比较得解。
【详解】40×8=320(千米)
160÷(8-6)
=160÷2
=80(千米)
320÷80=4(小时)
6时+4时=10时
答:不能,行驶全程要4小时,要10:00到达。
【点睛】本题考查图上距离、实际距离和比例尺的关系,以及行程问题中的基本数量关系“路程÷速度=时间”。
11.路程和时间成正比例;从济南到郑州需要5.5小时
【分析】根据正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。可以判断路程和时间成正比例关系,再解设未知量,根据“速度一定”列出比例,进而利用比例的基本性质求解。
【详解】因为速度(一定),所以路程和时间成正比例。
解:设从济南到郑州需要个小时,
答:从济南到郑州需要5.5小时。
【点睛】此题考查对正比例意义的理解,以及用列比例解决问题的方法和步骤。
12.(1)南偏西;45°;1800;(2)南偏东;50°;1200;(3)见详解
【分析】(1)依据地图上的方向辨别方法,即“上北下南,左西右东”先断定飞霞阁的方位及度数,然后再根据比例尺的计算方法计算出实际距离即可;
(2)依据地图上的方向辨别方法,即“上北下南,左西右东”先断定玉龙潭的方位及度数,然后再根据比例尺的计算方法计算出实际距离即可;
(3)利用比例尺和实际距离计算图上距离,结合题干所给信息完成做题
【详解】(1)600×3=1800(米)
(2)600×2=1200(米)
(3)2400÷600=4(厘米)
【点睛】本题考查依据方向、角度和距离判断物体位置的方法及线段比例尺的意义。
13.6小时
【分析】已知图上距离和比例尺,用图上距离除以比例尺,得实际距离,再用实际距离除以60,本题得以解答。
【详解】7.2÷=7.2×5000000=36000000(cm)=360(km)
360÷60=6(小时)
答:6小时能到达。
【点睛】本题考查了比例尺的运用和路程问题。用图上距离除以比例尺,得实际距离是解答本题的关键。
14.9.6厘米
【分析】按照一定的比例进行图形放缩时,每条边是按照相同的比例放大的,这里长从6厘米变成14.4厘米,用14.4÷6,求出扩大的倍数,宽也扩大相同的倍数,再用4×扩大的倍数,即可解答。
【详解】14.4÷6=2.4
4×2.4=9.6(厘米)
答:放大后照片的宽是9.6厘米。
【点睛】本题考查的是图形的放缩,长扩大几倍或缩小原来的几分之一,宽也扩大原来的几倍或缩小原来的几分之一。
15.(1)(2,6)
(2)东,南,45
(3)(4)见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此解答即可;
(2)根据位置的相对性,方向相反,距离相同,据此解答即可;
(3)把三角形绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕点C按相同方向旋转相同的度数即可;
(4)将三角形的各个边长的长度扩大到原来的2倍即可。
【详解】(1)在方格图中,三角形的顶点A用数对表示(2,6)。
(2)如果点A在点C的西偏北45°的方向上,那么点C在点A的东偏南45°的方向上。
(3)如图所示:
(3)如图所示:
【点睛】本题考查图形的放大,明确放大的是图形的各个边长是解题的关键。
16.(1)图见详解;点C(9,5)
(2)见详解
(3)图见详解;3
【分析】(1)过三角形与斜边相对的顶点,向对边作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;再根据对数表示的方法:第一个数字表示列,带二个数字表示行,写出点C的位置用数对表示;
(2)根据旋转的特征:将三角形绕点C顺时针旋转90°,点C的位置不动,其余各部分均绕此点按相同的方向旋转相同度数,即可画出旋转后的图形;
(3)每个小格是1平方厘米,根据正方形面积公式:面积=边长×边长,1=1×1,每个小格的边长是1厘米;
按1∶2缩小,即三角形的每条边都缩小到原来的,缩小后的三角形的底是6÷2=3厘米;高是4÷2=2厘米;画出缩小后的三角形,再根据三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】(1)三角形的高见下图;点C(9,5)。
(2)见下图;
(3)1×1=1(平方厘米);边长是1厘米;
底:6÷2=3(厘米);高:4÷2=2(厘米)
三角形面积:3×2÷2
=6÷2
=3(平方厘米)
缩小图形见下图。
【点睛】本题考查画三角形的高,作旋转后的图形,做缩小后的图形,用数对表示位置,以及三角形面积公式的应用。
17.(1)(2,1);(5,1);(2)(3)见详解
【分析】(1)数对的表示方法:(列数,行数),分别找出A、B两点在方格中对应的列数和行数,再用数对表示出来。
(2)已知每个小正方形的面积表示1平方厘米,根据正方形的面积公式可知,每个小正方形的边长为1厘米,所以AB的长度为3厘米,根据三角形的面积公式:S=可知,如果以AB长为底边长,用三角形面积乘2再除以3,即可求出三角形的高,据此即可画出这个面积为6平方厘米的三角形ABC。
(3)把三角形ABC按2∶1放大,即三角形的每一条边放大到原来的2倍,原三角形的底和高分别乘2,得出放大后三角形的底和高,据此画出放大后的图形。
【详解】(1)图中点A的位置用数对(2,1)表示,点B的位置用数对(5,1)表示。
(2)根据分析得,AB=3厘米;
6×2÷3=4(厘米)
画三角形如下图。
(3)作图如下。
【点睛】此题先利用数对表示位置的方法,根据三角形的面积公式并画出三角形,再根据图形的放大与缩小的意义完成作图。
18.63吨
【分析】根据题意可知:工作效率=工作总量÷工作时间(一定),即工作总量和工作时间的比值一定,工作总量和工作时间成正比例关系,设这批货物共有x吨,列比例解答。
【详解】解:设这批货物共有x吨。
36∶4=x∶(3+4)
36∶4=x∶7
4x=36×7
x=63
答:这批货物共有63吨。
【点睛】解答此题的关键是:先判断题中的两种相关联的量成什么比例,并找准对应量。
19.10小时
【分析】用路程÷时间=速度这个数量关系,再结合速度不变这个条件,可以列出比例方程。设时间为未知数x。
【详解】解:设全程需要x小时。
45∶3=150∶x
45x=150×3
45x=450
45x÷45=450÷45
x=10
答:全程需要10小时。
【点睛】本题考查用比例方程解决实际问题,找准数量关系就能列出方程。
20.4.8秒
【分析】把他用5G下载这部电影所用的时间设为未知数,用5G下载这部电影所用的时间∶用4G下载这部电影所用的时间=1∶100,据此解答。
【详解】解:设他用5G下载这部电影要用x秒。
8分钟=480秒
x∶480=1∶100
100x=480
x=480÷100
x=4.8
答:他用5G下载这部电影要用4.8秒。
【点睛】本题考查用比例解决问题,根据比例的基本性质求出未知数的值是解答题目的关键。
21.0.64升
【分析】防疫时间消毒液按消毒剂与水的比为1∶10的比例稀释,可得消毒剂∶水=1∶10,据此列比例解答即可。
【详解】解:设需要加入x升消毒剂。
x∶6.4=1∶10
10x=6.4×1
10x÷10=6.4÷10
x=0.64
答:需要加入0.64升消毒剂。
【点睛】根据题意分析得出“消毒剂∶水=1∶10”是解答本题的关键。
22.27天
【分析】根据题意可知,每天修的米数是一定的,也就是修的米数与所用天数成正比例,据此列比例解答。
【详解】解:设修完这条公路共需要x天。
900∶15=(720+900)∶x
900x=24300
x=27
答:这条公路共需要27天。
【点睛】此题考查了比例的应用,明确变化的两个量是比值一定还是乘积一定是解题关键。
23.48千米/时
【分析】已知比例尺和A、B两地间的图上距离,根据“实际距离=图上距离÷比例尺”,求出A、B两地的实际距离,再根据“1千米=100000厘米”换算单位;
已知客车和货车同时从A、B两地相对开出,5小时后相遇,根据“速度和=路程÷相遇时间”,求出两车的速度和;
又已知客车和货车的速度比是3∶2,即货车的速度占两车速度和的,用两车的速度和乘,即可求出货车的速度。
【详解】A、B两地的实际距离:
12÷
=12×5000000
=60000000(厘米)
60000000厘米=600千米
客车与货车的速度和:
600÷5=120(千米/时)
货车的速度:
120×=48(千米/时)
答:货车的速度是48千米/时。
【点睛】本题考查比例尺的应用,相遇问题以及按比分配问题,掌握图上距离、实际距离、比例尺之间的关系,以及速度、时间、路程之间的关系,求出A、B两地的实际距离和两车的速度和,再根据按比分配问题的解题方法解答。
24.8000元;6000元
【分析】可以设兄弟两人月收入分别为4x元,3x元,由于月结余均3600元,由此即可知道兄弟两人分别花的钱数,即4x-3600;3x-3600,由于月支出的比为11∶6,由此即可根据比例的意义列出方程,即(4x-3600)∶(3x-3600)=11∶6,再根据比例的基本性质和等式的性质解方程即可,之后再分别乘兄弟两人月收入的份数即可。
【详解】解:设兄弟两人月收入分别为4x元,3x元
(4x-3600)∶(3x-3600)=11∶6
6×(4x-3600)=11×(3x-3600)
24x-21600=33x-39600
33x-24x=39600-21600
9x=18000
x=18000÷9
x=2000
2000×4=8000(元)
2000×3=6000(元)
答:兄弟两人每个月的收入分别是8000元、6000元。
【点睛】本题主要考查比例的应用,要找准等量关系是解答关键。
25.160米
【分析】火车过桥问题,总路程=桥长+车长,速度一定,路程与时间成正比例。
【详解】解:设这列火车长x米。
(2000+x)∶60=(1460+x)∶45
60x-45x=90000-87600
x=160
答:这列火车长160米。
【点睛】此题考查火车过桥问题路程的特点以及正比例的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版六年级下册第二单元比例解决问题专项突破三
一、解答题
1.按要求完成下面各题。
(1)以学校为观测点,文化宫在学校的( )偏( )( )°方向( )km处;体育馆在学校的( )偏( )( )°方向( )km处。
(2)图书馆在学校南偏西45°方向2km处,公园在学校东偏北20°方向3km处。在图中标出图书馆和公园的位置。
2.在比例尺为1∶1000000的地图上,量得甲,乙两地的距离为8厘米,一辆汽车以每小时80千米的速度从甲地出发开往乙地,经过几小时可以到达乙地?
3.按要求填空。(测量图上距高时取整厘米)
(1)学校到街心花园的实际距为900米,这幅图的比例尺是( )。
(2)足球场在街心花园的( )偏( )°方向( )米处。
(3)游泳馆在街心花园南偏西30°方向600米处,请在图中用“Y”标出它的位置。
4.在比例尺是1∶7500000的地图上,量得甲、乙两地相距12厘米,一辆汽车以每小时60千米的速度从甲地开往乙地,需要多少小时能走完全程?
5.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
6.学校食堂运来30袋大米,每袋,第1周(5天)用了照这样计算,这批大米能用多少天?(列比例解答)
7.小明一家人从甲城出发去丙城旅游,途中要经过乙城,如图所示,他们全程共行驶了多少千米?(测量结果取整厘米数)
8.一块长方形地长和宽的比是7∶4,将其画在比例尺为1∶1000的图纸上,所得图形的周长是44厘米。这块地的实际面积是多少平方米?
9.在一幅比例尺是1∶300000的地图上,量得A、B两地的距离是15厘米,请你计算出A、B两地之间的实际距离是多少千米?
10.在标有的地图上,量得南京到上海的距离为8厘米。暑假期间家住南京的李磊同学全家开车前往上海,早上6:00出发,到达第一个收费站时已经行了160千米,李磊的爸爸看了看手表,此时刚好是8:00,照这样的速度,他们9:50能到达上海吗?
11.科技的发展改善了我们的生活,也改变了人们的出行方式,人们可以选择的交通工具多种多样,如:地铁、汽车、高铁、火车、飞机等。据了解,从济南到郑州的公路长是440km。若一辆车2小时行了160km,照这样计算,从济南到郑州需要多少个小时?先说说路程和时间成什么比例,再用比例解。
12.下图是南山风景区的平面图。
(1)飞霞阁在林峰塔( )( )方向( )米处。
(2)玉龙潭在林峰塔( )( )方向( )米处。
(3)荷花池在林峰塔东偏北40°方向2400米处。请在图中画出荷花池的位置。
13.在比例尺是1∶5000000的地图上,量的甲、乙两地的距离是7.2cm,一辆汽车从甲地开往乙地,每小时行60km,几小时能到达?
14.丽丽去动物园游玩,回家后把一张照片(如图)在电脑上按一定的比例放大,放大后照片的长是14.4厘米,放大后照片的宽是多少厘米?
15.下图中每个小方格表示1cm2,按要求作答。
(1)在方格图中,三角形的顶点A用数对表示( , )。
(2)如果点A在点C的西偏北45°的方向上,那么点C在点A的( )偏( )( )°的方向上。
(3)画出三角形绕点C顺时针旋转90°后的图形。
(4)在方格图中的空白处,画出三角形ABC按2∶1放大后的图形,并标上A′B′C′。
16.图中每个小方格表示1平方厘米。
(1)画出这个直角三角形斜边上的高。点C的位置用数对表示是( )。
(2)画出图中的三角形绕点C顺时针旋转90°的图形。
(3)把原三角形按1∶2缩小,画出缩小后的图形。缩小后三角形的面积是( )平方厘米。
17.(1)图中点A的位置用数对( )表示,点B的位置用数对( )表示。
(2)图中每个小正方形的面积表示1平方厘米,请以AB为一条边,画一个面积是6平方厘米的三角形ABC。
(3)将三角形ABC按2∶1放大后画在方格纸上。
18.货车运一批货物,4天运了36吨。照这样的效率,再运3天就能运完。这批货物共有多少吨?(用比例解)
19.一辆货车前往武汉灾区运送救灾物资,3小时行驶了45千米。从出发地到灾区150千米,按照这样的速度,全程需要多少小时?(列比例解答)
20.2020年我国正式进入5G时代。目前5G正以更快的速度、更稳定的连接与更大的容量融入各行各业。小明原来用4G下载电影《流浪地球》需要8分钟,而他现在用5G下载这部电影所用的时间与用4G下载所用时间的比是1∶100。那么他用5G下载这部电影要用多少秒?(用比例解)
21.防疫时期,教室地面和桌子表面需要消毒。桶里放有6.4升水,根据说明,需加入多少消毒剂?(用比例解答)
22.某工程队修一条路,15天共修900米,还剩下720米没有修。照这样的速度,修完这条公路共需要多少天?(尝试用比例的方法解,可得6分,其它方法解得5分)
23.在一幅比例尺为1∶5000000的地图上,量得A、B两地间公路全长是12厘米。一辆客车和一辆货车同时从A、B两地相对开出,5小时后相遇。已知客车和货车的速度比是3∶2,货车的速度是多少千米/时?
24.兄弟两人月收入的比为4∶3,月支出比为11∶6,月结余均为3600元,问每人每月收入多少元?
25.一列火车通过一座长2000米的大桥要60秒,如果用同样的速度通过一座1460米的隧道则要45秒,这列火车长多少米?(利用比例知识解答)
参考答案
1.(1)西;北;30;3,南;东;40;2
(2)见详解
【分析】(1)地图上的方位是“上北下南,左西右东”,比例尺是图上1厘米表示实际1千米,利用比例尺和图上距离,得出实际距离,据此解答;
(2)根据比例尺和实际距离可计算出图上距离,图书馆距离学校2厘米,公园距离学校3厘米,再结合所给的角度及图上确定方向的方法确定图书馆和公园的位置,并作图即可。
【详解】(1) 以学校为观测点,文化宫在学校的西偏北30°方向3km处;体育馆在学校的南偏东40°方向2km处。
(2)
【点睛】掌握地图的方位及比例尺的意义是解答本题的关键。
2.1小时
【分析】已知比例尺和图上距离求实际距离,依据“实际距离=图上距离÷比例尺”即可求出实际距离,再根据路程÷速度=时间,列式解答。
【详解】8÷
=8×1000000
=8000000(厘米)
=80(千米)
80÷80=1(小时)
答:经过1小时可以到达。
【点睛】此题主要考查比例尺的意义及已知比例尺和图上距离求实际距离,注意单位的换算。
3.(1)1∶30000
(2)东,北60;1200
(3)见详解
【分析】(1)用尺子测量,即可知道学校到街心花园的距离是3厘米,实际距离是900米,根据比例尺的公式:比例尺=图上距离∶实际距离,把数代入公式即可求解,要注意统一单位。
(2)根据地图上的方向(上北下南,左西右东),即可找出足球场在街心花园的方向,之后量出街心花园到足球场的图上距离,再根据公式:实际距离=图上距离÷比例尺,求出实际距离。
(3)图上距离=实际距离×比例尺,求出图上距离,再根据地图上的方向(上北下南,左西右东),即可找出游泳馆的位置。
【详解】(1)900米=90000厘米
3厘米∶90000厘米
=(3÷3)∶(90000÷3)
=1∶30000
所以这幅图的比例尺是:1∶30000
(2)足球场在街心花园图上距离4厘米处
4×30000=120000(厘米)
120000厘米=1200米
即足球场在街心花园的北偏东60°方向1200米。
(3)600米=60000厘米
60000×=2(厘米)
如下图所示:
【点睛】本题主要学会找准方向,并熟练掌握图上距离和实际距离的关系是解题的关键。
4.15小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,即可解答。
【详解】12÷
=12×7500000
=90000000(厘米)
90000000厘米=900千米
900÷60=15(小时)
答:需要15小时能走完全程。
【点睛】本题考查实际距离和图上距离的换算,以及利用速度、时间和距离三者关系进行解答,注意单位名数的换算。
5.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
【点睛】本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
6.15天
【分析】根据题意可知,每天用大米的质量是一定的,每天用大米的质量=总质量÷天数,据此列比例解答。
【详解】解:设这批大米能用x天。
400x=6000
x=15
答:这批大米能用15天。
【点睛】此题考查了比例的实际应用,找出相关的量是比值一定还是乘积一定是解题关键。
7.600千米
【分析】先量出从甲城出发途经乙城去丙城的图上距离,再根据比例尺求出实际距离,解答即可。
【详解】如图:
量出从甲城出发途经乙城去丙城的图上距离是1+2=3(厘米)
3×20000000=60000000(厘米)
60000000厘米=600千米
答:全程共行驶600千米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
8.11200平方米
【分析】依据长方形的周长公式求出长方形的长与宽的和,长与宽的比是7∶4,根据按比分配的方法求出长方形的长和宽的图上长度;再依据“实际距离=图上距离÷比例尺”即可求出这块地的长和宽的实际长度,从而利用长方形的面积公式求出实际面积。
【详解】44÷2=22(厘米)
22×
=22×
=14(厘米)
22×
=22×
=8(厘米)
14÷=14×1000=14000(厘米)=140(米)
8×=8×1000=8000(厘米)=80(米)
140×80=11200(平方米)
答:这块地的实际面积是11200平方米。
【点睛】此题主要考查长方形的周长和面积的计算方法在实际生活中的应用以及图上距离、实际距离和比例尺的关系。
9.45千米
【分析】根据实际距离=图上距离÷比例尺,代入数据计算即可;注意单位的换算:1千米=100000厘米。
【详解】15÷=4500000(厘米)
4500000厘米=45千米
答:A、B两地之间的实际距离是45千米。
【点睛】掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
10.不能,行驶全程要4小时,要10:00到达
【分析】根据比例尺可知图上1厘米表示实际距离40千米,所以用40×8可求出南京到上海的实际距离,又知2小时行了160千米,所以可求出汽车的速度,用南京到上海的实际距离除以汽车的速度就是行完全程所以需要的时间,再与计划时间比较得解。
【详解】40×8=320(千米)
160÷(8-6)
=160÷2
=80(千米)
320÷80=4(小时)
6时+4时=10时
答:不能,行驶全程要4小时,要10:00到达。
【点睛】本题考查图上距离、实际距离和比例尺的关系,以及行程问题中的基本数量关系“路程÷速度=时间”。
11.路程和时间成正比例;从济南到郑州需要5.5小时
【分析】根据正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。可以判断路程和时间成正比例关系,再解设未知量,根据“速度一定”列出比例,进而利用比例的基本性质求解。
【详解】因为速度(一定),所以路程和时间成正比例。
解:设从济南到郑州需要个小时,
答:从济南到郑州需要5.5小时。
【点睛】此题考查对正比例意义的理解,以及用列比例解决问题的方法和步骤。
12.(1)南偏西;45°;1800;(2)南偏东;50°;1200;(3)见详解
【分析】(1)依据地图上的方向辨别方法,即“上北下南,左西右东”先断定飞霞阁的方位及度数,然后再根据比例尺的计算方法计算出实际距离即可;
(2)依据地图上的方向辨别方法,即“上北下南,左西右东”先断定玉龙潭的方位及度数,然后再根据比例尺的计算方法计算出实际距离即可;
(3)利用比例尺和实际距离计算图上距离,结合题干所给信息完成做题
【详解】(1)600×3=1800(米)
(2)600×2=1200(米)
(3)2400÷600=4(厘米)
【点睛】本题考查依据方向、角度和距离判断物体位置的方法及线段比例尺的意义。
13.6小时
【分析】已知图上距离和比例尺,用图上距离除以比例尺,得实际距离,再用实际距离除以60,本题得以解答。
【详解】7.2÷=7.2×5000000=36000000(cm)=360(km)
360÷60=6(小时)
答:6小时能到达。
【点睛】本题考查了比例尺的运用和路程问题。用图上距离除以比例尺,得实际距离是解答本题的关键。
14.9.6厘米
【分析】按照一定的比例进行图形放缩时,每条边是按照相同的比例放大的,这里长从6厘米变成14.4厘米,用14.4÷6,求出扩大的倍数,宽也扩大相同的倍数,再用4×扩大的倍数,即可解答。
【详解】14.4÷6=2.4
4×2.4=9.6(厘米)
答:放大后照片的宽是9.6厘米。
【点睛】本题考查的是图形的放缩,长扩大几倍或缩小原来的几分之一,宽也扩大原来的几倍或缩小原来的几分之一。
15.(1)(2,6)
(2)东,南,45
(3)(4)见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此解答即可;
(2)根据位置的相对性,方向相反,距离相同,据此解答即可;
(3)把三角形绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕点C按相同方向旋转相同的度数即可;
(4)将三角形的各个边长的长度扩大到原来的2倍即可。
【详解】(1)在方格图中,三角形的顶点A用数对表示(2,6)。
(2)如果点A在点C的西偏北45°的方向上,那么点C在点A的东偏南45°的方向上。
(3)如图所示:
(3)如图所示:
【点睛】本题考查图形的放大,明确放大的是图形的各个边长是解题的关键。
16.(1)图见详解;点C(9,5)
(2)见详解
(3)图见详解;3
【分析】(1)过三角形与斜边相对的顶点,向对边作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;再根据对数表示的方法:第一个数字表示列,带二个数字表示行,写出点C的位置用数对表示;
(2)根据旋转的特征:将三角形绕点C顺时针旋转90°,点C的位置不动,其余各部分均绕此点按相同的方向旋转相同度数,即可画出旋转后的图形;
(3)每个小格是1平方厘米,根据正方形面积公式:面积=边长×边长,1=1×1,每个小格的边长是1厘米;
按1∶2缩小,即三角形的每条边都缩小到原来的,缩小后的三角形的底是6÷2=3厘米;高是4÷2=2厘米;画出缩小后的三角形,再根据三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】(1)三角形的高见下图;点C(9,5)。
(2)见下图;
(3)1×1=1(平方厘米);边长是1厘米;
底:6÷2=3(厘米);高:4÷2=2(厘米)
三角形面积:3×2÷2
=6÷2
=3(平方厘米)
缩小图形见下图。
【点睛】本题考查画三角形的高,作旋转后的图形,做缩小后的图形,用数对表示位置,以及三角形面积公式的应用。
17.(1)(2,1);(5,1);(2)(3)见详解
【分析】(1)数对的表示方法:(列数,行数),分别找出A、B两点在方格中对应的列数和行数,再用数对表示出来。
(2)已知每个小正方形的面积表示1平方厘米,根据正方形的面积公式可知,每个小正方形的边长为1厘米,所以AB的长度为3厘米,根据三角形的面积公式:S=可知,如果以AB长为底边长,用三角形面积乘2再除以3,即可求出三角形的高,据此即可画出这个面积为6平方厘米的三角形ABC。
(3)把三角形ABC按2∶1放大,即三角形的每一条边放大到原来的2倍,原三角形的底和高分别乘2,得出放大后三角形的底和高,据此画出放大后的图形。
【详解】(1)图中点A的位置用数对(2,1)表示,点B的位置用数对(5,1)表示。
(2)根据分析得,AB=3厘米;
6×2÷3=4(厘米)
画三角形如下图。
(3)作图如下。
【点睛】此题先利用数对表示位置的方法,根据三角形的面积公式并画出三角形,再根据图形的放大与缩小的意义完成作图。
18.63吨
【分析】根据题意可知:工作效率=工作总量÷工作时间(一定),即工作总量和工作时间的比值一定,工作总量和工作时间成正比例关系,设这批货物共有x吨,列比例解答。
【详解】解:设这批货物共有x吨。
36∶4=x∶(3+4)
36∶4=x∶7
4x=36×7
x=63
答:这批货物共有63吨。
【点睛】解答此题的关键是:先判断题中的两种相关联的量成什么比例,并找准对应量。
19.10小时
【分析】用路程÷时间=速度这个数量关系,再结合速度不变这个条件,可以列出比例方程。设时间为未知数x。
【详解】解:设全程需要x小时。
45∶3=150∶x
45x=150×3
45x=450
45x÷45=450÷45
x=10
答:全程需要10小时。
【点睛】本题考查用比例方程解决实际问题,找准数量关系就能列出方程。
20.4.8秒
【分析】把他用5G下载这部电影所用的时间设为未知数,用5G下载这部电影所用的时间∶用4G下载这部电影所用的时间=1∶100,据此解答。
【详解】解:设他用5G下载这部电影要用x秒。
8分钟=480秒
x∶480=1∶100
100x=480
x=480÷100
x=4.8
答:他用5G下载这部电影要用4.8秒。
【点睛】本题考查用比例解决问题,根据比例的基本性质求出未知数的值是解答题目的关键。
21.0.64升
【分析】防疫时间消毒液按消毒剂与水的比为1∶10的比例稀释,可得消毒剂∶水=1∶10,据此列比例解答即可。
【详解】解:设需要加入x升消毒剂。
x∶6.4=1∶10
10x=6.4×1
10x÷10=6.4÷10
x=0.64
答:需要加入0.64升消毒剂。
【点睛】根据题意分析得出“消毒剂∶水=1∶10”是解答本题的关键。
22.27天
【分析】根据题意可知,每天修的米数是一定的,也就是修的米数与所用天数成正比例,据此列比例解答。
【详解】解:设修完这条公路共需要x天。
900∶15=(720+900)∶x
900x=24300
x=27
答:这条公路共需要27天。
【点睛】此题考查了比例的应用,明确变化的两个量是比值一定还是乘积一定是解题关键。
23.48千米/时
【分析】已知比例尺和A、B两地间的图上距离,根据“实际距离=图上距离÷比例尺”,求出A、B两地的实际距离,再根据“1千米=100000厘米”换算单位;
已知客车和货车同时从A、B两地相对开出,5小时后相遇,根据“速度和=路程÷相遇时间”,求出两车的速度和;
又已知客车和货车的速度比是3∶2,即货车的速度占两车速度和的,用两车的速度和乘,即可求出货车的速度。
【详解】A、B两地的实际距离:
12÷
=12×5000000
=60000000(厘米)
60000000厘米=600千米
客车与货车的速度和:
600÷5=120(千米/时)
货车的速度:
120×=48(千米/时)
答:货车的速度是48千米/时。
【点睛】本题考查比例尺的应用,相遇问题以及按比分配问题,掌握图上距离、实际距离、比例尺之间的关系,以及速度、时间、路程之间的关系,求出A、B两地的实际距离和两车的速度和,再根据按比分配问题的解题方法解答。
24.8000元;6000元
【分析】可以设兄弟两人月收入分别为4x元,3x元,由于月结余均3600元,由此即可知道兄弟两人分别花的钱数,即4x-3600;3x-3600,由于月支出的比为11∶6,由此即可根据比例的意义列出方程,即(4x-3600)∶(3x-3600)=11∶6,再根据比例的基本性质和等式的性质解方程即可,之后再分别乘兄弟两人月收入的份数即可。
【详解】解:设兄弟两人月收入分别为4x元,3x元
(4x-3600)∶(3x-3600)=11∶6
6×(4x-3600)=11×(3x-3600)
24x-21600=33x-39600
33x-24x=39600-21600
9x=18000
x=18000÷9
x=2000
2000×4=8000(元)
2000×3=6000(元)
答:兄弟两人每个月的收入分别是8000元、6000元。
【点睛】本题主要考查比例的应用,要找准等量关系是解答关键。
25.160米
【分析】火车过桥问题,总路程=桥长+车长,速度一定,路程与时间成正比例。
【详解】解:设这列火车长x米。
(2000+x)∶60=(1460+x)∶45
60x-45x=90000-87600
x=160
答:这列火车长160米。
【点睛】此题考查火车过桥问题路程的特点以及正比例的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
