北师大版六年级下册第一单元圆柱与圆锥解决问题专项突破三(含答案)
文档属性
| 名称 | 北师大版六年级下册第一单元圆柱与圆锥解决问题专项突破三(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 565.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 21:25:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版六年级下册第一单元圆柱与圆锥解决问题专项突破三
一、解答题
1.一个圆柱形木料,底面直径20厘米,长5米,它的表面积和体积各是多少?
2.一个圆柱形饼干筒的侧面贴着商标纸,圆柱底面半径是4cm,高是15cm。这张商标纸的面积是多少?
3.世博园中哈萨克毡房给明明留下了深刻的印象,它独具异域风情,由一个近似的圆柱和一个近似的圆锥组成。这个毡房里面的空间大约是多少立方米?
4.一个圆锥形的麦堆,底面周长是15.7米,高1.2米。如果每立方米小麦约重700千克,那么这堆小麦约重多少千克?
5.做一个无盖的圆柱形铁皮水桶,高是6分米,底面半径是4分米,做这个桶至少需要铁皮多少平方分米?
6.一个圆柱形蓄水池,底面直径是8米,如果向这个池注入1.5米深的水,需要多少升水?
7.一个注满水的圆柱形储水池,池口周长是62.8米。灌溉花园用去一些水后,水面下降了20厘米,用去的水跟剩下的水的比正好是1∶5,这个水池的容积是多少?
8.把一块棱长10厘米的正方体铁块铸成一个底面直径20厘米的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
9.制作一个无盖圆柱形水桶,有四种型号的铁皮可供选择(不考虑损耗)。
(1)要恰好做成水桶,有几种选择方案?
(2)算一算哪种方案做成的水桶容积最大?最大是多少?
10.2014年一个叫滕飞的中国小伙成功在内蒙古奈曼沙漠中种植出“沙漠水稻”,被称为第二个“袁隆平”。
(1)滕飞和他的团队的沙漠中打了几口直径2米,70米深的机井为水稻灌溉。每个机井要挖出多少立方米的沙子?
(2)2014年,500亩试验田成功收获了120吨稻谷,为每户当地老百姓带来3万元的纯收入。到2017年发展到32000亩,每户老百姓收入提高了45%,2017年每户老百姓收入多少万元?
11.在一个长12.56厘米、宽8厘米、高10厘米的长方体水箱中,放入一个底面半径3厘米的圆锥形铁块后(铁块完全浸没),水面上升了0.3厘米(水未溢出),圆锥形铁块的高是多少厘米?
12.一台压路机的滚筒长50分米,半径0.4米,如果每分钟滚动10周,半小时压路面积是多少?
13.下图是一个长5厘米、宽3厘米的长方形。
(1)画一条线段将这个长方形分成一个等腰三角形和一个梯形;
(2)梯形的面积是( )平方厘米;
(3)如果以上图中得到的三角形的任意一条直角边为轴,将这个三角形旋转一周,所得到的立体图形的体积是多少?
14.阳光社区为了加强绿地建设,准备建一个底面直径是20米,高是0.3米的圆柱形花坛。(以下问题中花坛壁的厚度都忽略不计)
(1)这个圆柱形花坛的占地面积是多少平方米?
(2)如果在花坛外侧贴瓷砖,那么贴瓷砖的面积一共是多少平方米?
(3)现有一个圆锥形的土堆,经测量,土堆的底面周长是31.4米,高是3米。这堆土能否填满这个花坛?写出你的判断理由。
15.一个圆锥形沙堆,底面直径是4米,高是0.6米。把这堆沙平铺在长方体沙坑里,能铺多少厘米厚?
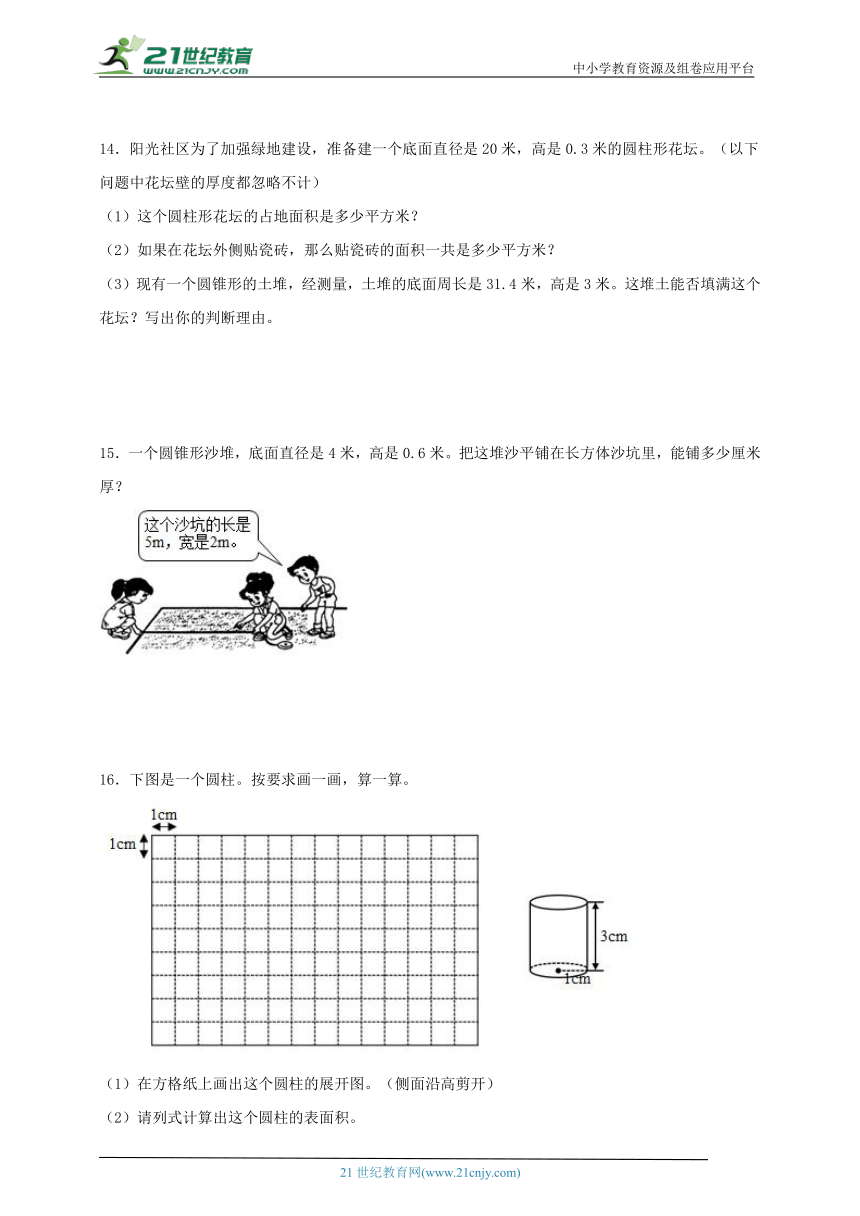
16.下图是一个圆柱。按要求画一画,算一算。
(1)在方格纸上画出这个圆柱的展开图。(侧面沿高剪开)
(2)请列式计算出这个圆柱的表面积。
17.母亲节时,小明送给妈妈一只茶杯(如图)。茶杯中部的一圈装饰带很漂亮,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,做装饰带至少用料多少平方厘米?(接头处忽略不计)
18.2018年12月8日,我国发射的“嫦娥四号”月球探测器上携带的“月面微型生态圈”开启了人类进行月面生物实验的篇章,科学家在这个小空间里创造动植物生长环境,实现生态循环。它高18厘米,直径16厘米,是一个由特殊铝合金材料制成的圆柱体(如图所示)。尽管这个圆柱体净容积只有约0.8升,总重量仅3千克但内含乾坤:里面放置着马铃薯种子、拟南芥种子、蚕卵、土壤、水、空气以及照相机和信息传输系统等科研设备。你知道这个“月面微型生态圈”的表面积大约是多少吗?(圆柱体容器上的功能键忽略不计)
19.下图是一瓶已经喝了一些的果汁和一个圆锥形玻璃环,如果把瓶中的果汁倒入这个圆锥形玻璃杯中,那么可以倒满多少杯?(单位:厘米)
20.张医生定做了一个药箱,从侧面看是由一个半圆和一个正方形组成。(如图)
(1)如果忽略厚度不计,这个药箱的容积是多少?
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是多少?
21.一个圆锥形沙堆,底面积是31.4平方米,高是2.4米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
22.一张长方形铁皮,长18.84分米,宽6分米,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少平方分米?水桶的容积是多少?
23.张叔叔有两张铝板,规格如下图:
现在张叔叔要用以上两张铝板做一个圆柱形有盖的桶,如何设计,才能使做出来的桶能装容纳更多的物体?
(1)请把你的方案画出来,并标出相关数据。
(2)你所设计的桶最多能装多长升水?(结果保留整数)
24.一个内直径是10厘米的瓶子里,水的高度有12厘米,把瓶盖拧紧后倒置放平,无水部分是圆柱形,高10厘米。这个瓶子的容积是多少升?
25.有一张长方形铁皮,如图剪下阴影部分制成铁桶,求这个铁桶的容积。(单位:分米)
参考答案
1.32028平方厘米;157000立方厘米
【分析】先根据进率1米=100厘米,把5米换算成500厘米;再根据圆柱的表面积公式S表=S侧+2S底,其中S侧=πdh,S底=πr2;圆柱的体积公式V=πr2h,分别代入数据计算即可。
【详解】5米=500厘米
3.14×20×500+3.14×(20÷2)2×2
=3.14×10000+3.14×100×2
=31400+628
=32028(平方厘米)
3.14×(20÷2)2×500
=3.14×100×500
=314×500
=157000(立方厘米)
答:它的表面积是32028平方厘米,它的体积是157000立方厘米。
【点睛】掌握圆柱的表面积、体积计算公式是解题的关键。
2.376.8cm2
【分析】根据题意,求商标纸的面积,商标纸贴在圆柱形饼干筒的侧面,所以是求圆柱的侧面积,根据公式S侧=2πrh,代入数据计算即可。
【详解】2×3.14×4×15
=6.28×4×15
=25.12×15
=376.8(cm2)
答:这张商标纸的面积是376.8cm2。
【点睛】本题考查圆柱侧面积的实际应用,掌握圆柱的侧面积公式是解题的关键。
3.65.94立方米
【分析】求这个毡房的空间,就是求这个毡房的体积,毡房的体积有底面直径是6米,高是2米的圆柱形的体积与底面直径为6米,高为1米的圆锥形的体积的和;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,即可解答。
【详解】3.14×(6÷2)2×2+3.14×(6÷2)2×1×
=3.14×9×2+3.14×9×1×
=28.26×2+28.26×1×
=56.52+28.26×
=56.52+9.42
=65.94(立方米)
答:这个毡房里面的空间大约是65.94平方米。
【点睛】熟练掌握和运用圆柱体积公式和圆锥体积公式,是解答本题的关键。
4.5495千克
【分析】根据圆的周长公式:周长=π÷3.14÷2,代入数据,求出圆锥的底面半径;再根据圆锥的体积公式:体积=底面积×高×;代入数据,求出圆锥形的麦堆的体积,再乘700千克,即可求出这堆小麦约重多少千克。
【详解】15.7÷3.14÷2
=5÷2
=2.5(米)
3.14×2.52×1.2××700
=3.14×6.25×1.2××700
=19.625×1.2××700
=23.55××700
=7.85×700
=5495(千克)
答:这堆小麦约重5495千克。
【点睛】熟练掌握和灵活运用圆锥体积公式和圆的周长公式,是解答本题的关键。
5.200.96平方分米
【分析】求做这个桶至少需要铁皮多少平方分米,就是求这个圆柱形铁皮桶的表面积,根据圆柱的表面积公式:底面积×2+侧面积;又因为是无盖,表面积=圆柱的底面积+侧面积,代入数据,即可解答。
【详解】3.14×42+3.14×4×2×6
=3.14×16+12.56×2×6
=50.24+25.12×6
=50.24+150.72
=200.96(平方分米)
答:做这个桶至少需要铁皮200.96平方分米。
【点睛】熟练掌握圆柱表面积公式是解答本题的关键,注意是无盖桶。
6.75360升
【分析】此题实际是求圆柱体的体积的问题,根据圆柱的体积公式:,把数据代入公式解答。
【详解】3.14×(8÷2)2×1.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方米)
75.36立方米=75360升
答:需要75360升水。
【点睛】此题主要考查圆柱的体积公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算。
7.376.8立方米
【分析】根据水池池口周长计算出圆柱的底面积,根据下降的水面高度利用圆柱的体积公式求出用去水的体积,用去的水跟剩下的水的比正好是1∶5,则用去水的体积占整个水池容积的,根据“量÷对应的分率”求出水池的容积,据此解答。
【详解】20厘米=0.2米
底面积:3.14×(62.8÷3.14÷2)2
=3.14×(20÷2)2
=3.14×102
=314(平方米)
水池容积:314×0.2÷
=62.8÷
=376.8(立方米)
答:这个水池的容积是376.8立方米。
【点睛】掌握圆柱的体积(容积)公式和按比例分配问题的解题方法是解答题目的关键。
8.10厘米
【分析】由题意可知,正方体铁块的体积等于圆锥形铁块的体积,先求出正方体的体积,然后根据圆锥的体积公式变形:h=3V÷S,据此解答即可。
【详解】10×10×10
=100×10
=1000(立方厘米)
3×1000÷[3.14×(20÷2)2]
=3000÷[3.14×100]
=3000÷314
≈10(厘米)
答:这个圆锥形铁块的高约是10厘米。
【点睛】本题考查正方体和圆锥的体积,熟记公式是解题的关键。
9.(1)2种选择方案
(2)②和③水桶容积最多;最大:50.24cm3
【分析】(1)圆和长方形恰好做成水桶,就是圆的周长等于长方形的一条边,根据圆的周长公式:π×直径,代入数据,求出圆的周长,在图中找到相同长度的边长的长方形即可;
(2)根据圆柱的容积公式:容积=底面积×高;代入数据,计算出制作水桶的容积,再进行比较,即可解答。
【详解】(1)②的周长:3.14×4=12.56(cm)
④的周长:3.14×3=9.42(cm)
①和④恰好做成水桶;②和③恰好做成水桶;一共有2种方案。
答:有2种选择方案。
(2)①和④恰好做成水桶的容积:
3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=7.065×2
=14.13(cm3)
②和③恰好做成水桶的容积:
3.14×(4÷2)2×4
=3.14×22×4
=3.14×4×4
=12.56×4
=50.24(cm3)
50.24>14.13
②和③恰好做成水桶的容积最多。
答:②和③恰好做成水桶的容积最多,最大是50.24cm3。
【点睛】利用圆的周长公式、圆柱的展开图以及圆柱的容积公式进行解答,解题的关键是熟记公式。
10.(1)219.8立方米
(2)4.35万元
【分析】(1)求每个机井要挖出多少立方米沙子,就是求直径为2米,高为70米的圆柱的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答;
(2)把2014年的纯收入看作单位“1”,2017年老百姓收入提高了45%,2017年的收入是2014年收入的(1+45%),用2014年的纯收入×(1+45%),即可求出2017年的老百姓的收入。
【详解】(1)3.14×(2÷2)2×70
=3.14×1×70
=219.8(立方米)
答:每个机井要挖出219.8立方米的沙子。
(2)3×(1+45%)
=3×1.45
=4.35(万元)
答:2017年每户老百姓的收入是4.35万元。
【点睛】熟练掌握和运用圆柱的体积公式和比一个数多或少百分之几的数是多少的知识进行解答。
11.3.2厘米
【分析】根据题意知:把圆锥形铁块放长方体水箱中,上升部分水的体积就是这个圆锥形铁块的体积,根据长方体体积公式:V=abh,圆锥的体积公式:V=,可得,把数据代入公式解答即可。
【详解】12.56×8×0.3×3÷(3.14×3×3)
=30.144×3÷(3.14×9)
=90.432÷28.26
=3.2(厘米)
答:圆锥形铁块的高是3.2厘米。
【点睛】本题主要考查长方体的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
12.3768平方米
【分析】滚筒是圆柱形的,先求出滚筒的侧面积,再将其乘10,求出滚筒每分钟压路的面积,最后将每分钟压路面积乘30分钟,即可求出半小时的压路面积。
【详解】50分米=5米,半小时=30分钟
(2×0.4×3.14×5)×10×30
=12.56×10×30
=3768(平方米)
答:半小时的压路面积是3768平方米。
【点睛】本题考查了圆柱侧面积的应用,圆柱侧面积=底面周长×高。
13.(1)见详解;
(2)10.5;
(3)28.26立方厘米
【分析】(1)在长方形的长上取宽的长度,连接它的端点和长方形对角的端点,从而将这个长方形分成一个等腰三角形和一个梯形;
(2)看图,这个梯形的上底是2厘米,下底是5厘米,高是3厘米,将数据代入梯形的面积公式,求出这个梯形的面积;
(3)将这个直角三角形旋转一周,得到了一个圆锥,这个圆锥的底面半径是3厘米,高是3厘米,由此将数据代入圆锥的体积公式中,求出它的体积。
【详解】(1)如图:
(2)(5-3+5)×3÷2
=7×3÷2
=10.5(平方厘米)
所以,这个梯形的面积是10.5平方厘米。
(3)3.14×32×3×=28.26(立方厘米)
答:所得的立体图形的体积是28.26立方厘米。
【点睛】本题考查了梯形的面积和圆锥的体积,梯形的面积=(上底+下底)×高÷2,圆锥的体积=×底面积×高。
14.(1)314平方米
(2)18.84平方米
(3)不能填满,理由见详解
【分析】(1)求花坛的占地面积就是求圆柱的底面积。圆柱的底面积=πr2,据此解答。
(2)贴瓷砖的面积就是圆柱的侧面积。圆柱的侧面积=底面周长×高,据此解答。
(3)圆的周长=2πr,据此用圆锥的底面周长除以2π即可求出圆锥的底面半径。圆柱的体积=底面积×高,圆锥的体积=底面积×高×,据此分别求出圆柱形花坛的容积和圆锥形土堆的体积,再进行比较即可解答。
【详解】(1)3.14×(20÷2)2
=3.14×100
=314(平方米)
答:这个圆柱形花坛的占地面积是314平方米。
(2)3.14×20×0.3
=62.8×0.3
=18.84(平方米)
答:贴瓷砖的面积一共是18.84平方米。
(3)314×0.3=94.2(立方米)
31.4÷3.14÷2=5米
×3.14×52×3
=3.14×25
=78.5(立方米)
78.5<94.2
答:这堆土不能填满这个花坛。
【点睛】本题考查了圆柱的底面积和侧面积、圆柱和圆锥体积的实际应用。要熟练掌握相关计算公式并灵活运用。
15.25.12厘米
【分析】先利用“”求出这堆沙的体积,再根据“铺沙的厚度=这堆沙的体积÷(长方体沙坑的长×长方体沙坑的宽)”求出所铺沙子的厚度,最后把单位转化为厘米,据此解答。
【详解】
(立方米)
2.512÷(5×2)×100
=2.512÷10×100
=0.2512×100
=25.12(厘米)
答:能铺25.12厘米厚。
【点睛】熟练运用圆柱体和长方体的体积计算公式是解答题目的关键。
16.(1)见详解;
(2)25.12cm2
【分析】(1)圆柱侧面沿高剪开成一个长方形,长是圆柱的底面周长,宽是圆柱的高,底面展开是两个圆;据此解答;
(2)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,代入数据计算即可。
【详解】(1)底面周长:3.14×1×2
=3.14×2
=6.28(cm)
画图如下:
(2)3.14×1×1×2+6.28×3
=6.28+18.84
=25.12(cm2)
答:这个圆柱的表面积是25.12cm2。
【点睛】本题主要考查圆柱展开图及圆柱的表面积公式。
17.94.2平方厘米
【分析】圆柱的侧面展开图是一个长方形,宽是5厘米,长是圆柱底面周长。
【详解】3.14×6×5
=3.14×30
=94.2(平方厘米)
答:做装饰带至少用料94.2平方厘米。
【点睛】本题主要考查了学生对圆柱表面积的展开图的理解,及他们想象能力。
18.1306.24平方厘米
【分析】根据圆柱的面积公式=2×底面积+侧面积,圆柱的底面积:,侧面积=底面周长()×高,将数据代入,据此即可得出答案。
【详解】2×3.14×(16÷2)2+3.14×16×18
=6.28×82+50.24×18
=6.28×64+904.32
=401.92+904.32
=1306.24(平方厘米)
答:这个“月面微型生态圈”的表面积大约是1306.24平方厘米。
【点睛】本题考查学生对圆柱表面积公式的掌握和运用,要求学生熟练掌握。
19.6杯
【分析】根据圆柱的体积公式:圆柱体积=底面积×高,圆锥的体积=底面积×高×,带入数据,求出圆柱瓶里果汁的体积和圆锥形玻璃杯的体积,再用果汁的体积除以圆锥形玻璃杯的体积,即可解答。
【详解】3.14×(10÷2)2×(8+8)÷[3.14×(10÷2)2×8×]
=3.14×25×16÷[3.14×25×8×]
=78.5×16÷[78.5×8×]
=1256÷[628×]
=1256÷
=1256×
=6(杯)
答:可以倒满6杯。
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
20.(1)27.85立方分米
(2)46.84平方分米
【分析】(1)这个药箱的容积包括一个长方体的容积和半个圆柱的体积,利用长方体的体积公式:体积=长×宽×高;圆柱的体积公式:体积=底面积×高;代入数据求出长方体的体积和半个圆柱的体积,再相加,即可解答。
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是指4个长方体的面和圆柱的一个底面积和圆柱侧面积的一半,根据长方形面积公式:长×宽;圆柱的表面积公式:底面面积+侧面积÷2,代入数据,求出面积,再相加,即可解答。
【详解】(1)5×2×2+3.14×(2÷2)2×5÷2
=10×2+3.14×1×5÷2
=20+3.14×5÷2
=20+15.7÷2
=20+7.85
=27.85(立方分米)
答:这个药箱的容积是27.85立方分米。
(2)2×2×2+2×5×2+3.14×2×5÷2+3.14×(2÷2)2
=4×2+10×2+6.28×5÷2+3.14×1
=8+20+31.4÷2+3.14
=8+20+15.7+3.14
=28+15.7+3.14
=43.7+3.14
=46.84(平方分米)
答:刷漆的面积是46.84平方分米。
【点睛】本题考查了长方体和圆柱体积公式及表面积公式的应用;关键是熟记公式。
21.125.6米
【分析】先根据圆锥的体积公式求得圆锥形沙堆的体积;再将路面看作一个长方体,它的体积等于圆锥形沙堆的体积,根据长方体的体积公式可求能铺路面的长度。
【详解】2厘米=0.02米
×31.4×2.4÷(10×0.02)
=×75.36÷0.2
=25.12÷0.2
=125.6(米)
答:能铺125.6米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
22.表面积是141.3平方分米,容积是169.56升
【分析】由题意可知,这个水桶的表面积等于水桶的侧面积加上一个底面的面积,根据根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,圆柱的体积(容积)公式:V=Sh,把数据代入公式解答。
【详解】18.84×6+3.14×(18.84÷3.14÷2)2
=113.04+3.14×9
=113.04+28.26
=141.3(平方分米)
3.14×(18.84÷3.14÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
169.56立方分米=169.56升
答:这个铁皮水桶的表面积是141.3平方分米,桶的容积是169.56升。
【点睛】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
23.(1)见详解
(2)635升
【分析】(1)用边长为20分米的正方形铝板做桶的侧面,这样的桶容积才能最大、这时桶的底面直径是20÷3.14≈6.37(分米),在长13分米 ,宽7分米的铝板上可以剪出两个直径6.4分米的桶盖。
(2)用半径2×3.14×20得桶的容积。
【详解】(1)
(2)(20÷3.14÷2)2×3.14×20
≈3.182×3.14×20
≈635.05(立方分米)
≈635(立方分米)
≈635升
答: 桶最多能装635升水。
【点睛】通过桶的侧面积求得桶的底面积,再利用底面积乘高求得容积是解答本题的关键。
24.1.727升
【分析】瓶子不管怎么放置,瓶子空余部分的容积不变,先把瓶子倒置把空余部分转化为规则图形,不管是有水的圆柱还是空余部分的圆柱,它们的内直径都是10厘米,有水的圆柱的高是12厘米,空余部分的圆柱的高是10厘米,根据圆柱的体积公式V=πr2h作答此题。
【详解】r=10÷2=5(厘米)
3.14×52×12+3.14×52×10
=3.14×25×(12+10)
=3.14×25×22
=1727(立方厘米)
1727立方厘米=1727毫升=1.727升
答:这个瓶子的容积是1.727升。
【点睛】这是一道关于圆柱的体积计算的题目,理解前后两次瓶子的放置,后面空余部分就是前面的空余部分的解题的关键。
25.113.04立方分米
【分析】由图可知:铁桶的底面周长是18.84,带入圆的周长公式求出底面直径。再用长方形的宽减去底面直径求出铁桶的高,最后带入圆柱的容积公式即可解答。
【详解】18.84÷3.14=6(分米)
10-6=4(分米)
3.14×(6÷2)2×4
=3.14×9×4
=3.14×36
=113.04(立方分米)
答:这个铁桶的容积是113.04立方分米。
【点睛】本题主要考查圆柱的容积公式,求出铁桶的底面直径及高是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版六年级下册第一单元圆柱与圆锥解决问题专项突破三
一、解答题
1.一个圆柱形木料,底面直径20厘米,长5米,它的表面积和体积各是多少?
2.一个圆柱形饼干筒的侧面贴着商标纸,圆柱底面半径是4cm,高是15cm。这张商标纸的面积是多少?
3.世博园中哈萨克毡房给明明留下了深刻的印象,它独具异域风情,由一个近似的圆柱和一个近似的圆锥组成。这个毡房里面的空间大约是多少立方米?
4.一个圆锥形的麦堆,底面周长是15.7米,高1.2米。如果每立方米小麦约重700千克,那么这堆小麦约重多少千克?
5.做一个无盖的圆柱形铁皮水桶,高是6分米,底面半径是4分米,做这个桶至少需要铁皮多少平方分米?
6.一个圆柱形蓄水池,底面直径是8米,如果向这个池注入1.5米深的水,需要多少升水?
7.一个注满水的圆柱形储水池,池口周长是62.8米。灌溉花园用去一些水后,水面下降了20厘米,用去的水跟剩下的水的比正好是1∶5,这个水池的容积是多少?
8.把一块棱长10厘米的正方体铁块铸成一个底面直径20厘米的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
9.制作一个无盖圆柱形水桶,有四种型号的铁皮可供选择(不考虑损耗)。
(1)要恰好做成水桶,有几种选择方案?
(2)算一算哪种方案做成的水桶容积最大?最大是多少?
10.2014年一个叫滕飞的中国小伙成功在内蒙古奈曼沙漠中种植出“沙漠水稻”,被称为第二个“袁隆平”。
(1)滕飞和他的团队的沙漠中打了几口直径2米,70米深的机井为水稻灌溉。每个机井要挖出多少立方米的沙子?
(2)2014年,500亩试验田成功收获了120吨稻谷,为每户当地老百姓带来3万元的纯收入。到2017年发展到32000亩,每户老百姓收入提高了45%,2017年每户老百姓收入多少万元?
11.在一个长12.56厘米、宽8厘米、高10厘米的长方体水箱中,放入一个底面半径3厘米的圆锥形铁块后(铁块完全浸没),水面上升了0.3厘米(水未溢出),圆锥形铁块的高是多少厘米?
12.一台压路机的滚筒长50分米,半径0.4米,如果每分钟滚动10周,半小时压路面积是多少?
13.下图是一个长5厘米、宽3厘米的长方形。
(1)画一条线段将这个长方形分成一个等腰三角形和一个梯形;
(2)梯形的面积是( )平方厘米;
(3)如果以上图中得到的三角形的任意一条直角边为轴,将这个三角形旋转一周,所得到的立体图形的体积是多少?
14.阳光社区为了加强绿地建设,准备建一个底面直径是20米,高是0.3米的圆柱形花坛。(以下问题中花坛壁的厚度都忽略不计)
(1)这个圆柱形花坛的占地面积是多少平方米?
(2)如果在花坛外侧贴瓷砖,那么贴瓷砖的面积一共是多少平方米?
(3)现有一个圆锥形的土堆,经测量,土堆的底面周长是31.4米,高是3米。这堆土能否填满这个花坛?写出你的判断理由。
15.一个圆锥形沙堆,底面直径是4米,高是0.6米。把这堆沙平铺在长方体沙坑里,能铺多少厘米厚?
16.下图是一个圆柱。按要求画一画,算一算。
(1)在方格纸上画出这个圆柱的展开图。(侧面沿高剪开)
(2)请列式计算出这个圆柱的表面积。
17.母亲节时,小明送给妈妈一只茶杯(如图)。茶杯中部的一圈装饰带很漂亮,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,做装饰带至少用料多少平方厘米?(接头处忽略不计)
18.2018年12月8日,我国发射的“嫦娥四号”月球探测器上携带的“月面微型生态圈”开启了人类进行月面生物实验的篇章,科学家在这个小空间里创造动植物生长环境,实现生态循环。它高18厘米,直径16厘米,是一个由特殊铝合金材料制成的圆柱体(如图所示)。尽管这个圆柱体净容积只有约0.8升,总重量仅3千克但内含乾坤:里面放置着马铃薯种子、拟南芥种子、蚕卵、土壤、水、空气以及照相机和信息传输系统等科研设备。你知道这个“月面微型生态圈”的表面积大约是多少吗?(圆柱体容器上的功能键忽略不计)
19.下图是一瓶已经喝了一些的果汁和一个圆锥形玻璃环,如果把瓶中的果汁倒入这个圆锥形玻璃杯中,那么可以倒满多少杯?(单位:厘米)
20.张医生定做了一个药箱,从侧面看是由一个半圆和一个正方形组成。(如图)
(1)如果忽略厚度不计,这个药箱的容积是多少?
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是多少?
21.一个圆锥形沙堆,底面积是31.4平方米,高是2.4米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
22.一张长方形铁皮,长18.84分米,宽6分米,用这张铁皮卷成一个圆柱形铁皮水桶的侧面,另配一个底面制成一个最大的水桶。这个铁皮水桶的表面积是多少平方分米?水桶的容积是多少?
23.张叔叔有两张铝板,规格如下图:
现在张叔叔要用以上两张铝板做一个圆柱形有盖的桶,如何设计,才能使做出来的桶能装容纳更多的物体?
(1)请把你的方案画出来,并标出相关数据。
(2)你所设计的桶最多能装多长升水?(结果保留整数)
24.一个内直径是10厘米的瓶子里,水的高度有12厘米,把瓶盖拧紧后倒置放平,无水部分是圆柱形,高10厘米。这个瓶子的容积是多少升?
25.有一张长方形铁皮,如图剪下阴影部分制成铁桶,求这个铁桶的容积。(单位:分米)
参考答案
1.32028平方厘米;157000立方厘米
【分析】先根据进率1米=100厘米,把5米换算成500厘米;再根据圆柱的表面积公式S表=S侧+2S底,其中S侧=πdh,S底=πr2;圆柱的体积公式V=πr2h,分别代入数据计算即可。
【详解】5米=500厘米
3.14×20×500+3.14×(20÷2)2×2
=3.14×10000+3.14×100×2
=31400+628
=32028(平方厘米)
3.14×(20÷2)2×500
=3.14×100×500
=314×500
=157000(立方厘米)
答:它的表面积是32028平方厘米,它的体积是157000立方厘米。
【点睛】掌握圆柱的表面积、体积计算公式是解题的关键。
2.376.8cm2
【分析】根据题意,求商标纸的面积,商标纸贴在圆柱形饼干筒的侧面,所以是求圆柱的侧面积,根据公式S侧=2πrh,代入数据计算即可。
【详解】2×3.14×4×15
=6.28×4×15
=25.12×15
=376.8(cm2)
答:这张商标纸的面积是376.8cm2。
【点睛】本题考查圆柱侧面积的实际应用,掌握圆柱的侧面积公式是解题的关键。
3.65.94立方米
【分析】求这个毡房的空间,就是求这个毡房的体积,毡房的体积有底面直径是6米,高是2米的圆柱形的体积与底面直径为6米,高为1米的圆锥形的体积的和;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,即可解答。
【详解】3.14×(6÷2)2×2+3.14×(6÷2)2×1×
=3.14×9×2+3.14×9×1×
=28.26×2+28.26×1×
=56.52+28.26×
=56.52+9.42
=65.94(立方米)
答:这个毡房里面的空间大约是65.94平方米。
【点睛】熟练掌握和运用圆柱体积公式和圆锥体积公式,是解答本题的关键。
4.5495千克
【分析】根据圆的周长公式:周长=π÷3.14÷2,代入数据,求出圆锥的底面半径;再根据圆锥的体积公式:体积=底面积×高×;代入数据,求出圆锥形的麦堆的体积,再乘700千克,即可求出这堆小麦约重多少千克。
【详解】15.7÷3.14÷2
=5÷2
=2.5(米)
3.14×2.52×1.2××700
=3.14×6.25×1.2××700
=19.625×1.2××700
=23.55××700
=7.85×700
=5495(千克)
答:这堆小麦约重5495千克。
【点睛】熟练掌握和灵活运用圆锥体积公式和圆的周长公式,是解答本题的关键。
5.200.96平方分米
【分析】求做这个桶至少需要铁皮多少平方分米,就是求这个圆柱形铁皮桶的表面积,根据圆柱的表面积公式:底面积×2+侧面积;又因为是无盖,表面积=圆柱的底面积+侧面积,代入数据,即可解答。
【详解】3.14×42+3.14×4×2×6
=3.14×16+12.56×2×6
=50.24+25.12×6
=50.24+150.72
=200.96(平方分米)
答:做这个桶至少需要铁皮200.96平方分米。
【点睛】熟练掌握圆柱表面积公式是解答本题的关键,注意是无盖桶。
6.75360升
【分析】此题实际是求圆柱体的体积的问题,根据圆柱的体积公式:,把数据代入公式解答。
【详解】3.14×(8÷2)2×1.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方米)
75.36立方米=75360升
答:需要75360升水。
【点睛】此题主要考查圆柱的体积公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算。
7.376.8立方米
【分析】根据水池池口周长计算出圆柱的底面积,根据下降的水面高度利用圆柱的体积公式求出用去水的体积,用去的水跟剩下的水的比正好是1∶5,则用去水的体积占整个水池容积的,根据“量÷对应的分率”求出水池的容积,据此解答。
【详解】20厘米=0.2米
底面积:3.14×(62.8÷3.14÷2)2
=3.14×(20÷2)2
=3.14×102
=314(平方米)
水池容积:314×0.2÷
=62.8÷
=376.8(立方米)
答:这个水池的容积是376.8立方米。
【点睛】掌握圆柱的体积(容积)公式和按比例分配问题的解题方法是解答题目的关键。
8.10厘米
【分析】由题意可知,正方体铁块的体积等于圆锥形铁块的体积,先求出正方体的体积,然后根据圆锥的体积公式变形:h=3V÷S,据此解答即可。
【详解】10×10×10
=100×10
=1000(立方厘米)
3×1000÷[3.14×(20÷2)2]
=3000÷[3.14×100]
=3000÷314
≈10(厘米)
答:这个圆锥形铁块的高约是10厘米。
【点睛】本题考查正方体和圆锥的体积,熟记公式是解题的关键。
9.(1)2种选择方案
(2)②和③水桶容积最多;最大:50.24cm3
【分析】(1)圆和长方形恰好做成水桶,就是圆的周长等于长方形的一条边,根据圆的周长公式:π×直径,代入数据,求出圆的周长,在图中找到相同长度的边长的长方形即可;
(2)根据圆柱的容积公式:容积=底面积×高;代入数据,计算出制作水桶的容积,再进行比较,即可解答。
【详解】(1)②的周长:3.14×4=12.56(cm)
④的周长:3.14×3=9.42(cm)
①和④恰好做成水桶;②和③恰好做成水桶;一共有2种方案。
答:有2种选择方案。
(2)①和④恰好做成水桶的容积:
3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=7.065×2
=14.13(cm3)
②和③恰好做成水桶的容积:
3.14×(4÷2)2×4
=3.14×22×4
=3.14×4×4
=12.56×4
=50.24(cm3)
50.24>14.13
②和③恰好做成水桶的容积最多。
答:②和③恰好做成水桶的容积最多,最大是50.24cm3。
【点睛】利用圆的周长公式、圆柱的展开图以及圆柱的容积公式进行解答,解题的关键是熟记公式。
10.(1)219.8立方米
(2)4.35万元
【分析】(1)求每个机井要挖出多少立方米沙子,就是求直径为2米,高为70米的圆柱的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答;
(2)把2014年的纯收入看作单位“1”,2017年老百姓收入提高了45%,2017年的收入是2014年收入的(1+45%),用2014年的纯收入×(1+45%),即可求出2017年的老百姓的收入。
【详解】(1)3.14×(2÷2)2×70
=3.14×1×70
=219.8(立方米)
答:每个机井要挖出219.8立方米的沙子。
(2)3×(1+45%)
=3×1.45
=4.35(万元)
答:2017年每户老百姓的收入是4.35万元。
【点睛】熟练掌握和运用圆柱的体积公式和比一个数多或少百分之几的数是多少的知识进行解答。
11.3.2厘米
【分析】根据题意知:把圆锥形铁块放长方体水箱中,上升部分水的体积就是这个圆锥形铁块的体积,根据长方体体积公式:V=abh,圆锥的体积公式:V=,可得,把数据代入公式解答即可。
【详解】12.56×8×0.3×3÷(3.14×3×3)
=30.144×3÷(3.14×9)
=90.432÷28.26
=3.2(厘米)
答:圆锥形铁块的高是3.2厘米。
【点睛】本题主要考查长方体的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
12.3768平方米
【分析】滚筒是圆柱形的,先求出滚筒的侧面积,再将其乘10,求出滚筒每分钟压路的面积,最后将每分钟压路面积乘30分钟,即可求出半小时的压路面积。
【详解】50分米=5米,半小时=30分钟
(2×0.4×3.14×5)×10×30
=12.56×10×30
=3768(平方米)
答:半小时的压路面积是3768平方米。
【点睛】本题考查了圆柱侧面积的应用,圆柱侧面积=底面周长×高。
13.(1)见详解;
(2)10.5;
(3)28.26立方厘米
【分析】(1)在长方形的长上取宽的长度,连接它的端点和长方形对角的端点,从而将这个长方形分成一个等腰三角形和一个梯形;
(2)看图,这个梯形的上底是2厘米,下底是5厘米,高是3厘米,将数据代入梯形的面积公式,求出这个梯形的面积;
(3)将这个直角三角形旋转一周,得到了一个圆锥,这个圆锥的底面半径是3厘米,高是3厘米,由此将数据代入圆锥的体积公式中,求出它的体积。
【详解】(1)如图:
(2)(5-3+5)×3÷2
=7×3÷2
=10.5(平方厘米)
所以,这个梯形的面积是10.5平方厘米。
(3)3.14×32×3×=28.26(立方厘米)
答:所得的立体图形的体积是28.26立方厘米。
【点睛】本题考查了梯形的面积和圆锥的体积,梯形的面积=(上底+下底)×高÷2,圆锥的体积=×底面积×高。
14.(1)314平方米
(2)18.84平方米
(3)不能填满,理由见详解
【分析】(1)求花坛的占地面积就是求圆柱的底面积。圆柱的底面积=πr2,据此解答。
(2)贴瓷砖的面积就是圆柱的侧面积。圆柱的侧面积=底面周长×高,据此解答。
(3)圆的周长=2πr,据此用圆锥的底面周长除以2π即可求出圆锥的底面半径。圆柱的体积=底面积×高,圆锥的体积=底面积×高×,据此分别求出圆柱形花坛的容积和圆锥形土堆的体积,再进行比较即可解答。
【详解】(1)3.14×(20÷2)2
=3.14×100
=314(平方米)
答:这个圆柱形花坛的占地面积是314平方米。
(2)3.14×20×0.3
=62.8×0.3
=18.84(平方米)
答:贴瓷砖的面积一共是18.84平方米。
(3)314×0.3=94.2(立方米)
31.4÷3.14÷2=5米
×3.14×52×3
=3.14×25
=78.5(立方米)
78.5<94.2
答:这堆土不能填满这个花坛。
【点睛】本题考查了圆柱的底面积和侧面积、圆柱和圆锥体积的实际应用。要熟练掌握相关计算公式并灵活运用。
15.25.12厘米
【分析】先利用“”求出这堆沙的体积,再根据“铺沙的厚度=这堆沙的体积÷(长方体沙坑的长×长方体沙坑的宽)”求出所铺沙子的厚度,最后把单位转化为厘米,据此解答。
【详解】
(立方米)
2.512÷(5×2)×100
=2.512÷10×100
=0.2512×100
=25.12(厘米)
答:能铺25.12厘米厚。
【点睛】熟练运用圆柱体和长方体的体积计算公式是解答题目的关键。
16.(1)见详解;
(2)25.12cm2
【分析】(1)圆柱侧面沿高剪开成一个长方形,长是圆柱的底面周长,宽是圆柱的高,底面展开是两个圆;据此解答;
(2)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,代入数据计算即可。
【详解】(1)底面周长:3.14×1×2
=3.14×2
=6.28(cm)
画图如下:
(2)3.14×1×1×2+6.28×3
=6.28+18.84
=25.12(cm2)
答:这个圆柱的表面积是25.12cm2。
【点睛】本题主要考查圆柱展开图及圆柱的表面积公式。
17.94.2平方厘米
【分析】圆柱的侧面展开图是一个长方形,宽是5厘米,长是圆柱底面周长。
【详解】3.14×6×5
=3.14×30
=94.2(平方厘米)
答:做装饰带至少用料94.2平方厘米。
【点睛】本题主要考查了学生对圆柱表面积的展开图的理解,及他们想象能力。
18.1306.24平方厘米
【分析】根据圆柱的面积公式=2×底面积+侧面积,圆柱的底面积:,侧面积=底面周长()×高,将数据代入,据此即可得出答案。
【详解】2×3.14×(16÷2)2+3.14×16×18
=6.28×82+50.24×18
=6.28×64+904.32
=401.92+904.32
=1306.24(平方厘米)
答:这个“月面微型生态圈”的表面积大约是1306.24平方厘米。
【点睛】本题考查学生对圆柱表面积公式的掌握和运用,要求学生熟练掌握。
19.6杯
【分析】根据圆柱的体积公式:圆柱体积=底面积×高,圆锥的体积=底面积×高×,带入数据,求出圆柱瓶里果汁的体积和圆锥形玻璃杯的体积,再用果汁的体积除以圆锥形玻璃杯的体积,即可解答。
【详解】3.14×(10÷2)2×(8+8)÷[3.14×(10÷2)2×8×]
=3.14×25×16÷[3.14×25×8×]
=78.5×16÷[78.5×8×]
=1256÷[628×]
=1256÷
=1256×
=6(杯)
答:可以倒满6杯。
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
20.(1)27.85立方分米
(2)46.84平方分米
【分析】(1)这个药箱的容积包括一个长方体的容积和半个圆柱的体积,利用长方体的体积公式:体积=长×宽×高;圆柱的体积公式:体积=底面积×高;代入数据求出长方体的体积和半个圆柱的体积,再相加,即可解答。
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是指4个长方体的面和圆柱的一个底面积和圆柱侧面积的一半,根据长方形面积公式:长×宽;圆柱的表面积公式:底面面积+侧面积÷2,代入数据,求出面积,再相加,即可解答。
【详解】(1)5×2×2+3.14×(2÷2)2×5÷2
=10×2+3.14×1×5÷2
=20+3.14×5÷2
=20+15.7÷2
=20+7.85
=27.85(立方分米)
答:这个药箱的容积是27.85立方分米。
(2)2×2×2+2×5×2+3.14×2×5÷2+3.14×(2÷2)2
=4×2+10×2+6.28×5÷2+3.14×1
=8+20+31.4÷2+3.14
=8+20+15.7+3.14
=28+15.7+3.14
=43.7+3.14
=46.84(平方分米)
答:刷漆的面积是46.84平方分米。
【点睛】本题考查了长方体和圆柱体积公式及表面积公式的应用;关键是熟记公式。
21.125.6米
【分析】先根据圆锥的体积公式求得圆锥形沙堆的体积;再将路面看作一个长方体,它的体积等于圆锥形沙堆的体积,根据长方体的体积公式可求能铺路面的长度。
【详解】2厘米=0.02米
×31.4×2.4÷(10×0.02)
=×75.36÷0.2
=25.12÷0.2
=125.6(米)
答:能铺125.6米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
22.表面积是141.3平方分米,容积是169.56升
【分析】由题意可知,这个水桶的表面积等于水桶的侧面积加上一个底面的面积,根据根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,圆柱的体积(容积)公式:V=Sh,把数据代入公式解答。
【详解】18.84×6+3.14×(18.84÷3.14÷2)2
=113.04+3.14×9
=113.04+28.26
=141.3(平方分米)
3.14×(18.84÷3.14÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
169.56立方分米=169.56升
答:这个铁皮水桶的表面积是141.3平方分米,桶的容积是169.56升。
【点睛】此题主要考查圆柱的体积公式、圆柱的侧面积公式、圆的面积公式的灵活运用,关键是熟记公式。
23.(1)见详解
(2)635升
【分析】(1)用边长为20分米的正方形铝板做桶的侧面,这样的桶容积才能最大、这时桶的底面直径是20÷3.14≈6.37(分米),在长13分米 ,宽7分米的铝板上可以剪出两个直径6.4分米的桶盖。
(2)用半径2×3.14×20得桶的容积。
【详解】(1)
(2)(20÷3.14÷2)2×3.14×20
≈3.182×3.14×20
≈635.05(立方分米)
≈635(立方分米)
≈635升
答: 桶最多能装635升水。
【点睛】通过桶的侧面积求得桶的底面积,再利用底面积乘高求得容积是解答本题的关键。
24.1.727升
【分析】瓶子不管怎么放置,瓶子空余部分的容积不变,先把瓶子倒置把空余部分转化为规则图形,不管是有水的圆柱还是空余部分的圆柱,它们的内直径都是10厘米,有水的圆柱的高是12厘米,空余部分的圆柱的高是10厘米,根据圆柱的体积公式V=πr2h作答此题。
【详解】r=10÷2=5(厘米)
3.14×52×12+3.14×52×10
=3.14×25×(12+10)
=3.14×25×22
=1727(立方厘米)
1727立方厘米=1727毫升=1.727升
答:这个瓶子的容积是1.727升。
【点睛】这是一道关于圆柱的体积计算的题目,理解前后两次瓶子的放置,后面空余部分就是前面的空余部分的解题的关键。
25.113.04立方分米
【分析】由图可知:铁桶的底面周长是18.84,带入圆的周长公式求出底面直径。再用长方形的宽减去底面直径求出铁桶的高,最后带入圆柱的容积公式即可解答。
【详解】18.84÷3.14=6(分米)
10-6=4(分米)
3.14×(6÷2)2×4
=3.14×9×4
=3.14×36
=113.04(立方分米)
答:这个铁桶的容积是113.04立方分米。
【点睛】本题主要考查圆柱的容积公式,求出铁桶的底面直径及高是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
