广东省惠州重点中学2023-2024学年八年级下学期开学考试数学试题(无答案)
文档属性
| 名称 | 广东省惠州重点中学2023-2024学年八年级下学期开学考试数学试题(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 309.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
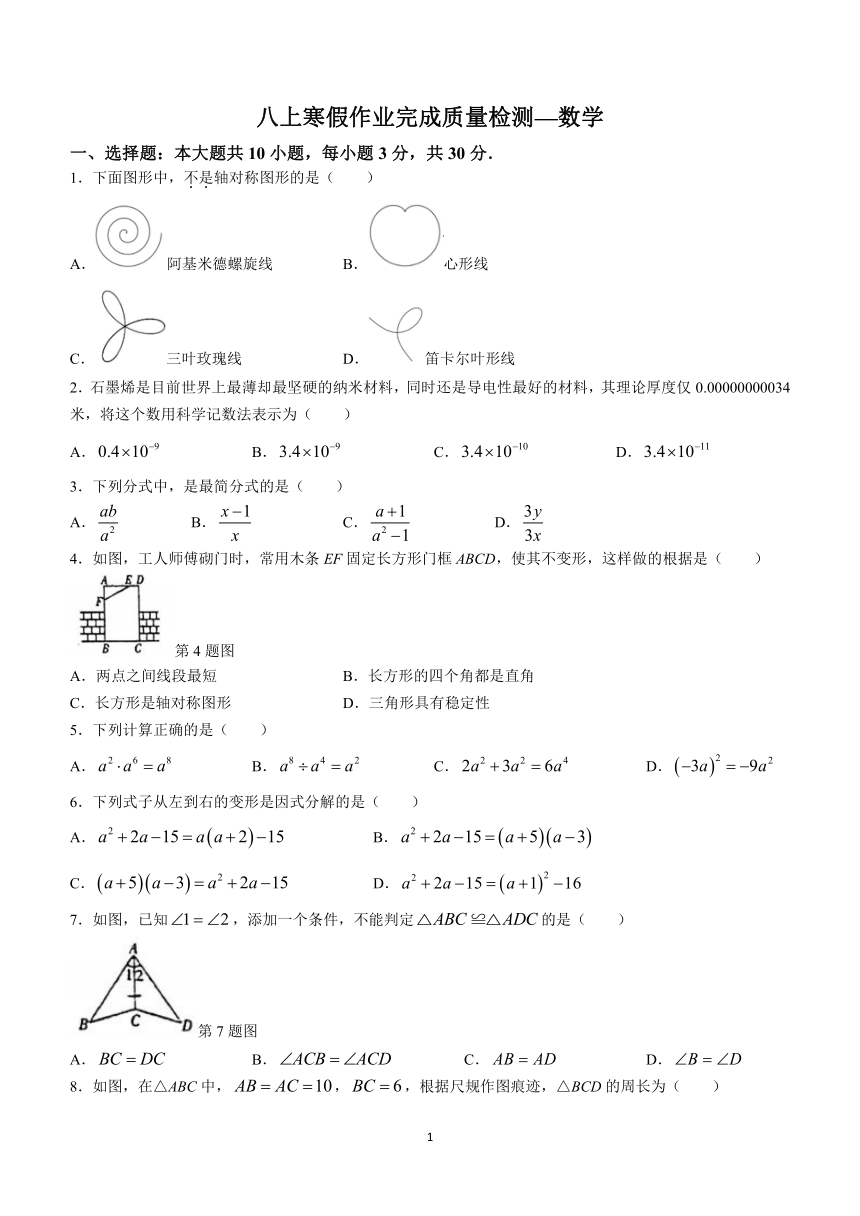
八上寒假作业完成质量检测—数学
一、选择题:本大题共10小题,每小题3分,共30分.
1.下面图形中,不是轴对称图形的是( )
A.阿基米德螺旋线 B.心形线
C.三叶玫瑰线 D.笛卡尔叶形线
2.石墨烯是目前世界上最薄却最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000000034米,将这个数用科学记数法表示为( )
A. B. C. D.
3.下列分式中,是最简分式的是( )
A. B. C. D.
4.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
第4题图
A.两点之间线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形具有稳定性
5.下列计算正确的是( )
A. B. C. D.
6.下列式子从左到右的变形是因式分解的是( )
A. B.
C. D.
7.如图,已知,添加一个条件,不能判定的是( )
第7题图
A. B. C. D.
8.如图,在△ABC中,,,根据尺规作图痕迹,△BCD的周长为( )
第8题图
A.26 B.20 C.16 D.14
9.下列条件中,不能判定△ABC为直角三角形的是( )
A. B.
C. D.
10.如图,平行河岸两侧各有一城镇P、Q,根据发展规划,要修建一条桥梁连接P、Q两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.在平面直角坐标系中,点关于y轴对称的点的坐标为______.
12.若.则______.
13.已知一个多边形的内角和比它的外角和大540°,则该多边形的边数为______.
14.若△ABC的三边长a、b、c均是整数,且满足,则△ABC周长的最大值是______.
15.定义:形如的数称为复数(其中a、b为实数,i为虚数单位,规定),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,如,则的实部是,虚部是6.已知复数的虚部是12,则实部是______.
三、解答题(一):本大题共3小题,共24分.
16.(8分)计算:
(1);(2).
17.(9分)
(1)因式分解:;(2)解分式方程:.
18.(7分)先化简,再求值:,在,0,1,2四个数中选一个合适的代入求值.
四、解答题(二):本大题共3小题,共28分.
19.(10分)习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知1件甲种农机具比1件乙种农机具多1.5万元,用18万元购买甲种农机具的数量和用12万元购买乙种农机具的数量相同.
(1)求购买1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲、乙两种农机具共20件,且购买的总费用不超过72万元,则甲种农机具最多能购买多少件?
20.(9分)如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次轴对称变换后得到(图中已标出点C的对应点).
(1)在给定方格纸中画出;
(2)画出AC边上的中线BD和BC边上的高线AE;
(3)求的面积.
21.(9分)如图,在△ABC中,,,,AB的垂直平分线DE交AC于点D,交AB于点E、连接BD.
(1)求证:;
(2)求BD的长.
五、解答题(三):本大题共2小题,共23分.
22.(11分)如图①,把一个长为2m、宽为2n的长方形,沿虚线剪开,均分成四块小长方形,然后拼成一个正方形(如图②).
(1)请用两种不同的方法表示图②中阴影部分的面积.(用含m、n的式子表示)
方法1:______;
方法2:______;
(2)根据(1)中结论,请你写出式子、、之间的等量关系:______;
(3)根据(2)中的等量关系,解决如下问题:已知实数x,y满足,,则______;
(4)许多代数恒等式可以用图形的面积来表示.如图③,它表示了.试画出一个几何图形,使它的面积能表示:.
图① 图② 图③
23.(12分)如图1,点C在线段AB上(点C不与点A、B重合),分别以AC、BC为一腰在AB同侧作两个等腰三角形ACD和等腰三角形BCE,其中,,,连接AE、交DB于点P.
(1)【观察猜想】
①AE与DB的数量关系是______;
②的度数为______.
(2)【数学思考】
将△BCE绕点C旋转到如图2所示的位置,其他条件不变,上述猜想①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给子证明.
(3)【拓展应用】
在(2)的条件下,求证:.
图1 图2
一、选择题:本大题共10小题,每小题3分,共30分.
1.下面图形中,不是轴对称图形的是( )
A.阿基米德螺旋线 B.心形线
C.三叶玫瑰线 D.笛卡尔叶形线
2.石墨烯是目前世界上最薄却最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000000034米,将这个数用科学记数法表示为( )
A. B. C. D.
3.下列分式中,是最简分式的是( )
A. B. C. D.
4.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
第4题图
A.两点之间线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形具有稳定性
5.下列计算正确的是( )
A. B. C. D.
6.下列式子从左到右的变形是因式分解的是( )
A. B.
C. D.
7.如图,已知,添加一个条件,不能判定的是( )
第7题图
A. B. C. D.
8.如图,在△ABC中,,,根据尺规作图痕迹,△BCD的周长为( )
第8题图
A.26 B.20 C.16 D.14
9.下列条件中,不能判定△ABC为直角三角形的是( )
A. B.
C. D.
10.如图,平行河岸两侧各有一城镇P、Q,根据发展规划,要修建一条桥梁连接P、Q两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.在平面直角坐标系中,点关于y轴对称的点的坐标为______.
12.若.则______.
13.已知一个多边形的内角和比它的外角和大540°,则该多边形的边数为______.
14.若△ABC的三边长a、b、c均是整数,且满足,则△ABC周长的最大值是______.
15.定义:形如的数称为复数(其中a、b为实数,i为虚数单位,规定),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,如,则的实部是,虚部是6.已知复数的虚部是12,则实部是______.
三、解答题(一):本大题共3小题,共24分.
16.(8分)计算:
(1);(2).
17.(9分)
(1)因式分解:;(2)解分式方程:.
18.(7分)先化简,再求值:,在,0,1,2四个数中选一个合适的代入求值.
四、解答题(二):本大题共3小题,共28分.
19.(10分)习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知1件甲种农机具比1件乙种农机具多1.5万元,用18万元购买甲种农机具的数量和用12万元购买乙种农机具的数量相同.
(1)求购买1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲、乙两种农机具共20件,且购买的总费用不超过72万元,则甲种农机具最多能购买多少件?
20.(9分)如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次轴对称变换后得到(图中已标出点C的对应点).
(1)在给定方格纸中画出;
(2)画出AC边上的中线BD和BC边上的高线AE;
(3)求的面积.
21.(9分)如图,在△ABC中,,,,AB的垂直平分线DE交AC于点D,交AB于点E、连接BD.
(1)求证:;
(2)求BD的长.
五、解答题(三):本大题共2小题,共23分.
22.(11分)如图①,把一个长为2m、宽为2n的长方形,沿虚线剪开,均分成四块小长方形,然后拼成一个正方形(如图②).
(1)请用两种不同的方法表示图②中阴影部分的面积.(用含m、n的式子表示)
方法1:______;
方法2:______;
(2)根据(1)中结论,请你写出式子、、之间的等量关系:______;
(3)根据(2)中的等量关系,解决如下问题:已知实数x,y满足,,则______;
(4)许多代数恒等式可以用图形的面积来表示.如图③,它表示了.试画出一个几何图形,使它的面积能表示:.
图① 图② 图③
23.(12分)如图1,点C在线段AB上(点C不与点A、B重合),分别以AC、BC为一腰在AB同侧作两个等腰三角形ACD和等腰三角形BCE,其中,,,连接AE、交DB于点P.
(1)【观察猜想】
①AE与DB的数量关系是______;
②的度数为______.
(2)【数学思考】
将△BCE绕点C旋转到如图2所示的位置,其他条件不变,上述猜想①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给子证明.
(3)【拓展应用】
在(2)的条件下,求证:.
图1 图2
同课章节目录
