青岛版九年级数学上册第2章2.5解直角三角形的应用同步训练题(含答案)
文档属性
| 名称 | 青岛版九年级数学上册第2章2.5解直角三角形的应用同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 07:33:49 | ||
图片预览



文档简介
青岛版九年级数学上册第2章2.5解直角三角形的应用同步训练题(含答案)
一.选择题(共10小题)
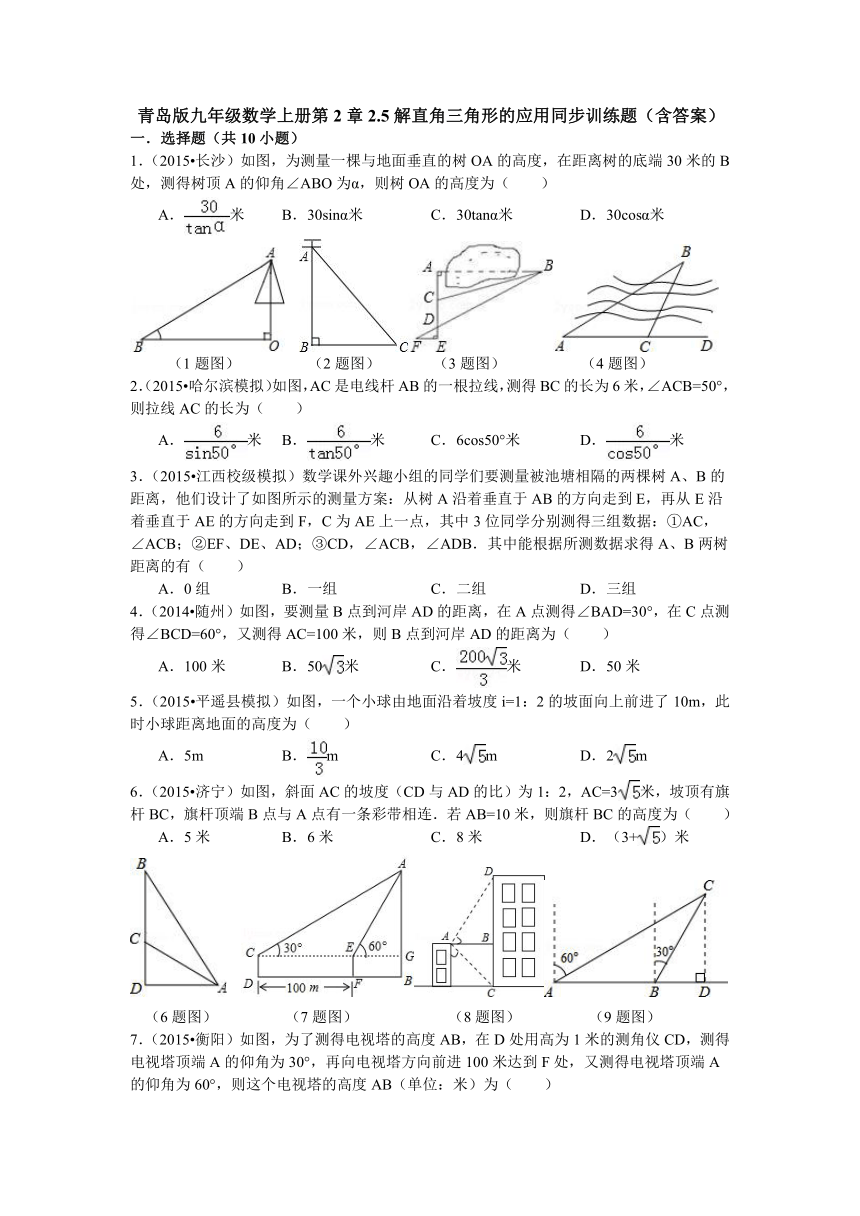
1.(2015 长沙)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B. 30sinα米 C. 30tanα米 D. 30cosα米
(1题图) (2题图) (3题图) (4题图)
2.(2015 哈尔滨模拟)如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.米 B. 米 C. 6cos50°米 D. 米
3.(2015 江西校级模拟)数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B. 一组 C. 二组 D. 三组
4.(2014 随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B. 50米 C. 米 D. 50米
5.(2015 平遥县模拟)如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B. m C. 4m D. 2m
6.(2015 济宁)如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米 B. 6米 C. 8米 D. (3+)米
(6题图) (7题图) (8题图) (9题图)
7.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
8.(2014 百色)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是( )
A.(6+6)米 B. (6+3)米 C. (6+2)米 D. 12米
9.(2015 巴彦淖尔)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B. 40海里 C. 20海里 D. 40海里
10.(2015 泰安)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里 B. 40海里 C. 海里 D. 海里
(10题图) (12题图) (13题图)
二.填空题(共10小题)
11.(2015 大庆模拟)如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为 .
12.(2015 邵阳)如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
13.(2015 泰安模拟)如图,斜坡AC的坡度(坡高比水平距离)为1:,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.旗杆BC的高度是 .
14.(2015 潍坊)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
(14题图) (15题图) (16题图)
15.(2015 荆州)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)
16.(2015 高密市三模)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为 米.
17.(2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
(17题图) (18题图) (19题图) (20题图)
18.(2015 深圳模拟)一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西65°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为 .
19.(2015 东营区校级模拟)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于 海里.
20. (2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
三.解答题(共5小题)
21.(2015 茂名)如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.
(1)求新铺设的输电线路AB的长度;(结果保留根号)
(2)问整改后从A地到B地的输电线路比原来缩短了多少千米?(结果保留根号)
22.(2015 黔南州)如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
23.(2015 安徽)如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(=1.7).
24.(2015 潜江)热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
25.(2015 锦州)如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:≈1.414,结果精确到0.1)
青岛版九年级数学上册第2章2.5解直角三角形的应用同步训练题
参考答案
一.选择题(共10小题)
1.C 2.D 3.D 4.B 5.D 6.A 7.C 8.A 9.C 10.D
二.填空题(共10小题)
11.25米 12.1000 13.6米 14.135 15.137 16.160
17.2km 18.20海里/分 19.10 20. 2km .
三.解答题(共5小题)
21.解:(1)过C作CD⊥AB,交AB于点D,
在Rt△ACD中,CD=AC sin∠CAD=20×=10(千米),AD=AC cos∠CAD=20×=10(千米),
在Rt△BCD中,BD===10(千米),
∴AB=AD+DB=10+10=10(+1)(千米),
则新铺设的输电线路AB的长度10(+1)(千米);
(2)在Rt△BCD中,根据勾股定理得:BC==10(千米),
∴AC+CB﹣AB=20+10﹣(10+10)=10(1+﹣)(千米),
则整改后从A地到B地的输电线路比原来缩短了10(1+﹣)千米.
22.解:需要拆除,理由为:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=:3,即∠CDB=30°,
∴DC=2BC=20米,BD==10米,
∴AD=BD﹣AB=(10﹣10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除.
23.解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=,
∴BE=CE cot30°=12×=12.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12.
∴CD=CE+DE=12(+1)≈32.4.
答:楼房CD的高度约为32.4m.
24.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
25.解:过B作BD⊥AP于D,
由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,
在Rt△ABD中,∵AB=40,∠A=30,
∴BD=AB=20,
在Rt△BDP中,∵∠P=45°,
∴PB=BD=20.
一.选择题(共10小题)
1.(2015 长沙)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B. 30sinα米 C. 30tanα米 D. 30cosα米
(1题图) (2题图) (3题图) (4题图)
2.(2015 哈尔滨模拟)如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.米 B. 米 C. 6cos50°米 D. 米
3.(2015 江西校级模拟)数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B. 一组 C. 二组 D. 三组
4.(2014 随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B. 50米 C. 米 D. 50米
5.(2015 平遥县模拟)如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B. m C. 4m D. 2m
6.(2015 济宁)如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米 B. 6米 C. 8米 D. (3+)米
(6题图) (7题图) (8题图) (9题图)
7.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
8.(2014 百色)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是( )
A.(6+6)米 B. (6+3)米 C. (6+2)米 D. 12米
9.(2015 巴彦淖尔)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B. 40海里 C. 20海里 D. 40海里
10.(2015 泰安)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里 B. 40海里 C. 海里 D. 海里
(10题图) (12题图) (13题图)
二.填空题(共10小题)
11.(2015 大庆模拟)如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为 .
12.(2015 邵阳)如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
13.(2015 泰安模拟)如图,斜坡AC的坡度(坡高比水平距离)为1:,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.旗杆BC的高度是 .
14.(2015 潍坊)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
(14题图) (15题图) (16题图)
15.(2015 荆州)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)
16.(2015 高密市三模)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为 米.
17.(2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
(17题图) (18题图) (19题图) (20题图)
18.(2015 深圳模拟)一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西65°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为 .
19.(2015 东营区校级模拟)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于 海里.
20. (2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
三.解答题(共5小题)
21.(2015 茂名)如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.
(1)求新铺设的输电线路AB的长度;(结果保留根号)
(2)问整改后从A地到B地的输电线路比原来缩短了多少千米?(结果保留根号)
22.(2015 黔南州)如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
23.(2015 安徽)如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(=1.7).
24.(2015 潜江)热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
25.(2015 锦州)如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:≈1.414,结果精确到0.1)
青岛版九年级数学上册第2章2.5解直角三角形的应用同步训练题
参考答案
一.选择题(共10小题)
1.C 2.D 3.D 4.B 5.D 6.A 7.C 8.A 9.C 10.D
二.填空题(共10小题)
11.25米 12.1000 13.6米 14.135 15.137 16.160
17.2km 18.20海里/分 19.10 20. 2km .
三.解答题(共5小题)
21.解:(1)过C作CD⊥AB,交AB于点D,
在Rt△ACD中,CD=AC sin∠CAD=20×=10(千米),AD=AC cos∠CAD=20×=10(千米),
在Rt△BCD中,BD===10(千米),
∴AB=AD+DB=10+10=10(+1)(千米),
则新铺设的输电线路AB的长度10(+1)(千米);
(2)在Rt△BCD中,根据勾股定理得:BC==10(千米),
∴AC+CB﹣AB=20+10﹣(10+10)=10(1+﹣)(千米),
则整改后从A地到B地的输电线路比原来缩短了10(1+﹣)千米.
22.解:需要拆除,理由为:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=:3,即∠CDB=30°,
∴DC=2BC=20米,BD==10米,
∴AD=BD﹣AB=(10﹣10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除.
23.解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=,
∴BE=CE cot30°=12×=12.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12.
∴CD=CE+DE=12(+1)≈32.4.
答:楼房CD的高度约为32.4m.
24.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
25.解:过B作BD⊥AP于D,
由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,
在Rt△ABD中,∵AB=40,∠A=30,
∴BD=AB=20,
在Rt△BDP中,∵∠P=45°,
∴PB=BD=20.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
