数学人教A版(2019)必修二6.2.1 向量的加法运算 课件(共65张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修二6.2.1 向量的加法运算 课件(共65张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 09:20:49 | ||
图片预览











文档简介
(共65张PPT)
部编版高一数学必修下第一章6.2.1
6.2 平面向量的运算
6.2.1 向量的加法运算
1.数学抽象:阅读和理解向量及向量符号的由来,理解平面向量加法运算的几何意义.
2.直观想象:借助实例和平面向量的几何意义,
3.逻辑推理: 掌握平面向量加法运算及运算规则.
4.数学运算:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
核心素养目标
教学目标
教学重点:1.借助实例和平面向量的几何意义,掌握平面向量加法运算及运算规则.
2.理解平面向量加法运算的几何意义.
3.会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
教学难点:对平面向量加法运算的几何意义的理解.
唉, 哪儿去了
嘻嘻!大笨猫!
B
A
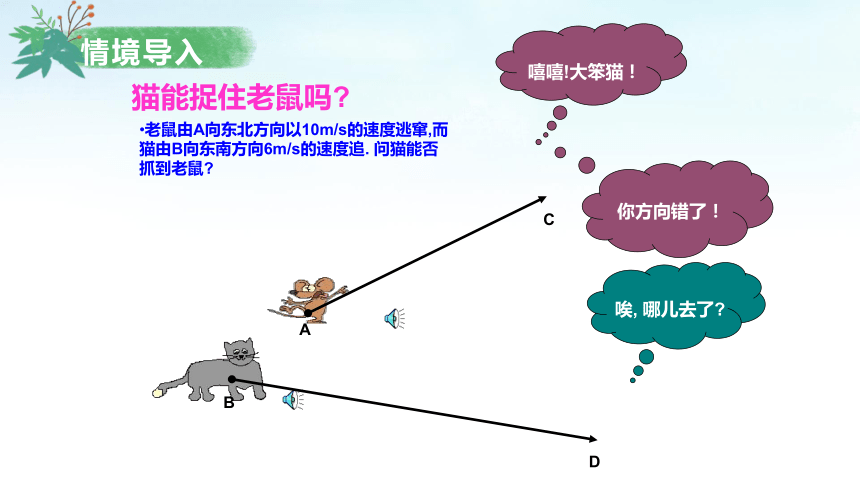
猫能捉住老鼠吗
老鼠由A向东北方向以10m/s的速度逃窜,而猫由B向东南方向6m/s的速度追. 问猫能否抓到老鼠
C
D
你方向错了!
情境导入
情境导入
向量最初被应用于物理学,被称为矢量。
亚里士多德是古希腊著名的科学家,他是柏拉图的学生,亚历山大的老师。大约公元前350年,亚里士多德就知道了力可以表示为向量。
任务探究一
(一)向量的物理背景与概念
1.问:力、速度、加速度、位移有什么共同特点?
向量:既有大小,又有方向的量.
向量的两要素:方向、大小
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
知识拓展
带有方向的线段叫做有向线段.
英国大科学家牛顿(Newton,1642-1727),最先使用有向线段表示向量。
1806年,瑞士人阿尔冈以
表示一个有向线段或向量。
1827年莫比乌斯(1827年)则以 表示起点为A,终点为B的向量,这用法为相当广泛的数学家所接受。
知识拓展
1912年,兰格文用 表示向量,以后,字母上加箭头表示向量的方法逐渐流行, 尤其在手写稿中。一些作者为了方便印刷,以粗黑体小写字母a,b等表示向量。这两种符号一直沿用至今。
知识拓展
(二)向量的表示
1、向量的几何表示:用有向线段表示。
有向线段的三个要素: 起点、方向、长度
向量AB的大小,也就是向量AB的长度(或称模),记作|AB|。
2、向量的字母表示:(1)a , b , c , . . .
(2)用表示向量的有向线段的起点和终点字母
表示,例如,AB,CD
知识拓展
两个特殊的向量
零向量:
长度为0的向量叫做零向量,记作 0.
注:零向量也有方向,并且规定零向量的方向是任意的
单位向量:
长度等于1个单位的向量叫做单位向量.
1.温度含零上和零下温度,所以温度是向量.( )
判断题
×
2.向量的模是一个正实数.( )
×
注:向量不能比较大小
4.若|a|>|b| ,则a 与b就能比较大小 ( )
3.若|a|=0,则a = 0 . ( )
×
×
任务探究二
任务探究三
(三)相等向量与共线向量
1.平行向量、共线向量和相等向量的概念及表示;
2.任意一组平行向量都可以平移到同一直线上吗?
3. 平行向量一定是相等向量吗?
4.相等向量一定是平行向量吗?
5.若非零向量AB//CD ,那么AB//CD吗?
平行向量又叫做共线向量
如:
a
b
c
(1)平行向量:方向相同或相反的非零向量叫做平行向量。
记作 a ∥b ∥c
规定:0与任一向量平行。
问:把一组平行于直线l的向量的起点平移到直线l上的 一点O ,这时它们是不是平行向量?
o
l
.
C
OC = c
A
OA = a
OB = b
B
(三)相等向量与共线向量
任务探究四
向量相等 向量平行
平行向量一定是相等向量吗
相等向量一定是平行向量吗
(2)相等向量:长度相等且方向相同的向量叫做相等向量。
记作:a = b
a
b
1.若非零向量AB//CD ,那么AB//CD吗?
2.若a//b ,则a与b的方向一定相同或相反吗?
o
.
b
a
注:向量可任意平行移动.
(三)相等向量与共线向量
任务探究五
11个
OA = DO = CB
变式一:与向量OA长度相等的向量
有多少个?
变式二:是否存在与向量OA长度相等,方向
相反的向量?( 相反向量)
存在,为 FE
CB、DO、FE
变式三:与向量OA长度相等的共线向量有哪些?
例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA、OB 、OC 相等的向量。
任务探究六
任务探究七
判断:
若|a|=|b|,则a=b . ( )
若a=b ,则|a|=|b|.( )
|AB|=|BA|. ( )
x
v
v
向量
定义
长度(模)
表示
几何表示法:有向线段
符号表示法:
零向量
单位向量
向量间
的关系
相等向量
平行(共线)向量
向量的有关概念
特殊向量
小结
是否存在与向量 长度相等,方向相反的向量?
与向量 长度相等的向量有几个?
如图,设O是正六边形ABCDEF的中心,分别写出图中与向量 相等的向量.
解:
思考3:
与向量 共线的向量有那些
思考1:
11个
思考2:
存在
D
E
C
A
B
F
O
长度相等方向相反
的两个向量称为相
反向量
复习回顾
复习回顾
1.向量的定义:
我们把既有大小又有方向的量叫向量.
2.向量的表示方法:
(1)用有向线段来表示。
(2)用字母来表示,或用表示向量的有向线段的起点和终点字母表示.
3.相等向量:
长度相等且方向相同的向量叫做相等向量.
4.共线向量:
方向相同或相反的非零向量叫做平行向量.平行向量也叫做共线向量.
问题1 数能进行加法运算,与数的运算类比向量能否进行加法运算呢?
解题
分析下列实例:
①飞机从广州飞往上海,再从上海飞往北京(如图),这两次位移的结果与飞机从广州直接飞往北京的位移是相同的.
广州
北京
上海
知识拓展
.
②有两条拖轮牵引一艘轮船,它们的牵引力分别是F1=3 000 N,F2=2 000 N,牵引绳之间的夹角为θ=60°(如图),如果只用一条拖轮来牵引,也能产生跟原来相同的效果
(1)从物理学的角度,上面实例中位移、牵引力说明了什么?体现了向量的什么运算?
[提示] 后面的一次位移叫前面两次位移的合位移,四边形OACB的对角线
(OC)表示的力是(OA)与(OB)表示力的合力.体现了向量的加法运算.
→
→
→
(2)上述实例中位移的和运算、力的和运算分别用什么法则?
[提示] 三角形法则和平行四边形法则.
任务探究一
知识梳理 (1)向量加法的定义:求两个向量 的运算,
叫做向量的加法,两个向量的和仍然是一个 .
(2)向量求和的法则:
向量求和法则 定义 图形表示
三角形法则 已知非零向量a,b,在平面上任取一点A,作=a,=b,则向量叫做a与b的和,记作a+b,即a+b=+=.这种求向量和的方法,称为向量加法的法则
和
向量
任务探究二
向量求和法则 定义 图形表示
平行四边形法则 已知两个不共线向量a,b,作 OA =a,OB=b,以, OA,OB为邻边作 OACB,则以O为起点的向量OC就是向量a与b的和.这种作两个向量和的方法叫做向量加法的平行四边形法则
记忆口诀 ①三角形法则:作平移,首尾连,由起点指终点.②平行四边形法则:作平移,共起点,四边形,对角线
任务探究三
向量加法的定义:
我们把求两个向量 和的运算,叫做向量的加法, 记作 .
两个向量的和是向量还是数量?
两个向量的和仍然是一个向量.
思考:
上海
香港
台北
O
A
B
问题2 上海与台北直航之前乘飞机如何从上海到达台北?
问题3直航之后可以从上海直达台北,此时的位移OB与前面两次位移OA,AB的结果有何关系?
OA+AB=OB
情景一
任务探究五
向量加法的三角形法则:
C
A
B
首尾连
首尾相接
位移的合成可以看作向量加法三角形法则的物理模型
还有没有其他的做法?
任务探究六
F1
F2
F
E
O
O
E
橡皮条在力F1与F2的作用下,从E点伸长
到了O点.同时橡皮条在力F的作用下也从E
点伸长到了O点.
问题4: 合力F与力F1、F2有怎样的关系?
F1+F2=F
力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.
任务探究七
F1
F2
F1
F2
F
F
E
O
O
E
橡皮条在力F1与F2的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸到了O点.
问题4: 合力F与力F1、F2有怎样的关系?
F1+F2=F
F是以F1与F2为邻边所形成的
平行四边形的对角线
任务探究八
例1 已知向量a,b,分别用向量加法的三角形法则与向量加法的平行四边形法则作出向量a+b
任务探究九
A
B
C
D
E
根据图示填空:
任务探究十
注意:
当向量 a 与 b 不共线时, |a+b|<|a|+|b|
C
b
a
B
A
任务探究十一
向量加法的平行四边形法则
b
a
A
a
a
a
a
a
a
b
B
b
a
D
a
C
b
a+b
共 起 点
任务探究十二
两种特例(两向量平行)
A
B
C
方向相同
方向相反
C
A
B
任务探究十三
零向量和任一向量 的和是什么
规定:
想一想
任务探究十四
b
a
b
a
+
a
b
b
a
+
b
a
c
+
a
b
+
(
)
a
+
b
c
+
(
)
,
.
a
如图,已知 , , ,请作出
b
c
a
b
+
a
b
+
c
b
+
,
,
b
a
c
c
例1:
任务探究十五
注意:
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和向量仍是一个向量.
二、 两个向量的和向量的作法:
A
B
C
1. 三角形法则:
任务探究十六
二、 两个向量的和向量的作法:
2. 平行四边形法则:
注意:平行四边形法则对于两个向量共线时不适用。
任务探究十七
向量加法的运算律
交换律:
结合律:
任务探究十八
1.化简
2.根据图示填空
A
B
D
E
C
任务探究十九
思考
使前一个向量的终点为后一个向量的起点,可以推广到n个向量相加。
(首尾相接,首尾连)
任务探究二十
例2.一艘船从A点出发以 km/h的速度向垂直于对岸的方向行驶,同时江水的流速为向东2km/h
(1)试用向量表示江水速度、船速以及船实际航行的速度(2)求船实际航行的速度的大小与方向. (用与江水速度间的夹角表示,精确到度)
分析:船实际航行速度是题中两速度的合速度.
任务探究二十一
A
B
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
(1) 同向
(2)反向
规定:
A
B
C
任务探究二十三
当向量 不共线时,和向量的长度 与向量 的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
任务探究二十四
探究
任务探究二十五
数的加法满足交换律和结合律,即对任意
那么对任意向量 的加法是否也满足交换律和结合律?
请画图进行探索。
O
A
B
C
A
C
D
任务探究二十六
例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
任务探究二十七
解:(1)
C
A
D
船速
B
水速
船实际航行速度
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
任务探究二十七
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
在Rt△ABC中,
C
A
D
B
答:船实际航行速度大小约为5.4km/h,方向与水的流速间的夹角约为68°
任务探究二十七
1.向量的加法运算:
O
A
B
三角形法则
O
A
B
C
平行四边形法则
注意:当两向量共线时,三角形法则适用,而平行四边形不再适用.
小结
比较平行四边形法则与三角形法则
平行四边形法则是从同一点出发作两个向量,以这两个向量为边作平行四边形,以同一点为起点的对角线是两向量的和。
三角形法则中两向量不是从同一点出发,而是“首尾相接”,以表示第一个向量的有向线段的终点为表示第二个向量的有向线段的起点,从第一条有向线段起点指向第二条有向线段的终点的有向线段表示两向量的和。
小结
部编版高一数学必修下第一章6.2.1
6.2 平面向量的运算
6.2.1 向量的加法运算
1.数学抽象:阅读和理解向量及向量符号的由来,理解平面向量加法运算的几何意义.
2.直观想象:借助实例和平面向量的几何意义,
3.逻辑推理: 掌握平面向量加法运算及运算规则.
4.数学运算:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
核心素养目标
教学目标
教学重点:1.借助实例和平面向量的几何意义,掌握平面向量加法运算及运算规则.
2.理解平面向量加法运算的几何意义.
3.会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.
教学难点:对平面向量加法运算的几何意义的理解.
唉, 哪儿去了
嘻嘻!大笨猫!
B
A
猫能捉住老鼠吗
老鼠由A向东北方向以10m/s的速度逃窜,而猫由B向东南方向6m/s的速度追. 问猫能否抓到老鼠
C
D
你方向错了!
情境导入
情境导入
向量最初被应用于物理学,被称为矢量。
亚里士多德是古希腊著名的科学家,他是柏拉图的学生,亚历山大的老师。大约公元前350年,亚里士多德就知道了力可以表示为向量。
任务探究一
(一)向量的物理背景与概念
1.问:力、速度、加速度、位移有什么共同特点?
向量:既有大小,又有方向的量.
向量的两要素:方向、大小
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
知识拓展
带有方向的线段叫做有向线段.
英国大科学家牛顿(Newton,1642-1727),最先使用有向线段表示向量。
1806年,瑞士人阿尔冈以
表示一个有向线段或向量。
1827年莫比乌斯(1827年)则以 表示起点为A,终点为B的向量,这用法为相当广泛的数学家所接受。
知识拓展
1912年,兰格文用 表示向量,以后,字母上加箭头表示向量的方法逐渐流行, 尤其在手写稿中。一些作者为了方便印刷,以粗黑体小写字母a,b等表示向量。这两种符号一直沿用至今。
知识拓展
(二)向量的表示
1、向量的几何表示:用有向线段表示。
有向线段的三个要素: 起点、方向、长度
向量AB的大小,也就是向量AB的长度(或称模),记作|AB|。
2、向量的字母表示:(1)a , b , c , . . .
(2)用表示向量的有向线段的起点和终点字母
表示,例如,AB,CD
知识拓展
两个特殊的向量
零向量:
长度为0的向量叫做零向量,记作 0.
注:零向量也有方向,并且规定零向量的方向是任意的
单位向量:
长度等于1个单位的向量叫做单位向量.
1.温度含零上和零下温度,所以温度是向量.( )
判断题
×
2.向量的模是一个正实数.( )
×
注:向量不能比较大小
4.若|a|>|b| ,则a 与b就能比较大小 ( )
3.若|a|=0,则a = 0 . ( )
×
×
任务探究二
任务探究三
(三)相等向量与共线向量
1.平行向量、共线向量和相等向量的概念及表示;
2.任意一组平行向量都可以平移到同一直线上吗?
3. 平行向量一定是相等向量吗?
4.相等向量一定是平行向量吗?
5.若非零向量AB//CD ,那么AB//CD吗?
平行向量又叫做共线向量
如:
a
b
c
(1)平行向量:方向相同或相反的非零向量叫做平行向量。
记作 a ∥b ∥c
规定:0与任一向量平行。
问:把一组平行于直线l的向量的起点平移到直线l上的 一点O ,这时它们是不是平行向量?
o
l
.
C
OC = c
A
OA = a
OB = b
B
(三)相等向量与共线向量
任务探究四
向量相等 向量平行
平行向量一定是相等向量吗
相等向量一定是平行向量吗
(2)相等向量:长度相等且方向相同的向量叫做相等向量。
记作:a = b
a
b
1.若非零向量AB//CD ,那么AB//CD吗?
2.若a//b ,则a与b的方向一定相同或相反吗?
o
.
b
a
注:向量可任意平行移动.
(三)相等向量与共线向量
任务探究五
11个
OA = DO = CB
变式一:与向量OA长度相等的向量
有多少个?
变式二:是否存在与向量OA长度相等,方向
相反的向量?( 相反向量)
存在,为 FE
CB、DO、FE
变式三:与向量OA长度相等的共线向量有哪些?
例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA、OB 、OC 相等的向量。
任务探究六
任务探究七
判断:
若|a|=|b|,则a=b . ( )
若a=b ,则|a|=|b|.( )
|AB|=|BA|. ( )
x
v
v
向量
定义
长度(模)
表示
几何表示法:有向线段
符号表示法:
零向量
单位向量
向量间
的关系
相等向量
平行(共线)向量
向量的有关概念
特殊向量
小结
是否存在与向量 长度相等,方向相反的向量?
与向量 长度相等的向量有几个?
如图,设O是正六边形ABCDEF的中心,分别写出图中与向量 相等的向量.
解:
思考3:
与向量 共线的向量有那些
思考1:
11个
思考2:
存在
D
E
C
A
B
F
O
长度相等方向相反
的两个向量称为相
反向量
复习回顾
复习回顾
1.向量的定义:
我们把既有大小又有方向的量叫向量.
2.向量的表示方法:
(1)用有向线段来表示。
(2)用字母来表示,或用表示向量的有向线段的起点和终点字母表示.
3.相等向量:
长度相等且方向相同的向量叫做相等向量.
4.共线向量:
方向相同或相反的非零向量叫做平行向量.平行向量也叫做共线向量.
问题1 数能进行加法运算,与数的运算类比向量能否进行加法运算呢?
解题
分析下列实例:
①飞机从广州飞往上海,再从上海飞往北京(如图),这两次位移的结果与飞机从广州直接飞往北京的位移是相同的.
广州
北京
上海
知识拓展
.
②有两条拖轮牵引一艘轮船,它们的牵引力分别是F1=3 000 N,F2=2 000 N,牵引绳之间的夹角为θ=60°(如图),如果只用一条拖轮来牵引,也能产生跟原来相同的效果
(1)从物理学的角度,上面实例中位移、牵引力说明了什么?体现了向量的什么运算?
[提示] 后面的一次位移叫前面两次位移的合位移,四边形OACB的对角线
(OC)表示的力是(OA)与(OB)表示力的合力.体现了向量的加法运算.
→
→
→
(2)上述实例中位移的和运算、力的和运算分别用什么法则?
[提示] 三角形法则和平行四边形法则.
任务探究一
知识梳理 (1)向量加法的定义:求两个向量 的运算,
叫做向量的加法,两个向量的和仍然是一个 .
(2)向量求和的法则:
向量求和法则 定义 图形表示
三角形法则 已知非零向量a,b,在平面上任取一点A,作=a,=b,则向量叫做a与b的和,记作a+b,即a+b=+=.这种求向量和的方法,称为向量加法的法则
和
向量
任务探究二
向量求和法则 定义 图形表示
平行四边形法则 已知两个不共线向量a,b,作 OA =a,OB=b,以, OA,OB为邻边作 OACB,则以O为起点的向量OC就是向量a与b的和.这种作两个向量和的方法叫做向量加法的平行四边形法则
记忆口诀 ①三角形法则:作平移,首尾连,由起点指终点.②平行四边形法则:作平移,共起点,四边形,对角线
任务探究三
向量加法的定义:
我们把求两个向量 和的运算,叫做向量的加法, 记作 .
两个向量的和是向量还是数量?
两个向量的和仍然是一个向量.
思考:
上海
香港
台北
O
A
B
问题2 上海与台北直航之前乘飞机如何从上海到达台北?
问题3直航之后可以从上海直达台北,此时的位移OB与前面两次位移OA,AB的结果有何关系?
OA+AB=OB
情景一
任务探究五
向量加法的三角形法则:
C
A
B
首尾连
首尾相接
位移的合成可以看作向量加法三角形法则的物理模型
还有没有其他的做法?
任务探究六
F1
F2
F
E
O
O
E
橡皮条在力F1与F2的作用下,从E点伸长
到了O点.同时橡皮条在力F的作用下也从E
点伸长到了O点.
问题4: 合力F与力F1、F2有怎样的关系?
F1+F2=F
力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.
任务探究七
F1
F2
F1
F2
F
F
E
O
O
E
橡皮条在力F1与F2的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸到了O点.
问题4: 合力F与力F1、F2有怎样的关系?
F1+F2=F
F是以F1与F2为邻边所形成的
平行四边形的对角线
任务探究八
例1 已知向量a,b,分别用向量加法的三角形法则与向量加法的平行四边形法则作出向量a+b
任务探究九
A
B
C
D
E
根据图示填空:
任务探究十
注意:
当向量 a 与 b 不共线时, |a+b|<|a|+|b|
C
b
a
B
A
任务探究十一
向量加法的平行四边形法则
b
a
A
a
a
a
a
a
a
b
B
b
a
D
a
C
b
a+b
共 起 点
任务探究十二
两种特例(两向量平行)
A
B
C
方向相同
方向相反
C
A
B
任务探究十三
零向量和任一向量 的和是什么
规定:
想一想
任务探究十四
b
a
b
a
+
a
b
b
a
+
b
a
c
+
a
b
+
(
)
a
+
b
c
+
(
)
,
.
a
如图,已知 , , ,请作出
b
c
a
b
+
a
b
+
c
b
+
,
,
b
a
c
c
例1:
任务探究十五
注意:
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和向量仍是一个向量.
二、 两个向量的和向量的作法:
A
B
C
1. 三角形法则:
任务探究十六
二、 两个向量的和向量的作法:
2. 平行四边形法则:
注意:平行四边形法则对于两个向量共线时不适用。
任务探究十七
向量加法的运算律
交换律:
结合律:
任务探究十八
1.化简
2.根据图示填空
A
B
D
E
C
任务探究十九
思考
使前一个向量的终点为后一个向量的起点,可以推广到n个向量相加。
(首尾相接,首尾连)
任务探究二十
例2.一艘船从A点出发以 km/h的速度向垂直于对岸的方向行驶,同时江水的流速为向东2km/h
(1)试用向量表示江水速度、船速以及船实际航行的速度(2)求船实际航行的速度的大小与方向. (用与江水速度间的夹角表示,精确到度)
分析:船实际航行速度是题中两速度的合速度.
任务探究二十一
A
B
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
E
F
K
J
如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?
D
任务探究二十二
A
B
C
(1) 同向
(2)反向
规定:
A
B
C
任务探究二十三
当向量 不共线时,和向量的长度 与向量 的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
任务探究二十四
探究
任务探究二十五
数的加法满足交换律和结合律,即对任意
那么对任意向量 的加法是否也满足交换律和结合律?
请画图进行探索。
O
A
B
C
A
C
D
任务探究二十六
例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
任务探究二十七
解:(1)
C
A
D
船速
B
水速
船实际航行速度
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
任务探究二十七
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
在Rt△ABC中,
C
A
D
B
答:船实际航行速度大小约为5.4km/h,方向与水的流速间的夹角约为68°
任务探究二十七
1.向量的加法运算:
O
A
B
三角形法则
O
A
B
C
平行四边形法则
注意:当两向量共线时,三角形法则适用,而平行四边形不再适用.
小结
比较平行四边形法则与三角形法则
平行四边形法则是从同一点出发作两个向量,以这两个向量为边作平行四边形,以同一点为起点的对角线是两向量的和。
三角形法则中两向量不是从同一点出发,而是“首尾相接”,以表示第一个向量的有向线段的终点为表示第二个向量的有向线段的起点,从第一条有向线段起点指向第二条有向线段的终点的有向线段表示两向量的和。
小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
