(课前预习讲义)数学好玩之包装的学问(知识精讲+典题精练)-2023-2024学年五年级下册数学高频考点重难点讲义(北师大版)(含解析)
文档属性
| 名称 | (课前预习讲义)数学好玩之包装的学问(知识精讲+典题精练)-2023-2024学年五年级下册数学高频考点重难点讲义(北师大版)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:07 | ||
图片预览




文档简介
数学好玩之包装的学问
1.长方体的特征
【知识点归纳】
长方体的特征:
1.长方体有6个面.有三组相对的面完全相同.一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同.
2.长方体有12条棱,相对的四条棱长度相等.按长度可分为三组,每一组有4条棱.
3.长方体有8个顶点.每个顶点连接三条棱.三条棱分别叫做长方体的长,宽,高.
4.长方体相邻的两条棱互相垂直.
2.正方体的展开图
【知识点归纳】
正方体展开图形如下情况:
3.简单的立方体切拼问题
【知识点归纳】
1.拼起来,表面积减小,因为面的数目减少.
2.剪切会增加表面积,因为面的数目增加.
3.两种方式的体积都没有发生变化.
4.长方体和正方体的表面积
【知识点归纳】
长方体表面积:六个面积之和.
公式:S=2ab+2ah+2bh.(a表示底面的长,b表示底面的宽,h表示高)
正方体表面积:六个正方形面积之和.
公式:S=6a2.(a表示棱长)
5.长方体、正方体表面积与体积计算的应用
【知识点归纳】
(1)长方体:
底面是矩形的直平行六面体,叫做长方体.
长方体的性质:六个面都是长方形,(有时有两个面是正方形);相对的面面积相等;12条棱相对的4条棱长相等;8个顶点;相交于一个顶点的三条棱的长度分别叫长、宽、高;两个面相交的边叫做棱;三条棱相交的点叫做顶点.
长方体的表面积:等于它的六个面的面积之和.
如果长方体的长、宽、高、表面积分别用a、b、h、S表示,那么:S表=2(ab+ah+bh)
长方体的体积:等于长乘以宽再乘以高.
如果把长方体的长、宽、高、体积分别用a、b、h、V表示,那么:V=abh
(2)正方体:
长宽高都相等的长方体,叫做正方体.
正方体的性质:六个面都是正方形;六个面的面积相等;有12条棱,棱长都相等;有8个顶点;正方体可以看做特殊的长方体.
正方体的表面积:六个面积之和.
如果正方体的棱长、表面积分别用a、S表示,那么:S表=6a2
正方体的体积:棱长乘以棱长再乘以棱长.
如果把正方体的棱长、体积分别用a、V表示,那么:V=a3
一.选择题(共3小题)
1.用铁皮制成长方体烟囱,求用了多少铁皮,就是求这个长方体( )
A.体积 B.六个面的面积和
C.四个面的面积和 D.五个面的面积和
2.将四个长10厘米、宽6厘米、高2厘米的长方体礼品盒用包装纸包在一起,最节约包装纸的方法是( )
A.B.C.D.
3.将4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,下面最省包装纸( )
A.B.C.D.
二.填空题(共3小题)
4.有三个同样的长方体,长宽高分别是30cm,20cm,10cm;现在把它们包成一包,最多可以节约包装纸是 cm2.
5.有两盒相同的糖,每盒长20厘米,宽15厘米,高10厘米.如果将两盒糖果包成一包,包装纸最少要 平方厘米.
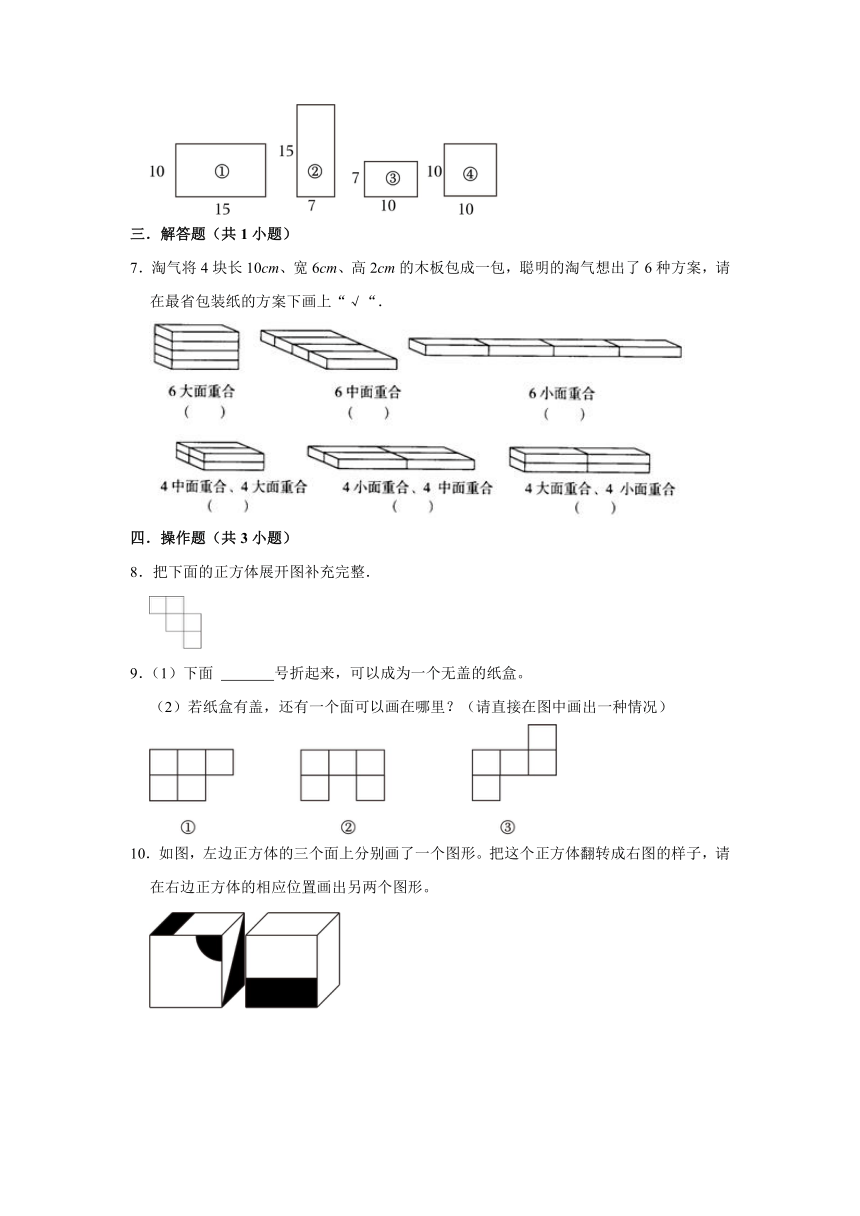
6.如图,有四种型号的塑料板各4块,若选其中的6块做一个长方体,做成的长方体共有 种可能,表面积最小是 cm2。(单位:cm)
三.解答题(共1小题)
7.淘气将4块长10cm、宽6cm、高2cm的木板包成一包,聪明的淘气想出了6种方案,请在最省包装纸的方案下画上“√“.
四.操作题(共3小题)
8.把下面的正方体展开图补充完整.
9.(1)下面 号折起来,可以成为一个无盖的纸盒。
(2)若纸盒有盖,还有一个面可以画在哪里?(请直接在图中画出一种情况)
10.如图,左边正方体的三个面上分别画了一个图形。把这个正方体翻转成右图的样子,请在右边正方体的相应位置画出另两个图形。
数学好玩之包装的学问
参考答案与试题解析
一.选择题(共3小题)
1.【答案】C
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等.由于烟囱是不需要底面的,因此,只求它的四个侧面的面积。
【解答】解:由于烟囱是不需要底面的,因此,只求它的四个侧面的面积。
故选:C。
【点评】此题主要考查出长方体的特征和表面积的计算方法,解答这类题目,首先要搞清是求哪几个面的面积,然后再根据表面积的计算方法解答。
2.【答案】A
【分析】要想更省包装纸,需使表面积最小,由题意可知:只要求出哪种情况下,拼组后的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸.据此解答即可.
【解答】解:A、表面积减少了:10×6×6
=60×6
=360(平方厘米)
B、表面积减少了:(10×6+6×2)×4
=72×4
=288(平方厘米)
C、表面积减少了:
(10×6+10×2)×4
=80×4
=320(平方厘米)
D、表面积减少了:10×2×6=120(平方厘米)
360>320>288>120
答:把这四个礼品盒的最大重合摞在一起包装最节约包装纸.
故选:A.
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用.明确:要使拼组后的表面积最小,则把最大的面相粘合.
3.【答案】B
【分析】根据长方体表面积的意义可知,把4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,要想最节省包装纸,也就是把4个长方体盒子的最大面重合摞起来进行包装。据此解答即可。
【解答】解:把4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,最节省包装纸的方法是:把4个长方体盒子的最大面重合摞起来进行包装。
故选:B。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
二.填空题(共3小题)
4.【答案】见试题解答内容
【分析】为了节省包装纸,把最大的面(30×20)重合,这样减少的4个面最大,最节约用纸.所以计算出4个长是30cm,宽是20cm的长方形的面积即可.
【解答】解;30×20×4
=600×4
=2400(平方厘米)
答:最多可以节约包装纸是2400平方厘米.
故答案为:2400.
【点评】此题解答的关键是根据长方体的表面积计算公式进行计算,要明确所需的材料最少,应减少4个最大的面.
5.【答案】见试题解答内容
【分析】要求包装纸最少用纸面积,只要找出长方体中最大的面,把两个盒面积最大的面叠在一起即可,因为20×15的面最大,这样20×15的面本来分开时是4个,叠了就变成只要算2个,其他的面还是要算4个;然后计算即可.
【解答】解:20×15×2+20×10×4+15×10×4,
=600+800+600,
=2000(平方厘米);
答:包装纸最少要2000平方厘米;
故答案为:2000.
【点评】解答此题还可以求出两个盒子的总表面积,然后减去减少的两个最大面的面积即可.
6.【答案】3,480。
【分析】通过观察图形可知,可以选择①②③各2块,做成一个长是15厘米,宽是10厘米,高是7厘米的长方体;可以选择①4块,④块,做成一个长和宽都是10厘米,高是15厘米的长方体;也可以选择③4块,④2块,做成一个长和宽都是10厘米,高是7厘米的长方体;根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出它们的表面积,然后进行比较。
【解答】解:有3种可能,
(1)选择①②③各2块,做成一个长是15厘米,宽是10厘米,高是7厘米的长方体;
(15×10+15×7+10×7)×2
=(150+105+70)×2
=325×2
=650(平方厘米)
(2)选择①4块,④2块,做成一个长和宽都是10厘米,高是15厘米的长方体;
10×10×2+15×10×4
=200+600
=800(平方厘米)
(3)选择③4块,④2块,做成一个长和宽都是10厘米,高是7厘米的长方体;
10×10×2+10×7×4
=200+280
=480(平方厘米)
480<650<800
答:有3种可能,表面积最小是480平方厘米。
故答案为:3,480。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体表面积公式的灵活运用。关键是熟记公式。
三.解答题(共1小题)
7.【答案】见试题解答内容
【分析】根据题意可知:把4块长10cm、宽6cm、高2cm的木板包成一包,要想最省包装纸,求出这6种方法减少的面的面积之和,减少面积最大的,也就是最省包装纸.据此解答即可.
【解答】解:6种方法减少的面的面积:(1)10×6×6=360(平方厘米)
(2)10×2×6=120(平方厘米)
(3)6×2×6=72(平方厘米)
(4)10×6×4+10×2×4=320(平方厘米)
(5)10×2×4+6×2×4=128(平方厘米)
(6)10×6×4+6×2×4=288(平方厘米)
第一种方法减少的面积最大,也就是把4块木板最大面重合摞在一起,这样 包装最省包装纸.
故答案为:
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用.
四.操作题(共3小题)
8.【答案】
【分析】根据正方体展开图的11种特征,可以在中间一行的右边补一个相同的正方形,变为正方体展开图的“1﹣3﹣2”型,也可在下行的右边加一个相同的正方形,变为正方体展开图的“2﹣2﹣2”型。
【解答】解:
【点评】正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
9.【答案】(1)③;
(2)(画不求唯一)。
【分析】根据正方体展开图的11种特征,①号、②号图形,在不论在哪个地方添加一个相同的正方形,都不属于正方体展开图,③号图形在中间3个正方形的左边或边添加一个相同的正方形,属于正方体展开图的“1﹣4﹣1”型,即③号图形可以折成一个无盖的正方体纸盒。
【解答】解:(1)下面③号折起来,可以成为一个无盖的纸盒。
(2)根据题画图如下(画法不唯一):
故答案为:③。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
10.【答案】
【分析】先把左面的正方体向前翻转,此时扇形在底面,圆心在右下角;长方形在前面,靠左面;三角形仍在右面,直角顶点在右上角。再向左翻转,此时长方形仍在前面,靠下面;扇形在右面,圆心在左上角;三角形在上面,直角顶点在左上角。
【解答】解:
【点评】此题考查了空间想象能力。可动手看作一下,以验证画图是否正确。
1.长方体的特征
【知识点归纳】
长方体的特征:
1.长方体有6个面.有三组相对的面完全相同.一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同.
2.长方体有12条棱,相对的四条棱长度相等.按长度可分为三组,每一组有4条棱.
3.长方体有8个顶点.每个顶点连接三条棱.三条棱分别叫做长方体的长,宽,高.
4.长方体相邻的两条棱互相垂直.
2.正方体的展开图
【知识点归纳】
正方体展开图形如下情况:
3.简单的立方体切拼问题
【知识点归纳】
1.拼起来,表面积减小,因为面的数目减少.
2.剪切会增加表面积,因为面的数目增加.
3.两种方式的体积都没有发生变化.
4.长方体和正方体的表面积
【知识点归纳】
长方体表面积:六个面积之和.
公式:S=2ab+2ah+2bh.(a表示底面的长,b表示底面的宽,h表示高)
正方体表面积:六个正方形面积之和.
公式:S=6a2.(a表示棱长)
5.长方体、正方体表面积与体积计算的应用
【知识点归纳】
(1)长方体:
底面是矩形的直平行六面体,叫做长方体.
长方体的性质:六个面都是长方形,(有时有两个面是正方形);相对的面面积相等;12条棱相对的4条棱长相等;8个顶点;相交于一个顶点的三条棱的长度分别叫长、宽、高;两个面相交的边叫做棱;三条棱相交的点叫做顶点.
长方体的表面积:等于它的六个面的面积之和.
如果长方体的长、宽、高、表面积分别用a、b、h、S表示,那么:S表=2(ab+ah+bh)
长方体的体积:等于长乘以宽再乘以高.
如果把长方体的长、宽、高、体积分别用a、b、h、V表示,那么:V=abh
(2)正方体:
长宽高都相等的长方体,叫做正方体.
正方体的性质:六个面都是正方形;六个面的面积相等;有12条棱,棱长都相等;有8个顶点;正方体可以看做特殊的长方体.
正方体的表面积:六个面积之和.
如果正方体的棱长、表面积分别用a、S表示,那么:S表=6a2
正方体的体积:棱长乘以棱长再乘以棱长.
如果把正方体的棱长、体积分别用a、V表示,那么:V=a3
一.选择题(共3小题)
1.用铁皮制成长方体烟囱,求用了多少铁皮,就是求这个长方体( )
A.体积 B.六个面的面积和
C.四个面的面积和 D.五个面的面积和
2.将四个长10厘米、宽6厘米、高2厘米的长方体礼品盒用包装纸包在一起,最节约包装纸的方法是( )
A.B.C.D.
3.将4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,下面最省包装纸( )
A.B.C.D.
二.填空题(共3小题)
4.有三个同样的长方体,长宽高分别是30cm,20cm,10cm;现在把它们包成一包,最多可以节约包装纸是 cm2.
5.有两盒相同的糖,每盒长20厘米,宽15厘米,高10厘米.如果将两盒糖果包成一包,包装纸最少要 平方厘米.
6.如图,有四种型号的塑料板各4块,若选其中的6块做一个长方体,做成的长方体共有 种可能,表面积最小是 cm2。(单位:cm)
三.解答题(共1小题)
7.淘气将4块长10cm、宽6cm、高2cm的木板包成一包,聪明的淘气想出了6种方案,请在最省包装纸的方案下画上“√“.
四.操作题(共3小题)
8.把下面的正方体展开图补充完整.
9.(1)下面 号折起来,可以成为一个无盖的纸盒。
(2)若纸盒有盖,还有一个面可以画在哪里?(请直接在图中画出一种情况)
10.如图,左边正方体的三个面上分别画了一个图形。把这个正方体翻转成右图的样子,请在右边正方体的相应位置画出另两个图形。
数学好玩之包装的学问
参考答案与试题解析
一.选择题(共3小题)
1.【答案】C
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等.由于烟囱是不需要底面的,因此,只求它的四个侧面的面积。
【解答】解:由于烟囱是不需要底面的,因此,只求它的四个侧面的面积。
故选:C。
【点评】此题主要考查出长方体的特征和表面积的计算方法,解答这类题目,首先要搞清是求哪几个面的面积,然后再根据表面积的计算方法解答。
2.【答案】A
【分析】要想更省包装纸,需使表面积最小,由题意可知:只要求出哪种情况下,拼组后的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸.据此解答即可.
【解答】解:A、表面积减少了:10×6×6
=60×6
=360(平方厘米)
B、表面积减少了:(10×6+6×2)×4
=72×4
=288(平方厘米)
C、表面积减少了:
(10×6+10×2)×4
=80×4
=320(平方厘米)
D、表面积减少了:10×2×6=120(平方厘米)
360>320>288>120
答:把这四个礼品盒的最大重合摞在一起包装最节约包装纸.
故选:A.
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用.明确:要使拼组后的表面积最小,则把最大的面相粘合.
3.【答案】B
【分析】根据长方体表面积的意义可知,把4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,要想最节省包装纸,也就是把4个长方体盒子的最大面重合摞起来进行包装。据此解答即可。
【解答】解:把4个长12cm、宽8cm、高5cm的长方体盒子用彩纸包在一起,最节省包装纸的方法是:把4个长方体盒子的最大面重合摞起来进行包装。
故选:B。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
二.填空题(共3小题)
4.【答案】见试题解答内容
【分析】为了节省包装纸,把最大的面(30×20)重合,这样减少的4个面最大,最节约用纸.所以计算出4个长是30cm,宽是20cm的长方形的面积即可.
【解答】解;30×20×4
=600×4
=2400(平方厘米)
答:最多可以节约包装纸是2400平方厘米.
故答案为:2400.
【点评】此题解答的关键是根据长方体的表面积计算公式进行计算,要明确所需的材料最少,应减少4个最大的面.
5.【答案】见试题解答内容
【分析】要求包装纸最少用纸面积,只要找出长方体中最大的面,把两个盒面积最大的面叠在一起即可,因为20×15的面最大,这样20×15的面本来分开时是4个,叠了就变成只要算2个,其他的面还是要算4个;然后计算即可.
【解答】解:20×15×2+20×10×4+15×10×4,
=600+800+600,
=2000(平方厘米);
答:包装纸最少要2000平方厘米;
故答案为:2000.
【点评】解答此题还可以求出两个盒子的总表面积,然后减去减少的两个最大面的面积即可.
6.【答案】3,480。
【分析】通过观察图形可知,可以选择①②③各2块,做成一个长是15厘米,宽是10厘米,高是7厘米的长方体;可以选择①4块,④块,做成一个长和宽都是10厘米,高是15厘米的长方体;也可以选择③4块,④2块,做成一个长和宽都是10厘米,高是7厘米的长方体;根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出它们的表面积,然后进行比较。
【解答】解:有3种可能,
(1)选择①②③各2块,做成一个长是15厘米,宽是10厘米,高是7厘米的长方体;
(15×10+15×7+10×7)×2
=(150+105+70)×2
=325×2
=650(平方厘米)
(2)选择①4块,④2块,做成一个长和宽都是10厘米,高是15厘米的长方体;
10×10×2+15×10×4
=200+600
=800(平方厘米)
(3)选择③4块,④2块,做成一个长和宽都是10厘米,高是7厘米的长方体;
10×10×2+10×7×4
=200+280
=480(平方厘米)
480<650<800
答:有3种可能,表面积最小是480平方厘米。
故答案为:3,480。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体表面积公式的灵活运用。关键是熟记公式。
三.解答题(共1小题)
7.【答案】见试题解答内容
【分析】根据题意可知:把4块长10cm、宽6cm、高2cm的木板包成一包,要想最省包装纸,求出这6种方法减少的面的面积之和,减少面积最大的,也就是最省包装纸.据此解答即可.
【解答】解:6种方法减少的面的面积:(1)10×6×6=360(平方厘米)
(2)10×2×6=120(平方厘米)
(3)6×2×6=72(平方厘米)
(4)10×6×4+10×2×4=320(平方厘米)
(5)10×2×4+6×2×4=128(平方厘米)
(6)10×6×4+6×2×4=288(平方厘米)
第一种方法减少的面积最大,也就是把4块木板最大面重合摞在一起,这样 包装最省包装纸.
故答案为:
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用.
四.操作题(共3小题)
8.【答案】
【分析】根据正方体展开图的11种特征,可以在中间一行的右边补一个相同的正方形,变为正方体展开图的“1﹣3﹣2”型,也可在下行的右边加一个相同的正方形,变为正方体展开图的“2﹣2﹣2”型。
【解答】解:
【点评】正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
9.【答案】(1)③;
(2)(画不求唯一)。
【分析】根据正方体展开图的11种特征,①号、②号图形,在不论在哪个地方添加一个相同的正方形,都不属于正方体展开图,③号图形在中间3个正方形的左边或边添加一个相同的正方形,属于正方体展开图的“1﹣4﹣1”型,即③号图形可以折成一个无盖的正方体纸盒。
【解答】解:(1)下面③号折起来,可以成为一个无盖的纸盒。
(2)根据题画图如下(画法不唯一):
故答案为:③。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
10.【答案】
【分析】先把左面的正方体向前翻转,此时扇形在底面,圆心在右下角;长方形在前面,靠左面;三角形仍在右面,直角顶点在右上角。再向左翻转,此时长方形仍在前面,靠下面;扇形在右面,圆心在左上角;三角形在上面,直角顶点在左上角。
【解答】解:
【点评】此题考查了空间想象能力。可动手看作一下,以验证画图是否正确。
