第二单元《长方体(一)》(同步练习)-2023-2024学年五年级下册数学北师大版(含答案)
文档属性
| 名称 | 第二单元《长方体(一)》(同步练习)-2023-2024学年五年级下册数学北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 201.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 15:06:59 | ||
图片预览


文档简介
北师大版数学五年级下第二单元《长方体(一)》复习试题
一.选择题(共15小题)
1.有一根铁丝,恰好可以围成长6厘米、宽3厘米、高3厘米的长方体框架,这根铁丝恰好也可以围成一个正方体框架,则围成的正方体框架的棱长是( )厘米。
A.1 B.4 C.8 D.16
2.一个长方体长5m,宽4m,高3m,如果截成一个最大的正方体。这个正方体的底面积是( )m2。
A.25 B.16 C.9 D.15
3.有若干根10厘米和8厘米长的小棒和若干团橡皮泥团,小强想做一个长和宽都是8厘米,高是10厘米的长方体框架,需要8厘米的小棒( )根。
A.4 B.6 C.8 D.12
4.如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与( )点重合。
A.B B.C C.D D.E
5.下列选项中,不是正方体展开图的是( )
A. B. C. D.
6.如图所示是一个正方体的展开图,图中每个面上均写有一个数字,把这个图形折叠成正方体后,相对的面上的两个数之积最大是( )
A.8 B.15 C.18 D.24
7.一个长方体被挖掉一小块,如图,下面说法完全正确的是( )
A.体积减少,表面积也减少
B.体积减少,表面积增加
C.体积减少,表面积不变
D.体积不变,表面积不变
8.一个长方体,长6厘米,宽4厘米,高3厘米,它的最小面的面积与表面积的比是( )
A.l:3 B.1:9 C.l:12 D.l:24
9.(如图)把两个棱长为4厘米的正方体木块和一个长16厘米,宽8厘米,高8厘米的长方体木块粘贴在一起,那么粘贴后的表面积比原来三个木块表面积之和减少( )平方厘米。
A.16 B.32 C.64 D.96
10.把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加( )平方厘米。
A.480 B.160 C.96 D.80
11.将四个完全一样的长方体盒子包成一包,长方体的长是15厘米,宽是8厘米,高是1厘米。下面四种包装中,( )种方式最省包装纸。
A. B. C. D.
12.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
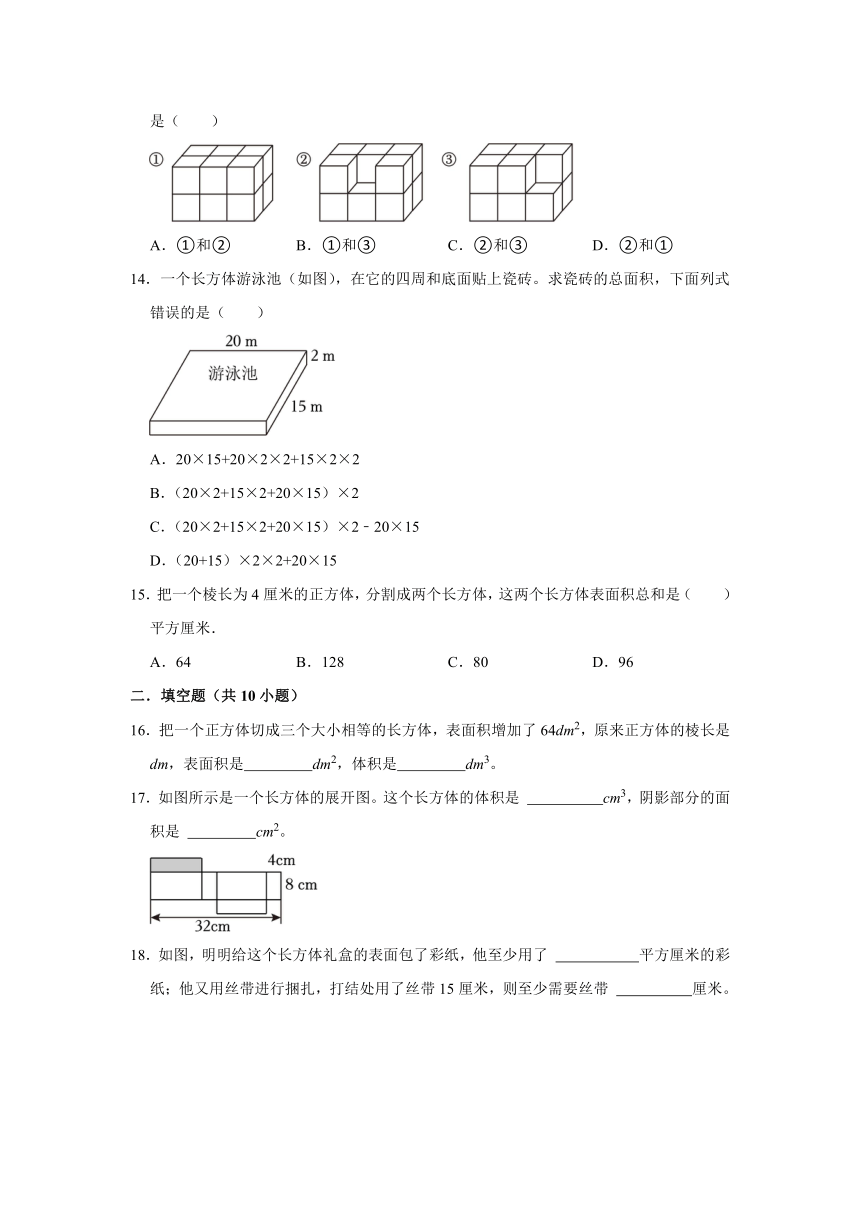
13.如图形都是以棱长1cm的小正方体堆积而成,其中,体积最大的和表面积最大的分别是( )
A.①和② B.①和③ C.②和③ D.②和①
14.一个长方体游泳池(如图),在它的四周和底面贴上瓷砖。求瓷砖的总面积,下面列式错误的是( )
A.20×15+20×2×2+15×2×2
B.(20×2+15×2+20×15)×2
C.(20×2+15×2+20×15)×2﹣20×15
D.(20+15)×2×2+20×15
15.把一个棱长为4厘米的正方体,分割成两个长方体,这两个长方体表面积总和是( )平方厘米.
A.64 B.128 C.80 D.96
二.填空题(共10小题)
16.把一个正方体切成三个大小相等的长方体,表面积增加了64dm2,原来正方体的棱长是 dm,表面积是 dm2,体积是 dm3。
17.如图所示是一个长方体的展开图。这个长方体的体积是 cm3,阴影部分的面积是 cm2。
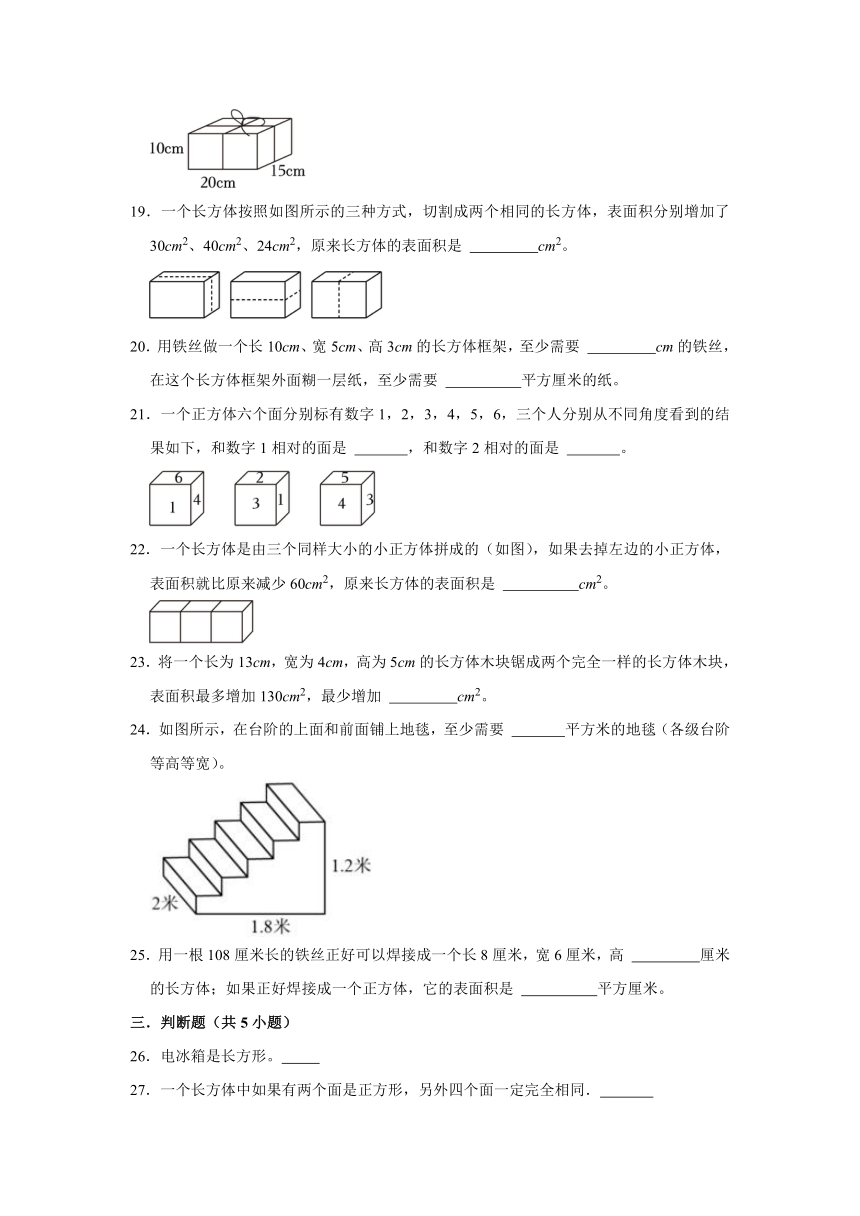
18.如图,明明给这个长方体礼盒的表面包了彩纸,他至少用了 平方厘米的彩纸;他又用丝带进行捆扎,打结处用了丝带15厘米,则至少需要丝带 厘米。
19.一个长方体按照如图所示的三种方式,切割成两个相同的长方体,表面积分别增加了30cm2、40cm2、24cm2,原来长方体的表面积是 cm2。
20.用铁丝做一个长10cm、宽5cm、高3cm的长方体框架,至少需要 cm的铁丝,在这个长方体框架外面糊一层纸,至少需要 平方厘米的纸。
21.一个正方体六个面分别标有数字1,2,3,4,5,6,三个人分别从不同角度看到的结果如下,和数字1相对的面是 ,和数字2相对的面是 。
22.一个长方体是由三个同样大小的小正方体拼成的(如图),如果去掉左边的小正方体,表面积就比原来减少60cm2,原来长方体的表面积是 cm2。
23.将一个长为13cm,宽为4cm,高为5cm的长方体木块锯成两个完全一样的长方体木块,表面积最多增加130cm2,最少增加 cm2。
24.如图所示,在台阶的上面和前面铺上地毯,至少需要 平方米的地毯(各级台阶等高等宽)。
25.用一根108厘米长的铁丝正好可以焊接成一个长8厘米,宽6厘米,高 厘米的长方体;如果正好焊接成一个正方体,它的表面积是 平方厘米。
三.判断题(共5小题)
26.电冰箱是长方形。
27.一个长方体中如果有两个面是正方形,另外四个面一定完全相同.
28.长方体相邻两个面的面积一定不相等. .
29.正方体的棱长扩大到原来的2倍,表面积和体积都扩大到原来的8倍。
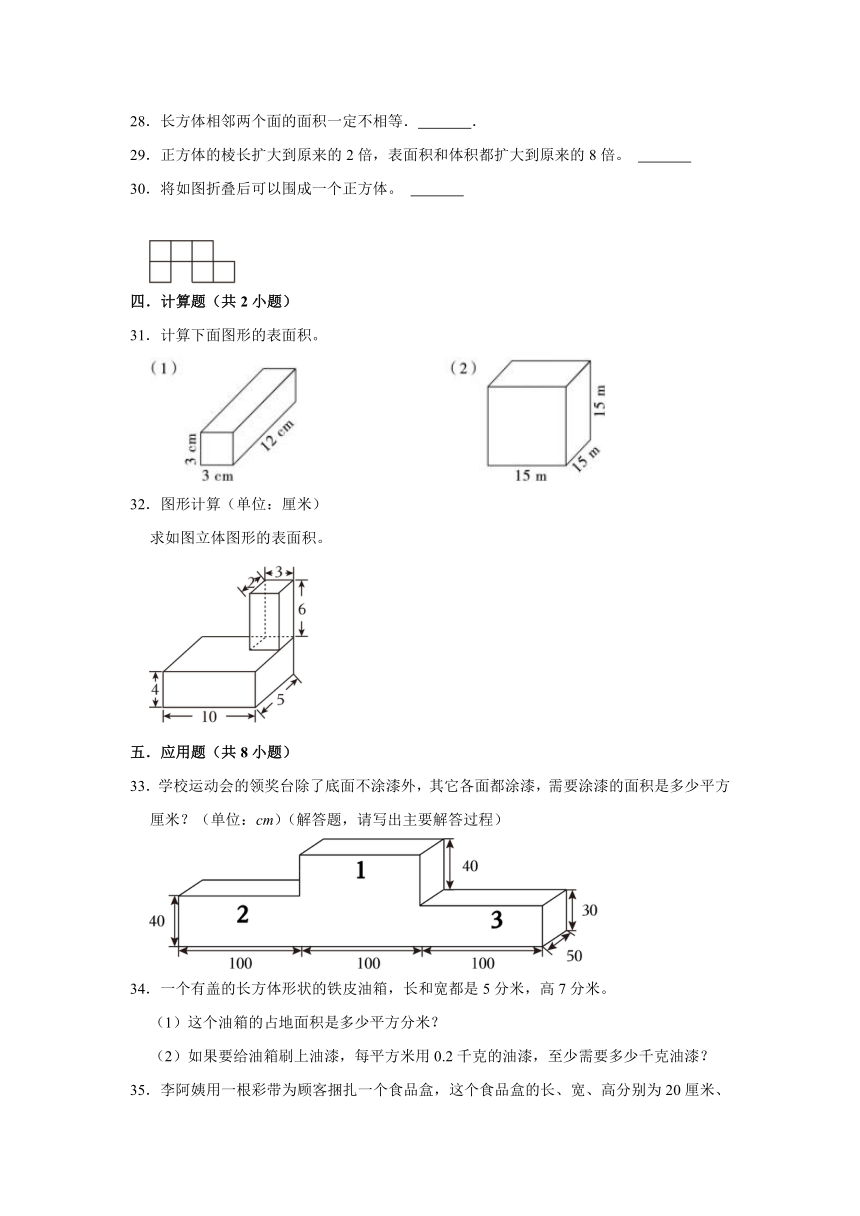
30.将如图折叠后可以围成一个正方体。
四.计算题(共2小题)
31.计算下面图形的表面积。
32.图形计算(单位:厘米)
求如图立体图形的表面积。
五.应用题(共8小题)
33.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
34.一个有盖的长方体形状的铁皮油箱,长和宽都是5分米,高7分米。
(1)这个油箱的占地面积是多少平方分米?
(2)如果要给油箱刷上油漆,每平方米用0.2千克的油漆,至少需要多少千克油漆?
35.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
36.7个棱长为5dm的正方体纸箱放在墙角(如下图),露在外面的面积是多少平方分米?
37.一个长方体(如图),如果高增加3厘米,就变成了棱长是10厘米的正方体,表面积和体积各增加了多少?
38.将8个棱长为2厘米的小正方体礼盒包装成一个大礼盒,包装纸至少要多少平方厘米?(先想一想,画出草图,再解答)
39.一个长方体饼干盒,长20cm、宽15cm、高30cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少要多少平方厘米?
40.学校电脑室长9m,宽7m,高3m。
(1)要给电脑室的地面铺上地砖,铺地砖的面积是多少m2?
(2)现在粉刷电脑室屋顶和四壁,扣除门窗和黑板的面积18m2,粉刷的面积是多少m2?
参考答案
一.选择题(共15小题)
1.B。
2.C。
3.C。
4.C。
5.D。
6.C。
7.C。
8.B.
9.C。
10.B。
11.C。
12.C。
13.A。
14.B。
15B.
二.填空题(共10小题)
16.把一个正方体切成三个大小相等的长方体,表面积增加了64dm2,原来正方体的棱长是 4 dm,表面积是 96 dm2,体积是 64 dm3。
17.如图所示是一个长方体的展开图。这个长方体的体积是 384 cm3,阴影部分的面积是 48 cm2。
18.如图,明明给这个长方体礼盒的表面包了彩纸,他至少用了 1300 平方厘米的彩纸;他又用丝带进行捆扎,打结处用了丝带15厘米,则至少需要丝带 125 厘米。
19.一个长方体按照如图所示的三种方式,切割成两个相同的长方体,表面积分别增加了30cm2、40cm2、24cm2,原来长方体的表面积是 94 cm2。
20.用铁丝做一个长10cm、宽5cm、高3cm的长方体框架,至少需要 72 cm的铁丝,在这个长方体框架外面糊一层纸,至少需要 190 平方厘米的纸。
21.一个正方体六个面分别标有数字1,2,3,4,5,6,三个人分别从不同角度看到的结果如下,和数字1相对的面是 5 ,和数字2相对的面是 4 。
22.一个长方体是由三个同样大小的小正方体拼成的(如图),如果去掉左边的小正方体,表面积就比原来减少60cm2,原来长方体的表面积是 210 cm2。
23.将一个长为13cm,宽为4cm,高为5cm的长方体木块锯成两个完全一样的长方体木块,表面积最多增加130cm2,最少增加 40 cm2。
24.如图所示,在台阶的上面和前面铺上地毯,至少需要 6 平方米的地毯(各级台阶等高等宽)。
25.用一根108厘米长的铁丝正好可以焊接成一个长8厘米,宽6厘米,高 13 厘米的长方体;如果正好焊接成一个正方体,它的表面积是 486 平方厘米。
三.判断题(共5小题)
26.电冰箱是长方形。 ×
27.一个长方体中如果有两个面是正方形,另外四个面一定完全相同. √
28.长方体相邻两个面的面积一定不相等. × .
29.正方体的棱长扩大到原来的2倍,表面积和体积都扩大到原来的8倍。 ×
30.将如图折叠后可以围成一个正方体。 ×
四.计算题(共2小题)
31.计算下面图形的表面积。
解:(1)(12×3+12×3+3×3)×2
=(36+36+9)×2
=81×2
=162(平方厘米)
答:它的表面积是162平方厘米。
(2)15×15×6
=225×6
=1350(平方米)
答:它的表面积是1350平方米。
32.图形计算(单位:厘米)
求如图立体图形的表面积。
解:大长方体的表面积=(4×10+4×5+10×5)×2
=(40+20+50)×2
=110×2
=220(平方厘米)
小长方体的四个侧面的表面积=(6×3+6×2)×2
=(18+12)×2
=30×2
=60(平方厘米)
220+60=280(平方厘米)
答:立体图形的表面积是280平方厘米。
五.应用题(共8小题)
33.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
解:(1)40×100×2+40×50+100×50×3+(40+30)×100×2+40×50+(40+30﹣40)×50+100×30×2+50×30
=8000+2000+15000+14000+2000+1500+6000+1500
=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米.
34.一个有盖的长方体形状的铁皮油箱,长和宽都是5分米,高7分米。
(1)这个油箱的占地面积是多少平方分米?
(2)如果要给油箱刷上油漆,每平方米用0.2千克的油漆,至少需要多少千克油漆?
解:(1)5×5=25(平方分米)
答:这个油箱的占地面积是25平方分米。
(2)(5×5+5×7+5×7)×2
=(25+35+35)×2
=95×2
=190(平方分米)
190平方分米=1.9平方米
1.9×0.2=0.38(千克)
答:至少需要0.38千克油漆。
35.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
解:20×4+10×4+5×4+20
=80+40+20+20
=160(厘米)
160厘米=16分米
答:这样一共需要16分米长的彩带。
36.7个棱长为5dm的正方体纸箱放在墙角(如下图),露在外面的面积是多少平方分米?
解:3×4=12(个)
5×5×12
=25×12
=300(平方分米)
答:露在外面的面积是300平方分米。
37.一个长方体(如图),如果高增加3厘米,就变成了棱长是10厘米的正方体,表面积和体积各增加了多少?
解:10×3×4=120(平方厘米)
10×10×3=300(立方厘米)
答:表面积增加了120平方厘米,体积增加了300 立方厘米。
38.将8个棱长为2厘米的小正方体礼盒包装成一个大礼盒,包装纸至少要多少平方厘米?(先想一想,画出草图,再解答)
解:
大正方体棱长:2×2=4(厘米)
表面积:4×4×6
=16×6
=96(平方厘米)
答:包装纸至少要96平方厘米。
39.一个长方体饼干盒,长20cm、宽15cm、高30cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少要多少平方厘米?
解:(20×30+15×30)×2
=(600+450)×2
=1050×2
=2100(平方厘米)
答:这张商标纸的面积至少要2100平方厘米。
40.学校电脑室长9m,宽7m,高3m。
(1)要给电脑室的地面铺上地砖,铺地砖的面积是多少m2?
(2)现在粉刷电脑室屋顶和四壁,扣除门窗和黑板的面积18m2,粉刷的面积是多少m2?
(1)9×7=63(m2)
答:铺地砖的面积是63m2。
(2)9×7+7×3×2+9×3×2﹣18
=63+42+54﹣18
=159﹣18
=141(m2)
答:粉刷的面积是141m2。
一.选择题(共15小题)
1.有一根铁丝,恰好可以围成长6厘米、宽3厘米、高3厘米的长方体框架,这根铁丝恰好也可以围成一个正方体框架,则围成的正方体框架的棱长是( )厘米。
A.1 B.4 C.8 D.16
2.一个长方体长5m,宽4m,高3m,如果截成一个最大的正方体。这个正方体的底面积是( )m2。
A.25 B.16 C.9 D.15
3.有若干根10厘米和8厘米长的小棒和若干团橡皮泥团,小强想做一个长和宽都是8厘米,高是10厘米的长方体框架,需要8厘米的小棒( )根。
A.4 B.6 C.8 D.12
4.如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与( )点重合。
A.B B.C C.D D.E
5.下列选项中,不是正方体展开图的是( )
A. B. C. D.
6.如图所示是一个正方体的展开图,图中每个面上均写有一个数字,把这个图形折叠成正方体后,相对的面上的两个数之积最大是( )
A.8 B.15 C.18 D.24
7.一个长方体被挖掉一小块,如图,下面说法完全正确的是( )
A.体积减少,表面积也减少
B.体积减少,表面积增加
C.体积减少,表面积不变
D.体积不变,表面积不变
8.一个长方体,长6厘米,宽4厘米,高3厘米,它的最小面的面积与表面积的比是( )
A.l:3 B.1:9 C.l:12 D.l:24
9.(如图)把两个棱长为4厘米的正方体木块和一个长16厘米,宽8厘米,高8厘米的长方体木块粘贴在一起,那么粘贴后的表面积比原来三个木块表面积之和减少( )平方厘米。
A.16 B.32 C.64 D.96
10.把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加( )平方厘米。
A.480 B.160 C.96 D.80
11.将四个完全一样的长方体盒子包成一包,长方体的长是15厘米,宽是8厘米,高是1厘米。下面四种包装中,( )种方式最省包装纸。
A. B. C. D.
12.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
13.如图形都是以棱长1cm的小正方体堆积而成,其中,体积最大的和表面积最大的分别是( )
A.①和② B.①和③ C.②和③ D.②和①
14.一个长方体游泳池(如图),在它的四周和底面贴上瓷砖。求瓷砖的总面积,下面列式错误的是( )
A.20×15+20×2×2+15×2×2
B.(20×2+15×2+20×15)×2
C.(20×2+15×2+20×15)×2﹣20×15
D.(20+15)×2×2+20×15
15.把一个棱长为4厘米的正方体,分割成两个长方体,这两个长方体表面积总和是( )平方厘米.
A.64 B.128 C.80 D.96
二.填空题(共10小题)
16.把一个正方体切成三个大小相等的长方体,表面积增加了64dm2,原来正方体的棱长是 dm,表面积是 dm2,体积是 dm3。
17.如图所示是一个长方体的展开图。这个长方体的体积是 cm3,阴影部分的面积是 cm2。
18.如图,明明给这个长方体礼盒的表面包了彩纸,他至少用了 平方厘米的彩纸;他又用丝带进行捆扎,打结处用了丝带15厘米,则至少需要丝带 厘米。
19.一个长方体按照如图所示的三种方式,切割成两个相同的长方体,表面积分别增加了30cm2、40cm2、24cm2,原来长方体的表面积是 cm2。
20.用铁丝做一个长10cm、宽5cm、高3cm的长方体框架,至少需要 cm的铁丝,在这个长方体框架外面糊一层纸,至少需要 平方厘米的纸。
21.一个正方体六个面分别标有数字1,2,3,4,5,6,三个人分别从不同角度看到的结果如下,和数字1相对的面是 ,和数字2相对的面是 。
22.一个长方体是由三个同样大小的小正方体拼成的(如图),如果去掉左边的小正方体,表面积就比原来减少60cm2,原来长方体的表面积是 cm2。
23.将一个长为13cm,宽为4cm,高为5cm的长方体木块锯成两个完全一样的长方体木块,表面积最多增加130cm2,最少增加 cm2。
24.如图所示,在台阶的上面和前面铺上地毯,至少需要 平方米的地毯(各级台阶等高等宽)。
25.用一根108厘米长的铁丝正好可以焊接成一个长8厘米,宽6厘米,高 厘米的长方体;如果正好焊接成一个正方体,它的表面积是 平方厘米。
三.判断题(共5小题)
26.电冰箱是长方形。
27.一个长方体中如果有两个面是正方形,另外四个面一定完全相同.
28.长方体相邻两个面的面积一定不相等. .
29.正方体的棱长扩大到原来的2倍,表面积和体积都扩大到原来的8倍。
30.将如图折叠后可以围成一个正方体。
四.计算题(共2小题)
31.计算下面图形的表面积。
32.图形计算(单位:厘米)
求如图立体图形的表面积。
五.应用题(共8小题)
33.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
34.一个有盖的长方体形状的铁皮油箱,长和宽都是5分米,高7分米。
(1)这个油箱的占地面积是多少平方分米?
(2)如果要给油箱刷上油漆,每平方米用0.2千克的油漆,至少需要多少千克油漆?
35.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
36.7个棱长为5dm的正方体纸箱放在墙角(如下图),露在外面的面积是多少平方分米?
37.一个长方体(如图),如果高增加3厘米,就变成了棱长是10厘米的正方体,表面积和体积各增加了多少?
38.将8个棱长为2厘米的小正方体礼盒包装成一个大礼盒,包装纸至少要多少平方厘米?(先想一想,画出草图,再解答)
39.一个长方体饼干盒,长20cm、宽15cm、高30cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少要多少平方厘米?
40.学校电脑室长9m,宽7m,高3m。
(1)要给电脑室的地面铺上地砖,铺地砖的面积是多少m2?
(2)现在粉刷电脑室屋顶和四壁,扣除门窗和黑板的面积18m2,粉刷的面积是多少m2?
参考答案
一.选择题(共15小题)
1.B。
2.C。
3.C。
4.C。
5.D。
6.C。
7.C。
8.B.
9.C。
10.B。
11.C。
12.C。
13.A。
14.B。
15B.
二.填空题(共10小题)
16.把一个正方体切成三个大小相等的长方体,表面积增加了64dm2,原来正方体的棱长是 4 dm,表面积是 96 dm2,体积是 64 dm3。
17.如图所示是一个长方体的展开图。这个长方体的体积是 384 cm3,阴影部分的面积是 48 cm2。
18.如图,明明给这个长方体礼盒的表面包了彩纸,他至少用了 1300 平方厘米的彩纸;他又用丝带进行捆扎,打结处用了丝带15厘米,则至少需要丝带 125 厘米。
19.一个长方体按照如图所示的三种方式,切割成两个相同的长方体,表面积分别增加了30cm2、40cm2、24cm2,原来长方体的表面积是 94 cm2。
20.用铁丝做一个长10cm、宽5cm、高3cm的长方体框架,至少需要 72 cm的铁丝,在这个长方体框架外面糊一层纸,至少需要 190 平方厘米的纸。
21.一个正方体六个面分别标有数字1,2,3,4,5,6,三个人分别从不同角度看到的结果如下,和数字1相对的面是 5 ,和数字2相对的面是 4 。
22.一个长方体是由三个同样大小的小正方体拼成的(如图),如果去掉左边的小正方体,表面积就比原来减少60cm2,原来长方体的表面积是 210 cm2。
23.将一个长为13cm,宽为4cm,高为5cm的长方体木块锯成两个完全一样的长方体木块,表面积最多增加130cm2,最少增加 40 cm2。
24.如图所示,在台阶的上面和前面铺上地毯,至少需要 6 平方米的地毯(各级台阶等高等宽)。
25.用一根108厘米长的铁丝正好可以焊接成一个长8厘米,宽6厘米,高 13 厘米的长方体;如果正好焊接成一个正方体,它的表面积是 486 平方厘米。
三.判断题(共5小题)
26.电冰箱是长方形。 ×
27.一个长方体中如果有两个面是正方形,另外四个面一定完全相同. √
28.长方体相邻两个面的面积一定不相等. × .
29.正方体的棱长扩大到原来的2倍,表面积和体积都扩大到原来的8倍。 ×
30.将如图折叠后可以围成一个正方体。 ×
四.计算题(共2小题)
31.计算下面图形的表面积。
解:(1)(12×3+12×3+3×3)×2
=(36+36+9)×2
=81×2
=162(平方厘米)
答:它的表面积是162平方厘米。
(2)15×15×6
=225×6
=1350(平方米)
答:它的表面积是1350平方米。
32.图形计算(单位:厘米)
求如图立体图形的表面积。
解:大长方体的表面积=(4×10+4×5+10×5)×2
=(40+20+50)×2
=110×2
=220(平方厘米)
小长方体的四个侧面的表面积=(6×3+6×2)×2
=(18+12)×2
=30×2
=60(平方厘米)
220+60=280(平方厘米)
答:立体图形的表面积是280平方厘米。
五.应用题(共8小题)
33.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
解:(1)40×100×2+40×50+100×50×3+(40+30)×100×2+40×50+(40+30﹣40)×50+100×30×2+50×30
=8000+2000+15000+14000+2000+1500+6000+1500
=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米.
34.一个有盖的长方体形状的铁皮油箱,长和宽都是5分米,高7分米。
(1)这个油箱的占地面积是多少平方分米?
(2)如果要给油箱刷上油漆,每平方米用0.2千克的油漆,至少需要多少千克油漆?
解:(1)5×5=25(平方分米)
答:这个油箱的占地面积是25平方分米。
(2)(5×5+5×7+5×7)×2
=(25+35+35)×2
=95×2
=190(平方分米)
190平方分米=1.9平方米
1.9×0.2=0.38(千克)
答:至少需要0.38千克油漆。
35.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
解:20×4+10×4+5×4+20
=80+40+20+20
=160(厘米)
160厘米=16分米
答:这样一共需要16分米长的彩带。
36.7个棱长为5dm的正方体纸箱放在墙角(如下图),露在外面的面积是多少平方分米?
解:3×4=12(个)
5×5×12
=25×12
=300(平方分米)
答:露在外面的面积是300平方分米。
37.一个长方体(如图),如果高增加3厘米,就变成了棱长是10厘米的正方体,表面积和体积各增加了多少?
解:10×3×4=120(平方厘米)
10×10×3=300(立方厘米)
答:表面积增加了120平方厘米,体积增加了300 立方厘米。
38.将8个棱长为2厘米的小正方体礼盒包装成一个大礼盒,包装纸至少要多少平方厘米?(先想一想,画出草图,再解答)
解:
大正方体棱长:2×2=4(厘米)
表面积:4×4×6
=16×6
=96(平方厘米)
答:包装纸至少要96平方厘米。
39.一个长方体饼干盒,长20cm、宽15cm、高30cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少要多少平方厘米?
解:(20×30+15×30)×2
=(600+450)×2
=1050×2
=2100(平方厘米)
答:这张商标纸的面积至少要2100平方厘米。
40.学校电脑室长9m,宽7m,高3m。
(1)要给电脑室的地面铺上地砖,铺地砖的面积是多少m2?
(2)现在粉刷电脑室屋顶和四壁,扣除门窗和黑板的面积18m2,粉刷的面积是多少m2?
(1)9×7=63(m2)
答:铺地砖的面积是63m2。
(2)9×7+7×3×2+9×3×2﹣18
=63+42+54﹣18
=159﹣18
=141(m2)
答:粉刷的面积是141m2。
