【学霸秘籍】八(下) 第18章 平行四边形-人教版数学-尖子生创优课堂笔记(pdf版)
文档属性
| 名称 | 【学霸秘籍】八(下) 第18章 平行四边形-人教版数学-尖子生创优课堂笔记(pdf版) |  | |
| 格式 | |||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:15 | ||
图片预览

文档简介
第十八章平行四边形
第十八章
平行四边形
18.1平行四边形
1平行四边形的概念
定义
表示方法及解读
图示
注意
平行四边形用符号
平行四边形
伸缩门
两组对边分
“口”表示;平行四边形
D
C
的表示一定
别平行的四
ABCD记作“口ABCD”,
按顺时针或
边形叫做平
网
读作“平行四边形
A
B
逆时针依次
行四边形
庭院的竹篱笆
ABCD”
注明各顶,点
2平行四边形的性质
性质
符号语言
图示
①+★=180°.
平行四边形的
.·四边形ABCD是平行四边形,
边
两组对边分别
.AD=BC,AD//BC,AB=CD,
平行且相等
AB∥CD
S
.四边形ABCD是平行四边形,
S
平行四边形的
D
∴.(1)∠BAD=∠BCD,
两组对角分别
角
S,=S2
∠ABC=∠ADC,
相等,邻角互
B
②平行四边形的两条对
(2)∠ABC+∠BAD=180°,
补
角线将平行四边形分成
∠ADC+∠BAD=180°①
对
的四个三角形中,相对的
平行四边形的
,四边形ABCD是平行四边形,
两个三角形全等,且四个
角
对角线互相平
形
分2
0A=OC-AC.OB-0D=B/
三角形的面积相等
平行四边形具有一般四边形的一切性质
典例(温州中考)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边
规律方法
上,以CB,CD为边作口BCDE,则∠E的度数为(
)
E B
先根据等腰三角形的性
A.40°
B.50°
C.60°
D.70°
质和三角形的内角和定
解析:.∠A=40°,AB=AC,∴.∠ABC=LC=70°
理求出∠C的度数,再根
D C
:四边形BCDE是平行四边形,
据平行四边形的性质解
∠E=∠C=70°.故选D.
答即可
答案:D
85
八年级下
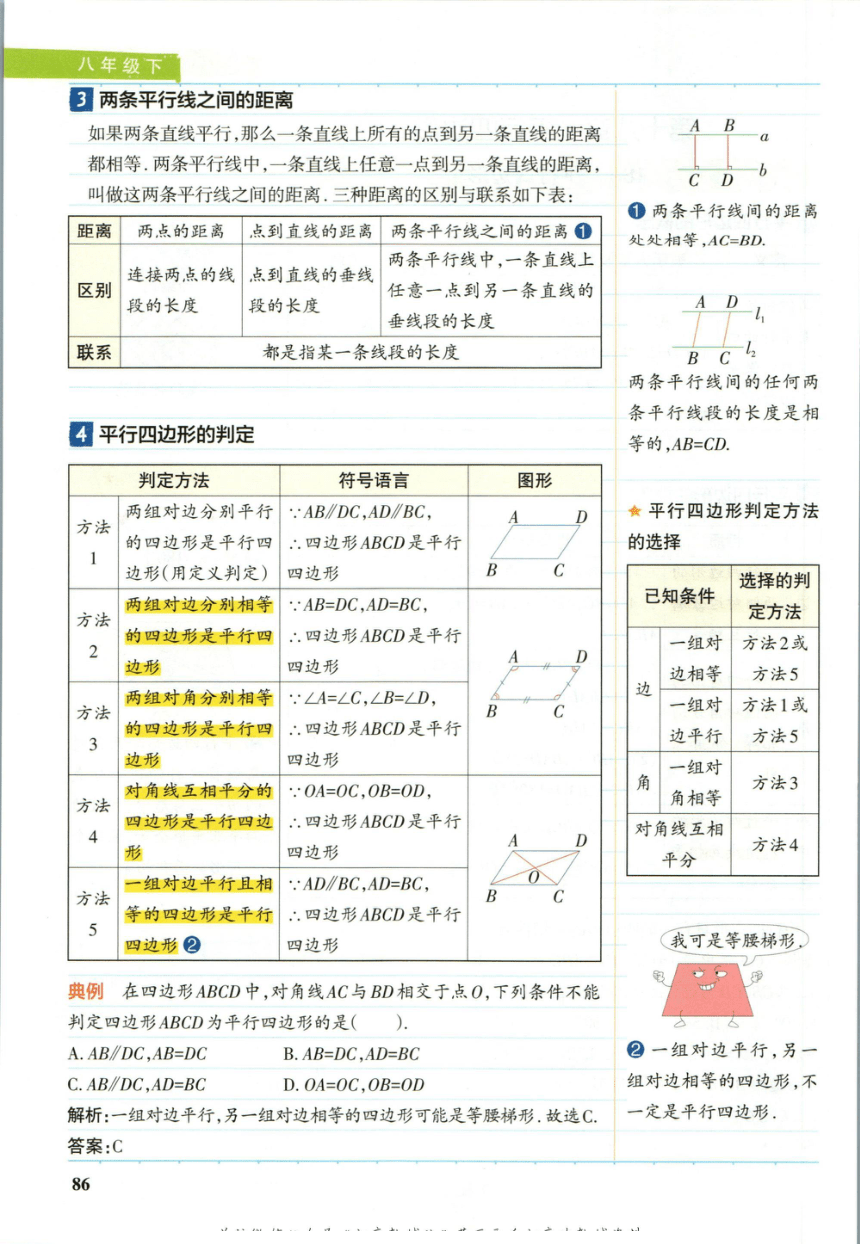
3两条平行线之间的距离
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离
A
B
都相等.两条平行线中,一条直线上任意一点到另一条直线的距离,
—b
叫做这两条平行线之间的距离.三种距离的区别与联系如下表:
①两条平行线间的距离
距离
两,点的距离
点到直线的距离
两条平行线之间的距离①
处处相等,AC=BD
两条平行线中,一条直线上
连接两点的线
点到直线的垂线
区别
任意一点到另一条直线的
段的长度
段的长度
A
垂线段的长度
联系
都是指某一条线段的长度
B C L
两条平行线间的任何两
条平行线段的长度是相
4平行四边形的判定
等的,AB=CD.
判定方法
符号语言
图形
两组对边分别平行
AB//DC,AD//BC,
D
★平行四边形判定方法
方法
的四边形是平行四
.四边形ABCD是平行
的选择
1
边形(用定义判定)
四边形
B
选择的判
两组对边分别相等
.AB=DC,AD=BC,
已知条件
方法
定方法
的四边形是平行四
.四边形ABCD是平行
2
一组对
方法2或
D
边形
四边形
边相等
方法5
两组对角分别相等
.'∠A=∠C,∠B=LD,
边
方法
一组对
方法1或
的四边形是平行四
.四边形ABCD是平行
边平行
方法5
边形
四边形
一组对
对角线互相平分的
.OA=OC,OB=OD,
角
方法3
方法
角相等
四边形是平行四边
.四边形ABCD是平行
对角线互相
形
四边形
方法4
平分
一组对边平行且相
.AD∥BC,AD=BC,
方法
B
等的四边形是平行
.四边形ABCD是平行
5
四边形②
四边形
我可是等腰梯形
典例在四边形ABCD中,对角线AC与BD相交于点O,下列条件不能
判定四边形ABCD为平行四边形的是().
A.AB∥DC,AB=DC
B.AB=DC,AD=BC
②一组对边平行,另一
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
组对边相等的四边形,不
解析:一组对边平行,另一组对边相等的四边形可能是等腰梯形.故选C
一定是平行四边形】
答案:C
86
第十八章
平行四边形
18.1平行四边形
1平行四边形的概念
定义
表示方法及解读
图示
注意
平行四边形用符号
平行四边形
伸缩门
两组对边分
“口”表示;平行四边形
D
C
的表示一定
别平行的四
ABCD记作“口ABCD”,
按顺时针或
边形叫做平
网
读作“平行四边形
A
B
逆时针依次
行四边形
庭院的竹篱笆
ABCD”
注明各顶,点
2平行四边形的性质
性质
符号语言
图示
①+★=180°.
平行四边形的
.·四边形ABCD是平行四边形,
边
两组对边分别
.AD=BC,AD//BC,AB=CD,
平行且相等
AB∥CD
S
.四边形ABCD是平行四边形,
S
平行四边形的
D
∴.(1)∠BAD=∠BCD,
两组对角分别
角
S,=S2
∠ABC=∠ADC,
相等,邻角互
B
②平行四边形的两条对
(2)∠ABC+∠BAD=180°,
补
角线将平行四边形分成
∠ADC+∠BAD=180°①
对
的四个三角形中,相对的
平行四边形的
,四边形ABCD是平行四边形,
两个三角形全等,且四个
角
对角线互相平
形
分2
0A=OC-AC.OB-0D=B/
三角形的面积相等
平行四边形具有一般四边形的一切性质
典例(温州中考)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边
规律方法
上,以CB,CD为边作口BCDE,则∠E的度数为(
)
E B
先根据等腰三角形的性
A.40°
B.50°
C.60°
D.70°
质和三角形的内角和定
解析:.∠A=40°,AB=AC,∴.∠ABC=LC=70°
理求出∠C的度数,再根
D C
:四边形BCDE是平行四边形,
据平行四边形的性质解
∠E=∠C=70°.故选D.
答即可
答案:D
85
八年级下
3两条平行线之间的距离
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离
A
B
都相等.两条平行线中,一条直线上任意一点到另一条直线的距离,
—b
叫做这两条平行线之间的距离.三种距离的区别与联系如下表:
①两条平行线间的距离
距离
两,点的距离
点到直线的距离
两条平行线之间的距离①
处处相等,AC=BD
两条平行线中,一条直线上
连接两点的线
点到直线的垂线
区别
任意一点到另一条直线的
段的长度
段的长度
A
垂线段的长度
联系
都是指某一条线段的长度
B C L
两条平行线间的任何两
条平行线段的长度是相
4平行四边形的判定
等的,AB=CD.
判定方法
符号语言
图形
两组对边分别平行
AB//DC,AD//BC,
D
★平行四边形判定方法
方法
的四边形是平行四
.四边形ABCD是平行
的选择
1
边形(用定义判定)
四边形
B
选择的判
两组对边分别相等
.AB=DC,AD=BC,
已知条件
方法
定方法
的四边形是平行四
.四边形ABCD是平行
2
一组对
方法2或
D
边形
四边形
边相等
方法5
两组对角分别相等
.'∠A=∠C,∠B=LD,
边
方法
一组对
方法1或
的四边形是平行四
.四边形ABCD是平行
边平行
方法5
边形
四边形
一组对
对角线互相平分的
.OA=OC,OB=OD,
角
方法3
方法
角相等
四边形是平行四边
.四边形ABCD是平行
对角线互相
形
四边形
方法4
平分
一组对边平行且相
.AD∥BC,AD=BC,
方法
B
等的四边形是平行
.四边形ABCD是平行
5
四边形②
四边形
我可是等腰梯形
典例在四边形ABCD中,对角线AC与BD相交于点O,下列条件不能
判定四边形ABCD为平行四边形的是().
A.AB∥DC,AB=DC
B.AB=DC,AD=BC
②一组对边平行,另一
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
组对边相等的四边形,不
解析:一组对边平行,另一组对边相等的四边形可能是等腰梯形.故选C
一定是平行四边形】
答案:C
86
同课章节目录
