【学霸秘籍】九(上) 第22章 二次函数-人教版数学-尖子生创优课堂笔记(pdf版)
文档属性
| 名称 | 【学霸秘籍】九(上) 第22章 二次函数-人教版数学-尖子生创优课堂笔记(pdf版) |  | |
| 格式 | |||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:15 | ||
图片预览


文档简介
第二十二章'二次函数
第二十二章二次函数
一次项系数
22.1二次函数的图象和性质
★y=ax2+bx+c(a≠0)
1二次函数
二次项系数
常数项
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函
判断一个函数是否为二
数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次
次函数,首先将其化简为
项系数和常数项
一般形式,然后与二次函
2二次函数y=ax和y=a(x-h)2+k的图象与性质
数的一般形式对比,只有
形式完全一样的才是二
函数
y=ax2(a≠0)
y=a(x-h))2+k(a≠0)
次函数
类别
y↑x=h
图象0
0元on
a>0
a<0
a>0
a<0
a>0,开口向上,并向上无限
a>0,开口向上,并向上无限
开口方
延伸;a<0,开口向下,并向
延伸;a<0,开口向下,并向
①喷泵喷出的水柱类似
向及其
下无限延伸;
下无限延伸;
于抛物线形状」
大小
a越大,开口越小;
a越大,开口越小;
a越小,开口越大
a越小,开口越大
不管天
我们形
对称轴
直线x=0(y轴)
直线x=h
涯海角,
影不离
顶点坐标
(0,0)
(h,k)
a>0,x<0(x>0)时,即在对称
a>0,xh)时,即在对称
a>0
最小值
轴的左侧(右侧),y随x的
轴的左侧(右侧),y随x的增
增大而减小(增大)
大而减小(增大)
哪怕海
我们同
增减性
a<0,x<0(>0)时,即在对称
a<0,xh)时,即在对称
枯石烂
生共死
轴的左侧(右侧),y随x的
轴的左侧(右侧),y随x的增
oo
增大而增大(减小)
大而增大(减小)
a<0
/5的
最大值
a>0时,二次函数有最小值,
a>0时,二次函数有最小
②(1)当a>0时,二次函
即当x=0时,y小=0,此时
值,即当x=h时,y小值=k,此
数有最小值;
最低,点为顶点(0,0);
时最低,点为顶,点(h,k);
最值②
(2)当a<0时,二次函数
a<0时,二次函数有最大值,
a<0时,二次函数有最大
有最大值。
即当x=0时,y最大值=0,此时
值,即当x=h时,y大值=k,此
最高点为顶,点(0,0)
时最高点为顶点(h,k)
107
九年级上
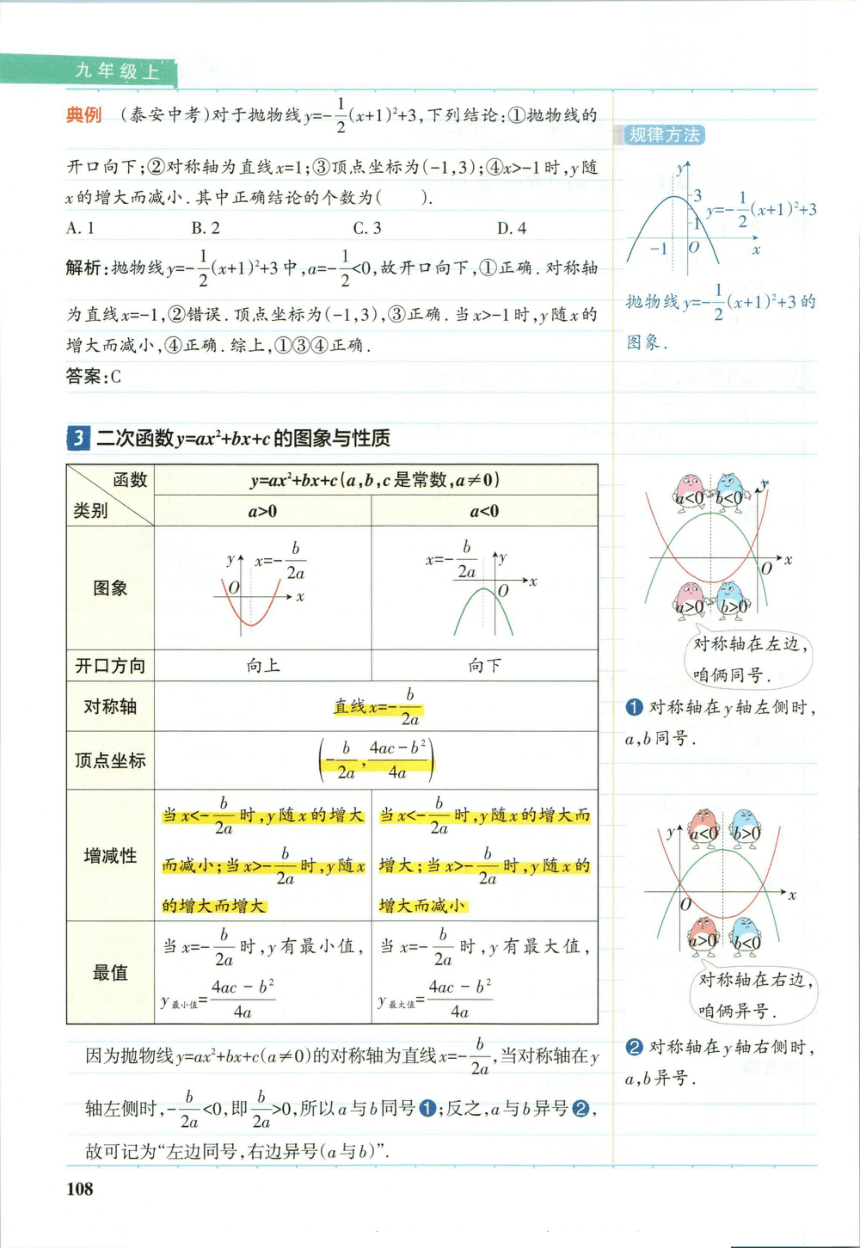
典例(秦安中考)对于抛物线)=x+1)3,下列结论:①抛物线的
规律方法
开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>-1时,y随
x的增大而减小.其中正确结论的个数为(
-(x+1)2+3
A.1
B.2
C.3
D.4
解析:抛物线=一
2x+1P+3中,a
1
20,故开口向下,①正确.对称轴
为直线x=-1,②错误.顶点坐标为(-1,3),③正确.当>-1时,y随x的
抛物线)2x+1)P+3的
增大而减小,④正确.综上,①③④正确
图象
答案:C
3二次函数y=ax2+bx+c的图象与性质
函数
y=ax2+bx+c(a,b,c是常数,a≠0)
类别
竹
a>0
a<0
b
b
y↑x=
x=-
:↑y
2a
2a
图象
x
>0b>亦
对称轴在左边,
开口方向
向上
向下
咱俩同号.
对称轴
直线2
①对称轴在y轴左侧时,
b
4ac-b2
a,b同号.
顶点坐标
2a’4a
b
当x<-
0
时,y随x的增大
当x<-
2a
时,y随x的增大而
a<0b>0
增减性
b
而减小;当x>-。时,y随x
2a
增大;当x
时,y随x的
2a
的增大而增大
增大而减小小
当x=-
0时,y有最小值
当x=-
6时,y有最大值
>06<0
A
最值
4ac-b2
4ac b2
对称轴在右边,
Y最小值=
4a
Y最大位三
4a
咱俩异号
当对称轴在,
b
因为抛物线y=ax+bx+c(a≠0)的对称轴为直线x=-
②对称轴在y轴右侧时,
a,b异号.
轴左侧时,六0,即名0,所以a与6同号0:反之.a与6异号@,
故可记为“左边同号,右边异号(a与b)”
108
第二十二章二次函数
一次项系数
22.1二次函数的图象和性质
★y=ax2+bx+c(a≠0)
1二次函数
二次项系数
常数项
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函
判断一个函数是否为二
数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次
次函数,首先将其化简为
项系数和常数项
一般形式,然后与二次函
2二次函数y=ax和y=a(x-h)2+k的图象与性质
数的一般形式对比,只有
形式完全一样的才是二
函数
y=ax2(a≠0)
y=a(x-h))2+k(a≠0)
次函数
类别
y↑x=h
图象0
0元on
a>0
a<0
a>0
a<0
a>0,开口向上,并向上无限
a>0,开口向上,并向上无限
开口方
延伸;a<0,开口向下,并向
延伸;a<0,开口向下,并向
①喷泵喷出的水柱类似
向及其
下无限延伸;
下无限延伸;
于抛物线形状」
大小
a越大,开口越小;
a越大,开口越小;
a越小,开口越大
a越小,开口越大
不管天
我们形
对称轴
直线x=0(y轴)
直线x=h
涯海角,
影不离
顶点坐标
(0,0)
(h,k)
a>0,x<0(x>0)时,即在对称
a>0,x
a>0
最小值
轴的左侧(右侧),y随x的
轴的左侧(右侧),y随x的增
增大而减小(增大)
大而减小(增大)
哪怕海
我们同
增减性
a<0,x<0(>0)时,即在对称
a<0,x
枯石烂
生共死
轴的左侧(右侧),y随x的
轴的左侧(右侧),y随x的增
oo
增大而增大(减小)
大而增大(减小)
a<0
/5的
最大值
a>0时,二次函数有最小值,
a>0时,二次函数有最小
②(1)当a>0时,二次函
即当x=0时,y小=0,此时
值,即当x=h时,y小值=k,此
数有最小值;
最低,点为顶点(0,0);
时最低,点为顶,点(h,k);
最值②
(2)当a<0时,二次函数
a<0时,二次函数有最大值,
a<0时,二次函数有最大
有最大值。
即当x=0时,y最大值=0,此时
值,即当x=h时,y大值=k,此
最高点为顶,点(0,0)
时最高点为顶点(h,k)
107
九年级上
典例(秦安中考)对于抛物线)=x+1)3,下列结论:①抛物线的
规律方法
开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>-1时,y随
x的增大而减小.其中正确结论的个数为(
-(x+1)2+3
A.1
B.2
C.3
D.4
解析:抛物线=一
2x+1P+3中,a
1
20,故开口向下,①正确.对称轴
为直线x=-1,②错误.顶点坐标为(-1,3),③正确.当>-1时,y随x的
抛物线)2x+1)P+3的
增大而减小,④正确.综上,①③④正确
图象
答案:C
3二次函数y=ax2+bx+c的图象与性质
函数
y=ax2+bx+c(a,b,c是常数,a≠0)
类别
竹
a>0
a<0
b
b
y↑x=
x=-
:↑y
2a
2a
图象
x
>0b>亦
对称轴在左边,
开口方向
向上
向下
咱俩同号.
对称轴
直线2
①对称轴在y轴左侧时,
b
4ac-b2
a,b同号.
顶点坐标
2a’4a
b
当x<-
0
时,y随x的增大
当x<-
2a
时,y随x的增大而
a<0b>0
增减性
b
而减小;当x>-。时,y随x
2a
增大;当x
时,y随x的
2a
的增大而增大
增大而减小小
当x=-
0时,y有最小值
当x=-
6时,y有最大值
>06<0
A
最值
4ac-b2
4ac b2
对称轴在右边,
Y最小值=
4a
Y最大位三
4a
咱俩异号
当对称轴在,
b
因为抛物线y=ax+bx+c(a≠0)的对称轴为直线x=-
②对称轴在y轴右侧时,
a,b异号.
轴左侧时,六0,即名0,所以a与6同号0:反之.a与6异号@,
故可记为“左边同号,右边异号(a与b)”
108
同课章节目录
