青岛版(2012)数学八年级上册第五章几何证明初步章节拔高练习(含答案)
文档属性
| 名称 | 青岛版(2012)数学八年级上册第五章几何证明初步章节拔高练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 537.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览



文档简介
青岛版(2012)数学八年级上册第五章几何证明初步章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个三角形的三个内角度数之比为,则这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
2.如图,在中,,,是的平分线,则( )
A. B. C. D.
3.下列说法错误的是:( )
A.直角三角形的两个锐角互为余角
B.(n+1)边形的内角和比n边形的内角和大 180°
C.连接轴对称图形的对应点的线段必被对称轴垂直平分
D.△ABC≌△DEF,则△ABC与△DEF一定关于某条直线对称
4.在中,,,点在边上(不与点,重合),点、点分别是,边上的动点,当的周长最小时,的度数是( )
A.70° B.90° C.100° D.120°
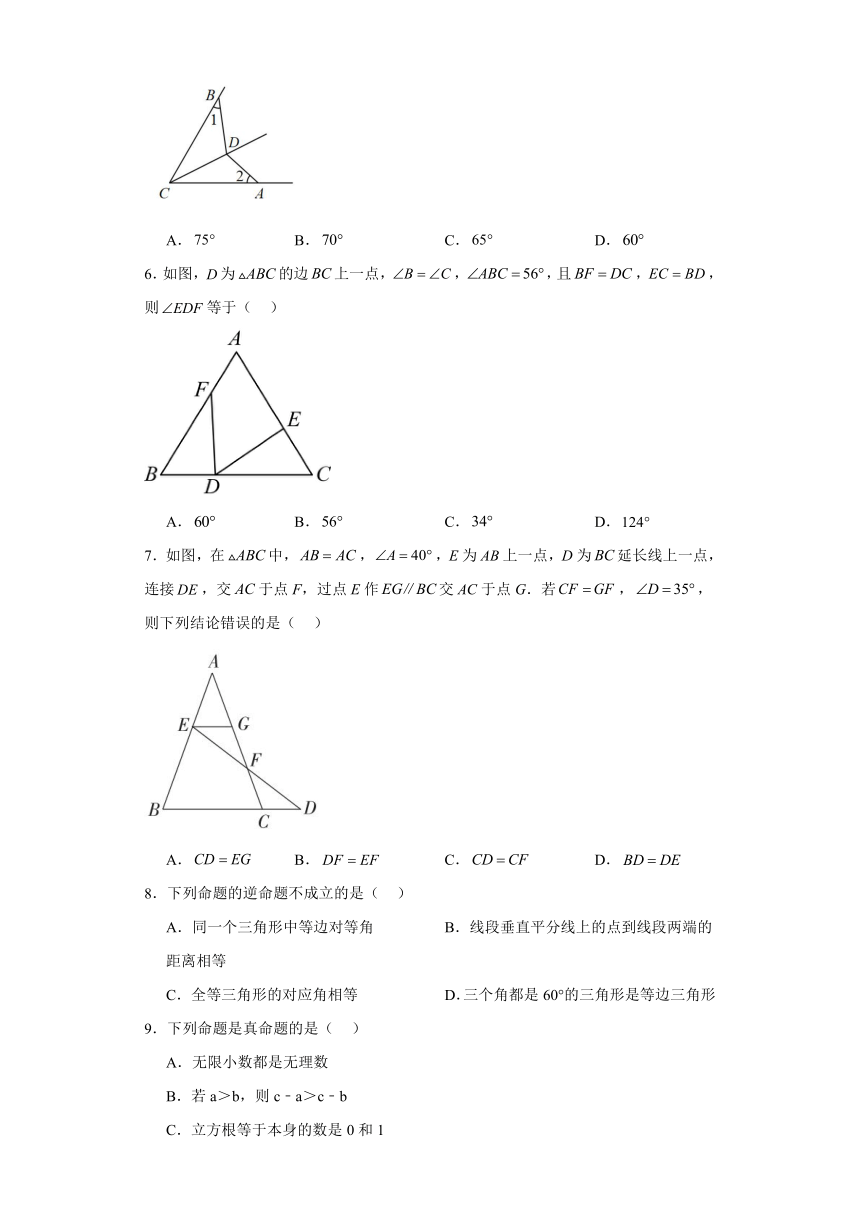
5.如图所示,点D是内一点,若,,,则的大小为( )
A. B. C. D.
6.如图,为的边上一点,,,且,,则等于( )
A. B. C. D.
7.如图,在中,,,E为上一点,D为延长线上一点,连接,交于点F,过点E作交AC于点G.若,,则下列结论错误的是( )
A. B. C. D.
8.下列命题的逆命题不成立的是( )
A.同一个三角形中等边对等角 B.线段垂直平分线上的点到线段两端的距离相等
C.全等三角形的对应角相等 D.三个角都是60°的三角形是等边三角形
9.下列命题是真命题的是( )
A.无限小数都是无理数
B.若a>b,则c﹣a>c﹣b
C.立方根等于本身的数是0和1
D.平面内如果两条直线都和第三条直线垂直,那么这两条直线互相平行
10.下列图形中,由,能得到的是( )
A. B.
C. D.
二、填空题
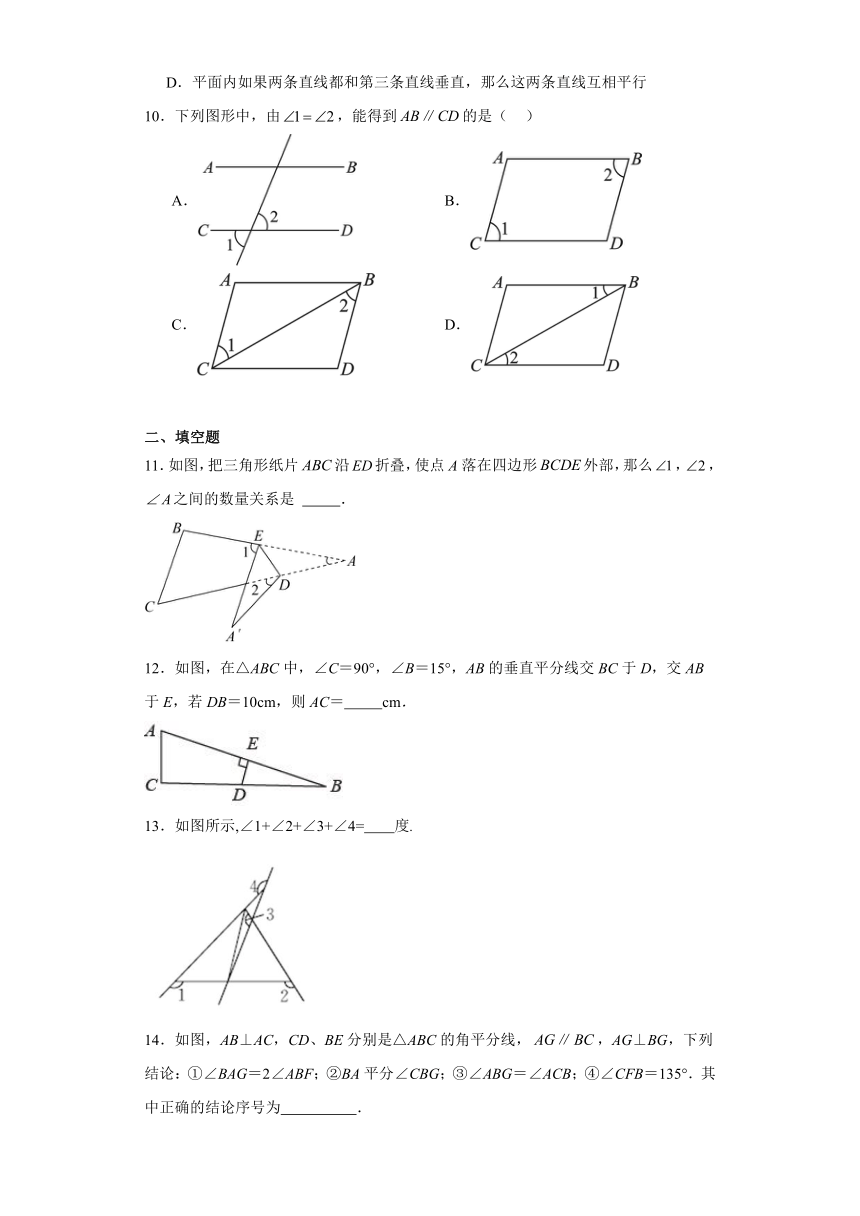
11.如图,把三角形纸片沿折叠,使点A落在四边形外部,那么,,之间的数量关系是 .
12.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则AC= cm.
13.如图所示,∠1+∠2+∠3+∠4= 度.
14.如图,AB⊥AC,CD、BE分别是△ABC的角平分线,,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论序号为 .
15.如图,AD是△ABC的外角平分线,∠B=,∠DAE=65°,∠ACD等于 .
16.如图,中,,为的平分线,,则的度数是 .
17.如图,AD平分∠BAC,EC∥AD,若∠B=30°,∠ACB=40°,则∠E= °.
18.如图,在中,,将绕点C顺时针旋转得到,P为线段上的动点.以P为圆心、为半径作,当与的边相切时,的半径长为 .
19.如图,直线AB∥CD,∠B=60°,∠C=40°,则∠E等于 .
20.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=25°,则∠B的度数为 .
三、解答题
21.在中,点在边上,,
(1)如图1,求证:平分.
(2)如图2,过点作直线,请直接写出、和的数量关系________.
(3)如图3,在(2)的条件下,点在线段上,交于点,,且,点在的延长线上,与延长线交于点,满足,若,连接,,,求线段的长.
22.某中学八年级学生到野外开展数学综合实践活动,在营地看到一个不规则的建筑物,为测量该建筑物两端A,B间的距离,但同学们给出了以下建议:
(1)甲同学的方案如下:先在平地上取一个可直接到达A,B的点O,连接,,并分别延长至点C,延长至点D,使,,最后测出的长即为A,B间的距离,请你说说该方案可行的理由;
(2)由于在处有一堵墙阻挡了路线,使得无法按照甲同学的方案直接测量出A,B间的距离,但同学们测得,,,,,请求出该建筑物两端A,B之间的距离.
23.如图,点分别是等边边上的动点(端点除外),点从顶点、点从顶点同时出发,且它们的运动速度相同,连接交于点.
(1)与全等吗?请说明理由;
(2)当点分别在边上运动时,变化吗?若变化,请说明理由;若不变, 求出它的度数.
24.填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:
解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_____=90°(垂直定义)
∴DG∥AC,(____________________)
∴∠2=∠_________.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠________(等量代换)
∴EF∥______(同位角相等,两直线平行)
∴∠AEF=∠ADC,(________________)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
25.如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,则∠DAE= .
(2)若∠B=60°,∠C=20°,则∠DAE= .
(3)由(1)(2)猜想∠DAE与∠B,∠C之间的关系为 ,请说明理由.
26.问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板的两条直角边,点A与点P在直线的同侧,若点P在内部,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则 度, 度, 度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在外,其它条件都不变(2)中的结论是否仍然成立?若成立,请说明理由,请直接写出与满足的数量关系式.
27.如图,等边三角形ABC中,BD⊥AC,垂足为点D,E是BC延长线上一点,且CE=BC.请从图中找出除△ABC外所有的等腰三角形,并说明理由.
参考答案:
1.C
2.C
3.D
4.B
5.B
6.B
7.D
8.C
9.D
10.D
11.
12.5
13.540
14.①③④
15.80
16./20度
17.55°
18.或
19.80°
20.65°
21.(1)略
(2)
(3)
22.(1)甲同学的方案可行; (2)该建筑物两端A,B之间的距离为.
23.(1)全等,
(2)不变,
24.∠ACB;同位角相等,两直线平行;∠ACD;∠ACD;CD;两直线平行,同位角相等.
25.(1)10°;(2)20°;(3)∠DAE=(∠B﹣∠C),
26.(1)125,90,35
(2),
(3)(2)中的结论不成立,结论:或,
27.略
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个三角形的三个内角度数之比为,则这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
2.如图,在中,,,是的平分线,则( )
A. B. C. D.
3.下列说法错误的是:( )
A.直角三角形的两个锐角互为余角
B.(n+1)边形的内角和比n边形的内角和大 180°
C.连接轴对称图形的对应点的线段必被对称轴垂直平分
D.△ABC≌△DEF,则△ABC与△DEF一定关于某条直线对称
4.在中,,,点在边上(不与点,重合),点、点分别是,边上的动点,当的周长最小时,的度数是( )
A.70° B.90° C.100° D.120°
5.如图所示,点D是内一点,若,,,则的大小为( )
A. B. C. D.
6.如图,为的边上一点,,,且,,则等于( )
A. B. C. D.
7.如图,在中,,,E为上一点,D为延长线上一点,连接,交于点F,过点E作交AC于点G.若,,则下列结论错误的是( )
A. B. C. D.
8.下列命题的逆命题不成立的是( )
A.同一个三角形中等边对等角 B.线段垂直平分线上的点到线段两端的距离相等
C.全等三角形的对应角相等 D.三个角都是60°的三角形是等边三角形
9.下列命题是真命题的是( )
A.无限小数都是无理数
B.若a>b,则c﹣a>c﹣b
C.立方根等于本身的数是0和1
D.平面内如果两条直线都和第三条直线垂直,那么这两条直线互相平行
10.下列图形中,由,能得到的是( )
A. B.
C. D.
二、填空题
11.如图,把三角形纸片沿折叠,使点A落在四边形外部,那么,,之间的数量关系是 .
12.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则AC= cm.
13.如图所示,∠1+∠2+∠3+∠4= 度.
14.如图,AB⊥AC,CD、BE分别是△ABC的角平分线,,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论序号为 .
15.如图,AD是△ABC的外角平分线,∠B=,∠DAE=65°,∠ACD等于 .
16.如图,中,,为的平分线,,则的度数是 .
17.如图,AD平分∠BAC,EC∥AD,若∠B=30°,∠ACB=40°,则∠E= °.
18.如图,在中,,将绕点C顺时针旋转得到,P为线段上的动点.以P为圆心、为半径作,当与的边相切时,的半径长为 .
19.如图,直线AB∥CD,∠B=60°,∠C=40°,则∠E等于 .
20.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=25°,则∠B的度数为 .
三、解答题
21.在中,点在边上,,
(1)如图1,求证:平分.
(2)如图2,过点作直线,请直接写出、和的数量关系________.
(3)如图3,在(2)的条件下,点在线段上,交于点,,且,点在的延长线上,与延长线交于点,满足,若,连接,,,求线段的长.
22.某中学八年级学生到野外开展数学综合实践活动,在营地看到一个不规则的建筑物,为测量该建筑物两端A,B间的距离,但同学们给出了以下建议:
(1)甲同学的方案如下:先在平地上取一个可直接到达A,B的点O,连接,,并分别延长至点C,延长至点D,使,,最后测出的长即为A,B间的距离,请你说说该方案可行的理由;
(2)由于在处有一堵墙阻挡了路线,使得无法按照甲同学的方案直接测量出A,B间的距离,但同学们测得,,,,,请求出该建筑物两端A,B之间的距离.
23.如图,点分别是等边边上的动点(端点除外),点从顶点、点从顶点同时出发,且它们的运动速度相同,连接交于点.
(1)与全等吗?请说明理由;
(2)当点分别在边上运动时,变化吗?若变化,请说明理由;若不变, 求出它的度数.
24.填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:
解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_____=90°(垂直定义)
∴DG∥AC,(____________________)
∴∠2=∠_________.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠________(等量代换)
∴EF∥______(同位角相等,两直线平行)
∴∠AEF=∠ADC,(________________)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
25.如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,则∠DAE= .
(2)若∠B=60°,∠C=20°,则∠DAE= .
(3)由(1)(2)猜想∠DAE与∠B,∠C之间的关系为 ,请说明理由.
26.问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板的两条直角边,点A与点P在直线的同侧,若点P在内部,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则 度, 度, 度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在外,其它条件都不变(2)中的结论是否仍然成立?若成立,请说明理由,请直接写出与满足的数量关系式.
27.如图,等边三角形ABC中,BD⊥AC,垂足为点D,E是BC延长线上一点,且CE=BC.请从图中找出除△ABC外所有的等腰三角形,并说明理由.
参考答案:
1.C
2.C
3.D
4.B
5.B
6.B
7.D
8.C
9.D
10.D
11.
12.5
13.540
14.①③④
15.80
16./20度
17.55°
18.或
19.80°
20.65°
21.(1)略
(2)
(3)
22.(1)甲同学的方案可行; (2)该建筑物两端A,B之间的距离为.
23.(1)全等,
(2)不变,
24.∠ACB;同位角相等,两直线平行;∠ACD;∠ACD;CD;两直线平行,同位角相等.
25.(1)10°;(2)20°;(3)∠DAE=(∠B﹣∠C),
26.(1)125,90,35
(2),
(3)(2)中的结论不成立,结论:或,
27.略
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
