【学霸秘籍】八(下) 第1章 三角形的证明-北师大版数学-尖子生创优课堂笔记(pdf版)
文档属性
| 名称 | 【学霸秘籍】八(下) 第1章 三角形的证明-北师大版数学-尖子生创优课堂笔记(pdf版) |  | |
| 格式 | |||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:15 | ||
图片预览

文档简介
八年级下
第一章三角形的证明
1等腰三角形
1全等三角形的判定方法及性质
1.全等三角形的判定
。基本事实:两边及其夹角分别相等的两个三角形全等.(SAS)
o基本事实:两角及其夹边分别相等的两个三角形全等.(ASA)
B
。基本事实:三边分别相等的两个三角形全等.(SSS)》
D
。定理:两角分别相等且其中一组等角的对边相等的两个三角形全
★若△ABD≌△ACD,则
等.(AAS)
AB=AC,AD=AD,BD=
2.全等三角形的性质:全等三角形的对应边相等、对应角相等
CD,∠B=∠C,∠BAD=
∠CAD,∠ADB=∠ADC
2等腰三角形的性质
1.定理:等腰三角形的两底角相等.这一定理可以简述为:等边对等角.
2.推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互
相重合(简写成“三线合一”)
★等腰三角形是轴对称
典例(苏州中考)如图,在△ABC中,点D在BC上,
图形,底边上的中线
AB=AD=DC,∠B=80°,则∠C的度数为().
(顶角的平分线、底边
A.30°
B.40°
C.45
D.60°
上的高线)所在直线就
解析:AB=AD,∠ADB=∠B=80°
B D
是它的对称轴
.AD=DC,∠C=∠CAD
∴.∠ADB=∠C+∠CAD=2∠C=80°,.∴.∠C=40°
我两边长相等,我才
答案:B
是等腰三角形呢!
3Λ0
3等腰三角形的判定定理
定理:有两个角相等的三角形是等腰三角形
这一定理可以简述为:等角对等边
我两个角相等,
典例如图,在△ABC中,AB=AC,过BC上一,点D作BC的垂线,交BA
我是等腰三角形,
的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论
解:△APQ为等腰三角形
★判定等腰三角形的方法
有两个:一是等腰三角
证明:'AB=AC,∴∠B=∠C
又.PDLBC,.∠B+∠P=∠C+∠CQD=90°,
形的定义,即有两条边
相等的三角形是等腰
.∠P=∠CQD=LAQP,∴.AP=AQ,
三角形;二是判定定理」
∴,△APQ为等腰三角形
96
第一章三角形的证明
4反证法
你怎么不
1.反证法的定义
摘李子呢?
在证明时,先假设命题的结论不成立,然后推导出与定义、基本事
实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定
李子是
成立.这种证明方法称为反证法
苦的
2.使用反证法证明问题的一般步骤
。反设:假定所要证的结论不成立,而设结论的反面成立;
。归谬:将“反设”作为条件,由此出发经过正确的推导,导出与定
假设李子是甜的
义、基本事实、定理及已知条件相矛盾或自相矛盾的结论;
那么李子会被过路人摘去
。结论:因为推理正确,产生矛盾的原因在于“反设”的谬误,既然结
解渴,树上的李子会很少
↓
论的反面不成立,那么结论一定成立.
事实上,树上的李子很
多,这与事实相矛盾
5等边三角形的判定定理及性质
1.判定定理
假设不成立,李子是苦的.
Q三个角都相等的三角形是等边三角形
。有一个角等于60°的等腰三角形是等边三角形
2.性质:等边三角形的三个内角都相等,并且每个角都等于60°
3030
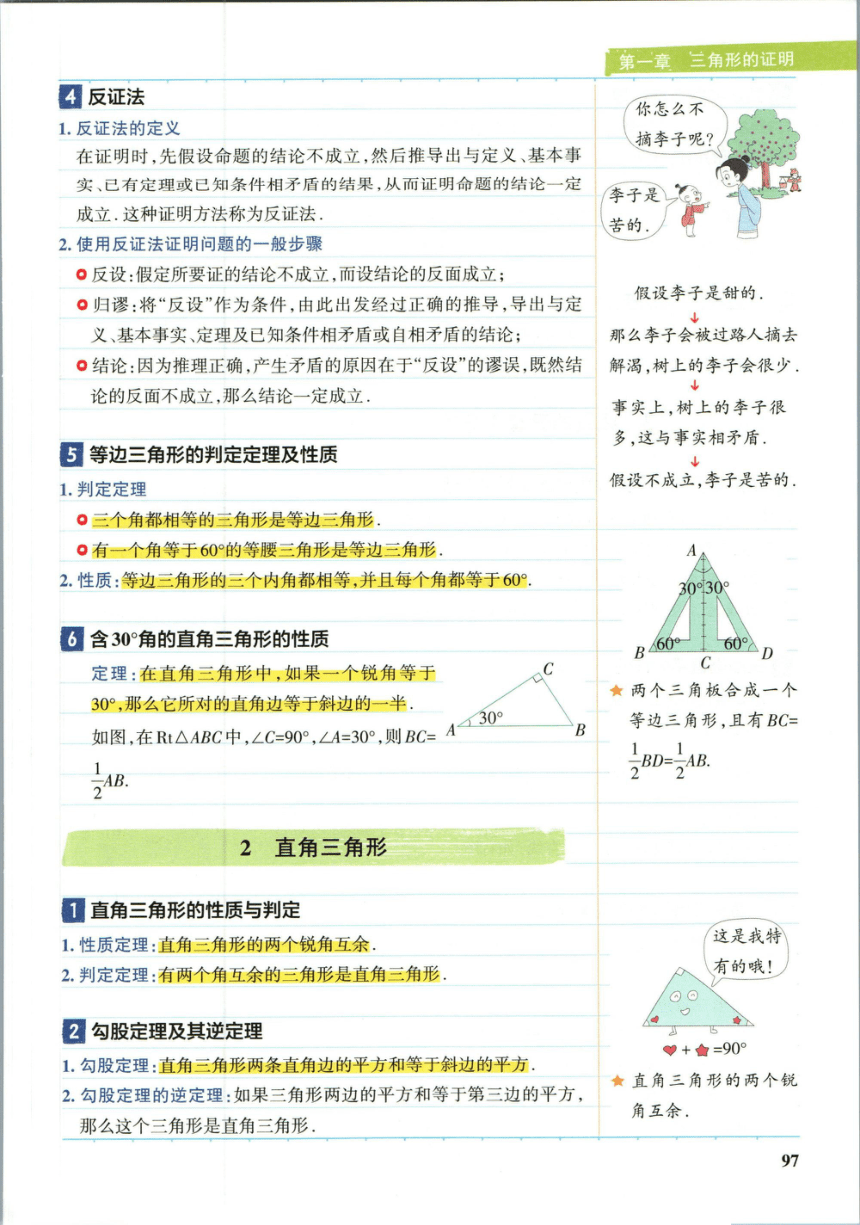
6含30°角的直角三角形的性质
B460
60°
C
定理:在直角三角形中,如果一个锐角等于
C
食两个三角板合成一个
30°,那么它所对的直角边等于斜边的一半
如图,在R△1MBG中,∠G=90,∠A=30,则BCA30
等边三角形,且有BC=
0)1a
1
2
2直角三角形
1直角三角形的性质与判定
1.性质定理:直角三角形的两个锐角互余
这是我特
2.判定定理:有两个角互余的三角形是直角三角形
有的哦!
⊙@
2勾股定理及其逆定理
9+☆=90
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方
食直角三角形的两个锐
2.勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,
角互余
那么这个三角形是直角三角形
97
第一章三角形的证明
1等腰三角形
1全等三角形的判定方法及性质
1.全等三角形的判定
。基本事实:两边及其夹角分别相等的两个三角形全等.(SAS)
o基本事实:两角及其夹边分别相等的两个三角形全等.(ASA)
B
。基本事实:三边分别相等的两个三角形全等.(SSS)》
D
。定理:两角分别相等且其中一组等角的对边相等的两个三角形全
★若△ABD≌△ACD,则
等.(AAS)
AB=AC,AD=AD,BD=
2.全等三角形的性质:全等三角形的对应边相等、对应角相等
CD,∠B=∠C,∠BAD=
∠CAD,∠ADB=∠ADC
2等腰三角形的性质
1.定理:等腰三角形的两底角相等.这一定理可以简述为:等边对等角.
2.推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互
相重合(简写成“三线合一”)
★等腰三角形是轴对称
典例(苏州中考)如图,在△ABC中,点D在BC上,
图形,底边上的中线
AB=AD=DC,∠B=80°,则∠C的度数为().
(顶角的平分线、底边
A.30°
B.40°
C.45
D.60°
上的高线)所在直线就
解析:AB=AD,∠ADB=∠B=80°
B D
是它的对称轴
.AD=DC,∠C=∠CAD
∴.∠ADB=∠C+∠CAD=2∠C=80°,.∴.∠C=40°
我两边长相等,我才
答案:B
是等腰三角形呢!
3Λ0
3等腰三角形的判定定理
定理:有两个角相等的三角形是等腰三角形
这一定理可以简述为:等角对等边
我两个角相等,
典例如图,在△ABC中,AB=AC,过BC上一,点D作BC的垂线,交BA
我是等腰三角形,
的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论
解:△APQ为等腰三角形
★判定等腰三角形的方法
有两个:一是等腰三角
证明:'AB=AC,∴∠B=∠C
又.PDLBC,.∠B+∠P=∠C+∠CQD=90°,
形的定义,即有两条边
相等的三角形是等腰
.∠P=∠CQD=LAQP,∴.AP=AQ,
三角形;二是判定定理」
∴,△APQ为等腰三角形
96
第一章三角形的证明
4反证法
你怎么不
1.反证法的定义
摘李子呢?
在证明时,先假设命题的结论不成立,然后推导出与定义、基本事
实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定
李子是
成立.这种证明方法称为反证法
苦的
2.使用反证法证明问题的一般步骤
。反设:假定所要证的结论不成立,而设结论的反面成立;
。归谬:将“反设”作为条件,由此出发经过正确的推导,导出与定
假设李子是甜的
义、基本事实、定理及已知条件相矛盾或自相矛盾的结论;
那么李子会被过路人摘去
。结论:因为推理正确,产生矛盾的原因在于“反设”的谬误,既然结
解渴,树上的李子会很少
↓
论的反面不成立,那么结论一定成立.
事实上,树上的李子很
多,这与事实相矛盾
5等边三角形的判定定理及性质
1.判定定理
假设不成立,李子是苦的.
Q三个角都相等的三角形是等边三角形
。有一个角等于60°的等腰三角形是等边三角形
2.性质:等边三角形的三个内角都相等,并且每个角都等于60°
3030
6含30°角的直角三角形的性质
B460
60°
C
定理:在直角三角形中,如果一个锐角等于
C
食两个三角板合成一个
30°,那么它所对的直角边等于斜边的一半
如图,在R△1MBG中,∠G=90,∠A=30,则BCA30
等边三角形,且有BC=
0)1a
1
2
2直角三角形
1直角三角形的性质与判定
1.性质定理:直角三角形的两个锐角互余
这是我特
2.判定定理:有两个角互余的三角形是直角三角形
有的哦!
⊙@
2勾股定理及其逆定理
9+☆=90
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方
食直角三角形的两个锐
2.勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,
角互余
那么这个三角形是直角三角形
97
同课章节目录
