【学霸秘籍】九(下) 第2章 二次函数-北师大版数学-尖子生创优课堂笔记(pdf版)
文档属性
| 名称 | 【学霸秘籍】九(下) 第2章 二次函数-北师大版数学-尖子生创优课堂笔记(pdf版) |  | |
| 格式 | |||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:15 | ||
图片预览

文档简介
第二章二次函数
第二章
二次函数
1二次函数
二次项一次项
■二次函数的概念
系数a≠0系数
常数项
1.概念:一般地,若两个变量x,y之间的对应关系可以表示成y=ax2+
←
bx+c(a,b,c是常数,a≠0)的形式,则称y是x的二次函数
y=axkxt
2.二次函数值:已知二次函数的表达式,计算它的函数值,只需将自变
★自变量的最高次数是
量x所取的值代入表达式中,计算出结果
2;二次项系数不能为
0,而一次项系数、常
2二次函数的图象与性质
数项可以为0;函数的
表达式是整式
1二次函数y=ar和y=a(x-h)2+k的图象与性质
y=ax2
y=a(x-h)2+k
y个x=h
图象
0xo
a>0a<0
a>0
a<0
个y
a>0,开口向上,并向上无限延伸;
开口方向
a<0,开口向下,并向下无限延伸
1y=-2x2
开口大小
|a越大,开口越小;a越小,开口越大
对称轴
直线x=0(y轴)
直线x=h
★喷泉喷出的水柱类似
顶点坐标
(0,0)
(h,k)
于抛物线形状
x>0时,即在对称轴的右
x>h时,即在对称轴的右侧,y
侧,y的值随x值的增大而
的值随x值的增大而增大
增大(a>0时)或减小(a<0
最高点
(a>0时)或减小(a<0时)
时)
增减性
x<0时,即在对称轴的左
x侧,y的值随x值的增大而
的值随x值的增大而减小
减小(a>0时)或增大(a<0
(a>0时)或增大(a<0时)
时)
★投篮时,篮球的运动轨
a>0时,二次函数有最小a>0时,二次函数有最小值,
迹类似于抛物线形状.
值,即当x=0时,y小值=0;
即当x=h时,y最小值=k;
最值
a<0时,二次函数有最大
a<0时,二次函数有最大值,
值,即当x=0时,y最大值=0
即当x=h时,y最大值=k
143
九年级下
典例(泰安中考)对于抛物线)=子x+1)43,下列结论:①抛物线的
开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3)④x>-1时,y随
x的增大而减小.其中正确结论的个数为(
).
a>0,c<0a<0,c>0
A.1
B.2
C.3
D.4
★抛物线y=ax2+bx+c(a≠
解折:郑物线+13中,a=
20,故开口向下,①正确」
0)与y轴交点在x轴上
方(即交于y轴正半
对称轴为直线x=-1,②错误,
轴)时,c>0;反之,c<0.
顶,点坐标为(-1,3),③正确
故可记为“a看开口,c
当x>-1时,y随x的增大而减小,④正确.综上,①③④正确
看截距”
答案:C
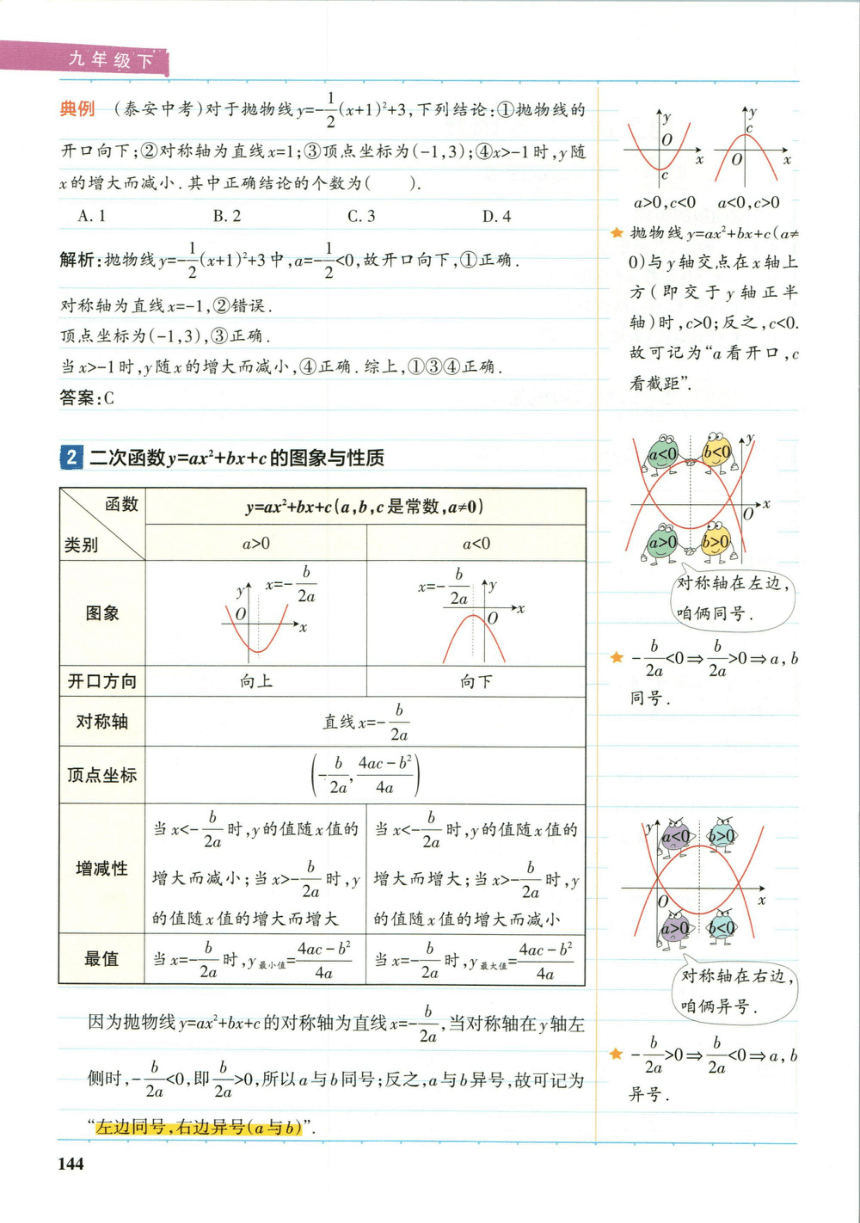
2二次函数y=ax2+b.x+c的图象与性质
函数
y=ax2+bx+c(a,b,c是常数,a≠0)
类别
a>0
a<0
>
b
b
对称轴在左边,
2a
X=一
↑y
2a
图象
0
咱俩同号.
★、
<0→6>09a,b
开口方向
2a
2a
向上
向下
同号.
b
对称轴
直线x=
2a
b 4ac-b2
顶点坐标
2a'
4a
当x<-
时,y的值随x值的
当x<
b
2a
时,y的值随x值的
2a
00
增减性
增大而减小;当>
b
时,y
2a
增大而增大;当x>
时,y
2a
的值随x值的增大而增大
的值随x值的增大而减小
6<0
b
最值
当x=
4ac-b2
b
时,y最小值
当x=
4ac-b2
2a
Aa
时,y最大值
2a
Aa
对称轴在右边,
b
咱俩异号
因为抛物线y=ax2+bx+c的对称轴为直线x=
,当对称轴在y轴左
2a
0,即会0,所以a与6同号:反之与6异号,放可记为
一
b
0户
侧时,一
a
b<0→a,b
异号
“左边同号,右边异号(a与b)”
144
第二章
二次函数
1二次函数
二次项一次项
■二次函数的概念
系数a≠0系数
常数项
1.概念:一般地,若两个变量x,y之间的对应关系可以表示成y=ax2+
←
bx+c(a,b,c是常数,a≠0)的形式,则称y是x的二次函数
y=axkxt
2.二次函数值:已知二次函数的表达式,计算它的函数值,只需将自变
★自变量的最高次数是
量x所取的值代入表达式中,计算出结果
2;二次项系数不能为
0,而一次项系数、常
2二次函数的图象与性质
数项可以为0;函数的
表达式是整式
1二次函数y=ar和y=a(x-h)2+k的图象与性质
y=ax2
y=a(x-h)2+k
y个x=h
图象
0xo
a>0a<0
a>0
a<0
个y
a>0,开口向上,并向上无限延伸;
开口方向
a<0,开口向下,并向下无限延伸
1y=-2x2
开口大小
|a越大,开口越小;a越小,开口越大
对称轴
直线x=0(y轴)
直线x=h
★喷泉喷出的水柱类似
顶点坐标
(0,0)
(h,k)
于抛物线形状
x>0时,即在对称轴的右
x>h时,即在对称轴的右侧,y
侧,y的值随x值的增大而
的值随x值的增大而增大
增大(a>0时)或减小(a<0
最高点
(a>0时)或减小(a<0时)
时)
增减性
x<0时,即在对称轴的左
x
的值随x值的增大而减小
减小(a>0时)或增大(a<0
(a>0时)或增大(a<0时)
时)
★投篮时,篮球的运动轨
a>0时,二次函数有最小a>0时,二次函数有最小值,
迹类似于抛物线形状.
值,即当x=0时,y小值=0;
即当x=h时,y最小值=k;
最值
a<0时,二次函数有最大
a<0时,二次函数有最大值,
值,即当x=0时,y最大值=0
即当x=h时,y最大值=k
143
九年级下
典例(泰安中考)对于抛物线)=子x+1)43,下列结论:①抛物线的
开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3)④x>-1时,y随
x的增大而减小.其中正确结论的个数为(
).
a>0,c<0a<0,c>0
A.1
B.2
C.3
D.4
★抛物线y=ax2+bx+c(a≠
解折:郑物线+13中,a=
20,故开口向下,①正确」
0)与y轴交点在x轴上
方(即交于y轴正半
对称轴为直线x=-1,②错误,
轴)时,c>0;反之,c<0.
顶,点坐标为(-1,3),③正确
故可记为“a看开口,c
当x>-1时,y随x的增大而减小,④正确.综上,①③④正确
看截距”
答案:C
2二次函数y=ax2+b.x+c的图象与性质
函数
y=ax2+bx+c(a,b,c是常数,a≠0)
类别
a>0
a<0
>
b
b
对称轴在左边,
2a
X=一
↑y
2a
图象
0
咱俩同号.
★、
<0→6>09a,b
开口方向
2a
2a
向上
向下
同号.
b
对称轴
直线x=
2a
b 4ac-b2
顶点坐标
2a'
4a
当x<-
时,y的值随x值的
当x<
b
2a
时,y的值随x值的
2a
00
增减性
增大而减小;当>
b
时,y
2a
增大而增大;当x>
时,y
2a
的值随x值的增大而增大
的值随x值的增大而减小
6<0
b
最值
当x=
4ac-b2
b
时,y最小值
当x=
4ac-b2
2a
Aa
时,y最大值
2a
Aa
对称轴在右边,
b
咱俩异号
因为抛物线y=ax2+bx+c的对称轴为直线x=
,当对称轴在y轴左
2a
0,即会0,所以a与6同号:反之与6异号,放可记为
一
b
0户
侧时,一
a
b<0→a,b
异号
“左边同号,右边异号(a与b)”
144
同课章节目录
