【学霸秘籍】八(上) 第1章 勾股定理-北师大版数学-尖子生创优课堂笔记(pdf版)
文档属性
| 名称 | 【学霸秘籍】八(上) 第1章 勾股定理-北师大版数学-尖子生创优课堂笔记(pdf版) | 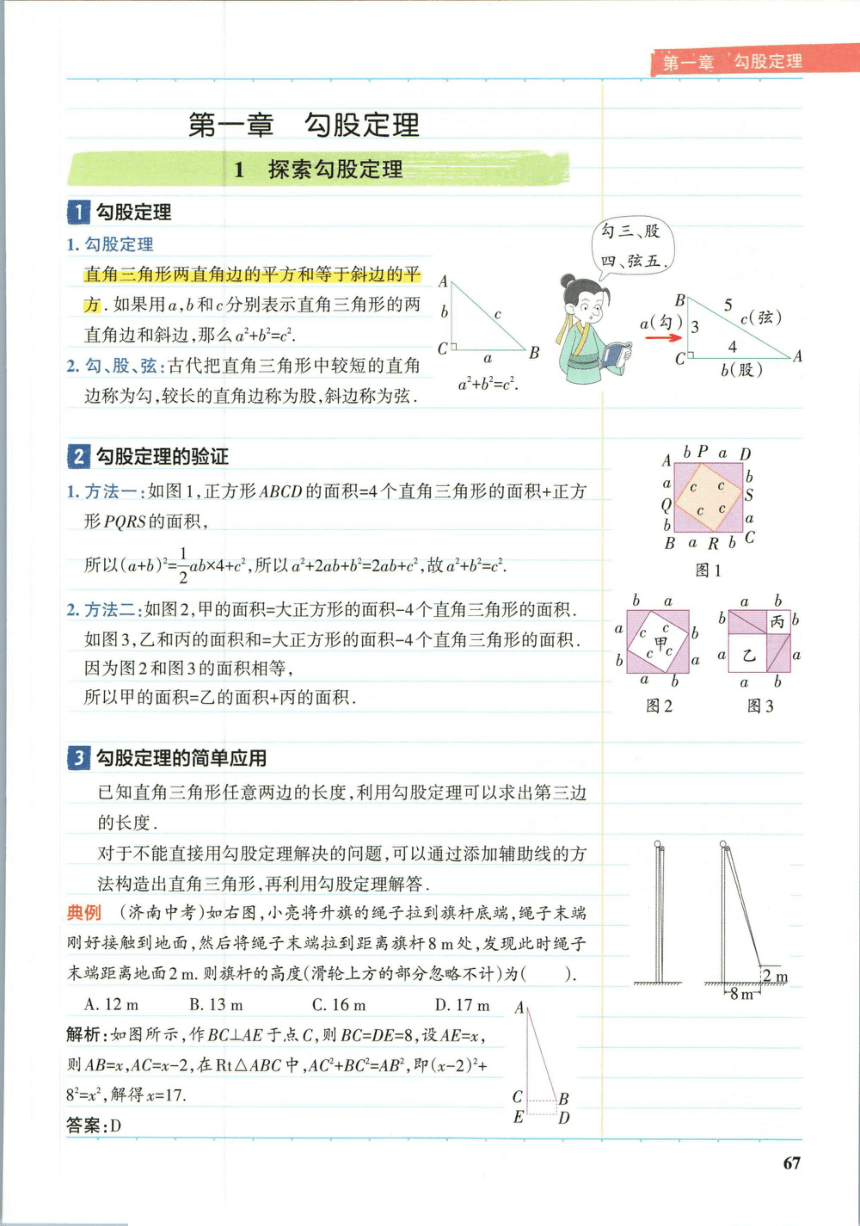 | |
| 格式 | |||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 14:59:21 | ||
图片预览

文档简介
第一章勾股定理
第一章
勾股定理
1探索勾股定理
1勾股定理
勾三、股
1.勾股定理
四、弦五,
直角三角形两直角边的平方和等于斜边的平
A
方.如果用a,b和c分别表示直角三角形的两
B
6
5
a(勾)3
c(弦)》
直角边和斜边,那么a2+b2=c2
2.勾、股、弦:古代把直角三角形中较短的直角
a
ch
A
b(股)
a2+b2=c2.
边称为勾,较长的直角边称为股,斜边称为弦
2勾股定理的验证
A
bP a D
a
cc
6
1.方法一:如图1,正方形ABCD的面积=4个直角三角形的面积+正方
Q
形PQRS的面积,
b
e
所以(a+6)rab4+e,所以+2ab+h=2atc.,故+=d
B a R b C
图1
2.方法二:如图2,甲的面积=大正方形的面积-4个直角三角形的面积.
a
a
b
b
丙b
C
如图3,乙和丙的面积和=大正方形的面积-4个直角三角形的面积
甲
6
因为图2和图3的面积相等,
6
6
a
所以甲的面积=乙的面积+丙的面积.
图2
图3
3勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边
的长度
对于不能直接用勾股定理解决的问题,可以通过添加辅助线的方
法构造出直角三角形,再利用勾股定理解答
典例(济南中考)如右图,小亮将升旗的绳子拉到旗杆底端,绳子末端
刚好接触到地面,然后将绳子末端拉到距离旗杆8处,发现此时绳子
末端距离地面2m.则旗杆的高度(滑轮上方的部分忽略不计)为(
29
A.12m
B.13m
C.16m
D.17m
解析:如图所示,作BC⊥AE于点C,则BC=DE=8,设AE=x,
则AB=x,AC=x-2,在Rt△ABC中,AC+BC=AB2,即(x-2)2+
82=x2,解得x=17.
答案:D
E
D
67
八年级上
2一定是直角三角形吗
1直角三角形的判别条件及步骤
这是个直角三角形,
1.直角三角形的判别条件(勾股定理的逆定理)
我治水时就用这个
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三
A
角形是直角三角形.如图,在△ABC中,如果AC+BC
(1)(13)
(12)
=AB,那么△ABC就是以∠C为直角的直角三角形
(2)
a
(11)
2.判断直角三角形的步骤
(3)
(10)
(9)
(4)00
。确定最大边并算出最大边的平方与另两边的平方和;
-00
(5)(6)(7)(8
。比较最大边的平方与另两边的平方和是否相等,若相等,则说明
★相传,我国古代大禹治
是直角三角形,否则,不是直角三角形
水测量工程时,也用类
典例(滨州中考)下列四组线段中,可以构成直角三角形的是(
似的方法确定直角」
A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.1,V2,3
解析:只有选项B中,两较短线段的平方和等于最长线段的平方,即
1.52+2=2.52,所以选项B中的三条线段可以构成直角三角形.
答案:B
★由定义可知,一组数是
勾股数必须满足两个
2勾股数
条件:一是满足a2+b2=
1.定义:满足a2+b2=c2的三个正整数称为勾股数
c2;二是都是正整数,
2.常见的勾股数有:3,4,5;6,8,10:5,12,13;7,24,25;8,15,17;9,12,15
二者缺一不可.
3勾股定理的应用
置立体图形上两点间的最短距离
1.求立体图形中最短路线的问题,通常是将立体图形展开,转
B自
B
化为平面图形,或者将曲面转化为平面,然后运用“两点之
侧面
间,线段最短”,并结合勾股定理求解
A
展开图
2.圆柱的侧面展开图是一个长方形,过圆柱上底面圆周上任
★蚂蚁要吃到蜂蜜的最
一点沿着侧面作一条垂直于下底面的线段,沿着这条线段剪开圆
短路线长是圆柱的侧
柱,然后展开侧面,即得到一个长方形,然后依据“两点之间,线段最
面展开图中线段AB的
短”,以最短路线为边构造直角三角形,利用勾股定理求解
长度
3.棱柱的侧面展开图是一个长方形,沿着棱柱的任意一条侧棱剪开,
它的侧面展开图是长方形,然后构造直角三角形,利用勾股定理解
决问题
68
第一章
勾股定理
1探索勾股定理
1勾股定理
勾三、股
1.勾股定理
四、弦五,
直角三角形两直角边的平方和等于斜边的平
A
方.如果用a,b和c分别表示直角三角形的两
B
6
5
a(勾)3
c(弦)》
直角边和斜边,那么a2+b2=c2
2.勾、股、弦:古代把直角三角形中较短的直角
a
ch
A
b(股)
a2+b2=c2.
边称为勾,较长的直角边称为股,斜边称为弦
2勾股定理的验证
A
bP a D
a
cc
6
1.方法一:如图1,正方形ABCD的面积=4个直角三角形的面积+正方
Q
形PQRS的面积,
b
e
所以(a+6)rab4+e,所以+2ab+h=2atc.,故+=d
B a R b C
图1
2.方法二:如图2,甲的面积=大正方形的面积-4个直角三角形的面积.
a
a
b
b
丙b
C
如图3,乙和丙的面积和=大正方形的面积-4个直角三角形的面积
甲
6
因为图2和图3的面积相等,
6
6
a
所以甲的面积=乙的面积+丙的面积.
图2
图3
3勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边
的长度
对于不能直接用勾股定理解决的问题,可以通过添加辅助线的方
法构造出直角三角形,再利用勾股定理解答
典例(济南中考)如右图,小亮将升旗的绳子拉到旗杆底端,绳子末端
刚好接触到地面,然后将绳子末端拉到距离旗杆8处,发现此时绳子
末端距离地面2m.则旗杆的高度(滑轮上方的部分忽略不计)为(
29
A.12m
B.13m
C.16m
D.17m
解析:如图所示,作BC⊥AE于点C,则BC=DE=8,设AE=x,
则AB=x,AC=x-2,在Rt△ABC中,AC+BC=AB2,即(x-2)2+
82=x2,解得x=17.
答案:D
E
D
67
八年级上
2一定是直角三角形吗
1直角三角形的判别条件及步骤
这是个直角三角形,
1.直角三角形的判别条件(勾股定理的逆定理)
我治水时就用这个
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三
A
角形是直角三角形.如图,在△ABC中,如果AC+BC
(1)(13)
(12)
=AB,那么△ABC就是以∠C为直角的直角三角形
(2)
a
(11)
2.判断直角三角形的步骤
(3)
(10)
(9)
(4)00
。确定最大边并算出最大边的平方与另两边的平方和;
-00
(5)(6)(7)(8
。比较最大边的平方与另两边的平方和是否相等,若相等,则说明
★相传,我国古代大禹治
是直角三角形,否则,不是直角三角形
水测量工程时,也用类
典例(滨州中考)下列四组线段中,可以构成直角三角形的是(
似的方法确定直角」
A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.1,V2,3
解析:只有选项B中,两较短线段的平方和等于最长线段的平方,即
1.52+2=2.52,所以选项B中的三条线段可以构成直角三角形.
答案:B
★由定义可知,一组数是
勾股数必须满足两个
2勾股数
条件:一是满足a2+b2=
1.定义:满足a2+b2=c2的三个正整数称为勾股数
c2;二是都是正整数,
2.常见的勾股数有:3,4,5;6,8,10:5,12,13;7,24,25;8,15,17;9,12,15
二者缺一不可.
3勾股定理的应用
置立体图形上两点间的最短距离
1.求立体图形中最短路线的问题,通常是将立体图形展开,转
B自
B
化为平面图形,或者将曲面转化为平面,然后运用“两点之
侧面
间,线段最短”,并结合勾股定理求解
A
展开图
2.圆柱的侧面展开图是一个长方形,过圆柱上底面圆周上任
★蚂蚁要吃到蜂蜜的最
一点沿着侧面作一条垂直于下底面的线段,沿着这条线段剪开圆
短路线长是圆柱的侧
柱,然后展开侧面,即得到一个长方形,然后依据“两点之间,线段最
面展开图中线段AB的
短”,以最短路线为边构造直角三角形,利用勾股定理求解
长度
3.棱柱的侧面展开图是一个长方形,沿着棱柱的任意一条侧棱剪开,
它的侧面展开图是长方形,然后构造直角三角形,利用勾股定理解
决问题
68
同课章节目录
