湘教版七上数学第4章图形的认识复习课件(共26张PPT)
文档属性
| 名称 | 湘教版七上数学第4章图形的认识复习课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 414.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 17:42:10 | ||
图片预览



文档简介
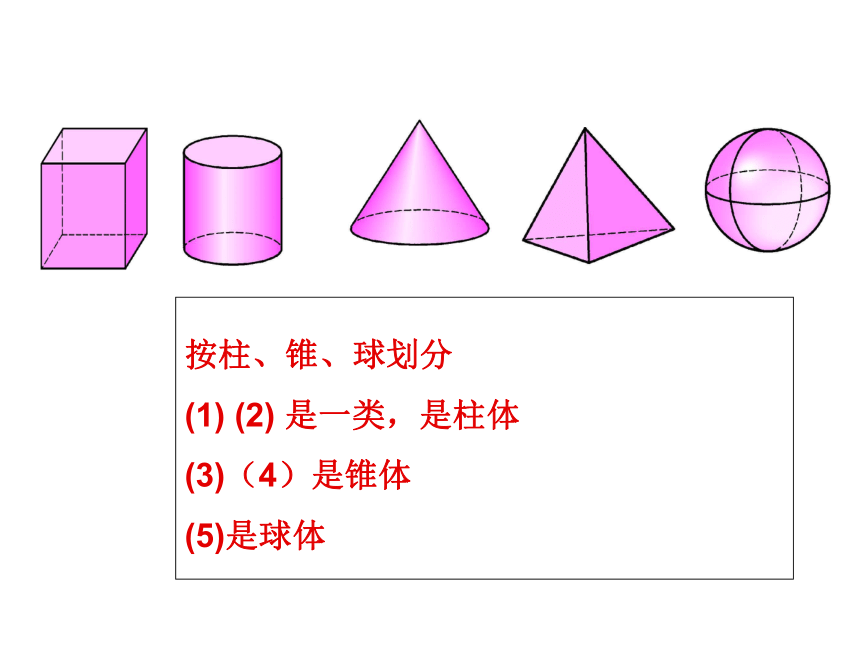
课件26张PPT。 (复习课)第四章 图形的认识按柱、锥、球划分
(1) (2) 是一类,是柱体
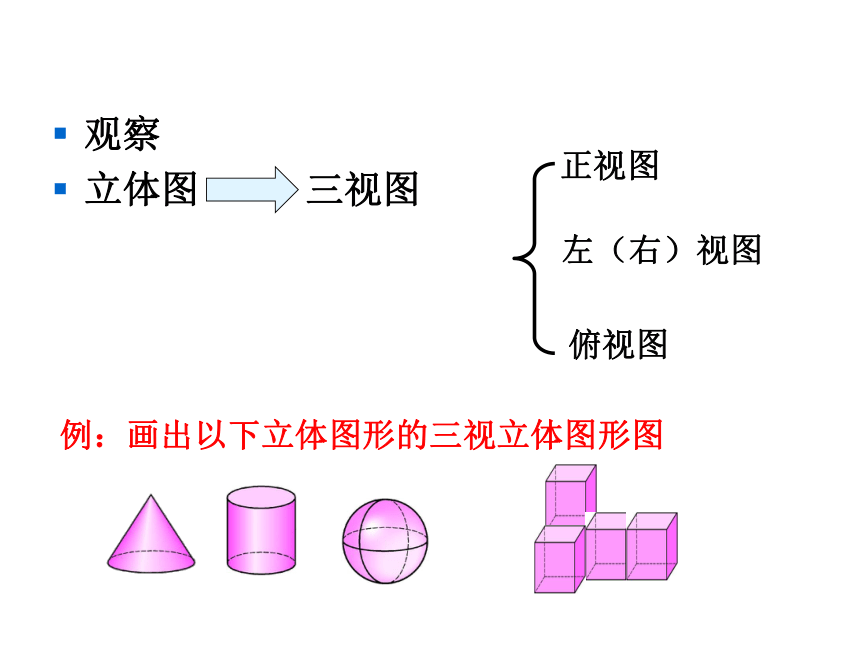
(3)(4)是锥体 (5)是球体观察
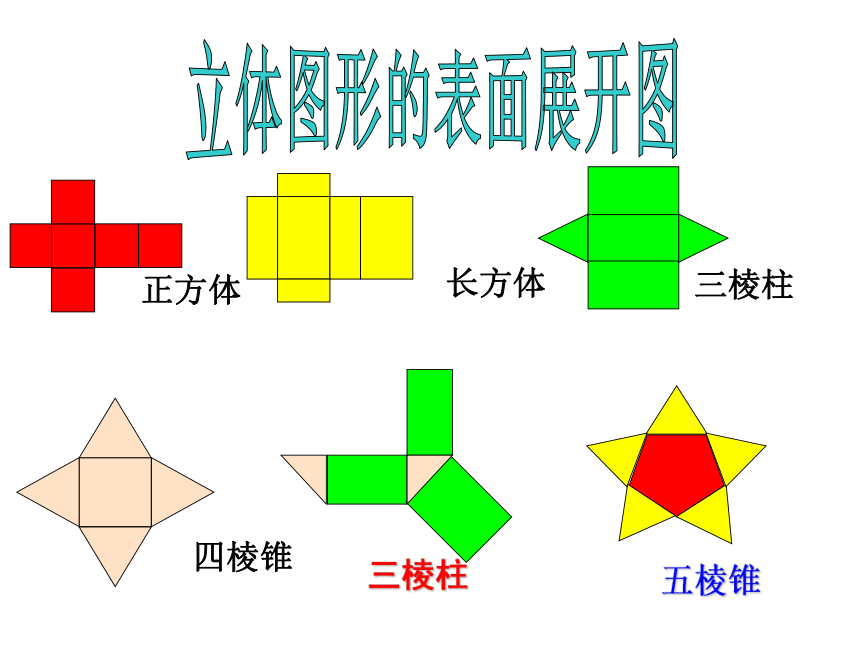
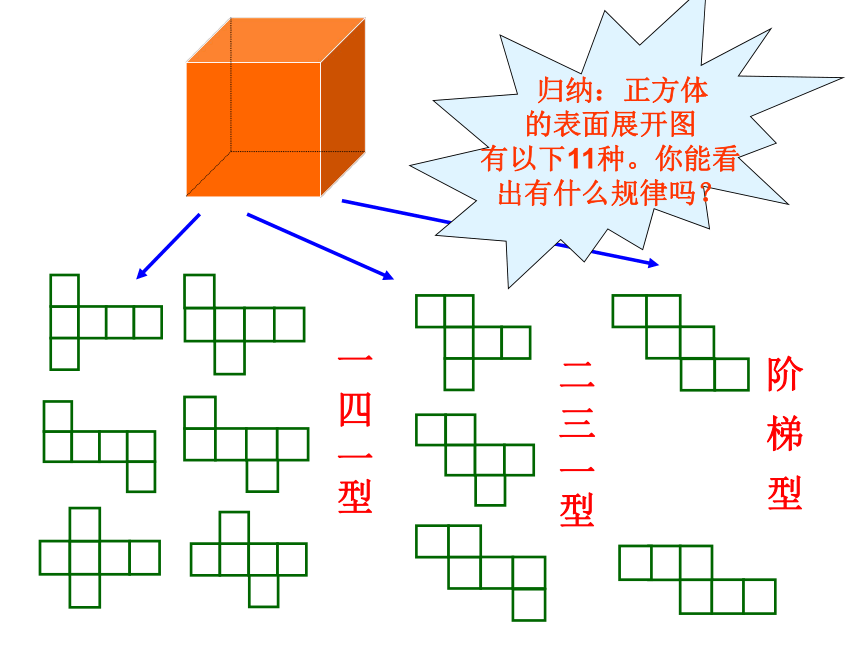
立体图 三视图正视图左(右)视图俯视图例:画出以下立体图形的三视立体图形图立体图形的表面展开图正方体长方体四棱锥三棱柱三棱柱五棱锥 归纳:正方体
的表面展开图
有以下11种。你能看
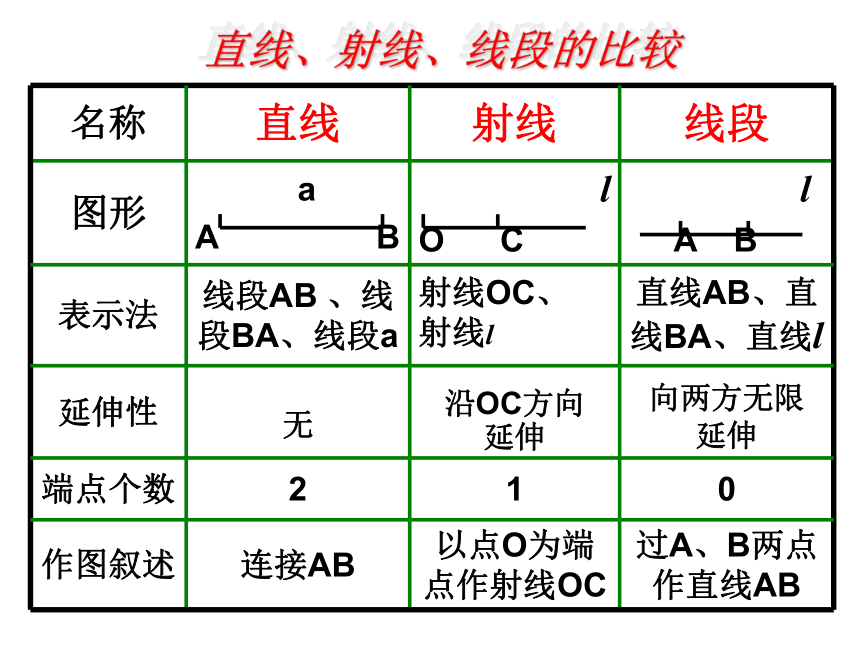
出有什么规律吗?一 四 一型二 三 一型阶 梯 型点和线A 点A ——用一个大写字母表示。 线线段直线射线学会区分没有直线、射线、线段的比较下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
下面的知识点你掌握了吗?知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明 ;用两个钉子把细木条钉在木板上,就能固定细木条,这说明________________。4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB过一点有无数条直线两点确定一条直线有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?线段的长短比较1 度量法2 叠合法3 线段中点的定义和简单作法。角用一个大写字母表示点,用二个大写字母表示线,用三个大写字母表示角,角度的转化:
1°=60′ 1′=60 〞
1°=3600 〞
角度的加减:
1.同种形式相加减;
2.度加(减)度;分加(减)分;
秒加(减)秒
3.超60进一;减一成60角的比较2 叠合法1 度量法∠ABC=∠DEF∠ABC<∠DEF∠ABC>∠DEF角的平分线1、定义:一条射线把一个角分成两个相等
的角, 这条射线叫做这个角的平分线. 2、几何语言表达:∵ OC是∠AOB的平分线OABC12∴∠1=∠2= ∠AOB
或∠AOB=2∠1=2∠21角的特殊关系 2、∠1与∠2互补,∠1是∠2的补角,∠2是∠1的补角.∠1+∠2=180 °1、∠1与∠2互余,∠1是∠2的余角,∠2是∠1的余角.∠1+∠2=90 °1)两个角成对出现2)只考虑数量关系,与位置无关.结论: 同角(等角)的余角(补角)相等 注意!方位角:1、方位角是以正南、正北方向为基准,描述物体的运动方向。
2、北偏东45 °通常叫做东北方向,北偏西45 °通常叫做西北方向,南偏东45 °通常叫做东南方向,南偏西45 °通常叫做西南方向。
3、方位角在航行、测绘等实际生活中的应用十分广泛。OA练习、在右图中画出表示下列方向的射线:
(1)北偏西30 °(2)北偏东50 °
(3)西南方向
立体图 三视图正视图左(右)视图俯视图例:画出以下立体图形的三视立体图形图立体图形的表面展开图正方体长方体四棱锥三棱柱三棱柱五棱锥 归纳:正方体
的表面展开图
有以下11种。你能看
出有什么规律吗?一 四 一型二 三 一型阶 梯 型点和线A 点A ——用一个大写字母表示。 线线段直线射线学会区分没有直线、射线、线段的比较下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
下面的知识点你掌握了吗?知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明 ;用两个钉子把细木条钉在木板上,就能固定细木条,这说明________________。4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB过一点有无数条直线两点确定一条直线有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?线段的长短比较1 度量法2 叠合法3 线段中点的定义和简单作法。角用一个大写字母表示点,用二个大写字母表示线,用三个大写字母表示角,角度的转化:
1°=60′ 1′=60 〞
1°=3600 〞
角度的加减:
1.同种形式相加减;
2.度加(减)度;分加(减)分;
秒加(减)秒
3.超60进一;减一成60角的比较2 叠合法1 度量法∠ABC=∠DEF∠ABC<∠DEF∠ABC>∠DEF角的平分线1、定义:一条射线把一个角分成两个相等
的角, 这条射线叫做这个角的平分线. 2、几何语言表达:∵ OC是∠AOB的平分线OABC12∴∠1=∠2= ∠AOB
或∠AOB=2∠1=2∠21角的特殊关系 2、∠1与∠2互补,∠1是∠2的补角,∠2是∠1的补角.∠1+∠2=180 °1、∠1与∠2互余,∠1是∠2的余角,∠2是∠1的余角.∠1+∠2=90 °1)两个角成对出现2)只考虑数量关系,与位置无关.结论: 同角(等角)的余角(补角)相等 注意!方位角:1、方位角是以正南、正北方向为基准,描述物体的运动方向。
2、北偏东45 °通常叫做东北方向,北偏西45 °通常叫做西北方向,南偏东45 °通常叫做东南方向,南偏西45 °通常叫做西南方向。
3、方位角在航行、测绘等实际生活中的应用十分广泛。OA练习、在右图中画出表示下列方向的射线:
(1)北偏西30 °(2)北偏东50 °
(3)西南方向
同课章节目录
