湘教七上数学第2章 代数式第3节《代数式的值》参考课件(共31张PPT)
文档属性
| 名称 | 湘教七上数学第2章 代数式第3节《代数式的值》参考课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 671.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 18:47:47 | ||
图片预览











文档简介
课件31张PPT。2.3 代数式的值1.理解代数式的值的含义.
2.会求代数式的值.(重点、难点)一、代数式的值
人民商场2013年4月份的营业额为a万元,5月份的营业额比4月
份的2倍少10万元,用含a的代数式表示5月份的营业额为
________(万元).
当a=300万元时,5月份的营业额为___________=_____(万元).(2a-10)2×300-10590当a=350万元,5月份的营业额为__________=690 (万元).
把590和690分别叫做代数式2a-10当a=300和a=350时的值.
【总结】如果把代数式里的字母用___代入,那么计算后得出
的_____叫做代数式的值.
二、计算代数式的值的步骤
1._____.2._____得值.2×350-10数结果代入计算 (打“√”或“×”)
(1)当a=2时,2a+1=5,故代数式2a+1的值是5.( )
(2)在圆的面积公式S=πR2中,R可以取任意数.( )
(3)若a+b=5,则代数式a+b-1的值为4.( )
(4)当x=2时,代数式3x+6的值为24.( )
(5)不论x取何值,代数式2x2+1的值总为正数.( )××√×√知识点 1 求代数式的值
【例1】(1)当x=7,y=4,z=0时,求代数式x(2x-y+3z)的值.
(2)若3a+2b=5,求6a+4b-8的值.
【思路点拨】(1)代入→求值→结果
(2)变形6a+4b-8→整体代入→求值【自主解答】(1)当x=7,y=4,z=0时,
x(2x-y+3z)=7×(2×7-4+3×0)
=7×(14-4)=7×10=70.
(2)6a+4b-8=2(3a+2b)-8.
当3a+2b=5时,原式=2×5-8=2.【总结提升】代数式求值的两种类型及方法
1.直接代入求值.
方法:把代数式里相应字母的值代入,然后按照代数式的运算顺序进行计算.
2.整体代入求值.
方法:(1)直接整体代入:如a-b=3,求a-b+2,直接将a-b=3代入得a-b+2=3+2=5.
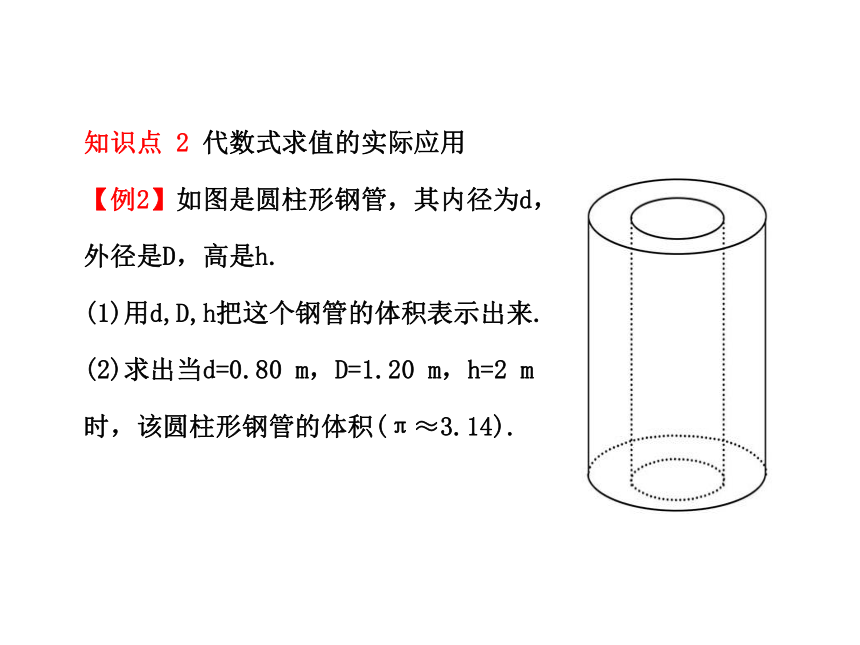
(2)变形后整体代入:即对已知变形后方可代入或有时要对已知和被求代数式都变形才能整体代入求解.知识点 2 代数式求值的实际应用
【例2】如图是圆柱形钢管,其内径为d,
外径是D,高是h.
(1)用d,D,h把这个钢管的体积表示出来.
(2)求出当d=0.80 m,D=1.20 m,h=2 m
时,该圆柱形钢管的体积(π≈3.14).【解题探究】(1)圆柱体的体积公式是什么?
提示:底面积×高,即V=πr2h.
(2)如何计算空心圆柱(即钢管)的体积?
提示:外面大圆柱的体积-里面小圆柱的体积.
(3)如何表示钢管的体积?
提示:(4)如何求出钢管体积的具体值?
提示:代入求值.
当d=0.80 m,D=1.20 m,h=2 m时,
≈
=1.256(m3).【互动探究】这个圆柱形钢管的表面积如何表示?
提示:【总结提升】应用列代数式求值的“三步法”题组一:求代数式的值
1.当a=5时,下列代数式的值最大的是( )
A.2a+3 B. a-1
C. a2-1 D.5(a-1)
【解析】选D.把a=5分别代入得2a+3=2×5+3=13;
5(a-1)=5×4=20.2.根据如图所示的运算流程计算y的值,若输入的x的值为 ,
则输出的y值为( )A. B. C. D.
【解析】选B.因为2< <4,所以当x= 时,输出的y值为 .3.如表表示每给一个x值,得到某个代数式的相应值,满足表中所列条件的代数式是( )
A.x+2 B.2x-3
C.3x-10 D.-3x+2
【解析】选D.把x=0,1,2,3代入A,B,C,D的式子进行验证.4.若(x+1)2与|y-2|互为相反数,则(x+y)2 013的值为______.
【解析】由题意知,(x+1)2+|y-2|=0,
所以x+1=0,y-2=0,
所以x=-1,y=2,
所以(x+y)2 013=(-1+2)2 013=1.
答案:15.(2012·泰州中考)若2a-b=5,则6a-3b的值是______.
【解析】因为2a-b=5,
所以6a-3b=3(2a-b)=3×5=15.
答案:156.已知a3-a-1=0,则a3-a+2 013=______.
【解析】因为a3-a-1=0,
所以a3-a=1.
故a3-a+2 013=1+2 013= 2 014.
答案:2 0147.(2012·河北中考)已知y=x-1,则(x-y)2+(y-x)+1的值为______.
【解析】由y=x-1得y-x=-1,
所以(x-y)2+(y-x)+1=(y-x)2+(y-x)+1
=(-1)2+(-1)+1=1.
答案:18.求代数式的值:4x2+3xy-x2-9,其中x=2,y=-3.
【解析】当x=2,y=-3时,
原式=4×22+3×2×(-3)-22-9=4×4+3×2×(-3)-22-9=-15.题组二:代数式求值的实际应用
1.在梯形面积公式S= (a+b)h中,若已知S=20,h=4,a=4,
则b=______.
【解析】把S=20,h=4,a=4代入S= (a+b)h,
得20= (4+b)×4,
即20=2(4+b),
所以4+b=10,
所以b=6.
答案:62.在足球比赛中,n个球队进行单循环赛比赛的总场次为
n(n-1),若有6个队参加比赛,则比赛的总场次为______.
【解析】把n=6代入 n(n-1)得: ×6×(6-1)=15.
答案:153.三个植树队,第一队种树x棵,第二队种的树比第一队种的树的2倍少26棵,第三队种的树比第二队种的树的一半多42棵,三个队一共种树多少棵?当x=100时,三个队共种树多少棵?【解析】第二队种树(2x-26)棵,
第三队种树[ (2x-26)+42]棵.
三个队一共种树:
x+(2x-26)+[ (2x-26)+42]
=x+2x-26+x-13+42
=(1+2+1)x+(-26-13+42)=(4x+3)(棵).
当x=100时,三个队共种树4×100+3=403(棵).4.某人先步行了S0 km,后搭乘速度为v km/h的汽车,走了t h.
(1)问该人共走了多少路程?
(2)若S0=3,v=40,t=0.3,所走的路程是多少千米?
【解析】(1)根据公式S=vt可得,该人共走的路程为S0+vt.
(2)当S0=3,v=40,t=0.3时,
S0+vt=3+40×0.3=15(km).5.有总长为a的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为x.
(1)用关于a,x的代数式表示园子的面积.
(2)当a=100 m,x=20 m时,求园子的面积.【解析】(1)园子的长为(a-2x)m,
所以其面积为x(a-2x)m2.
(2)当a=100 m,x=20 m时,
x(a-2x)=20×(100-2×20)=1 200 (m2).6.科学家在研究地震活动规律时发现,古地震发生至今的间隔
年代y与震区古树木树干茎部的周长c和树木年轮平均生长宽度
d之间有一个关系式 若科学家在2012年测得某震区一
古树木的树干茎部的周长c=264 cm,它的年轮平均生长宽度
d=0.66 mm,请你计算一下该震区地震发生的大致年代.
【解析】c=264 cm=2 640 mm,
y≈ ≈637(年),2 012-637=1 375.
所以该地区地震发生的大致年代是1375年. 【想一想错在哪?】当x=2时,代数式ax3+bx+5的值为8,那么当x=-2时,代数式ax3+bx+5的值为多少?
提示:代数式ax3+bx+5中的5是不变的.
2.会求代数式的值.(重点、难点)一、代数式的值
人民商场2013年4月份的营业额为a万元,5月份的营业额比4月
份的2倍少10万元,用含a的代数式表示5月份的营业额为
________(万元).
当a=300万元时,5月份的营业额为___________=_____(万元).(2a-10)2×300-10590当a=350万元,5月份的营业额为__________=690 (万元).
把590和690分别叫做代数式2a-10当a=300和a=350时的值.
【总结】如果把代数式里的字母用___代入,那么计算后得出
的_____叫做代数式的值.
二、计算代数式的值的步骤
1._____.2._____得值.2×350-10数结果代入计算 (打“√”或“×”)
(1)当a=2时,2a+1=5,故代数式2a+1的值是5.( )
(2)在圆的面积公式S=πR2中,R可以取任意数.( )
(3)若a+b=5,则代数式a+b-1的值为4.( )
(4)当x=2时,代数式3x+6的值为24.( )
(5)不论x取何值,代数式2x2+1的值总为正数.( )××√×√知识点 1 求代数式的值
【例1】(1)当x=7,y=4,z=0时,求代数式x(2x-y+3z)的值.
(2)若3a+2b=5,求6a+4b-8的值.
【思路点拨】(1)代入→求值→结果
(2)变形6a+4b-8→整体代入→求值【自主解答】(1)当x=7,y=4,z=0时,
x(2x-y+3z)=7×(2×7-4+3×0)
=7×(14-4)=7×10=70.
(2)6a+4b-8=2(3a+2b)-8.
当3a+2b=5时,原式=2×5-8=2.【总结提升】代数式求值的两种类型及方法
1.直接代入求值.
方法:把代数式里相应字母的值代入,然后按照代数式的运算顺序进行计算.
2.整体代入求值.
方法:(1)直接整体代入:如a-b=3,求a-b+2,直接将a-b=3代入得a-b+2=3+2=5.
(2)变形后整体代入:即对已知变形后方可代入或有时要对已知和被求代数式都变形才能整体代入求解.知识点 2 代数式求值的实际应用
【例2】如图是圆柱形钢管,其内径为d,
外径是D,高是h.
(1)用d,D,h把这个钢管的体积表示出来.
(2)求出当d=0.80 m,D=1.20 m,h=2 m
时,该圆柱形钢管的体积(π≈3.14).【解题探究】(1)圆柱体的体积公式是什么?
提示:底面积×高,即V=πr2h.
(2)如何计算空心圆柱(即钢管)的体积?
提示:外面大圆柱的体积-里面小圆柱的体积.
(3)如何表示钢管的体积?
提示:(4)如何求出钢管体积的具体值?
提示:代入求值.
当d=0.80 m,D=1.20 m,h=2 m时,
≈
=1.256(m3).【互动探究】这个圆柱形钢管的表面积如何表示?
提示:【总结提升】应用列代数式求值的“三步法”题组一:求代数式的值
1.当a=5时,下列代数式的值最大的是( )
A.2a+3 B. a-1
C. a2-1 D.5(a-1)
【解析】选D.把a=5分别代入得2a+3=2×5+3=13;
5(a-1)=5×4=20.2.根据如图所示的运算流程计算y的值,若输入的x的值为 ,
则输出的y值为( )A. B. C. D.
【解析】选B.因为2< <4,所以当x= 时,输出的y值为 .3.如表表示每给一个x值,得到某个代数式的相应值,满足表中所列条件的代数式是( )
A.x+2 B.2x-3
C.3x-10 D.-3x+2
【解析】选D.把x=0,1,2,3代入A,B,C,D的式子进行验证.4.若(x+1)2与|y-2|互为相反数,则(x+y)2 013的值为______.
【解析】由题意知,(x+1)2+|y-2|=0,
所以x+1=0,y-2=0,
所以x=-1,y=2,
所以(x+y)2 013=(-1+2)2 013=1.
答案:15.(2012·泰州中考)若2a-b=5,则6a-3b的值是______.
【解析】因为2a-b=5,
所以6a-3b=3(2a-b)=3×5=15.
答案:156.已知a3-a-1=0,则a3-a+2 013=______.
【解析】因为a3-a-1=0,
所以a3-a=1.
故a3-a+2 013=1+2 013= 2 014.
答案:2 0147.(2012·河北中考)已知y=x-1,则(x-y)2+(y-x)+1的值为______.
【解析】由y=x-1得y-x=-1,
所以(x-y)2+(y-x)+1=(y-x)2+(y-x)+1
=(-1)2+(-1)+1=1.
答案:18.求代数式的值:4x2+3xy-x2-9,其中x=2,y=-3.
【解析】当x=2,y=-3时,
原式=4×22+3×2×(-3)-22-9=4×4+3×2×(-3)-22-9=-15.题组二:代数式求值的实际应用
1.在梯形面积公式S= (a+b)h中,若已知S=20,h=4,a=4,
则b=______.
【解析】把S=20,h=4,a=4代入S= (a+b)h,
得20= (4+b)×4,
即20=2(4+b),
所以4+b=10,
所以b=6.
答案:62.在足球比赛中,n个球队进行单循环赛比赛的总场次为
n(n-1),若有6个队参加比赛,则比赛的总场次为______.
【解析】把n=6代入 n(n-1)得: ×6×(6-1)=15.
答案:153.三个植树队,第一队种树x棵,第二队种的树比第一队种的树的2倍少26棵,第三队种的树比第二队种的树的一半多42棵,三个队一共种树多少棵?当x=100时,三个队共种树多少棵?【解析】第二队种树(2x-26)棵,
第三队种树[ (2x-26)+42]棵.
三个队一共种树:
x+(2x-26)+[ (2x-26)+42]
=x+2x-26+x-13+42
=(1+2+1)x+(-26-13+42)=(4x+3)(棵).
当x=100时,三个队共种树4×100+3=403(棵).4.某人先步行了S0 km,后搭乘速度为v km/h的汽车,走了t h.
(1)问该人共走了多少路程?
(2)若S0=3,v=40,t=0.3,所走的路程是多少千米?
【解析】(1)根据公式S=vt可得,该人共走的路程为S0+vt.
(2)当S0=3,v=40,t=0.3时,
S0+vt=3+40×0.3=15(km).5.有总长为a的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为x.
(1)用关于a,x的代数式表示园子的面积.
(2)当a=100 m,x=20 m时,求园子的面积.【解析】(1)园子的长为(a-2x)m,
所以其面积为x(a-2x)m2.
(2)当a=100 m,x=20 m时,
x(a-2x)=20×(100-2×20)=1 200 (m2).6.科学家在研究地震活动规律时发现,古地震发生至今的间隔
年代y与震区古树木树干茎部的周长c和树木年轮平均生长宽度
d之间有一个关系式 若科学家在2012年测得某震区一
古树木的树干茎部的周长c=264 cm,它的年轮平均生长宽度
d=0.66 mm,请你计算一下该震区地震发生的大致年代.
【解析】c=264 cm=2 640 mm,
y≈ ≈637(年),2 012-637=1 375.
所以该地区地震发生的大致年代是1375年. 【想一想错在哪?】当x=2时,代数式ax3+bx+5的值为8,那么当x=-2时,代数式ax3+bx+5的值为多少?
提示:代数式ax3+bx+5中的5是不变的.
同课章节目录
