七年级数学《1.1认识三角形》学案 鲁教版五四制
文档属性
| 名称 | 七年级数学《1.1认识三角形》学案 鲁教版五四制 |
|
|
| 格式 | zip | ||
| 文件大小 | 24.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 17:25:18 | ||
图片预览

文档简介
认识三角形
学习目标: 1、掌握证明“三角形内角和等于180°”的方法,发现“直角三角形的两个锐角互余”;
2、能按角将三角形分成三类。
学习重点:三角形内角和定理推理和应用(侧重于计算)。
学习难点:三角形内角和定理推理和应用。
一、自学探究:预习课本第138—140页并完成下列各题:(你能找到答案吗?相信自己最聪明!)
1、在△ABC中,(1)∠C=70°,∠A=50°,则∠B= 度;
(2)∠B=100°,∠A=∠C,则∠C= 度
2、三角形按角分为三类:(1) 三角形(2) 三角形(3) 三角形
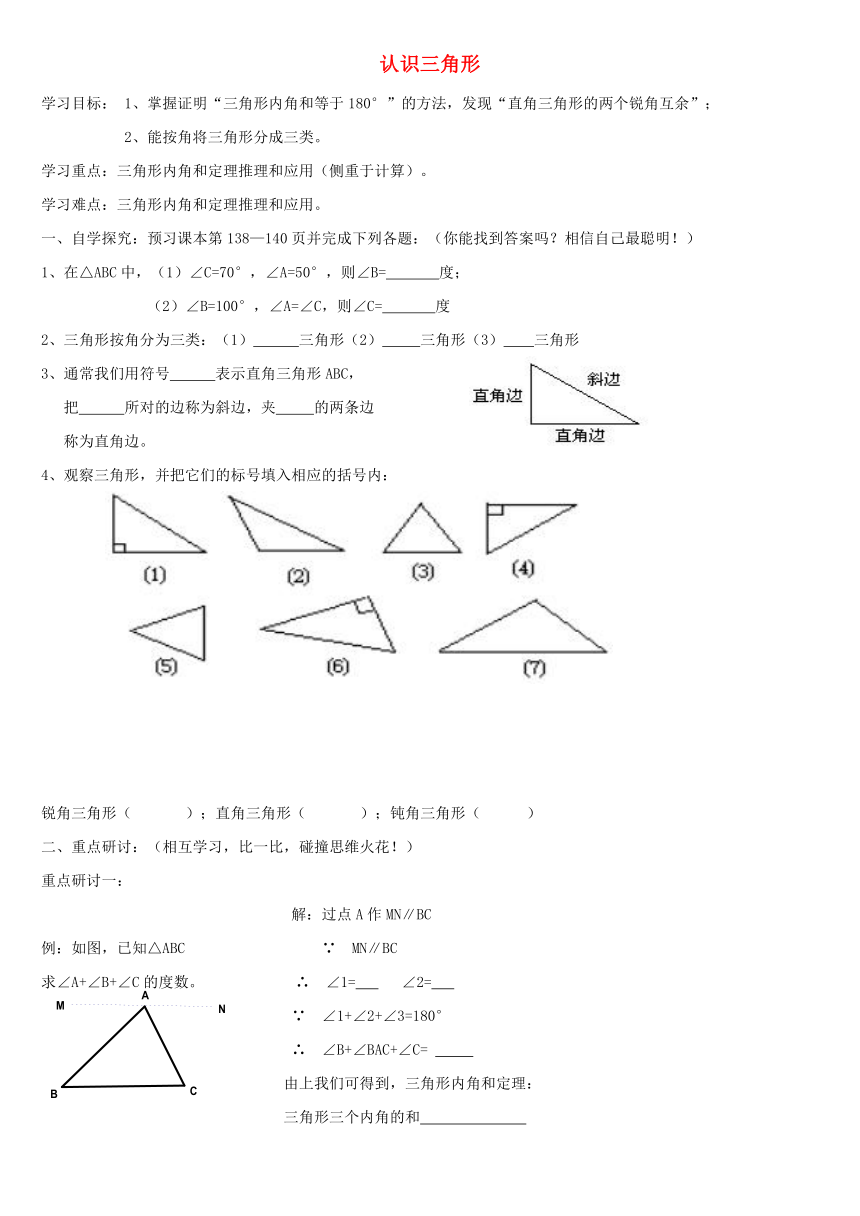
3、通常我们用符号 表示直角三角形ABC,
把 所对的边称为斜边,夹 的两条边
称为直角边。
4、观察三角形,并把它们的标号填入相应的括号内:
锐角三角形( );直角三角形( );钝角三角形( )
二、重点研讨:(相互学习,比一比,碰撞思维火花!)
重点研讨一:
解:过点A作MN∥BC
例:如图,已知△ABC ∵ MN∥BC
求∠A+∠B+∠C的度数。 ∴ ∠1= ∠2=
∵ ∠1+∠2+∠3=180°
∴ ∠B+∠BAC+∠C=
由上我们可得到,三角形内角和定理:
三角形三个内角的和
还有其他说明方法吗?
重点研讨二:
回答课本第139页猜一猜中的问题并说明你的理由。
小明所拿三角形被遮住的两个内角是什么角? 小颖的呢?
猜一猜中的第二幅图中遮住的两个内角可能是什么角? 。
一个三角形中三个内角可以是什么角?
总结:一个三角形的三个内角中,最少有 个锐角,最多有 个直角(钝角)
重点研讨三:直角三角形中的两个锐角有什么关系?结论 。
三:巩固练习:(检测自己,证明自己的实力!)
1、判断:(1)一个三角形的三个内角可以都小于60°; ( )
(2)一个三角形最多只能有一个内角是钝角或直角; ( )
2、在△ABC中, (1)∠A=80°,∠B=∠C,则∠C= 度;
(2)2∠A=∠B+∠C,则∠A= 度。
3、如右图:求△ABC各内角的度数
4、一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和60° ( ) ;(2)40°和70°( );(3)50°和30° ( )
5、在空白处填入“锐角”、“直角”或“钝角”:
如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的两个内角都小于40°,那么这个三角形是 三角形;
(3)如果三角形的一个内角等于另外两个内角之和(差),那么这个三角形是 三角形。
6、在Rt△ABC中,AB是斜边,∠A=2∠B,则∠A= 度,∠B= 度;
四:延伸迁移:(巧思妙想,勇攀高峰!)
一个零件的形状如图所示,按规定∠A应该等于90°
∠B、∠D应分别是20°和30°,李叔叔量得∠BCD=142°,
就断定这个零件不合格,你能说出其中的理由吗?
五:达标检测:(你能拿满分吗?相信你是最棒最聪明!)
1、在△ABC中,(1)∠A=∠B+∠C, 则△ABC是 三角形
(2)∠A =∠B—∠C, 则△ABC是 三角形
2、在△ABC中,∠A: ∠B: ∠C=1:2:3,则△ABC的三个内角的度数为 ;△ABC的形状是
3、三角形三个内角中,锐角最多可以是( )
A、0个 B、1个 C、2个 D、3个
4、如右图 ,∠1=60°,∠D=20°,则∠A= 度;
5 、如图,已知△ABC中,∠1=27°,∠2=85°,∠3=38°求∠4的度数
6.如右图,DF⊥AB, ∠A=55°, ∠D=50°, 则∠ACB=
板书设计:三角形的内角和
一 探索三角形的内角和(共有三种方法)
二 三角形的分类
三 直角三角形
教学反思:三角形的内角和是180°,学生很早就已经知道这个结论了,但是学生不会用几何的方法来证明,所以本节的一个重点将放在证明三角形的内角和的证明上面。
学习目标: 1、掌握证明“三角形内角和等于180°”的方法,发现“直角三角形的两个锐角互余”;
2、能按角将三角形分成三类。
学习重点:三角形内角和定理推理和应用(侧重于计算)。
学习难点:三角形内角和定理推理和应用。
一、自学探究:预习课本第138—140页并完成下列各题:(你能找到答案吗?相信自己最聪明!)
1、在△ABC中,(1)∠C=70°,∠A=50°,则∠B= 度;
(2)∠B=100°,∠A=∠C,则∠C= 度
2、三角形按角分为三类:(1) 三角形(2) 三角形(3) 三角形
3、通常我们用符号 表示直角三角形ABC,
把 所对的边称为斜边,夹 的两条边
称为直角边。
4、观察三角形,并把它们的标号填入相应的括号内:
锐角三角形( );直角三角形( );钝角三角形( )
二、重点研讨:(相互学习,比一比,碰撞思维火花!)
重点研讨一:
解:过点A作MN∥BC
例:如图,已知△ABC ∵ MN∥BC
求∠A+∠B+∠C的度数。 ∴ ∠1= ∠2=
∵ ∠1+∠2+∠3=180°
∴ ∠B+∠BAC+∠C=
由上我们可得到,三角形内角和定理:
三角形三个内角的和
还有其他说明方法吗?
重点研讨二:
回答课本第139页猜一猜中的问题并说明你的理由。
小明所拿三角形被遮住的两个内角是什么角? 小颖的呢?
猜一猜中的第二幅图中遮住的两个内角可能是什么角? 。
一个三角形中三个内角可以是什么角?
总结:一个三角形的三个内角中,最少有 个锐角,最多有 个直角(钝角)
重点研讨三:直角三角形中的两个锐角有什么关系?结论 。
三:巩固练习:(检测自己,证明自己的实力!)
1、判断:(1)一个三角形的三个内角可以都小于60°; ( )
(2)一个三角形最多只能有一个内角是钝角或直角; ( )
2、在△ABC中, (1)∠A=80°,∠B=∠C,则∠C= 度;
(2)2∠A=∠B+∠C,则∠A= 度。
3、如右图:求△ABC各内角的度数
4、一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和60° ( ) ;(2)40°和70°( );(3)50°和30° ( )
5、在空白处填入“锐角”、“直角”或“钝角”:
如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的两个内角都小于40°,那么这个三角形是 三角形;
(3)如果三角形的一个内角等于另外两个内角之和(差),那么这个三角形是 三角形。
6、在Rt△ABC中,AB是斜边,∠A=2∠B,则∠A= 度,∠B= 度;
四:延伸迁移:(巧思妙想,勇攀高峰!)
一个零件的形状如图所示,按规定∠A应该等于90°
∠B、∠D应分别是20°和30°,李叔叔量得∠BCD=142°,
就断定这个零件不合格,你能说出其中的理由吗?
五:达标检测:(你能拿满分吗?相信你是最棒最聪明!)
1、在△ABC中,(1)∠A=∠B+∠C, 则△ABC是 三角形
(2)∠A =∠B—∠C, 则△ABC是 三角形
2、在△ABC中,∠A: ∠B: ∠C=1:2:3,则△ABC的三个内角的度数为 ;△ABC的形状是
3、三角形三个内角中,锐角最多可以是( )
A、0个 B、1个 C、2个 D、3个
4、如右图 ,∠1=60°,∠D=20°,则∠A= 度;
5 、如图,已知△ABC中,∠1=27°,∠2=85°,∠3=38°求∠4的度数
6.如右图,DF⊥AB, ∠A=55°, ∠D=50°, 则∠ACB=
板书设计:三角形的内角和
一 探索三角形的内角和(共有三种方法)
二 三角形的分类
三 直角三角形
教学反思:三角形的内角和是180°,学生很早就已经知道这个结论了,但是学生不会用几何的方法来证明,所以本节的一个重点将放在证明三角形的内角和的证明上面。
