七年级上册数学《1.1认识三角形》学案 鲁教版五四制
文档属性
| 名称 | 七年级上册数学《1.1认识三角形》学案 鲁教版五四制 |

|
|
| 格式 | zip | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 17:26:53 | ||
图片预览


文档简介
认识三角形
学习目标:1、通过折纸、画图等活动,认识三角形的中线、角平分线,会用几何语言表示。
2、会画出任意三角形的中线、角平分线,通过画图了解各种三角形三条中线、角平分线的位置关系。
学习重点:会画出任意三角形的中线、角平分线,通过画图了解各种三角形三条中线、角平分线的位置关系。
自主探究:(预习课本143—144页,完成下列各题)
1、在三角形中,_______________________________,这个角的顶点与交点之间的________叫三角形的角平分线。
2、在三角形中, _______________________________,叫做这个三角形的中线.
二、重点研讨:
研讨一:请你画出锐角三角形、直角三角形、钝角三角形的所有角平分线,并且观察这些角平分线有什么规律?
一个三角形共有_______条角平分线,他们都在三角形____部,而且相交于 点。
如图:∵AD是三角形ABC的角平分线。
∴ =_______=∠BAC
或∠BAC=_______=
例题:△ABC中,∠B=800 ,∠C=400,BO、CO平分∠B、∠C,则∠BOC=________。
研讨二:请你画出锐角三角形、直角三角形、钝角三角形的所有中线,并且观察这些中线有什么规律?
一个三角形共有_______条中线,他们都在三角形____部,而且相交于 点。
如图:∵AD是三角形ABC的角平分线。
∴BD=______=_______
或:_____=2BD=_______
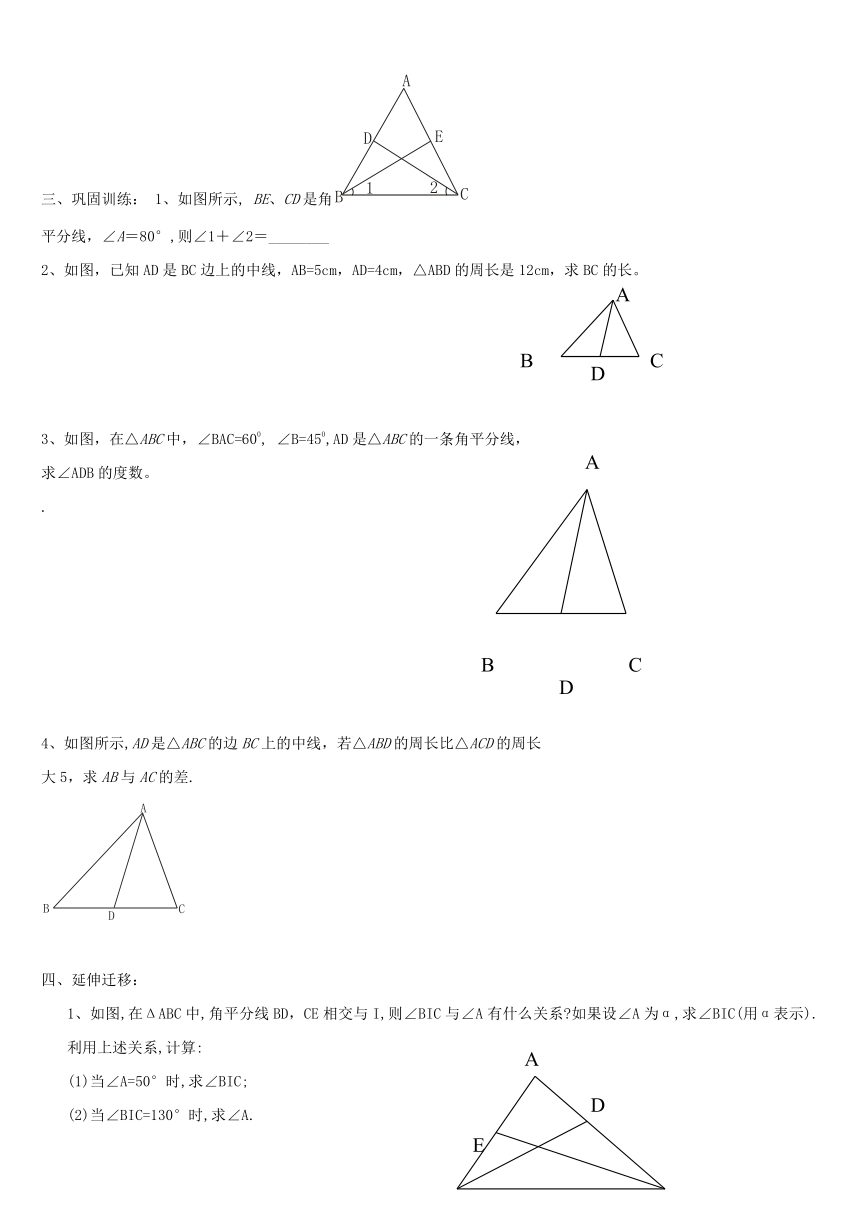
三、巩固训练: 1、如图所示, BE、CD是角
平分线,∠A=80°,则∠1+∠2=________
2、如图,已知AD是BC边上的中线,AB=5cm,AD=4cm,△ABD的周长是12cm,求BC的长。
3、如图,在△ABC中,∠BAC=600, ∠B=450,AD是△ABC的一条角平分线,
求∠ADB的度数。
.
4、如图所示,AD是△ABC的边BC上的中线,若△ABD的周长比△ACD的周长
大5,求AB与AC的差.
四、延伸迁移:
1、如图,在ΔABC中,角平分线BD,CE相交与I,则∠BIC与∠A有什么关系 如果设∠A为α,求∠BIC(用α表示).利用上述关系,计算:
(1)当∠A=50°时,求∠BIC;
(2)当∠BIC=130°时,求∠A.
2、等腰三角形一腰上的中线把该三角形的周长分别为13.5cm和11.5cm两部分。求这个等腰三角形各边长。
五、达标检测:
1、三角形的中线是( )
A、直线 B、 射线 C、 线段 D、以上答案都不对
2、已知△ABC中,∠B=∠C=50°,AD为∠BAC的平分线,则∠BAD=( )
A 40° B 45° C 50° D 55
3、已知AD是△ABC的中线,且AB=8cm. AC=5cm,则△ABD与△ACD的周长之差为 ,
4、直角三角形两锐角平分线相交所成的角的度数是
5、在△ABC中,AD是BC边上的中线,△ABC的周长比△ACD的周长多5cm,AB与AC的和为11cm,求AB的长。
5.1认识三角形(4)
学习目标:1、通过折纸、画图等活动,认识三角形的高。
2、会画出任意三角形的高(尤其是钝角三角形),通过画图了解各种三角形三条高的位置关系。
学习重点:会画出任意三角形的高,通过画图了解各种三角形三条高的位置关系。
自主探究:(预习课本145页“做一做”上面的内容)
从三角形的一个顶点向它的对边所在直线作垂线, 叫做三角形的高线,简称 。
二、重点研讨:
研讨一:如图,一个锐角△ABC,
⑴ 你能画出这个三角形的三条高吗
⑵ 每人准备一个锐角三角形纸片,你能用折纸的办法
得到它们吗 与同桌交流你的做法
⑶ 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.
研讨二:如图,一个直角△ABC。
⑴画出直角三角形的三条高,
直角边BC边上的高是 ;
直角边AB边上的高是 ;
它们有怎样的位置关系?将你的结果与同伴进行交流.
研讨三:如图,一个钝角三角形△ABC。
⑴在纸上画一个如图所示的钝角三角形,你能折出BC边上
的高吗?与同桌交流你的做法
⑵你能画出此钝角三角形的三条高吗?与同桌交流你的做法
⑶BC边上的高是在三角形的内部还是外部 AB边上的高呢?
⑷钝角三角形的三条高交于一点吗?画一画,试一试它们所
在的直线交于一点吗?将你的结果与同伴进行交流.
研讨四:总结三角形的三条高的特性:
三、巩固训练:
1.如右图,在△ABC中,BC边上的高
是 ,AB边上的高是 ;在
△BCE中,BE边上的高是 ,E C边
上的高是 ;在△ACD中,AC边上的高
是 ,CD边上的高是 ,
2、若一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在 ( )
A. 三角形的内部 B.三角形的外部 C.三角形的一条边上 D. 不能确定
4、下列各组图形中,哪一组图形中AD是△ABC 的高( )
四、延伸迁移:
1.一个缺角三角形残片如图所示,不恢复这个缺角,请你作出AB边上的高所在
的直线.你是怎样作的 为什么
2. 在△ABC中, ∠ACB=90°,AC=3,BC=4,AB=5,CD是AB边上的高,则CD=
五、达标检测:
1、画出上图中△ABC 的三条高。
2、如图所示:(1)在△ABC中,BC边上的高是 ;
(2)在△AEC中,AE边上的高是
(3)在△FEC中,EC边上的高是 ;
3、 如果一个三角形的三条高的交点在三角形的外部,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
4.三角形的三条高所在的直线交于一点,这个交点的位置在( )
A.三角形内B.三角形外C.三边的交点D.根据三角形的形状确定
5.能把三角形的面积平分的是三角形的( )
A.中线 B.高 C.角平分线 D. 一边的垂直平分线
6.如右图在△ABC中,BE平分∠ABC,AD是高,若∠BAD=45°,则∠BED=
8.如右图在△ABC中, ∠B=34°, ∠ACB=104°,AD是BC边上的高,AE
是∠BAC的角平分线,求∠DAE的度数是
9.如图,在△ABC中 ,AD平分∠BAC,AE⊥BC于E, ∠B=36°, ∠C=48°,
求∠DAE的度数。
板书设计:三角形的角平分线和中线
一:概念
二:重点研讨:
研讨一:三角形角平分线的特点和几何表达式
研讨二:三角形中线的特点和几何表达式
三:巩固练习
四:延伸迁移
教学反思:学生对于角平分线和中线比较好接受 ( http: / / www.21cnjy.com ),但是对于一些需要掌握规律和技巧的题目不会灵活运用,(表现在会用公式,但是一遇到新的题目,就不会使用了)因此需要多加练习。
板书设计:三角形的高
一:概念
二:重点研讨:
研讨一:锐角三角形高的特点
研讨二:直角三角形高的特点
研讨三:钝角三角形高的特点
研讨四:总结三角形三条高的特征
三:巩固练习
四:延伸迁移
教学反思:学生对于锐角三角形的三条高比较熟 ( http: / / www.21cnjy.com )悉,但是对于直角三角形和钝角三角形往往容易搞混,特别是对于钝角三角形不能很正确的判定三条高以及正确画出钝角三角形的三条高,可以通过让学生相互讨论和交流,总结出自己的一套方法。
A
C
B
D
A
D
C
B
B
D
C
A
A
C
B
D
A
D
E
I
C
B
A
C
B
A
B
C
A
B
C
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
A
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
A
B
C
B
A
学习目标:1、通过折纸、画图等活动,认识三角形的中线、角平分线,会用几何语言表示。
2、会画出任意三角形的中线、角平分线,通过画图了解各种三角形三条中线、角平分线的位置关系。
学习重点:会画出任意三角形的中线、角平分线,通过画图了解各种三角形三条中线、角平分线的位置关系。
自主探究:(预习课本143—144页,完成下列各题)
1、在三角形中,_______________________________,这个角的顶点与交点之间的________叫三角形的角平分线。
2、在三角形中, _______________________________,叫做这个三角形的中线.
二、重点研讨:
研讨一:请你画出锐角三角形、直角三角形、钝角三角形的所有角平分线,并且观察这些角平分线有什么规律?
一个三角形共有_______条角平分线,他们都在三角形____部,而且相交于 点。
如图:∵AD是三角形ABC的角平分线。
∴ =_______=∠BAC
或∠BAC=_______=
例题:△ABC中,∠B=800 ,∠C=400,BO、CO平分∠B、∠C,则∠BOC=________。
研讨二:请你画出锐角三角形、直角三角形、钝角三角形的所有中线,并且观察这些中线有什么规律?
一个三角形共有_______条中线,他们都在三角形____部,而且相交于 点。
如图:∵AD是三角形ABC的角平分线。
∴BD=______=_______
或:_____=2BD=_______
三、巩固训练: 1、如图所示, BE、CD是角
平分线,∠A=80°,则∠1+∠2=________
2、如图,已知AD是BC边上的中线,AB=5cm,AD=4cm,△ABD的周长是12cm,求BC的长。
3、如图,在△ABC中,∠BAC=600, ∠B=450,AD是△ABC的一条角平分线,
求∠ADB的度数。
.
4、如图所示,AD是△ABC的边BC上的中线,若△ABD的周长比△ACD的周长
大5,求AB与AC的差.
四、延伸迁移:
1、如图,在ΔABC中,角平分线BD,CE相交与I,则∠BIC与∠A有什么关系 如果设∠A为α,求∠BIC(用α表示).利用上述关系,计算:
(1)当∠A=50°时,求∠BIC;
(2)当∠BIC=130°时,求∠A.
2、等腰三角形一腰上的中线把该三角形的周长分别为13.5cm和11.5cm两部分。求这个等腰三角形各边长。
五、达标检测:
1、三角形的中线是( )
A、直线 B、 射线 C、 线段 D、以上答案都不对
2、已知△ABC中,∠B=∠C=50°,AD为∠BAC的平分线,则∠BAD=( )
A 40° B 45° C 50° D 55
3、已知AD是△ABC的中线,且AB=8cm. AC=5cm,则△ABD与△ACD的周长之差为 ,
4、直角三角形两锐角平分线相交所成的角的度数是
5、在△ABC中,AD是BC边上的中线,△ABC的周长比△ACD的周长多5cm,AB与AC的和为11cm,求AB的长。
5.1认识三角形(4)
学习目标:1、通过折纸、画图等活动,认识三角形的高。
2、会画出任意三角形的高(尤其是钝角三角形),通过画图了解各种三角形三条高的位置关系。
学习重点:会画出任意三角形的高,通过画图了解各种三角形三条高的位置关系。
自主探究:(预习课本145页“做一做”上面的内容)
从三角形的一个顶点向它的对边所在直线作垂线, 叫做三角形的高线,简称 。
二、重点研讨:
研讨一:如图,一个锐角△ABC,
⑴ 你能画出这个三角形的三条高吗
⑵ 每人准备一个锐角三角形纸片,你能用折纸的办法
得到它们吗 与同桌交流你的做法
⑶ 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.
研讨二:如图,一个直角△ABC。
⑴画出直角三角形的三条高,
直角边BC边上的高是 ;
直角边AB边上的高是 ;
它们有怎样的位置关系?将你的结果与同伴进行交流.
研讨三:如图,一个钝角三角形△ABC。
⑴在纸上画一个如图所示的钝角三角形,你能折出BC边上
的高吗?与同桌交流你的做法
⑵你能画出此钝角三角形的三条高吗?与同桌交流你的做法
⑶BC边上的高是在三角形的内部还是外部 AB边上的高呢?
⑷钝角三角形的三条高交于一点吗?画一画,试一试它们所
在的直线交于一点吗?将你的结果与同伴进行交流.
研讨四:总结三角形的三条高的特性:
三、巩固训练:
1.如右图,在△ABC中,BC边上的高
是 ,AB边上的高是 ;在
△BCE中,BE边上的高是 ,E C边
上的高是 ;在△ACD中,AC边上的高
是 ,CD边上的高是 ,
2、若一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在 ( )
A. 三角形的内部 B.三角形的外部 C.三角形的一条边上 D. 不能确定
4、下列各组图形中,哪一组图形中AD是△ABC 的高( )
四、延伸迁移:
1.一个缺角三角形残片如图所示,不恢复这个缺角,请你作出AB边上的高所在
的直线.你是怎样作的 为什么
2. 在△ABC中, ∠ACB=90°,AC=3,BC=4,AB=5,CD是AB边上的高,则CD=
五、达标检测:
1、画出上图中△ABC 的三条高。
2、如图所示:(1)在△ABC中,BC边上的高是 ;
(2)在△AEC中,AE边上的高是
(3)在△FEC中,EC边上的高是 ;
3、 如果一个三角形的三条高的交点在三角形的外部,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
4.三角形的三条高所在的直线交于一点,这个交点的位置在( )
A.三角形内B.三角形外C.三边的交点D.根据三角形的形状确定
5.能把三角形的面积平分的是三角形的( )
A.中线 B.高 C.角平分线 D. 一边的垂直平分线
6.如右图在△ABC中,BE平分∠ABC,AD是高,若∠BAD=45°,则∠BED=
8.如右图在△ABC中, ∠B=34°, ∠ACB=104°,AD是BC边上的高,AE
是∠BAC的角平分线,求∠DAE的度数是
9.如图,在△ABC中 ,AD平分∠BAC,AE⊥BC于E, ∠B=36°, ∠C=48°,
求∠DAE的度数。
板书设计:三角形的角平分线和中线
一:概念
二:重点研讨:
研讨一:三角形角平分线的特点和几何表达式
研讨二:三角形中线的特点和几何表达式
三:巩固练习
四:延伸迁移
教学反思:学生对于角平分线和中线比较好接受 ( http: / / www.21cnjy.com ),但是对于一些需要掌握规律和技巧的题目不会灵活运用,(表现在会用公式,但是一遇到新的题目,就不会使用了)因此需要多加练习。
板书设计:三角形的高
一:概念
二:重点研讨:
研讨一:锐角三角形高的特点
研讨二:直角三角形高的特点
研讨三:钝角三角形高的特点
研讨四:总结三角形三条高的特征
三:巩固练习
四:延伸迁移
教学反思:学生对于锐角三角形的三条高比较熟 ( http: / / www.21cnjy.com )悉,但是对于直角三角形和钝角三角形往往容易搞混,特别是对于钝角三角形不能很正确的判定三条高以及正确画出钝角三角形的三条高,可以通过让学生相互讨论和交流,总结出自己的一套方法。
A
C
B
D
A
D
C
B
B
D
C
A
A
C
B
D
A
D
E
I
C
B
A
C
B
A
B
C
A
B
C
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
A
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
A
B
C
B
A
