七年级数学下册11.6 一元一次不等式组 学案 鲁教版五四制
文档属性
| 名称 | 七年级数学下册11.6 一元一次不等式组 学案 鲁教版五四制 |  | |
| 格式 | zip | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-18 17:32:34 | ||
图片预览


文档简介
一元一次不等式组
展示课(时段: 正课 时间:45 分钟 )
学习目标:1、理解一元一次不等式组及其解集的定义
2、会借助数轴求一元一次不等式组的解集.
学习重难点:借助数轴求一元一次不等式组的解集
【定向导学·互动展示·当堂反馈】
课 堂 元 素 自学(自研自探) 合学(合作探究) 展学(展示质疑)
学 法 指 导( 内容·学法·时间 ) 互 动 策 略 (内容·形式·时间) 展 示 方 案(内容·方式·时间)
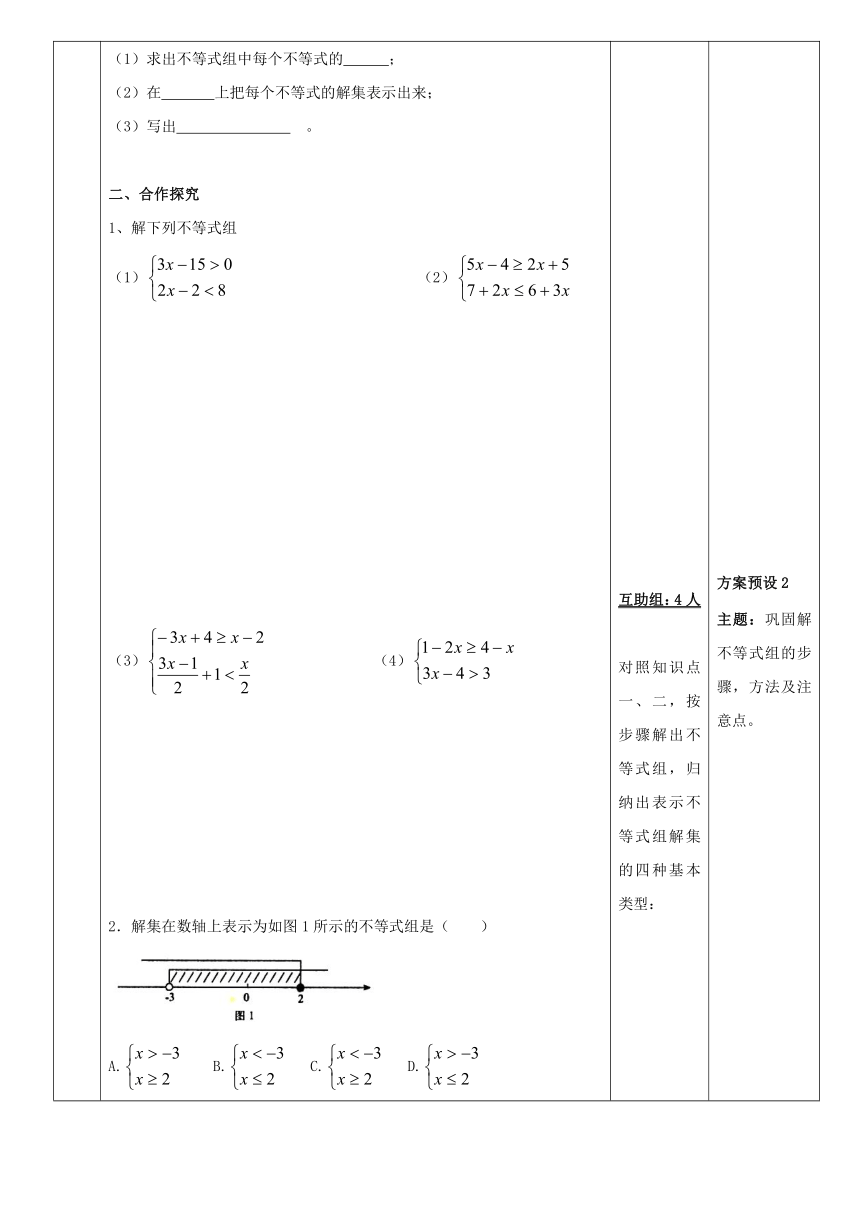
概念认知·例题导析 自研自探:知识点一 类比方程组的概念理解一元一次不等式组的相关概念 1、几个 合在一起,就组成了一个一元一次不等式组,这些不等式必须含同一个未知数.2、一元一次不等式组的解集是指一元一次不等式组里所有一元一次不等式的解集的 部分.知识点二 一元一次不等式组的解法及步骤 一元一次不等式组的解法: 解不等式①得:解不等式②得:把不等式①和不等式②的解集在数轴上表示出来从上图可以找出两个不等式解集的公共部分,得不等式组的解集为一元一次不等式组的步骤:(1)求出不等式组中每个不等式的 ;(2)在 上把每个不等式的解集表示出来;(3)写出 。二、合作探究1、解下列不等式组(1) (2)(3) ( http: / / www.21cnjy.com ) (4) 2.解集在数轴上表示为如图1所示的不等式组是( )A. B. C. D. 两人小对子在独学的基础上,根据批改情况,对子间互查互检,主要查概念,查步骤,查方法,查注意点。互助组:4人对照知识点一、二,按步骤解出不等式组,归纳出表示不等式组解集的四种基本类型:共同体:全组分工预展在行政大组长的主持下,根据本组的展示内容做好分工,完成版面设计,做好展示前的预展. 方案预设1主题:揭示本节知识要点,辅助学生完成独.并且渗透类比思想,得出一元一次不等式组以及其解集的概念,利用数轴的直观理解不等式解集的意义.方案预设2主题:巩固解不等式组的步骤,方法及注意点。方案预设3主题: 根据不等式组解集在数轴上的表示,逆向表示符合要求的不等式组
应用探究 若不等式组的解集为,则的大小关系是
梳理小结 四、【梳理小结】由两个一元一次不等式组成的不等式组的解集,可归纳为以下四种基本类型:设<①的解集为 ; ②的解集为 ;③的解集为 ; ④的解集为 .口诀为:同大取 ,同小取 ,大小小大两边夹,大大小小无解答
查学 1.把不等式组的解集表示在数轴上,正确的是( )(3分)2.若不等式组的解集为,则的大小关系是 (3分)3、不等式组 ( http: / / www.21cnjy.com )的整数解是 .(4分)
9、3 一元一次不等式组(1) 评学(训练课) 日清三层级能力提升达标题 自评: 师评:
基础题:
选择题(每题4分,共16分)
1.不等式组 的解集是 ( )
x ≤ 5 B.- 3 < x≤ 5 C. 3 < x≤ 5 D.x < -3
2.不等式组的解集在数轴上可表示为( )
A、 B、
C、 D、
在平面直角坐标系中,若点P(m - 3 ,m+1)在第二象限,则m的取值范围是 ( )
-1 < m < 3 B.m > 3 C.m < - 1 D.m > -1
不等式组的解集是 x > 2 ,则m的取值范围是 ( )
m ≤ 2 B.m ≥ 2 C.m ≤ 1 D.m > 1
填空题(每题4分,共16分)
不等式组 的解集是
不等式组 的整数解的和是
若不等式组的解集是 -18.若不等式组有解,那么a 必须满足 (提高题)
解答题
解不等式组,并把解集在数轴上表示出来
(1) (2) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) (4) ( http: / / www.21cnjy.com )
某商店需要购进甲、乙两种商品共160件,其进价的售价如下表(注:获利= 售价 - 进价)
甲 乙
进价(元/ 件) 15 35
售价(元/ 件) 20 45
若商店计划销售完这批商品后,能获得1100元,问甲、乙两种商品应分别购进多少件?
若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
培辅课:
你需要培辅吗?(需要,不需要)
2、效果描述
学生签字:
反思课(师\生):
收获:
疑惑:
展示课(时段: 正课 时间:45 分钟 )
学习目标:1、理解一元一次不等式组及其解集的定义
2、会借助数轴求一元一次不等式组的解集.
学习重难点:借助数轴求一元一次不等式组的解集
【定向导学·互动展示·当堂反馈】
课 堂 元 素 自学(自研自探) 合学(合作探究) 展学(展示质疑)
学 法 指 导( 内容·学法·时间 ) 互 动 策 略 (内容·形式·时间) 展 示 方 案(内容·方式·时间)
概念认知·例题导析 自研自探:知识点一 类比方程组的概念理解一元一次不等式组的相关概念 1、几个 合在一起,就组成了一个一元一次不等式组,这些不等式必须含同一个未知数.2、一元一次不等式组的解集是指一元一次不等式组里所有一元一次不等式的解集的 部分.知识点二 一元一次不等式组的解法及步骤 一元一次不等式组的解法: 解不等式①得:解不等式②得:把不等式①和不等式②的解集在数轴上表示出来从上图可以找出两个不等式解集的公共部分,得不等式组的解集为一元一次不等式组的步骤:(1)求出不等式组中每个不等式的 ;(2)在 上把每个不等式的解集表示出来;(3)写出 。二、合作探究1、解下列不等式组(1) (2)(3) ( http: / / www.21cnjy.com ) (4) 2.解集在数轴上表示为如图1所示的不等式组是( )A. B. C. D. 两人小对子在独学的基础上,根据批改情况,对子间互查互检,主要查概念,查步骤,查方法,查注意点。互助组:4人对照知识点一、二,按步骤解出不等式组,归纳出表示不等式组解集的四种基本类型:共同体:全组分工预展在行政大组长的主持下,根据本组的展示内容做好分工,完成版面设计,做好展示前的预展. 方案预设1主题:揭示本节知识要点,辅助学生完成独.并且渗透类比思想,得出一元一次不等式组以及其解集的概念,利用数轴的直观理解不等式解集的意义.方案预设2主题:巩固解不等式组的步骤,方法及注意点。方案预设3主题: 根据不等式组解集在数轴上的表示,逆向表示符合要求的不等式组
应用探究 若不等式组的解集为,则的大小关系是
梳理小结 四、【梳理小结】由两个一元一次不等式组成的不等式组的解集,可归纳为以下四种基本类型:设<①的解集为 ; ②的解集为 ;③的解集为 ; ④的解集为 .口诀为:同大取 ,同小取 ,大小小大两边夹,大大小小无解答
查学 1.把不等式组的解集表示在数轴上,正确的是( )(3分)2.若不等式组的解集为,则的大小关系是 (3分)3、不等式组 ( http: / / www.21cnjy.com )的整数解是 .(4分)
9、3 一元一次不等式组(1) 评学(训练课) 日清三层级能力提升达标题 自评: 师评:
基础题:
选择题(每题4分,共16分)
1.不等式组 的解集是 ( )
x ≤ 5 B.- 3 < x≤ 5 C. 3 < x≤ 5 D.x < -3
2.不等式组的解集在数轴上可表示为( )
A、 B、
C、 D、
在平面直角坐标系中,若点P(m - 3 ,m+1)在第二象限,则m的取值范围是 ( )
-1 < m < 3 B.m > 3 C.m < - 1 D.m > -1
不等式组的解集是 x > 2 ,则m的取值范围是 ( )
m ≤ 2 B.m ≥ 2 C.m ≤ 1 D.m > 1
填空题(每题4分,共16分)
不等式组 的解集是
不等式组 的整数解的和是
若不等式组的解集是 -1
解答题
解不等式组,并把解集在数轴上表示出来
(1) (2) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) (4) ( http: / / www.21cnjy.com )
某商店需要购进甲、乙两种商品共160件,其进价的售价如下表(注:获利= 售价 - 进价)
甲 乙
进价(元/ 件) 15 35
售价(元/ 件) 20 45
若商店计划销售完这批商品后,能获得1100元,问甲、乙两种商品应分别购进多少件?
若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
培辅课:
你需要培辅吗?(需要,不需要)
2、效果描述
学生签字:
反思课(师\生):
收获:
疑惑:
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
