一次函数的运用
图片预览

文档简介
第14课时 一次函数及其应用(一)
一、教学目标:
【知识与技能】了解并掌握,一次函数中的基础知识,体会数形结合的优越性,培养学生的观察意识和能力。
【过程与方法】培养学生学习数学的主动性,提高数学表达能力,发展分析和解决问题的能力。
【情感、态度与价值观】激发学生的求知欲,培养学生积极探索,勇于创新的精神。
二、教学重难点:
一次函数基本性质以及用性质解决实际生活中所涉及的有关问题,体会利用数形结合思想解决问题的优越性。
三、教与学互动设计:
(一)考点整合
1、一次函数与正比例函数的定义
若两变量、间的关系式可以表示成的形式,则称是的一次函数,特别地,当时,即,叫正比例函数。
2、一次函数的图象及性质
①一次函数的图象是一条直线,一次函数的图象也称为直线,画一次函数的图象的方法,只要确定两个点(0,b),(-,o),再过这两个点作直线即可。
特别的正比例函数的图象是经过两点O(0,0),的一条直线。
②时,随增大而 增大 ,并且时,函数图象在第 一、二、三 象限;
时,函数图象在第 一、三 象限;且过原点。
时,函数图象在第 一、三、四 象限;
时,随增大而 减小 ,并且时,函数图象在第 一、二、四 象限;
时,函数图象在第 二、四 象限;且过原点。
时,函数图象在第 二、三、四 象限;
3、求一次函数解析式:
用待定系数法 求一次函数解析式。
步骤(1)设出一般式。
(2)由已知条件代入解析式,得到关于、二元一次方程组。
(3)求出方程组中的、值。
(4)将、值返代回中,即为所求。
(二)应用示例
A.基础应用
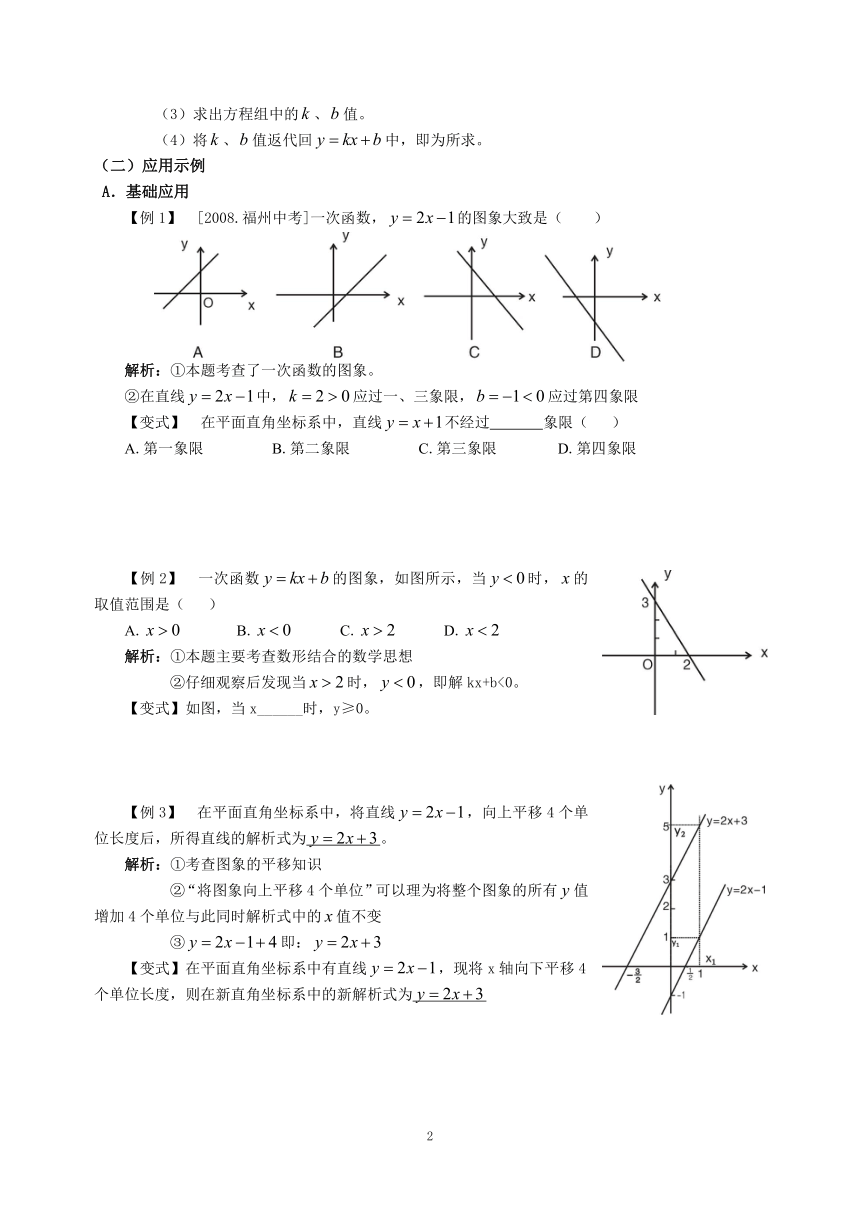
【例1】 [2008.福州中考]一次函数,的图象大致是( )
解析:①本题考查了一次函数的图象。
②在直线中,应过一、三象限,应过第四象限
【变式】 在平面直角坐标系中,直线不经过 象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【例2】 一次函数的图象,如图所示,当时,的取值范围是( )
A. B. C. D.
解析:①本题主要考查数形结合的数学思想
②仔细观察后发现当时,,即解kx+b<0。
【变式】如图,当x______时,y≥0。
【例3】 在平面直角坐标系中,将直线,向上平移4个单位长度后,所得直线的解析式为。
解析:①考查图象的平移知识
②“将图象向上平移4个单位”可以理为将整个图象的所有值增加4个单位与此同时解析式中的值不变
③即:
【变式】在平面直角坐标系中有直线,现将x轴向下平移4个单位长度,则在新直角坐标系中的新解析式为
【例4】 已知一条直线经过A(30,400),(50,0)两点,求该直线解析式。
解:设与之间的关系式为:
由题意得:
【例5】 [2008.宜昌]为积极响应党中央关于支援5.12汶川地震灾区抗震救灾的号召,某加工厂日夜连续加班,计划为灾区生产顶帐篷,生产过程中的剩余生产任务(项)与已用生产时间(时)之间的关系如图所示。
求:变量与之间的关系式。
解析:由于图象是不平行于坐标轴的线段(即直线的一部分),所以设与之间的关系式为,利用“待定系数法”求出、的值,从而达到解决问题的目的。
解:设与之间的关系式为:
由题意得:
B.升华应用
【例6】 在购买某场足球赛门票时,设购买门票数为(张),总费用为(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)。
方案二:购买门票方式如图所示。
解答下列问题:
(1)方案一中,与的函数关系式为;
方案二中,当时,与的函数关系式为;
当时,与的函数关系式为;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张。
解:(2)方案一中与的函数关系式为
>100,方案二的与的函关系式为
当时,即时,选方案二进行购买。
当时,即时,两种方案都可以。
当时,即时,选方案一进行购买。
(3)设甲、乙单位购买本次足球赛门票数分别为张和张。
甲、乙单位分别采用方案一和方案二购买本次足球比赛门票。
乙公司购买本次足球赛门票有两种情况:或
①当时,乙公司购买本次足球赛门票费用为
不符合题意应舍去
②当时,乙公司购买本次足球赛门票费为
符合题意
答:甲、乙单位购买本次足球赛门票分别为500张、200张。
四、课后小结:
本节课,我们复习了一次函数这章节中的概念、图象、性质及其简单的应用,加深了同学们对相关知识的理解,进一步渗透了数形结合的数学思想。
五、课后作业:《全品》P40,1—8小题
k<0,b<0
k>0,b=0
k>0,b<0
k>0,b>0
k<0,b>0
k<0,b=0
(1) (2) (3) (4) (5) (6)
PAGE
4
一、教学目标:
【知识与技能】了解并掌握,一次函数中的基础知识,体会数形结合的优越性,培养学生的观察意识和能力。
【过程与方法】培养学生学习数学的主动性,提高数学表达能力,发展分析和解决问题的能力。
【情感、态度与价值观】激发学生的求知欲,培养学生积极探索,勇于创新的精神。
二、教学重难点:
一次函数基本性质以及用性质解决实际生活中所涉及的有关问题,体会利用数形结合思想解决问题的优越性。
三、教与学互动设计:
(一)考点整合
1、一次函数与正比例函数的定义
若两变量、间的关系式可以表示成的形式,则称是的一次函数,特别地,当时,即,叫正比例函数。
2、一次函数的图象及性质
①一次函数的图象是一条直线,一次函数的图象也称为直线,画一次函数的图象的方法,只要确定两个点(0,b),(-,o),再过这两个点作直线即可。
特别的正比例函数的图象是经过两点O(0,0),的一条直线。
②时,随增大而 增大 ,并且时,函数图象在第 一、二、三 象限;
时,函数图象在第 一、三 象限;且过原点。
时,函数图象在第 一、三、四 象限;
时,随增大而 减小 ,并且时,函数图象在第 一、二、四 象限;
时,函数图象在第 二、四 象限;且过原点。
时,函数图象在第 二、三、四 象限;
3、求一次函数解析式:
用待定系数法 求一次函数解析式。
步骤(1)设出一般式。
(2)由已知条件代入解析式,得到关于、二元一次方程组。
(3)求出方程组中的、值。
(4)将、值返代回中,即为所求。
(二)应用示例
A.基础应用
【例1】 [2008.福州中考]一次函数,的图象大致是( )
解析:①本题考查了一次函数的图象。
②在直线中,应过一、三象限,应过第四象限
【变式】 在平面直角坐标系中,直线不经过 象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【例2】 一次函数的图象,如图所示,当时,的取值范围是( )
A. B. C. D.
解析:①本题主要考查数形结合的数学思想
②仔细观察后发现当时,,即解kx+b<0。
【变式】如图,当x______时,y≥0。
【例3】 在平面直角坐标系中,将直线,向上平移4个单位长度后,所得直线的解析式为。
解析:①考查图象的平移知识
②“将图象向上平移4个单位”可以理为将整个图象的所有值增加4个单位与此同时解析式中的值不变
③即:
【变式】在平面直角坐标系中有直线,现将x轴向下平移4个单位长度,则在新直角坐标系中的新解析式为
【例4】 已知一条直线经过A(30,400),(50,0)两点,求该直线解析式。
解:设与之间的关系式为:
由题意得:
【例5】 [2008.宜昌]为积极响应党中央关于支援5.12汶川地震灾区抗震救灾的号召,某加工厂日夜连续加班,计划为灾区生产顶帐篷,生产过程中的剩余生产任务(项)与已用生产时间(时)之间的关系如图所示。
求:变量与之间的关系式。
解析:由于图象是不平行于坐标轴的线段(即直线的一部分),所以设与之间的关系式为,利用“待定系数法”求出、的值,从而达到解决问题的目的。
解:设与之间的关系式为:
由题意得:
B.升华应用
【例6】 在购买某场足球赛门票时,设购买门票数为(张),总费用为(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)。
方案二:购买门票方式如图所示。
解答下列问题:
(1)方案一中,与的函数关系式为;
方案二中,当时,与的函数关系式为;
当时,与的函数关系式为;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张。
解:(2)方案一中与的函数关系式为
>100,方案二的与的函关系式为
当时,即时,选方案二进行购买。
当时,即时,两种方案都可以。
当时,即时,选方案一进行购买。
(3)设甲、乙单位购买本次足球赛门票数分别为张和张。
甲、乙单位分别采用方案一和方案二购买本次足球比赛门票。
乙公司购买本次足球赛门票有两种情况:或
①当时,乙公司购买本次足球赛门票费用为
不符合题意应舍去
②当时,乙公司购买本次足球赛门票费为
符合题意
答:甲、乙单位购买本次足球赛门票分别为500张、200张。
四、课后小结:
本节课,我们复习了一次函数这章节中的概念、图象、性质及其简单的应用,加深了同学们对相关知识的理解,进一步渗透了数形结合的数学思想。
五、课后作业:《全品》P40,1—8小题
k<0,b<0
k>0,b=0
k>0,b<0
k>0,b>0
k<0,b>0
k<0,b=0
(1) (2) (3) (4) (5) (6)
PAGE
4
