人教版七年级数学下册第五章 相交线与平行线 章节练习题 (含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线 章节练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 15:55:24 | ||
图片预览


文档简介
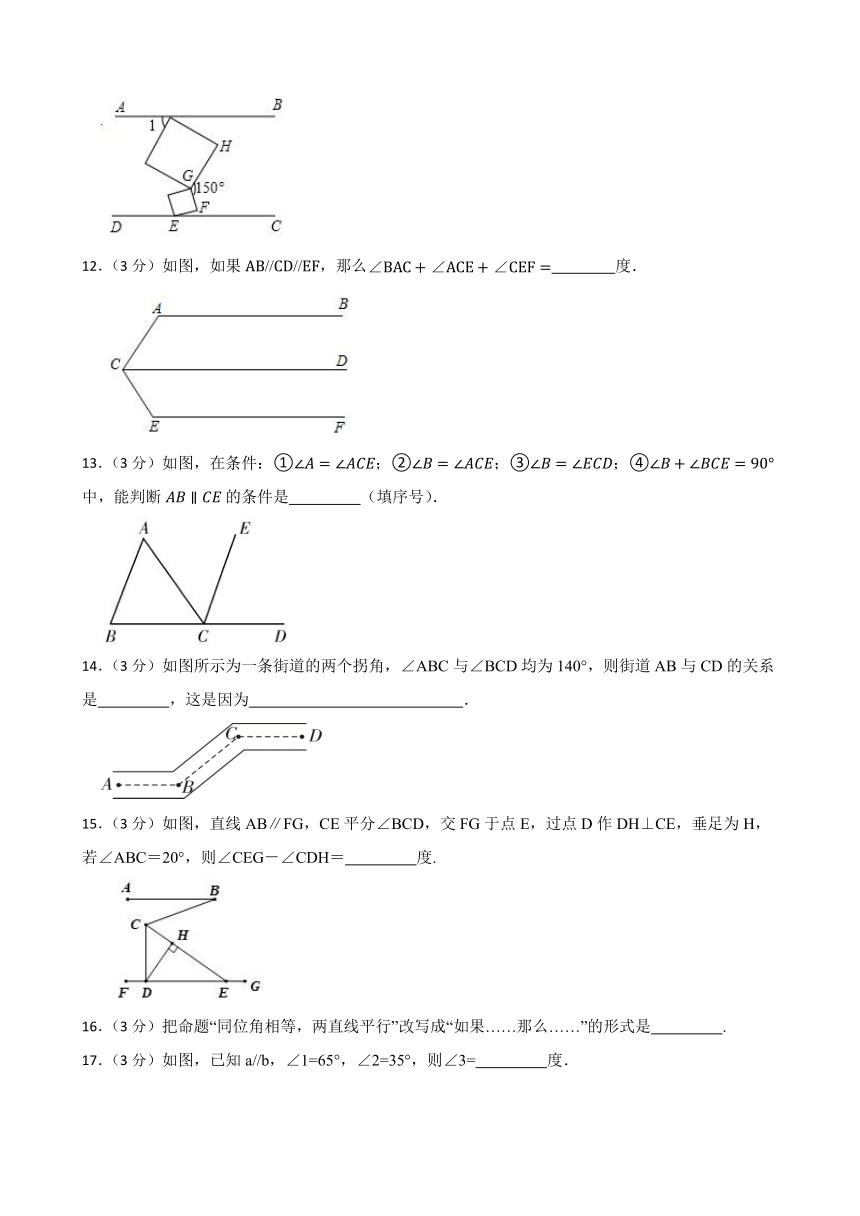
七年级数学下册第五章 相交线与平行线章节练习题
一、选择题(共30分)
1.(3分)下列图形中与是对顶角的是( )
A. B.
C. D.
2.(3分)有下列四个命题:①对顶角相等;②等角的补角相等;③如果b∥a,c∥a,那么b∥c;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.其中是真命题的有( )
A.4个 B.3个 C.2个 D.1个
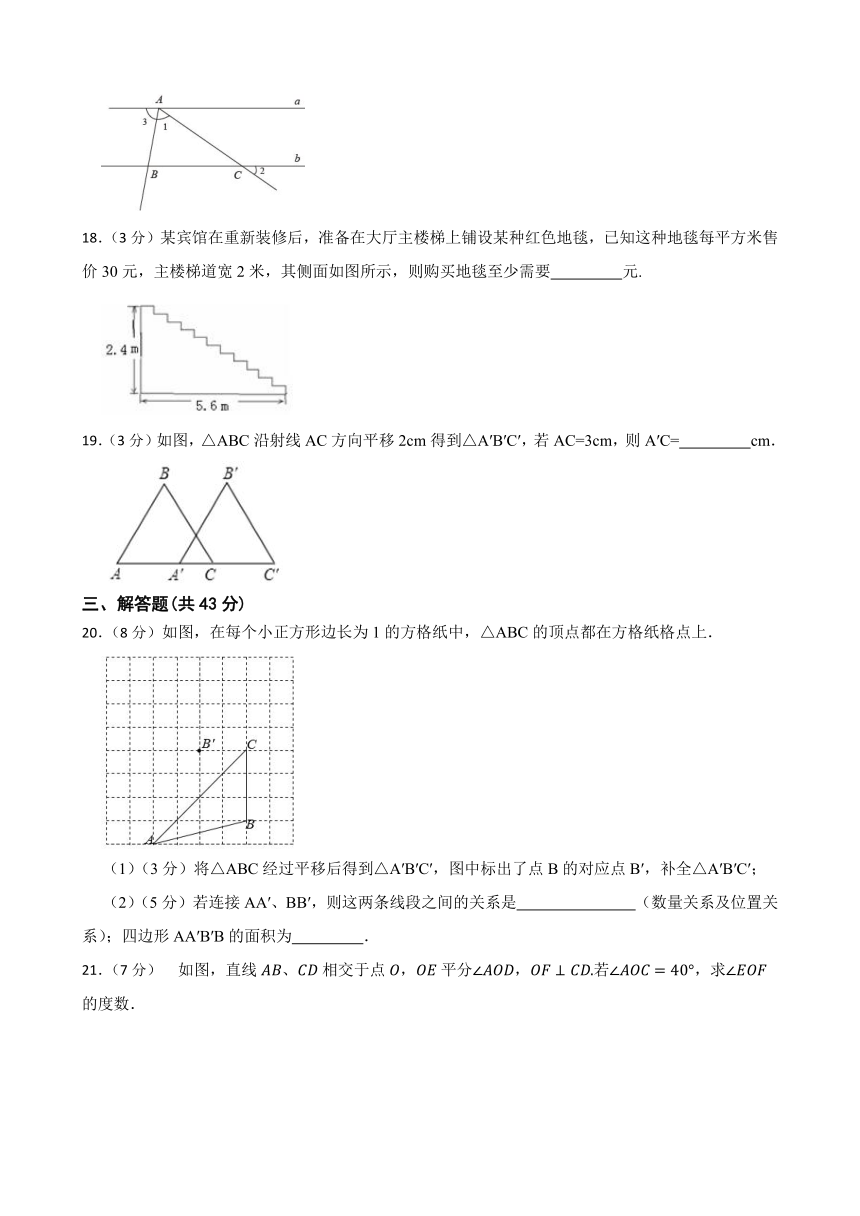
3.(3分)如图,小米同学把一个含45°角的直角三角板放在如图所示的两条平行线m,n上,经测量∠α=115°,则∠β的度数是( )
A.55° B.65° C.75° D.70°
4.(3分)如图,河道的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( )
A.B.C. D.
5.(3分)下列判断错误的是( )
A.与是同旁内角 B.与是内错角
C.与是同旁内角 D.与是同位角
6.(3分)直线a、b、c中,a∥b,b∥c,则直线a与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
7.(3分)如图,能判定EB∥AC的是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠C=∠ABC D.∠BAC=∠ABE
8.(3分)如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
A.140° B.60° C.50° D.40°
9.(3分)如图,直线,直线与直线,分别交于点、,射线直线,则图中与互余的角有( )
A.1个 B.2个 C.3个 D.4个
10.(3分)如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( ).
A.△ABC与△DEF能够重合 B.∠DEF=90°
C.AC=DF D.EC=CF
二、填空题(共27分)
11.(3分)如图,有两个正方形夹在AB与CD中,且AB//CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
12.(3分)如图,如果////,那么 度.
13.(3分)如图,在条件:①;②;③;④中,能判断的条件是 (填序号).
14.(3分)如图所示为一条街道的两个拐角,∠ABC与∠BCD均为140°,则街道AB与CD的关系是 ,这是因为 .
15.(3分)如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH= 度.
16.(3分)把命题“同位角相等,两直线平行”改写成“如果……那么……”的形式是 .
17.(3分)如图,已知a//b,∠1=65°,∠2=35°,则∠3= 度.
18.(3分)某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要 元.
19.(3分)如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C= cm.
三、解答题(共43分)
20.(8分)如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)(3分)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(2)(5分)若连接AA′、BB′,则这两条线段之间的关系是 (数量关系及位置关系);四边形AA′B′B的面积为 .
21.(7分) 如图,直线、相交于点,平分,若,求的度数.
22.(7分)如图,已知BD平分,,.求的度数.
23.(7分)完成推理并填空:如图,点B,E分别在上,,试说明.
解:因为(已知),(对顶角相等),
所以(等量代换),
所以 ▲ ▲ ( )
所以( )
又因为(已知),
所以 ▲ = ▲ (等量代换),
所以 ▲ ▲ (内错角相等,两直线平行),
所以( )
24.(7分)如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,试判断DG与BC的位置关系,并说明理由.
25.(7分)如图,将直角梯形ABCD平移到直角梯形EFGH,若HG=10,MC=2,MG=5,求图中阴影部分面积.
答案解析部分
1.B
2.B
3.D
4.B
5.C
6.B
7.D
8.D
9.D
10.D
11.70
12.AB;CD
13.①③
14.平行;内错角相等,两直线平行
15.110
16.如果两条直线被第三条直线所截且同位角相等,那么这两条直线平行
17.80
18.480.
19.1
20.(1)解:如图:△A′B′C′为所求;
(2)平行且相等;14
21.解:,
,
平分,
,
,
,
.
22.解:∵,
∴,;
∵,
∴.
∵BD平分,
∴;
∴.
23.解:因为(已知),(对顶角相等),
所以(等量代换),
所以(同位角相等,两直线平行)
所以(两直线平行,同位角相等)
又因为(已知),
所以(等量代换),
所以(内错角相等,两直线平行),
所以(两直线平行,内错角相等).
故答案为:BD,CE,同位角相等,两直线平行;两直线平行,同位角相等;∠ABD,∠D;AC,DF;两直线平行,内错角相等.
24.解:DG∥BC,理由如下:
∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠1=∠2,
∴∠1=∠DCE,
∴DG∥BC
25.解:∵阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积,
等于梯形EFGH的面积减去梯形EFMD的面积,
∴阴影部分的面积等于梯形DHGM的面积,
∵HG=10,MC=2,MG=5,
∴S阴=SDHGM=×(8+10)×5=45.
一、选择题(共30分)
1.(3分)下列图形中与是对顶角的是( )
A. B.
C. D.
2.(3分)有下列四个命题:①对顶角相等;②等角的补角相等;③如果b∥a,c∥a,那么b∥c;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.其中是真命题的有( )
A.4个 B.3个 C.2个 D.1个
3.(3分)如图,小米同学把一个含45°角的直角三角板放在如图所示的两条平行线m,n上,经测量∠α=115°,则∠β的度数是( )
A.55° B.65° C.75° D.70°
4.(3分)如图,河道的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( )
A.B.C. D.
5.(3分)下列判断错误的是( )
A.与是同旁内角 B.与是内错角
C.与是同旁内角 D.与是同位角
6.(3分)直线a、b、c中,a∥b,b∥c,则直线a与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
7.(3分)如图,能判定EB∥AC的是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠C=∠ABC D.∠BAC=∠ABE
8.(3分)如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
A.140° B.60° C.50° D.40°
9.(3分)如图,直线,直线与直线,分别交于点、,射线直线,则图中与互余的角有( )
A.1个 B.2个 C.3个 D.4个
10.(3分)如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( ).
A.△ABC与△DEF能够重合 B.∠DEF=90°
C.AC=DF D.EC=CF
二、填空题(共27分)
11.(3分)如图,有两个正方形夹在AB与CD中,且AB//CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
12.(3分)如图,如果////,那么 度.
13.(3分)如图,在条件:①;②;③;④中,能判断的条件是 (填序号).
14.(3分)如图所示为一条街道的两个拐角,∠ABC与∠BCD均为140°,则街道AB与CD的关系是 ,这是因为 .
15.(3分)如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH= 度.
16.(3分)把命题“同位角相等,两直线平行”改写成“如果……那么……”的形式是 .
17.(3分)如图,已知a//b,∠1=65°,∠2=35°,则∠3= 度.
18.(3分)某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要 元.
19.(3分)如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C= cm.
三、解答题(共43分)
20.(8分)如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)(3分)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(2)(5分)若连接AA′、BB′,则这两条线段之间的关系是 (数量关系及位置关系);四边形AA′B′B的面积为 .
21.(7分) 如图,直线、相交于点,平分,若,求的度数.
22.(7分)如图,已知BD平分,,.求的度数.
23.(7分)完成推理并填空:如图,点B,E分别在上,,试说明.
解:因为(已知),(对顶角相等),
所以(等量代换),
所以 ▲ ▲ ( )
所以( )
又因为(已知),
所以 ▲ = ▲ (等量代换),
所以 ▲ ▲ (内错角相等,两直线平行),
所以( )
24.(7分)如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,试判断DG与BC的位置关系,并说明理由.
25.(7分)如图,将直角梯形ABCD平移到直角梯形EFGH,若HG=10,MC=2,MG=5,求图中阴影部分面积.
答案解析部分
1.B
2.B
3.D
4.B
5.C
6.B
7.D
8.D
9.D
10.D
11.70
12.AB;CD
13.①③
14.平行;内错角相等,两直线平行
15.110
16.如果两条直线被第三条直线所截且同位角相等,那么这两条直线平行
17.80
18.480.
19.1
20.(1)解:如图:△A′B′C′为所求;
(2)平行且相等;14
21.解:,
,
平分,
,
,
,
.
22.解:∵,
∴,;
∵,
∴.
∵BD平分,
∴;
∴.
23.解:因为(已知),(对顶角相等),
所以(等量代换),
所以(同位角相等,两直线平行)
所以(两直线平行,同位角相等)
又因为(已知),
所以(等量代换),
所以(内错角相等,两直线平行),
所以(两直线平行,内错角相等).
故答案为:BD,CE,同位角相等,两直线平行;两直线平行,同位角相等;∠ABD,∠D;AC,DF;两直线平行,内错角相等.
24.解:DG∥BC,理由如下:
∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠1=∠2,
∴∠1=∠DCE,
∴DG∥BC
25.解:∵阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积,
等于梯形EFGH的面积减去梯形EFMD的面积,
∴阴影部分的面积等于梯形DHGM的面积,
∵HG=10,MC=2,MG=5,
∴S阴=SDHGM=×(8+10)×5=45.
