人教版七年级数学下册第五章 相交线与平行线 章节练习题(含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线 章节练习题(含答案) | 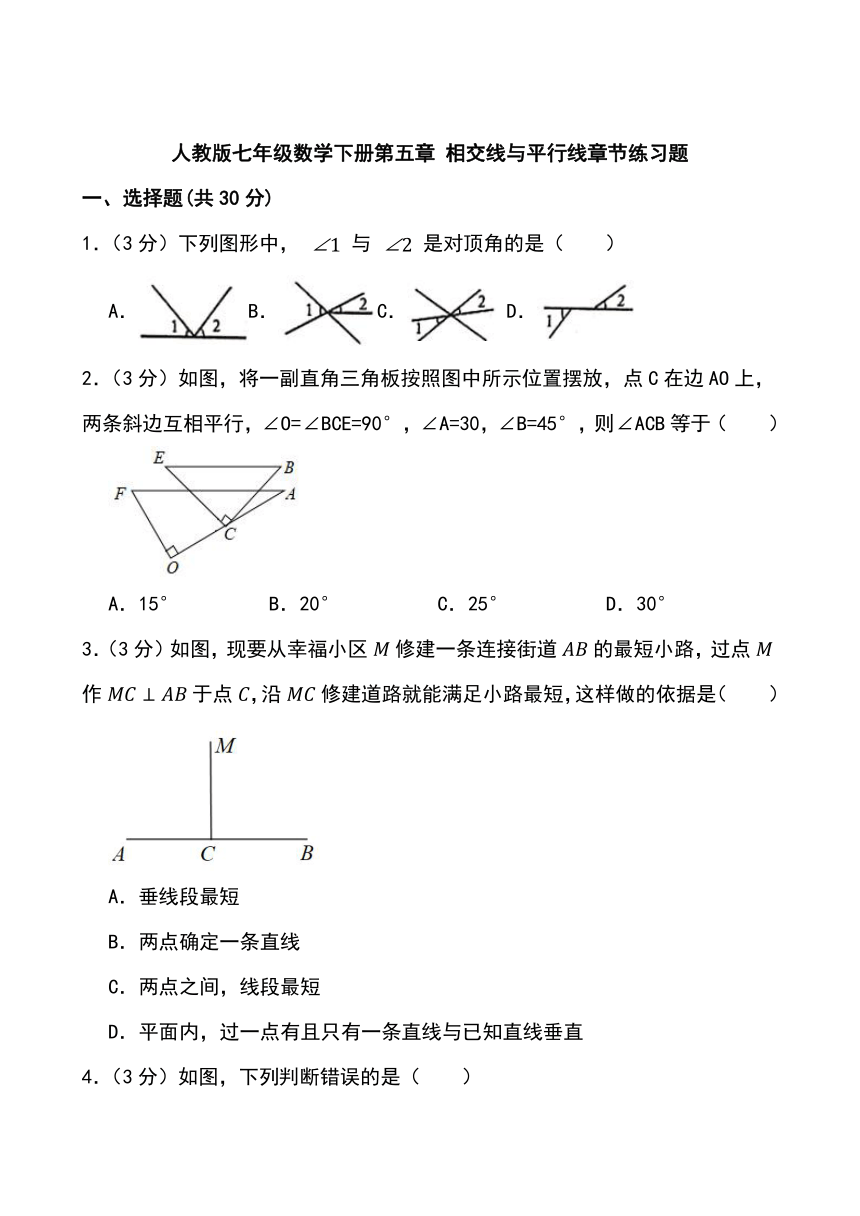 | |
| 格式 | docx | ||
| 文件大小 | 257.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 15:56:50 | ||
图片预览


文档简介
人教版七年级数学下册第五章 相交线与平行线章节练习题
一、选择题(共30分)
1.(3分)下列图形中, 与 是对顶角的是( )
A.B.C. D.
2.(3分)如图,将一副直角三角板按照图中所示位置摆放,点C在边AO上,两条斜边互相平行,∠O=∠BCE=90°,∠A=30,∠B=45°,则∠ACB等于( )
A.15° B.20° C.25° D.30°
3.(3分)如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点,沿修建道路就能满足小路最短,这样做的依据是( )
A.垂线段最短
B.两点确定一条直线
C.两点之间,线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
4.(3分)如图,下列判断错误的是( )
A.∠1和∠2是同旁内角 B.∠3和∠4是内错角
C.∠5和∠6是同旁内角 D.∠5和∠8是同位角
5.(3分)若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不对
6.(3分)如图,已知∠B=∠AEF,则( )
A.EF∥BC B.AD∥EF C.AD∥BC D.AB∥CD
7.(3分)一把直尺和一块含30°角的直角三角板ABC按如图方式摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )
A.5° B.15° C.25° D.35°
8.(3分)有下列四个命题:①对顶角相等;②等角的补角相等;③如果b∥a,c∥a,那么b∥c;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.其中是真命题的有( )
A.4个 B.3个 C.2个 D.1个
9.(3分)如图的图案是由下列四个选项中的哪个图案平移得到的( )
A. B. C. D.
10.(3分)如图,将△ABC沿着水平方向向右平移后得到△DEF,若BC=5,CE=3,则平移的距离为( )
A.1 B.2 C.3 D.5
二、填空题(共27分)
11.(3分)如图,如果////,那么 度.
12.(3分)一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有 .(填序号)
13.(3分)如图,将木条a,b与钉在一起,,,要使木条与平行,木条转动的度数至少是 度.
14.(3分)如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是 。
15.(3分)如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若,则的度数为 .
16.(3分)把命题“平行于同一条直线的两条直线互相平行”改写成“如果…,那么…”的形式为
17.(3分)如图,已知CD平分∠ACB,DE∥AC,∠ACD=30°,则∠DEB=
18.(3分)如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为 .
19.(3分)如图:直角△ABC中,AC=3,BC=4,AB=5,则内部五个小直角三角形的周长为 .
三、解答题(共43分)
20.(8分)在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)(4分)请你作出平移后的图形△DEF;
(2)(4分)请求出△DEF的面积(每个网格是边长为1的正方形).
21.(7分)如图,射线 的端点O在直线 上, 于点O,且 平分 , 平分 ,若 ,分别求 与 的度数.
22.(7分)已知,如图,EF∥MN,且∠1=∠2,∠3=∠4,求证:AB∥CD.
23.(7分)请把下面的说理过程补充完整:
已知:如图,CD平分∠ACB,,那么EF平分∠DEB吗?请说明理由.
解:EF平分∠DEB.理由如下:
∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵(已知),
∴∠DCA= ▲ ,
∴∠DCE=∠CDE(等量代换),
∵(已知),
∴ ▲ =∠CDE( ),∠DCE=∠BEF( ),
∴ ▲ = ▲ (等量代换),
∴EF平分∠DEB( )
24.(7分)如图, , ,垂足分别为 ,且 ,求证: .
25.(7分)如图,将直角三角形ABC沿着BC方向平移到三角形DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.
答案解析部分
1.C
2.A
3.A
4.C
5.B
6.A
7.C
8.A
9.B
10.B
11.360
12.①④
13.25
14.同位角相等,两直线平行
15.
16.如果两条直线平行于同一条直线,那么这两条直线平行
17.60°
18.1200
19.12
20.(1) 如图所示,△DEF就是所求的三角形,
(2)解:△DEF的面积 =3×4-=4
21.解:∵ ,
∴∠COE=90 ,
∵ ,
∴∠BOE=20 ,
∵ 平分 ,
∴∠DOE=∠BOE=20 ,
∴∠AOE=160 ,
∵ 平分 ,
∴∠EOF=80 ,
∴∠DOF=∠EOF-∠DOE=60 .
22.解:∵EF∥MN,
∴∠2=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠BAC=180°﹣(∠1+∠2),∠DCA=180°﹣(∠3+∠4),
∴∠BAC=∠DCA,
∴AB∥CD
23.解:EF平分∠DEB.理由如下:
∵CD平分∠ACB(已知),∴∠DCA=∠DCE(角平分线的定义),
∵(已知),∴∠DCA=∠CDE,∴∠DCE=∠CDE(等量代换),
∵(已知),∴∠DEF=∠CDE(两直线平行,内错角相等),∠DCE=∠BEF(两直线平行,同位角相等),
∴∠DEF=∠BEF(等量代换),∴EF平分∠DEB(角平分线的定义)
24.证明:∵ , ,
∴ ,
∴EF∥CD,
∴ ,
∵ ,
∴ ,
∴DG∥BC,
∴
25.解:48
一、选择题(共30分)
1.(3分)下列图形中, 与 是对顶角的是( )
A.B.C. D.
2.(3分)如图,将一副直角三角板按照图中所示位置摆放,点C在边AO上,两条斜边互相平行,∠O=∠BCE=90°,∠A=30,∠B=45°,则∠ACB等于( )
A.15° B.20° C.25° D.30°
3.(3分)如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点,沿修建道路就能满足小路最短,这样做的依据是( )
A.垂线段最短
B.两点确定一条直线
C.两点之间,线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
4.(3分)如图,下列判断错误的是( )
A.∠1和∠2是同旁内角 B.∠3和∠4是内错角
C.∠5和∠6是同旁内角 D.∠5和∠8是同位角
5.(3分)若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不对
6.(3分)如图,已知∠B=∠AEF,则( )
A.EF∥BC B.AD∥EF C.AD∥BC D.AB∥CD
7.(3分)一把直尺和一块含30°角的直角三角板ABC按如图方式摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )
A.5° B.15° C.25° D.35°
8.(3分)有下列四个命题:①对顶角相等;②等角的补角相等;③如果b∥a,c∥a,那么b∥c;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.其中是真命题的有( )
A.4个 B.3个 C.2个 D.1个
9.(3分)如图的图案是由下列四个选项中的哪个图案平移得到的( )
A. B. C. D.
10.(3分)如图,将△ABC沿着水平方向向右平移后得到△DEF,若BC=5,CE=3,则平移的距离为( )
A.1 B.2 C.3 D.5
二、填空题(共27分)
11.(3分)如图,如果////,那么 度.
12.(3分)一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有 .(填序号)
13.(3分)如图,将木条a,b与钉在一起,,,要使木条与平行,木条转动的度数至少是 度.
14.(3分)如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是 。
15.(3分)如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若,则的度数为 .
16.(3分)把命题“平行于同一条直线的两条直线互相平行”改写成“如果…,那么…”的形式为
17.(3分)如图,已知CD平分∠ACB,DE∥AC,∠ACD=30°,则∠DEB=
18.(3分)如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为 .
19.(3分)如图:直角△ABC中,AC=3,BC=4,AB=5,则内部五个小直角三角形的周长为 .
三、解答题(共43分)
20.(8分)在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)(4分)请你作出平移后的图形△DEF;
(2)(4分)请求出△DEF的面积(每个网格是边长为1的正方形).
21.(7分)如图,射线 的端点O在直线 上, 于点O,且 平分 , 平分 ,若 ,分别求 与 的度数.
22.(7分)已知,如图,EF∥MN,且∠1=∠2,∠3=∠4,求证:AB∥CD.
23.(7分)请把下面的说理过程补充完整:
已知:如图,CD平分∠ACB,,那么EF平分∠DEB吗?请说明理由.
解:EF平分∠DEB.理由如下:
∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵(已知),
∴∠DCA= ▲ ,
∴∠DCE=∠CDE(等量代换),
∵(已知),
∴ ▲ =∠CDE( ),∠DCE=∠BEF( ),
∴ ▲ = ▲ (等量代换),
∴EF平分∠DEB( )
24.(7分)如图, , ,垂足分别为 ,且 ,求证: .
25.(7分)如图,将直角三角形ABC沿着BC方向平移到三角形DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.
答案解析部分
1.C
2.A
3.A
4.C
5.B
6.A
7.C
8.A
9.B
10.B
11.360
12.①④
13.25
14.同位角相等,两直线平行
15.
16.如果两条直线平行于同一条直线,那么这两条直线平行
17.60°
18.1200
19.12
20.(1) 如图所示,△DEF就是所求的三角形,
(2)解:△DEF的面积 =3×4-=4
21.解:∵ ,
∴∠COE=90 ,
∵ ,
∴∠BOE=20 ,
∵ 平分 ,
∴∠DOE=∠BOE=20 ,
∴∠AOE=160 ,
∵ 平分 ,
∴∠EOF=80 ,
∴∠DOF=∠EOF-∠DOE=60 .
22.解:∵EF∥MN,
∴∠2=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠BAC=180°﹣(∠1+∠2),∠DCA=180°﹣(∠3+∠4),
∴∠BAC=∠DCA,
∴AB∥CD
23.解:EF平分∠DEB.理由如下:
∵CD平分∠ACB(已知),∴∠DCA=∠DCE(角平分线的定义),
∵(已知),∴∠DCA=∠CDE,∴∠DCE=∠CDE(等量代换),
∵(已知),∴∠DEF=∠CDE(两直线平行,内错角相等),∠DCE=∠BEF(两直线平行,同位角相等),
∴∠DEF=∠BEF(等量代换),∴EF平分∠DEB(角平分线的定义)
24.证明:∵ , ,
∴ ,
∴EF∥CD,
∴ ,
∵ ,
∴ ,
∴DG∥BC,
∴
25.解:48
