多边形的内角和2
图片预览




文档简介
课件19张PPT。7.3.2多边形的内角和(2)回顾与思考1.多边形的对角线定义及计算
2.多边形的内角和公式及推导方法
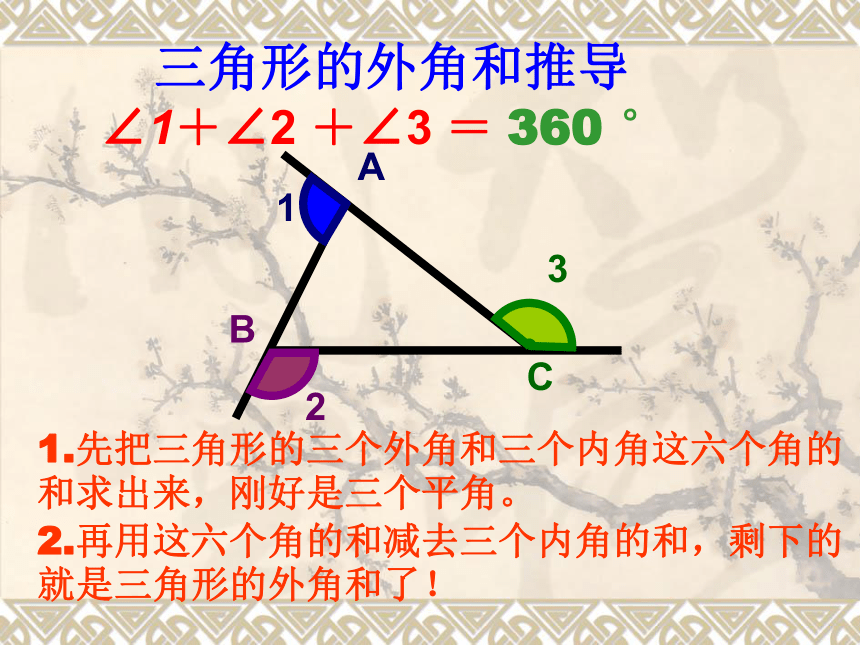
3.三角形的外角和是多少?是如何推导的?∠1+∠2 +∠3 = 360 °三角形的外角和推导1.先把三角形的三个外角和三个内角这六个角的和求出来,刚好是三个平角。
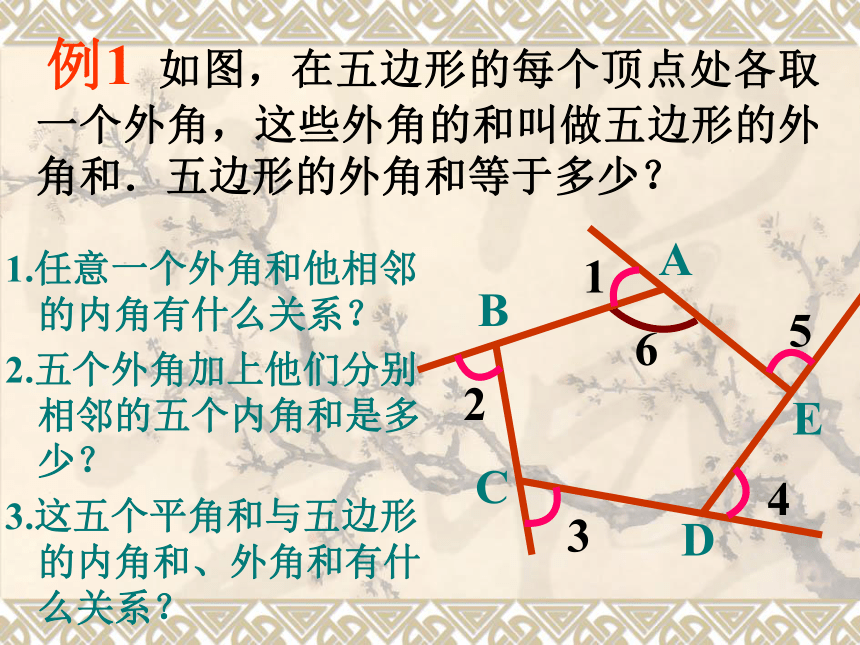
2.再用这六个角的和减去三个内角的和,剩下的就是三角形的外角和了! 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:
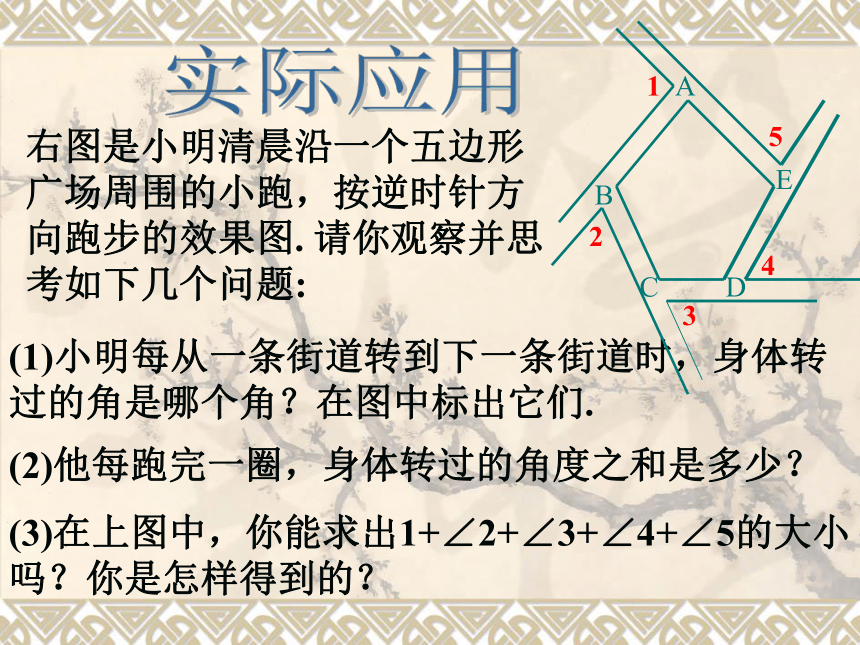
五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180°右图是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?实际应用由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:五边形的外角和等于360o 从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。解释如果广场时是六边形、七边形、八边形········
的形状,那么还有类似的结论吗?在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°
多边形的外角和都等于360°.-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °探究n边形的外角和是多少度呢?[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析[例] 一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。 例题赏析练一练如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____6解:练一练正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
练一练1、一个十边形的每一个内角都相等,那么这个
十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,则这个
多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC练一练4、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数.3、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数. 四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是多少?趣味题 将正方形截去一个角,求余下多边形的内角和度数.趣味题这节课你学到了什么?感悟与反思1.多边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 化归作 业:1.课本84页(习题7.3 )
2.A本(数学活动)
2.多边形的内角和公式及推导方法
3.三角形的外角和是多少?是如何推导的?∠1+∠2 +∠3 = 360 °三角形的外角和推导1.先把三角形的三个外角和三个内角这六个角的和求出来,刚好是三个平角。
2.再用这六个角的和减去三个内角的和,剩下的就是三角形的外角和了! 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:
五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180°右图是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?实际应用由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:五边形的外角和等于360o 从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。解释如果广场时是六边形、七边形、八边形········
的形状,那么还有类似的结论吗?在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°
多边形的外角和都等于360°.-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °探究n边形的外角和是多少度呢?[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析[例] 一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。 例题赏析练一练如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____6解:练一练正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
练一练1、一个十边形的每一个内角都相等,那么这个
十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,则这个
多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC练一练4、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数.3、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数. 四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是多少?趣味题 将正方形截去一个角,求余下多边形的内角和度数.趣味题这节课你学到了什么?感悟与反思1.多边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 化归作 业:1.课本84页(习题7.3 )
2.A本(数学活动)
