人教版七年级数学下册第五章 相交线与平行线 章节练习题 (含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线 章节练习题 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览



文档简介
七年级数学下册第五章 相交线与平行线章节练习题
一、选择题(共30分)
1.(3分)如图,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.(3分)下列四个图案中,能用平移来分析其形成过程的是( )
A. B. C. D.
3.(3分)如图,BE平分∠ABC,DE∥BC,图中相等的角共有( )
A.3对 B.4对 C.5对 D.6对
4.(3分)如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点,沿修建道路就能满足小路最短,这样做的依据是( )
A.垂线段最短
B.两点确定一条直线
C.两点之间,线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
5.(3分)下列图中,不是同位角的是( )
A. B.
C. D.
6.(3分)a,b是同一平面内不重合的两条直线,则直线a与直线b的位置关系是( )
A.一定平行 B.一定相交
C.平行或相交 D.平行且相交
7.(3分)下列图形中,能由∠1=∠2得到AB∥CD的是( )
A. B.
C. D.
8.(3分)将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
9.(3分)如图,两条平行线a,b被第三条直线c所截.若,则的度数为( )
A. B. C. D.
10.(3分)如图,将沿向右平移得到,若,,则的长是( )
A.2 B.2.5 C.3 D.5
二、填空题(共9题;共27分)
11.(3分)把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是
12.(3分)如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 °
13.(3分)如图,要使 ,则需要添加的条件是 (写出一个条件即可)
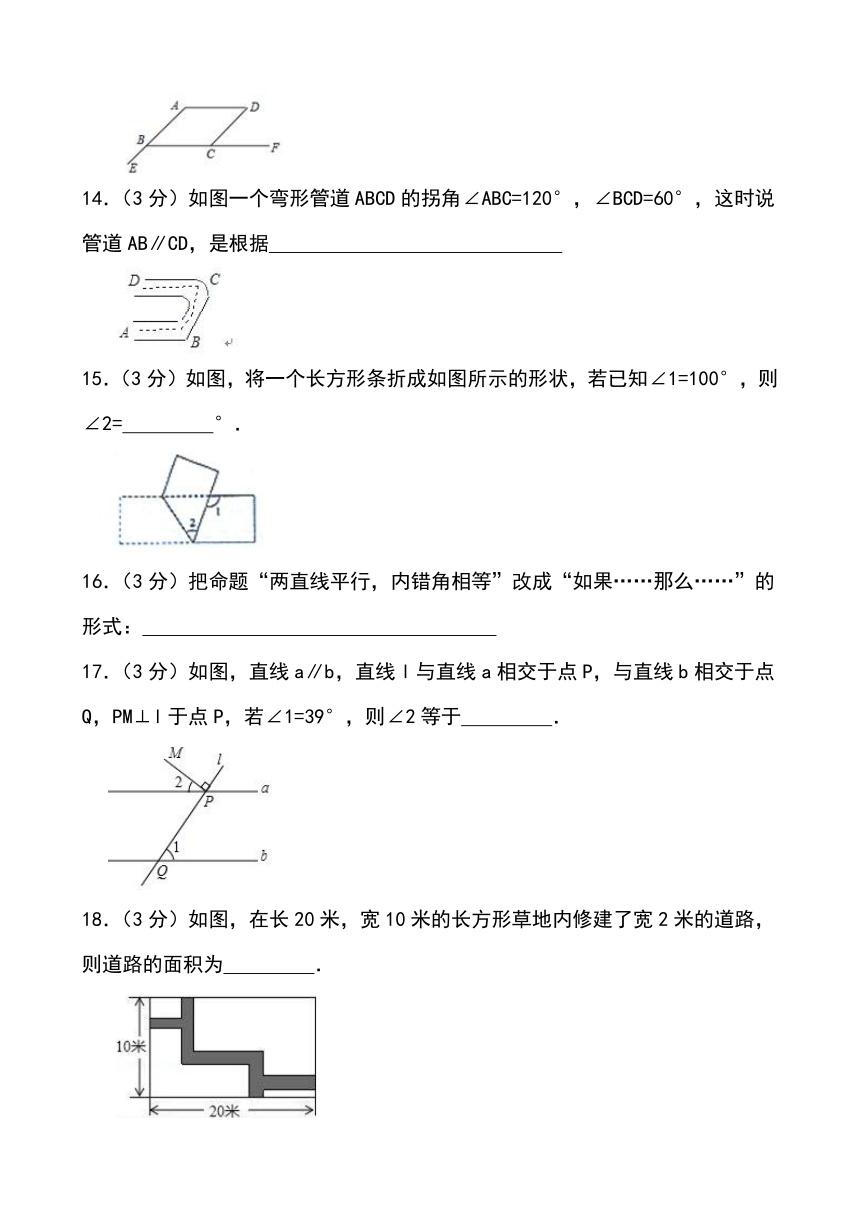
14.(3分)如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据
15.(3分)如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2= °.
16.(3分)把命题“两直线平行,内错角相等”改成“如果……那么……”的形式:
17.(3分)如图,直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于 .
18.(3分)如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则道路的面积为 .
19.(3分)如图, 沿 所在的直线平移到 的位置,且 点是线段 的中点,若 , , ,则 的长是
三、解答题(共6题;共43分)
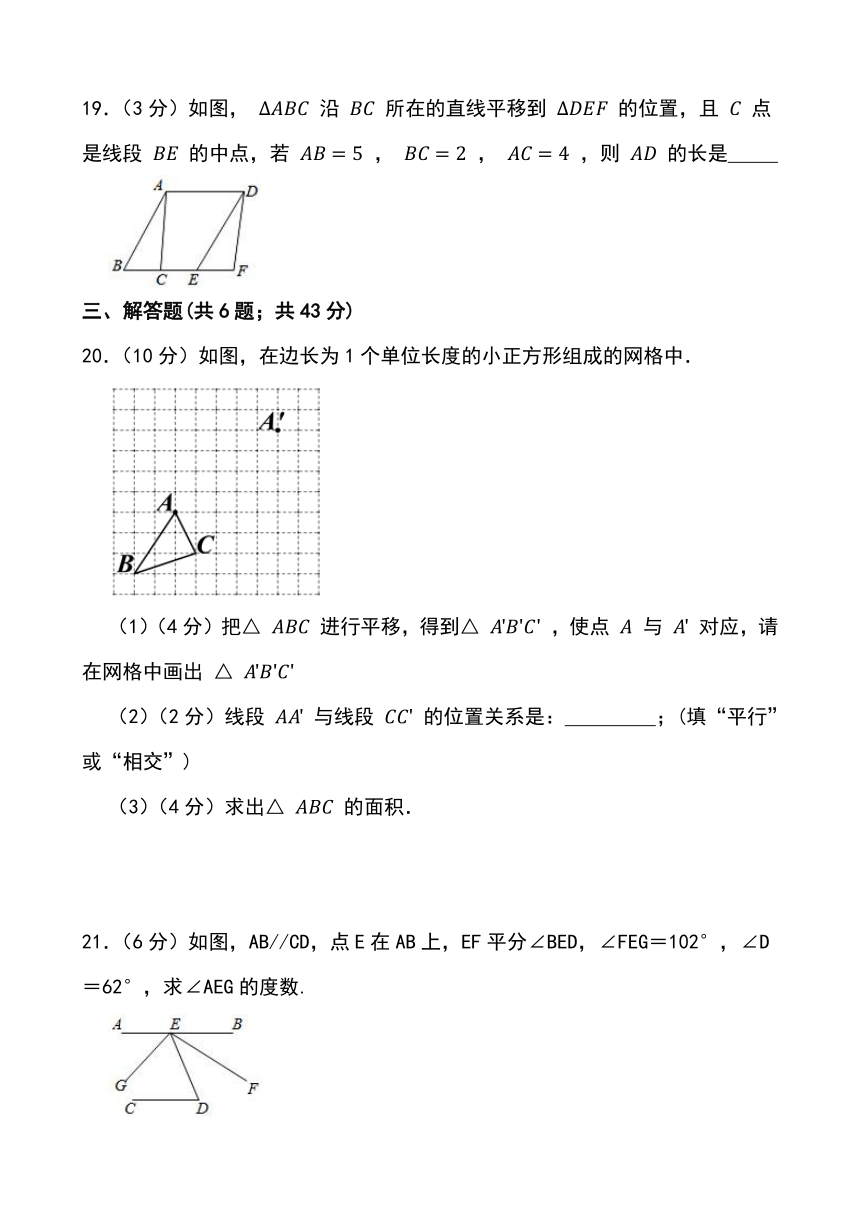
20.(10分)如图,在边长为1个单位长度的小正方形组成的网格中.
(1)(4分)把△ 进行平移,得到△ ,使点 与 对应,请在网格中画出 △
(2)(2分)线段 与线段 的位置关系是: ;(填“平行”或“相交”)
(3)(4分)求出△ 的面积.
21.(6分)如图,AB//CD,点E在AB上,EF平分∠BED,∠FEG=102°,∠D=62°,求∠AEG的度数.
22.(6分)如图,已知 ,OE平分 , , ,求 的度数。
23.(7分)填空:已知:如图, 、 、 三点在同一直线上, 、 、 三点在同一直线上, , .求证: .
证明:∵
∴ ▲ (内错角相等,两直线平行)
∴ ▲ (两直线平行,内错角相等)
∵
∴ ( ▲ )
∵
∴ ,( ▲ )
即 ▲
∴
∴ (同位角相等,两直线平行).
24.(7分)如图、点 、 均在直线 上,点 在直线 上,连接 , , 平分 交 于 ,连接 , , .求证: .
25.(7分)如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
答案解析部分
1.D
2.C
3.C
4.A
5.D
6.C
7.D
8.B
9.D
10.A
11.18°或114°
12.2
13. (或 ,或 ,或
14.同旁内角互补,两直线平行
15.50°
16.如果两直线平行,那么内错角相等
17.51°
18.56米2
19.51
20.(1)解:如图
(2)平行
(3)解: =3.5
21.解:∵AB∥CD,
∴∠BED=∠D=62°,
∵EF平分∠BED,
∴∠DEF= ∠BED=31°,
∴∠GED=∠FEG-∠DEF=102°-31°=71°,
∴∠AEG=180°-∠GED-∠BED=180°-71°-62°=47°.
∴∠AEG的度数为:47°.
22.解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
23.证明:∵∠2=∠E
∴AD∥BC(内错角相等,两直线平行)
∴∠3=∠DAC(两直线平行,内错角相等)
∵∠3=∠4
∴∠4=∠DAC(等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC
∴∠4=∠BAF
∴AB∥CD(同位角相等,两直线平行)
24.证明:∵AF平分∠BAD,
∴∠BAM=∠DAM,
∵∠DAM=∠DMA,
∴∠BAM=∠DMA,
∴AB∥CD,
∴∠B=∠DCF,
∵∠B=∠D,
∴∠D=∠DCF,
∴AD∥BC,
∴∠E=∠EFB.
25.解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积= (DW+HG) WG= (18+24)×8=168cm2.
答:阴影部分面积是168cm2.
一、选择题(共30分)
1.(3分)如图,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.(3分)下列四个图案中,能用平移来分析其形成过程的是( )
A. B. C. D.
3.(3分)如图,BE平分∠ABC,DE∥BC,图中相等的角共有( )
A.3对 B.4对 C.5对 D.6对
4.(3分)如图,现要从幸福小区修建一条连接街道的最短小路,过点作于点,沿修建道路就能满足小路最短,这样做的依据是( )
A.垂线段最短
B.两点确定一条直线
C.两点之间,线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
5.(3分)下列图中,不是同位角的是( )
A. B.
C. D.
6.(3分)a,b是同一平面内不重合的两条直线,则直线a与直线b的位置关系是( )
A.一定平行 B.一定相交
C.平行或相交 D.平行且相交
7.(3分)下列图形中,能由∠1=∠2得到AB∥CD的是( )
A. B.
C. D.
8.(3分)将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
9.(3分)如图,两条平行线a,b被第三条直线c所截.若,则的度数为( )
A. B. C. D.
10.(3分)如图,将沿向右平移得到,若,,则的长是( )
A.2 B.2.5 C.3 D.5
二、填空题(共9题;共27分)
11.(3分)把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是
12.(3分)如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 °
13.(3分)如图,要使 ,则需要添加的条件是 (写出一个条件即可)
14.(3分)如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据
15.(3分)如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2= °.
16.(3分)把命题“两直线平行,内错角相等”改成“如果……那么……”的形式:
17.(3分)如图,直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于 .
18.(3分)如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则道路的面积为 .
19.(3分)如图, 沿 所在的直线平移到 的位置,且 点是线段 的中点,若 , , ,则 的长是
三、解答题(共6题;共43分)
20.(10分)如图,在边长为1个单位长度的小正方形组成的网格中.
(1)(4分)把△ 进行平移,得到△ ,使点 与 对应,请在网格中画出 △
(2)(2分)线段 与线段 的位置关系是: ;(填“平行”或“相交”)
(3)(4分)求出△ 的面积.
21.(6分)如图,AB//CD,点E在AB上,EF平分∠BED,∠FEG=102°,∠D=62°,求∠AEG的度数.
22.(6分)如图,已知 ,OE平分 , , ,求 的度数。
23.(7分)填空:已知:如图, 、 、 三点在同一直线上, 、 、 三点在同一直线上, , .求证: .
证明:∵
∴ ▲ (内错角相等,两直线平行)
∴ ▲ (两直线平行,内错角相等)
∵
∴ ( ▲ )
∵
∴ ,( ▲ )
即 ▲
∴
∴ (同位角相等,两直线平行).
24.(7分)如图、点 、 均在直线 上,点 在直线 上,连接 , , 平分 交 于 ,连接 , , .求证: .
25.(7分)如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
答案解析部分
1.D
2.C
3.C
4.A
5.D
6.C
7.D
8.B
9.D
10.A
11.18°或114°
12.2
13. (或 ,或 ,或
14.同旁内角互补,两直线平行
15.50°
16.如果两直线平行,那么内错角相等
17.51°
18.56米2
19.51
20.(1)解:如图
(2)平行
(3)解: =3.5
21.解:∵AB∥CD,
∴∠BED=∠D=62°,
∵EF平分∠BED,
∴∠DEF= ∠BED=31°,
∴∠GED=∠FEG-∠DEF=102°-31°=71°,
∴∠AEG=180°-∠GED-∠BED=180°-71°-62°=47°.
∴∠AEG的度数为:47°.
22.解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
23.证明:∵∠2=∠E
∴AD∥BC(内错角相等,两直线平行)
∴∠3=∠DAC(两直线平行,内错角相等)
∵∠3=∠4
∴∠4=∠DAC(等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC
∴∠4=∠BAF
∴AB∥CD(同位角相等,两直线平行)
24.证明:∵AF平分∠BAD,
∴∠BAM=∠DAM,
∵∠DAM=∠DMA,
∴∠BAM=∠DMA,
∴AB∥CD,
∴∠B=∠DCF,
∵∠B=∠D,
∴∠D=∠DCF,
∴AD∥BC,
∴∠E=∠EFB.
25.解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积= (DW+HG) WG= (18+24)×8=168cm2.
答:阴影部分面积是168cm2.
