2.1 圆的对称性 课件(共38张PPT)
文档属性
| 名称 | 2.1 圆的对称性 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 17:02:59 | ||
图片预览









文档简介
(共38张PPT)
2.1 圆的对称性
1.通过观察实验操作,使学生理解圆的定义.
2.结合图形理解弧、等弧、弦、等圆、半圆、直径等有关概念.
3.圆既是轴对称图形又是中心对称图形.
4.点与圆的位置关系.
5.通过举出生活中常见圆的例子,经历观察画图的过程多角度体会和 认识圆.
6.结合本课教学特点,向学生进行爱国主义教育和美育渗透.激发学生观察、探究、发现数学问题的兴趣和欲望.
【教学重点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的理解.
【教学难点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的区别与联系.
观察
在生活中, 我们经常看到圆的形象
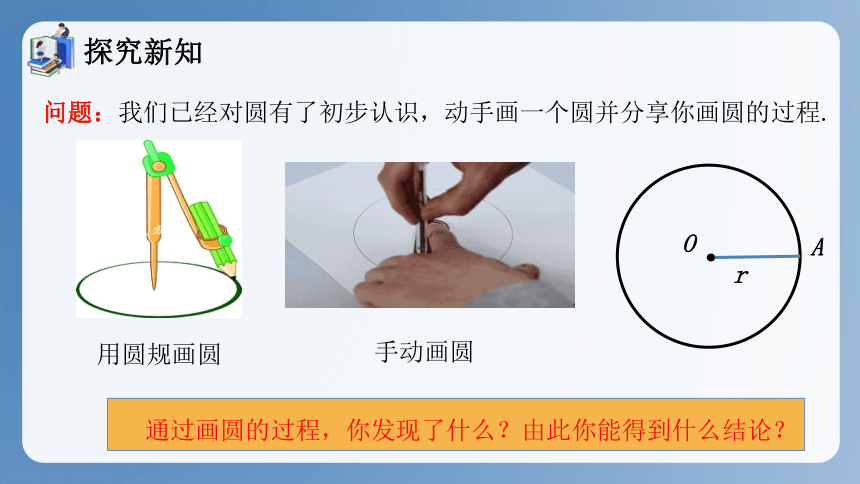
问题:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
A
O
r
手动画圆
通过画圆的过程,你发现了什么?由此你能得到什么结论?
1.圆的定义
(1)静态定义: 圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径 .
(2)动态定义: 圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径 .
特别提醒
1.确定一个圆需要 “两个要素”,一是圆心,圆心定其位置;二是半径,半径定其大小 .
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“圆上的点”指圆周上的点 .
2. 圆的表示法:
以点 O 为圆心的圆,记作⊙ O.
3. 圆的特性:
(1)圆上各点到定点(圆心 O)的距离都等于定长(半径 r) , 即同圆的半径相等 .
(2)到定点的距离等于定长的点都在同一个圆上,即到圆心的距离等于半径的点在圆上 .
1、下列条件中,能确定一个圆的是( )
A. 以点 O 为圆心
B. 以 10 cm 长为半径
C. 以点 A 为圆心,4 cm 长为半径
D. 经过已知点 M
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知A,B, D 错误;圆心和半径都确定,这样的圆有且只有一个(唯一) ,由此可知 C 正确 .
解题秘方:紧扣圆的定义的“两要素”进行判断 .
答案:C
特别提醒
1. 圆的两种定义中确定圆的条件是相同的,即圆心和半径,两者缺一不可;
2.“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上 .
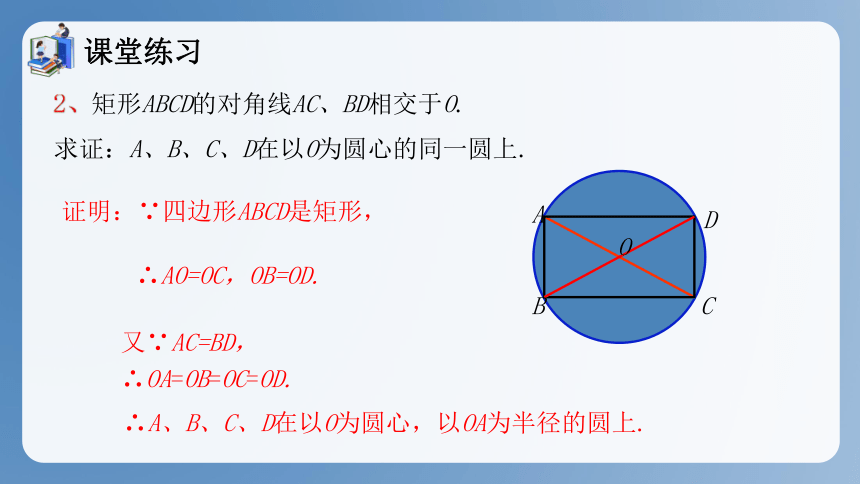
2、矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
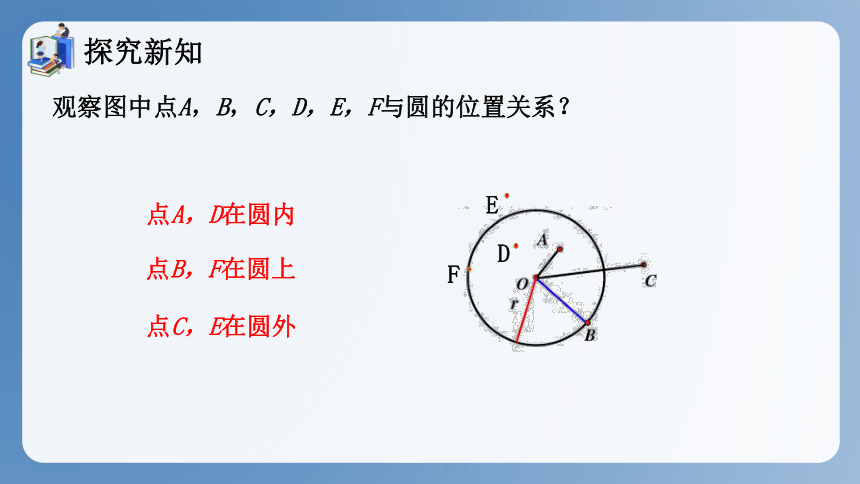
观察图中点A,B,C,D,E,F与圆的位置关系?
点A,D在圆内
点B,F在圆上
点C,E在圆外
D
E
F
我们把到圆心的距离小于半径的点叫作圆内的点;到圆心的距离大于半径的点叫作圆外的点;
等于半径的点叫做圆上的点.
圆内的点
圆外的点
圆上的点
怎样确定点与圆的位置关系?
一般地,设⊙O的半径为r,点P到圆心的距离OP=d.
点P在圆内
d点P在圆上
d=r
点P在圆外
d>r
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d左端可以推出右端,从右端也可以推出左端
数形结合:
位置关系
数量关系
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、 10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
o
圆内
圆上
圆外
D
O
A
B
C
D
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
线段 AB, CD 是⊙O 的弦, 弦AB 经过圆心 O, 因此线段 AB 是 ⊙O 的直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
B
A
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧都叫做半圆.
劣弧与优弧
C
O
A
B
半圆
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
圆上任意两点间的部分叫做圆弧,简称弧,
弧用符号“⌒”表示.
以A、B为端点的弧记作 AB ,
读作“圆弧AB”或“弧AB”.
(
D
如图中的CD
(
如图中的CAD、CAB
(
(
1、下列语句中正确的有( )
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆 .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
答案:C
解题秘方:紧扣圆的相关概念进行解答 .
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半圆是弧,半径相等的两个半圆能互相重合,所以是等弧,故③正确;只有在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确 .
警示误区
只有在同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧 .
弧不仅有长度,还有度数,规定:半圆的度数为 180°,劣 弧 的 度 数 小 于180°,优弧的度数大于 180° .
2、如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
A
B
C
E
F
D
O
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
AED,
(
ACD.
(
弦AF,AB,AC.其中弦AB又是直径.
BY YUSHEN
1. 如图 , 在一块硬纸板和一张薄的白纸上分别画一个圆 , 使它们的半径相等 , 把白纸放在硬纸板上面 , 使两个圆的圆心重合 , 观察这两个圆是否重合。
BY YUSHEN
2. 如图 , 用一根大头针穿过上述两个圆的圆心 。让硬纸板保持不动 ,让白纸绕圆心旋转任意角度 。观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合。这体现圆具有什么样的性质?
BY YUSHEN
我们把能够重合的两个圆叫作 等圆, 把能够互相重合的弧叫作 等弧 。
由于圆是由一个动点绕一个定点旋转一周所形成的图形,因此圆绕圆心旋转任意角度,都能与自身重合。
特别地,将圆绕圆心旋转 180° 时能与自身重合,所以,
圆是中心对称图形, 圆心是它的对称中心。
BY YUSHEN
如图 ,在纸上任画一个⊙ O ,并剪下来 。将 ⊙ O 沿任意一条直径 ( 例如直径 CD ) 对折, 你发现了什么?
D
O
C
圆是轴对称图形, 任意一条直径所在的直线都是圆的对称轴。
1.圆是中心对称图形,圆心是它的对称中心 .
2.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴 .
特别解读
(1)圆的对称轴有无数条 .
(2) “圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线” .
(3)直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”.
把车轮做成圆形的原因:(1)圆形易滚动;(2)车轮上各点到车轮中心轴(圆心)的距离都等于车轮的半径,当车轮滚动时,车轮轴到地面的距离保持不变,车能非常平稳地运行.
【思考】为什么通常要把车轮设计成圆形 请说说理由.
解:
1. 下面的说法对吗? 如不对, 请说明理由.
(1) 直径是弦;
(2) 弦是直径;
(3) 半径相等的两个圆是等圆;
(4) 圆既是中心对称图形, 又是轴对称图形.
√
×
不经过圆心的弦就不是直径
√
√
2.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦, 圆中以A为一个端点的优弧有 条,劣弧有 条.
A
B
C
D
O
F
E
直径
半径
一
二
四
四
3.判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)圆既是中心对称图形又是轴对称图形.
4. 已知⊙O 的半径为 4 cm,B 为线段 OA 的中点,当线段
OA 满足下列条件时,分别指出点 B 与⊙O 的位置关系:
(1) OA= 6 cm; (2) OA= 8 cm; (3) OA= 10 cm.
点 B 在圆内
点 B 在圆上
点 B 在圆外
5. 已知☉O 的半径为 6 cm , P 为线段 OA 的中点,若点 P
在☉O 上,则 OA 的长( )
A. 等于 6 cm B. 等于 12 cm
C. 小于 6 cm D. 大于 12 cm
B
6、如图 2.1-2 的图形中,不是轴对称图形的是( )
7.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE.
求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
∴B,C,D,E四个点在以点O为圆心的同一个圆上.
证明 ∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵点O为BC的中点,
∴OE=OB=OC= BC.
2
1
2
1
同理:OD=OB=OC= BC.
∴OB=OC=OD=OE.
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
二、点和圆的位置关系
设⊙O的半径为r,点P到圆心的距离为d.
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
三、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
1.布置作业:从教材“习题2.1”中选取.
2.完成同步练习册中本课时的练习.
2.1 圆的对称性
1.通过观察实验操作,使学生理解圆的定义.
2.结合图形理解弧、等弧、弦、等圆、半圆、直径等有关概念.
3.圆既是轴对称图形又是中心对称图形.
4.点与圆的位置关系.
5.通过举出生活中常见圆的例子,经历观察画图的过程多角度体会和 认识圆.
6.结合本课教学特点,向学生进行爱国主义教育和美育渗透.激发学生观察、探究、发现数学问题的兴趣和欲望.
【教学重点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的理解.
【教学难点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的区别与联系.
观察
在生活中, 我们经常看到圆的形象
问题:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
A
O
r
手动画圆
通过画圆的过程,你发现了什么?由此你能得到什么结论?
1.圆的定义
(1)静态定义: 圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径 .
(2)动态定义: 圆也可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径 .
特别提醒
1.确定一个圆需要 “两个要素”,一是圆心,圆心定其位置;二是半径,半径定其大小 .
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“圆上的点”指圆周上的点 .
2. 圆的表示法:
以点 O 为圆心的圆,记作⊙ O.
3. 圆的特性:
(1)圆上各点到定点(圆心 O)的距离都等于定长(半径 r) , 即同圆的半径相等 .
(2)到定点的距离等于定长的点都在同一个圆上,即到圆心的距离等于半径的点在圆上 .
1、下列条件中,能确定一个圆的是( )
A. 以点 O 为圆心
B. 以 10 cm 长为半径
C. 以点 A 为圆心,4 cm 长为半径
D. 经过已知点 M
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知A,B, D 错误;圆心和半径都确定,这样的圆有且只有一个(唯一) ,由此可知 C 正确 .
解题秘方:紧扣圆的定义的“两要素”进行判断 .
答案:C
特别提醒
1. 圆的两种定义中确定圆的条件是相同的,即圆心和半径,两者缺一不可;
2.“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上 .
2、矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
观察图中点A,B,C,D,E,F与圆的位置关系?
点A,D在圆内
点B,F在圆上
点C,E在圆外
D
E
F
我们把到圆心的距离小于半径的点叫作圆内的点;到圆心的距离大于半径的点叫作圆外的点;
等于半径的点叫做圆上的点.
圆内的点
圆外的点
圆上的点
怎样确定点与圆的位置关系?
一般地,设⊙O的半径为r,点P到圆心的距离OP=d.
点P在圆内
d
d=r
点P在圆外
d>r
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d
数形结合:
位置关系
数量关系
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、 10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
o
圆内
圆上
圆外
D
O
A
B
C
D
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
线段 AB, CD 是⊙O 的弦, 弦AB 经过圆心 O, 因此线段 AB 是 ⊙O 的直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
B
A
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧都叫做半圆.
劣弧与优弧
C
O
A
B
半圆
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
圆上任意两点间的部分叫做圆弧,简称弧,
弧用符号“⌒”表示.
以A、B为端点的弧记作 AB ,
读作“圆弧AB”或“弧AB”.
(
D
如图中的CD
(
如图中的CAD、CAB
(
(
1、下列语句中正确的有( )
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆 .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
答案:C
解题秘方:紧扣圆的相关概念进行解答 .
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半圆是弧,半径相等的两个半圆能互相重合,所以是等弧,故③正确;只有在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确 .
警示误区
只有在同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧 .
弧不仅有长度,还有度数,规定:半圆的度数为 180°,劣 弧 的 度 数 小 于180°,优弧的度数大于 180° .
2、如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
A
B
C
E
F
D
O
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
AED,
(
ACD.
(
弦AF,AB,AC.其中弦AB又是直径.
BY YUSHEN
1. 如图 , 在一块硬纸板和一张薄的白纸上分别画一个圆 , 使它们的半径相等 , 把白纸放在硬纸板上面 , 使两个圆的圆心重合 , 观察这两个圆是否重合。
BY YUSHEN
2. 如图 , 用一根大头针穿过上述两个圆的圆心 。让硬纸板保持不动 ,让白纸绕圆心旋转任意角度 。观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合。这体现圆具有什么样的性质?
BY YUSHEN
我们把能够重合的两个圆叫作 等圆, 把能够互相重合的弧叫作 等弧 。
由于圆是由一个动点绕一个定点旋转一周所形成的图形,因此圆绕圆心旋转任意角度,都能与自身重合。
特别地,将圆绕圆心旋转 180° 时能与自身重合,所以,
圆是中心对称图形, 圆心是它的对称中心。
BY YUSHEN
如图 ,在纸上任画一个⊙ O ,并剪下来 。将 ⊙ O 沿任意一条直径 ( 例如直径 CD ) 对折, 你发现了什么?
D
O
C
圆是轴对称图形, 任意一条直径所在的直线都是圆的对称轴。
1.圆是中心对称图形,圆心是它的对称中心 .
2.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴 .
特别解读
(1)圆的对称轴有无数条 .
(2) “圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线” .
(3)直径是弦,弦是线段,而对称轴是直线,所以不能说“圆的对称轴是直径”.
把车轮做成圆形的原因:(1)圆形易滚动;(2)车轮上各点到车轮中心轴(圆心)的距离都等于车轮的半径,当车轮滚动时,车轮轴到地面的距离保持不变,车能非常平稳地运行.
【思考】为什么通常要把车轮设计成圆形 请说说理由.
解:
1. 下面的说法对吗? 如不对, 请说明理由.
(1) 直径是弦;
(2) 弦是直径;
(3) 半径相等的两个圆是等圆;
(4) 圆既是中心对称图形, 又是轴对称图形.
√
×
不经过圆心的弦就不是直径
√
√
2.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦, 圆中以A为一个端点的优弧有 条,劣弧有 条.
A
B
C
D
O
F
E
直径
半径
一
二
四
四
3.判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)圆既是中心对称图形又是轴对称图形.
4. 已知⊙O 的半径为 4 cm,B 为线段 OA 的中点,当线段
OA 满足下列条件时,分别指出点 B 与⊙O 的位置关系:
(1) OA= 6 cm; (2) OA= 8 cm; (3) OA= 10 cm.
点 B 在圆内
点 B 在圆上
点 B 在圆外
5. 已知☉O 的半径为 6 cm , P 为线段 OA 的中点,若点 P
在☉O 上,则 OA 的长( )
A. 等于 6 cm B. 等于 12 cm
C. 小于 6 cm D. 大于 12 cm
B
6、如图 2.1-2 的图形中,不是轴对称图形的是( )
7.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE.
求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
∴B,C,D,E四个点在以点O为圆心的同一个圆上.
证明 ∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵点O为BC的中点,
∴OE=OB=OC= BC.
2
1
2
1
同理:OD=OB=OC= BC.
∴OB=OC=OD=OE.
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
二、点和圆的位置关系
设⊙O的半径为r,点P到圆心的距离为d.
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
三、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
1.布置作业:从教材“习题2.1”中选取.
2.完成同步练习册中本课时的练习.
