1.4 整式的乘法 第3课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 1.4 整式的乘法 第3课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
第一章 整式的乘除
1.4 整式的乘法
第3课时
1.能掌握多项式与多项式的乘法运算法则(重点)
2.能运用多项式与多项式乘法法则进行化简求值
一、学习目标
猜一猜下图是哪座古城的模型
二、新课导入
提示2:丝绸之路
提示1:西域
楼兰
楼兰是一个充满神秘气息的国度,你想知道它的都城楼兰城有多大吗
三、概念剖析
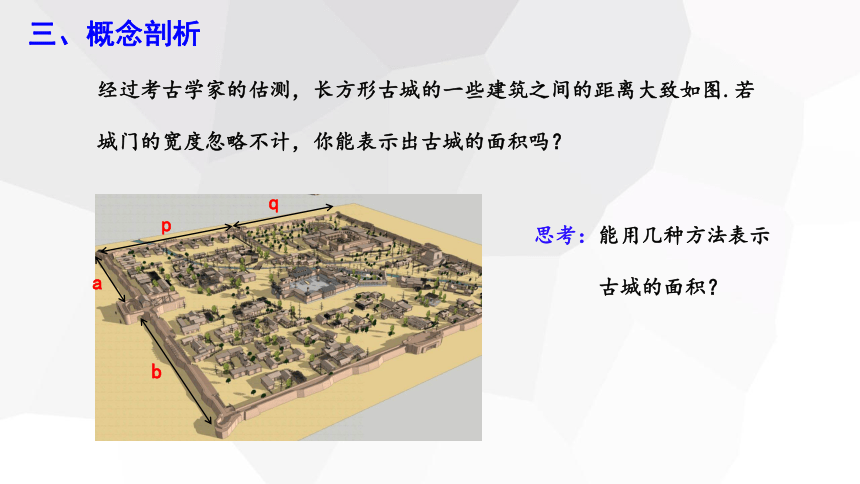
经过考古学家的估测,长方形古城的一些建筑之间的距离大致如图.若城门的宽度忽略不计,你能表示出古城的面积吗?
b
a
p
q
思考:能用几种方法表示
古城的面积?
三、概念剖析
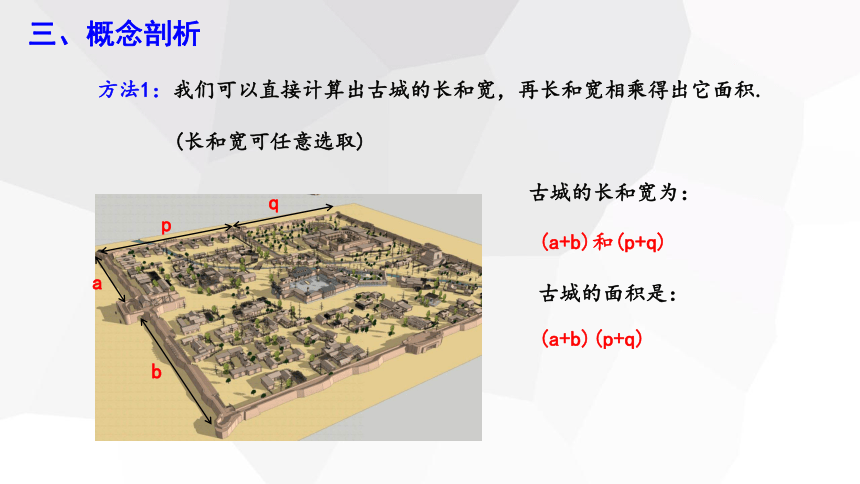
方法1:我们可以直接计算出古城的长和宽,再长和宽相乘得出它面积.
(长和宽可任意选取)
古城的长和宽为:
古城的面积是:
(a+b)和(p+q)
(a+b)(p+q)
b
a
p
q
三、概念剖析
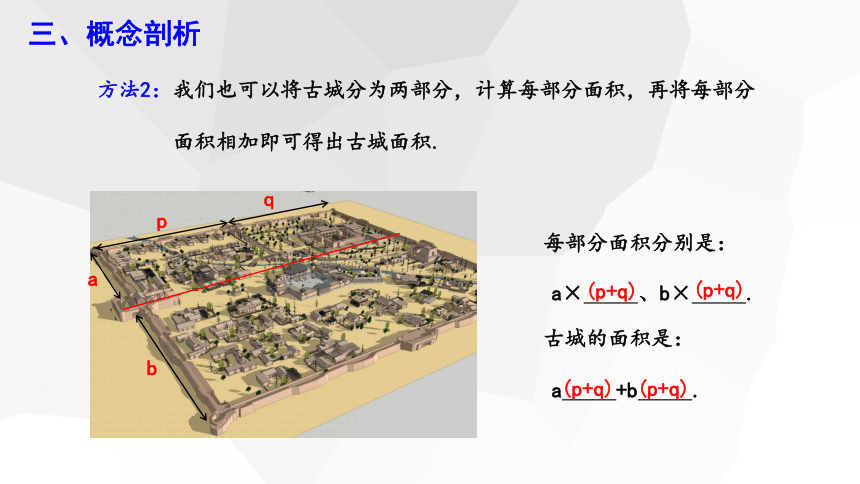
方法2:我们也可以将古城分为两部分,计算每部分面积,再将每部分
面积相加即可得出古城面积.
b
a
p
q
每部分面积分别是:
古城的面积是:
a× 、b× .
a +b .
(p+q)
(p+q)
(p+q)
(p+q)
三、概念剖析
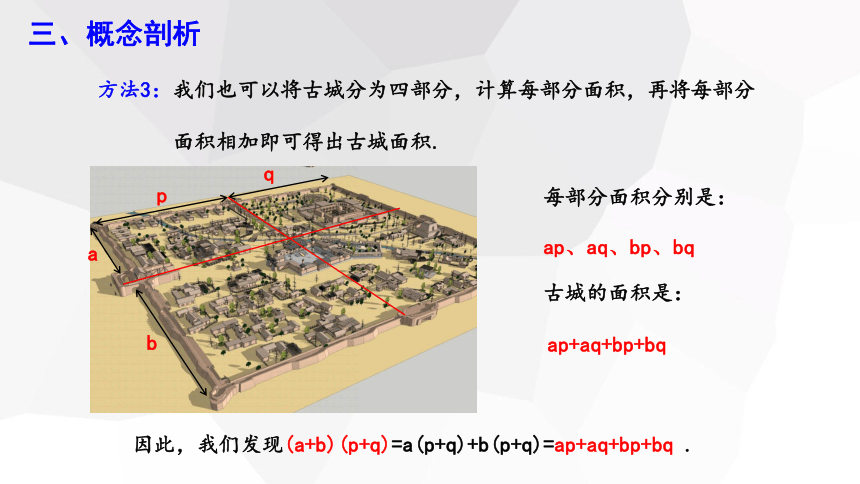
方法3:我们也可以将古城分为四部分,计算每部分面积,再将每部分
面积相加即可得出古城面积.
b
a
p
q
每部分面积分别是:
古城的面积是:
ap、aq、bp、bq
ap+aq+bp+bq
因此,我们发现(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq .
三、概念剖析
把(p+q)看成一个整体,那么两个多项式(a+b)与(p+q)相乘的问题就转化
为单项式与多项式相乘,
(a+b)
(p+q)
=
a
(p+q)
b
(p+q)
+
再利用单项式乘多项式的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq
总体来看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,
再把所得的积相加而得到,即
(a+b)(p+q)=
ap
aq
bp
bq
+
+
+
三、概念剖析
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式
的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
归纳:
可用字母表示为:(a+b)(p+q)=ap+aq+bp+bq
例1 计算:
(1)(3x+1)(x+2) (2)(x-8y)(x-y)
四、典型例题
解:(1)(3x+1)(x+2)
(2)(x-8y)(x-y)
=3x·x +3x×2+1×x+1×2
=3x2+6x+x+2
=x·x+x·(-y)+(-8y)·x+(-8y)·(-y)
=x2-xy-8xy+8y2
=x2-9xy+8y2
=3x2+7x+2
总结:多项式乘多项式结果需要化成最简形式.
1.计算.
【当堂检测】
(2)(x-2)2
(3)(3a2-1)(a-2)
(1)(3a+1)(2a+1)
(4)(a2+2a+1)(a-1)
解:(1)原式=6a2+3a+2a+1=6a2+5a+1
(2)原式=(x-2)(x-2)=x2-2x-2x+4=x2-4x+4
(3)原式=3a3-6a2-a+2
(4)原式=a3-a2+2a2-2a+a-1=a3+a2-a-1
小技巧:可将字母取值分别代入原式和答案中计算,检验计算结果是否正确.
【当堂检测】
2.找规律
(1)先计算:(x+2)(x+3)= ;
(x+1)(x-4)= ;
(x-2)(x-4)= ;
(2)通过计算结果,我们发现:
(x+a)(x+b)=( )2+( )x+( )
x2+5x+6
x2-3x-4
x2-6x+8
x
a+b
ab
实际上该结果我们由右图也可以得到
x
x
a
b
ab
ax
bx
x2
四、典型例题
例2.若多项式(x+m)与(x+1)乘积的结果中不含x的一次项,则m值为?
分析:利用多项式与多项式相乘的法则先求出结果,再进行判断.
解:(x+m)(x+1)=x2+mx+x+m=x2+(m+1)x+m,
∵乘积的结果中不含x的一次项,
∴m+1=0,∴m=-1.
故m的值为-1.
点拨:化简之后,合并同类项,如果某一项不存在,则该项的系数为0.
3.填空
(1)若ab=4,a-b=3,则代数式(2a-1)(2b+1)的值为 .
(2)已知(x+2)(x2-2ax+3)中不含x2项,a= .
【当堂检测】
解析:(1)(2a-1)(2b+1)=4ab+2a-2b-1=4ab+2(a-b)-1;
当ab=4,a-b=3,原式=4×4+2×3-1=21 .
(2)原式=x3-2ax2+3x+2x2-4ax+6=x3+(2-2a)x2-4ax+3x+6,
∵不含x2项,∴2-2a=0,∴a=1 .
21
1
五、课堂总结
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式
的每一项,再把所得的积相加.
1.多项式与多项式相乘的法则:
可用字母表示为:(a+b)(p+q)=ap+aq+bp+bq
2.注意事项:
(1)多项式与多项式相乘时不要漏项,注意正负号;
(2)结果需要化成最简形式.
第一章 整式的乘除
1.4 整式的乘法
第3课时
1.能掌握多项式与多项式的乘法运算法则(重点)
2.能运用多项式与多项式乘法法则进行化简求值
一、学习目标
猜一猜下图是哪座古城的模型
二、新课导入
提示2:丝绸之路
提示1:西域
楼兰
楼兰是一个充满神秘气息的国度,你想知道它的都城楼兰城有多大吗
三、概念剖析
经过考古学家的估测,长方形古城的一些建筑之间的距离大致如图.若城门的宽度忽略不计,你能表示出古城的面积吗?
b
a
p
q
思考:能用几种方法表示
古城的面积?
三、概念剖析
方法1:我们可以直接计算出古城的长和宽,再长和宽相乘得出它面积.
(长和宽可任意选取)
古城的长和宽为:
古城的面积是:
(a+b)和(p+q)
(a+b)(p+q)
b
a
p
q
三、概念剖析
方法2:我们也可以将古城分为两部分,计算每部分面积,再将每部分
面积相加即可得出古城面积.
b
a
p
q
每部分面积分别是:
古城的面积是:
a× 、b× .
a +b .
(p+q)
(p+q)
(p+q)
(p+q)
三、概念剖析
方法3:我们也可以将古城分为四部分,计算每部分面积,再将每部分
面积相加即可得出古城面积.
b
a
p
q
每部分面积分别是:
古城的面积是:
ap、aq、bp、bq
ap+aq+bp+bq
因此,我们发现(a+b)(p+q)=a(p+q)+b(p+q)=ap+aq+bp+bq .
三、概念剖析
把(p+q)看成一个整体,那么两个多项式(a+b)与(p+q)相乘的问题就转化
为单项式与多项式相乘,
(a+b)
(p+q)
=
a
(p+q)
b
(p+q)
+
再利用单项式乘多项式的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq
总体来看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,
再把所得的积相加而得到,即
(a+b)(p+q)=
ap
aq
bp
bq
+
+
+
三、概念剖析
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式
的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
归纳:
可用字母表示为:(a+b)(p+q)=ap+aq+bp+bq
例1 计算:
(1)(3x+1)(x+2) (2)(x-8y)(x-y)
四、典型例题
解:(1)(3x+1)(x+2)
(2)(x-8y)(x-y)
=3x·x +3x×2+1×x+1×2
=3x2+6x+x+2
=x·x+x·(-y)+(-8y)·x+(-8y)·(-y)
=x2-xy-8xy+8y2
=x2-9xy+8y2
=3x2+7x+2
总结:多项式乘多项式结果需要化成最简形式.
1.计算.
【当堂检测】
(2)(x-2)2
(3)(3a2-1)(a-2)
(1)(3a+1)(2a+1)
(4)(a2+2a+1)(a-1)
解:(1)原式=6a2+3a+2a+1=6a2+5a+1
(2)原式=(x-2)(x-2)=x2-2x-2x+4=x2-4x+4
(3)原式=3a3-6a2-a+2
(4)原式=a3-a2+2a2-2a+a-1=a3+a2-a-1
小技巧:可将字母取值分别代入原式和答案中计算,检验计算结果是否正确.
【当堂检测】
2.找规律
(1)先计算:(x+2)(x+3)= ;
(x+1)(x-4)= ;
(x-2)(x-4)= ;
(2)通过计算结果,我们发现:
(x+a)(x+b)=( )2+( )x+( )
x2+5x+6
x2-3x-4
x2-6x+8
x
a+b
ab
实际上该结果我们由右图也可以得到
x
x
a
b
ab
ax
bx
x2
四、典型例题
例2.若多项式(x+m)与(x+1)乘积的结果中不含x的一次项,则m值为?
分析:利用多项式与多项式相乘的法则先求出结果,再进行判断.
解:(x+m)(x+1)=x2+mx+x+m=x2+(m+1)x+m,
∵乘积的结果中不含x的一次项,
∴m+1=0,∴m=-1.
故m的值为-1.
点拨:化简之后,合并同类项,如果某一项不存在,则该项的系数为0.
3.填空
(1)若ab=4,a-b=3,则代数式(2a-1)(2b+1)的值为 .
(2)已知(x+2)(x2-2ax+3)中不含x2项,a= .
【当堂检测】
解析:(1)(2a-1)(2b+1)=4ab+2a-2b-1=4ab+2(a-b)-1;
当ab=4,a-b=3,原式=4×4+2×3-1=21 .
(2)原式=x3-2ax2+3x+2x2-4ax+6=x3+(2-2a)x2-4ax+3x+6,
∵不含x2项,∴2-2a=0,∴a=1 .
21
1
五、课堂总结
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式
的每一项,再把所得的积相加.
1.多项式与多项式相乘的法则:
可用字母表示为:(a+b)(p+q)=ap+aq+bp+bq
2.注意事项:
(1)多项式与多项式相乘时不要漏项,注意正负号;
(2)结果需要化成最简形式.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
