2.1 两条直线的位置关系 第2课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 2.1 两条直线的位置关系 第2课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
第二章 相交线与平行线
2.1 两条直线的位置关系
第2课时
一、学习目标
1.能理解垂直与垂足的概念,会用几何符号表示垂直关系
2.能掌握垂线的相关性质,会作点到直线的距离
二、新课导入
观察下列几幅图
礼物包装带
道路
教堂
不难发现图中相交的线条,但它们有些特殊,形状类似于“十”字.
三、概念剖析
(一)垂线的相关概念
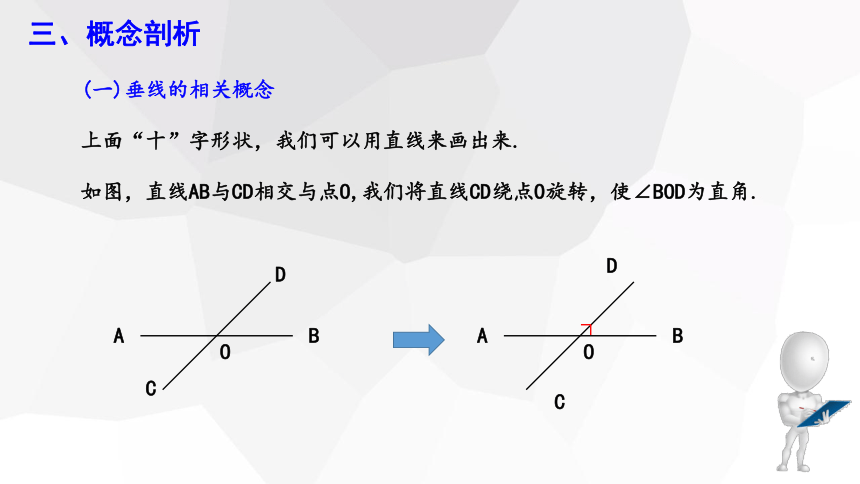
上面“十”字形状,我们可以用直线来画出来.
A
B
C
D
O
A
B
C
D
O
如图,直线AB与CD相交与点O,我们将直线CD绕点O旋转,使∠BOD为直角.
三、概念剖析
A
B
C
D
O
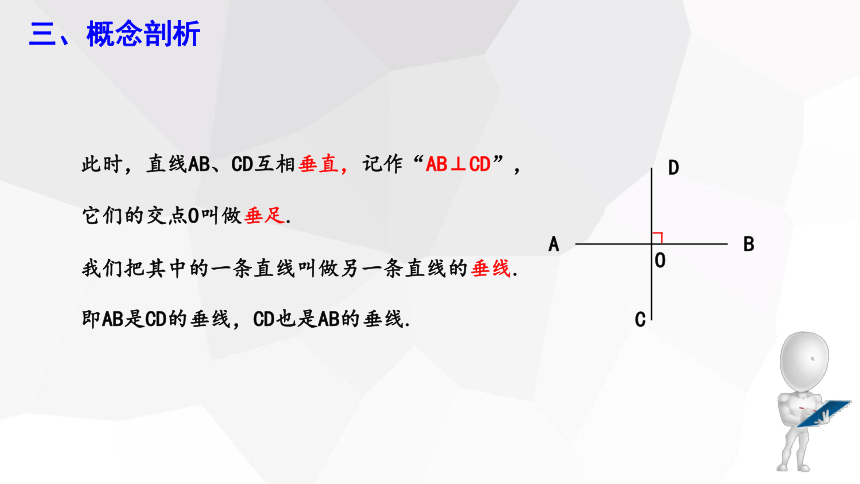
此时,直线AB、CD互相垂直,记作“AB⊥CD”,
它们的交点O叫做垂足.
我们把其中的一条直线叫做另一条直线的垂线.
即AB是CD的垂线,CD也是AB的垂线.
三、概念剖析
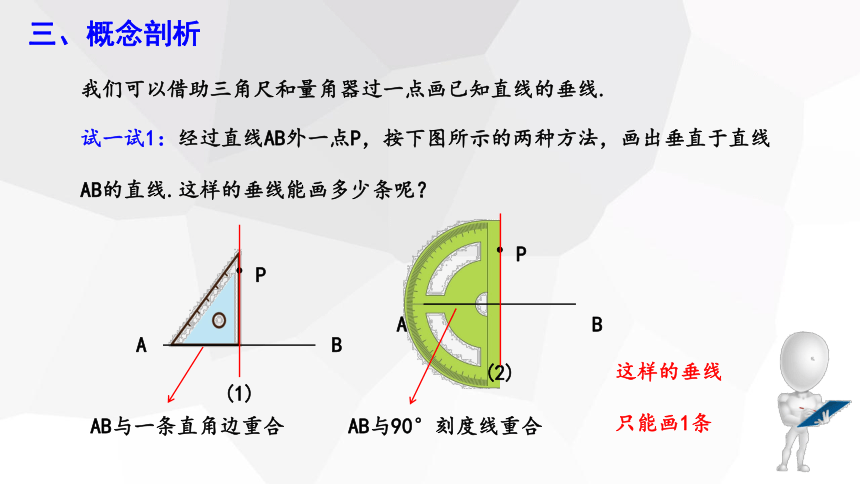
我们可以借助三角尺和量角器过一点画已知直线的垂线.
试一试1:经过直线AB外一点P,按下图所示的两种方法,画出垂直于直线
AB的直线.这样的垂线能画多少条呢?
A
B
(1)
P
A
B
(2)
P
AB与一条直角边重合
AB与90°刻度线重合
这样的垂线
只能画1条
三、概念剖析
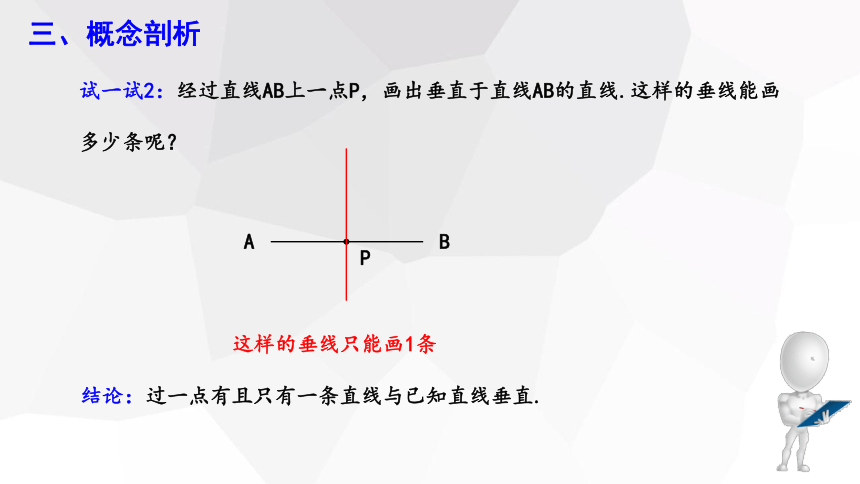
试一试2:经过直线AB上一点P,画出垂直于直线AB的直线.这样的垂线能画
多少条呢?
A
B
P
这样的垂线只能画1条
结论:过一点有且只有一条直线与已知直线垂直.
三、概念剖析
(二)点到直线的距离
观察:如图,点P是直线m外一点,A、B、C、D是直线m上的4个点,其中PB与
直线m垂直,垂足为点B.线段PA、PB、PC、PD谁最短?
A
B
m
C
D
P
线段PB最短
我们把线段PB叫做点P到直线m的垂线段.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
三、概念剖析
A
B
m
C
D
P
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
例如,线段PB的长度就是点P到直线m的距离.
四、典型例题
例1.如图所示,直线AC和直线BD相交与点O,∠AOD=90°.
A
B
C
D
O
(1)∠COD= ,∠BOC= ,∠AOB= .
(2)直线AC与直线BD ,0点为 ,记作 .
(3)直线AC是直线BD的 ,直线BD是直线AC的 .
90°
90°
90°
垂直
垂足
AC⊥BD
垂线
垂线
(4)线段AO是A点到直线BD的 ,B点到AC的距离为线段 的长度.
垂线段
BO
【当堂检测】
1.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是 .
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;
④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;
⑥线段AC的长度是点A到BC的距离.
B
D
A
C
①④⑤⑥
解析:∵∠ACB=90°,∴AC⊥BC,故①正确;AC与DC相交不垂直,故②错误;
点A到BC的垂线段是线段AC,故③错误;点C到AB的垂线段是线段CD,故④正确;
线段BC的长度是点B到AC的距离,故⑤正确;
线段AC的长度是点A到BC的距离,故⑥正确.
【当堂检测】
2.如图,已知AB⊥CD,垂足为点O,直线EF经过点O,若∠1=35°,则∠AOE的度数为 .
A
D
B
C
O
E
F
1
55°
解析:∵AB⊥CD,
∴∠BOC=90°,
∵∠1=35°,
∴∠FOB=90°-35°=55°,
∴∠AOE=∠FOB=55°,
四、典型例题
例2.如图,直线AB、直线BC、直线AC两两相交,交点为点A,点B、点C,
∠ABC=90°,AC=10,AB=6,求点A到直线BC的距离.
A
C
B
分析:根据题意可知AB为A点到直线BC的垂线段,故点A到
直线BC的距离为线段AB的长度.
解:∵∠ABC=90°,
∴直线AB⊥直线BC,B点为垂足.
∴AB为A点到直线BC的垂线段.
∴A到直线BC的距离为线段AB的长度.
∴A到直线BC的距离为6.
【当堂检测】
3.如图,已知OM⊥a,ON⊥a,
(1)OM与ON重合的理由是: .
(2)若N为线段OM的中点,ON=3,则M点到直线a的距离为 .
N
a
M
O
过一点有且只有一条直线与已知直线垂直
6
五、课堂总结
当两条直线相交所构成的四个角中有一个为直角,那么这两条直线互相垂直.
1.垂直的定义:
表示方法:
直线AB、CD互相垂直,记作“AB⊥CD”.
2.垂线的性质:
平面内,过一点有且只有一条直线与已知直线垂直.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
第二章 相交线与平行线
2.1 两条直线的位置关系
第2课时
一、学习目标
1.能理解垂直与垂足的概念,会用几何符号表示垂直关系
2.能掌握垂线的相关性质,会作点到直线的距离
二、新课导入
观察下列几幅图
礼物包装带
道路
教堂
不难发现图中相交的线条,但它们有些特殊,形状类似于“十”字.
三、概念剖析
(一)垂线的相关概念
上面“十”字形状,我们可以用直线来画出来.
A
B
C
D
O
A
B
C
D
O
如图,直线AB与CD相交与点O,我们将直线CD绕点O旋转,使∠BOD为直角.
三、概念剖析
A
B
C
D
O
此时,直线AB、CD互相垂直,记作“AB⊥CD”,
它们的交点O叫做垂足.
我们把其中的一条直线叫做另一条直线的垂线.
即AB是CD的垂线,CD也是AB的垂线.
三、概念剖析
我们可以借助三角尺和量角器过一点画已知直线的垂线.
试一试1:经过直线AB外一点P,按下图所示的两种方法,画出垂直于直线
AB的直线.这样的垂线能画多少条呢?
A
B
(1)
P
A
B
(2)
P
AB与一条直角边重合
AB与90°刻度线重合
这样的垂线
只能画1条
三、概念剖析
试一试2:经过直线AB上一点P,画出垂直于直线AB的直线.这样的垂线能画
多少条呢?
A
B
P
这样的垂线只能画1条
结论:过一点有且只有一条直线与已知直线垂直.
三、概念剖析
(二)点到直线的距离
观察:如图,点P是直线m外一点,A、B、C、D是直线m上的4个点,其中PB与
直线m垂直,垂足为点B.线段PA、PB、PC、PD谁最短?
A
B
m
C
D
P
线段PB最短
我们把线段PB叫做点P到直线m的垂线段.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
三、概念剖析
A
B
m
C
D
P
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
例如,线段PB的长度就是点P到直线m的距离.
四、典型例题
例1.如图所示,直线AC和直线BD相交与点O,∠AOD=90°.
A
B
C
D
O
(1)∠COD= ,∠BOC= ,∠AOB= .
(2)直线AC与直线BD ,0点为 ,记作 .
(3)直线AC是直线BD的 ,直线BD是直线AC的 .
90°
90°
90°
垂直
垂足
AC⊥BD
垂线
垂线
(4)线段AO是A点到直线BD的 ,B点到AC的距离为线段 的长度.
垂线段
BO
【当堂检测】
1.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是 .
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;
④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;
⑥线段AC的长度是点A到BC的距离.
B
D
A
C
①④⑤⑥
解析:∵∠ACB=90°,∴AC⊥BC,故①正确;AC与DC相交不垂直,故②错误;
点A到BC的垂线段是线段AC,故③错误;点C到AB的垂线段是线段CD,故④正确;
线段BC的长度是点B到AC的距离,故⑤正确;
线段AC的长度是点A到BC的距离,故⑥正确.
【当堂检测】
2.如图,已知AB⊥CD,垂足为点O,直线EF经过点O,若∠1=35°,则∠AOE的度数为 .
A
D
B
C
O
E
F
1
55°
解析:∵AB⊥CD,
∴∠BOC=90°,
∵∠1=35°,
∴∠FOB=90°-35°=55°,
∴∠AOE=∠FOB=55°,
四、典型例题
例2.如图,直线AB、直线BC、直线AC两两相交,交点为点A,点B、点C,
∠ABC=90°,AC=10,AB=6,求点A到直线BC的距离.
A
C
B
分析:根据题意可知AB为A点到直线BC的垂线段,故点A到
直线BC的距离为线段AB的长度.
解:∵∠ABC=90°,
∴直线AB⊥直线BC,B点为垂足.
∴AB为A点到直线BC的垂线段.
∴A到直线BC的距离为线段AB的长度.
∴A到直线BC的距离为6.
【当堂检测】
3.如图,已知OM⊥a,ON⊥a,
(1)OM与ON重合的理由是: .
(2)若N为线段OM的中点,ON=3,则M点到直线a的距离为 .
N
a
M
O
过一点有且只有一条直线与已知直线垂直
6
五、课堂总结
当两条直线相交所构成的四个角中有一个为直角,那么这两条直线互相垂直.
1.垂直的定义:
表示方法:
直线AB、CD互相垂直,记作“AB⊥CD”.
2.垂线的性质:
平面内,过一点有且只有一条直线与已知直线垂直.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
