3.3 用图象表示的变量间关系 第1课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 3.3 用图象表示的变量间关系 第1课时 课件 (共15张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:27:57 | ||
图片预览





文档简介
(共15张PPT)
第三章 变量之间的关系
3.3 用图象表示的变量间关系
第1课时
1.能理解图象上的点所表示的实际意义(重点)
2.能体会变量之间的关系
一、学习目标
二、新课导入
复习回顾:
假设圆柱的高是2cm,当圆柱的底面半径由小到大变化时:
(1)圆柱的体积是如何变化?在这个变化中,自变量、因变量是什么?
(2)如果圆柱底面半径为r(cm),圆柱的体积V可以表示为 ;
(3)当r由1cm变化到10cm时,V由 变化到 。
圆柱体积也在不断变大;自变量是底面半径,因变量是体积
三、概念剖析
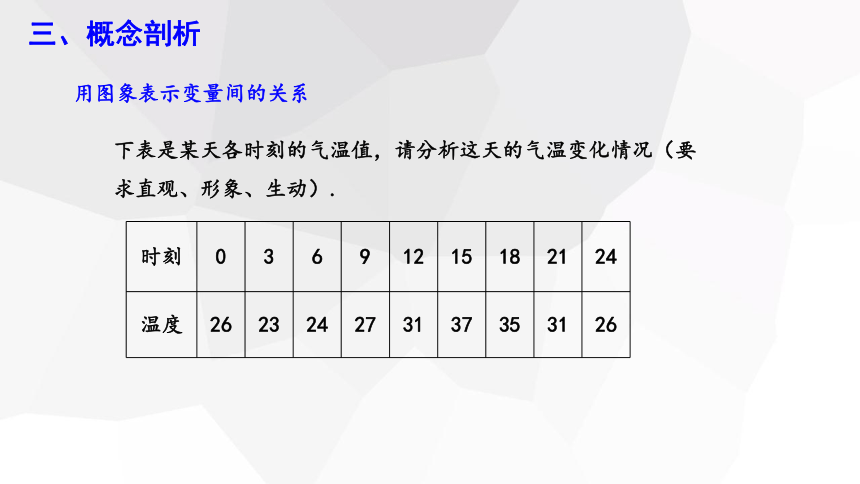
下表是某天各时刻的气温值,请分析这天的气温变化情况(要求直观、形象、生动).
时刻 0 3 6 9 12 15 18 21 24
温度 26 23 24 27 31 37 35 31 26
用图象表示变量间的关系
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
三、概念剖析
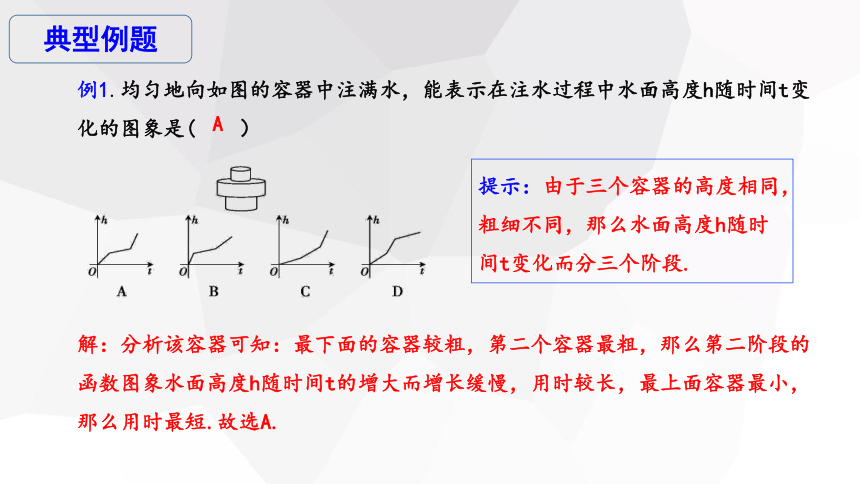
例1.均匀地向如图的容器中注满水,能表示在注水过程中水面高度h随时间t变化的图象是( )
A
解:分析该容器可知:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.故选A.
提示:由于三个容器的高度相同,粗细不同,那么水面高度h随时间t变化而分三个阶段.
典型例题
典型例题
归纳总结:
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
1.下列各图分别近似地刻画了现实生活中两变量之间的变化关系,其中,能大致刻画张老师从住家小区单元的2楼坐电梯到5楼(中途不停)中高度与时间关系的变化图是( )
【当堂检测】
B
例2.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,中间经过丙港,如下图是这艘轮船离开甲港的距离随时间的变化曲线.
①从甲港(0)出发到达丙港(A),需用多长时间?
解:看图可知:从甲港(0)出发到达丙港(A)需用1个小时.
②从丙港(A)到达乙港(C),需用多长时间?
从丙港(A)到达乙港(C),需用2个小时.
(1)观察曲线回答下列问题:
典型例题
③图中CD段表示什么情况,船在乙港停留多长时间?返回时,多长时间到达丙港(B)?
CD段表示船在乙港(C)停留,
船在乙港停留了1个小时,
返回时4个小时到达丙港(B).
④从丙港(B)返回到出发点甲港(E),用多长时间?
从丙港(B)返回到出发点甲港(E)用了2个小时.
典型例题
(2)轮船从甲港前往乙港的平均行驶速度快,还是轮船返回的平均速度快呢?
轮船从甲港前往乙港的平均行驶速度快.
(3)如果轮船往返的机器速度是一样的,那么从甲港到乙港是顺水还是逆水?
从甲港到乙港是顺水.
典型例题
1.借助图象,过某点分别向横轴、纵轴作垂线可以知道自变量取某个值时,因变量取什么值。
2.观察图象的关键是要抓住图象的最高点与最低点以及这些点所对应的自变量与因变量的值,利用图象可判断因变量的变化趋势。
典型例题
归纳总结:
2.研究表明,温度对生猪饲养有一定的影响.下图是某生猪饲养场查阅的下周天气预报情况,根据图中信息回答下列问题:
(1)周二的最高气温与最低气温分别是多少?
(2)图中点A表示的实际意义是什么?
【当堂检测】
解:(1)周二的最高气温是18℃,最低气温是5℃;
(2)图中点A表示的实际意义是周五的最高气温是25℃;
【当堂检测】
(3)当一天内的温差超过12℃时,生猪可能出现生理异常.为了预防生猪生理异常,养殖场需要在哪几天进行人工调节温度?
解:(3)周一温差是13-4=9℃,周二温差是18-5=13℃,周三温差是16-10=6℃,周四温差是23-12=11℃,周五温差是25-11=14℃,周六温差是21-8=13℃,周日温差是15-7=8℃.
因为当一天内的温差超过12℃时,生猪可能出现生理异常,
所以为了预防生猪生理异常,养殖场需要在周二、周五、周六这三天进行人工调节温度.
四、课堂总结
1.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
2.借助图象,过某点分别向横轴、纵轴作垂线可以知道自变量取某个值时,因变量取什么值.
3.观察图象的关键是要抓住图象的最高点与最低点以及这些点所对应的自变量与因变量的值,利用图象可判断因变量的变化趋势.
第三章 变量之间的关系
3.3 用图象表示的变量间关系
第1课时
1.能理解图象上的点所表示的实际意义(重点)
2.能体会变量之间的关系
一、学习目标
二、新课导入
复习回顾:
假设圆柱的高是2cm,当圆柱的底面半径由小到大变化时:
(1)圆柱的体积是如何变化?在这个变化中,自变量、因变量是什么?
(2)如果圆柱底面半径为r(cm),圆柱的体积V可以表示为 ;
(3)当r由1cm变化到10cm时,V由 变化到 。
圆柱体积也在不断变大;自变量是底面半径,因变量是体积
三、概念剖析
下表是某天各时刻的气温值,请分析这天的气温变化情况(要求直观、形象、生动).
时刻 0 3 6 9 12 15 18 21 24
温度 26 23 24 27 31 37 35 31 26
用图象表示变量间的关系
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
三、概念剖析
例1.均匀地向如图的容器中注满水,能表示在注水过程中水面高度h随时间t变化的图象是( )
A
解:分析该容器可知:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.故选A.
提示:由于三个容器的高度相同,粗细不同,那么水面高度h随时间t变化而分三个阶段.
典型例题
典型例题
归纳总结:
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
1.下列各图分别近似地刻画了现实生活中两变量之间的变化关系,其中,能大致刻画张老师从住家小区单元的2楼坐电梯到5楼(中途不停)中高度与时间关系的变化图是( )
【当堂检测】
B
例2.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,中间经过丙港,如下图是这艘轮船离开甲港的距离随时间的变化曲线.
①从甲港(0)出发到达丙港(A),需用多长时间?
解:看图可知:从甲港(0)出发到达丙港(A)需用1个小时.
②从丙港(A)到达乙港(C),需用多长时间?
从丙港(A)到达乙港(C),需用2个小时.
(1)观察曲线回答下列问题:
典型例题
③图中CD段表示什么情况,船在乙港停留多长时间?返回时,多长时间到达丙港(B)?
CD段表示船在乙港(C)停留,
船在乙港停留了1个小时,
返回时4个小时到达丙港(B).
④从丙港(B)返回到出发点甲港(E),用多长时间?
从丙港(B)返回到出发点甲港(E)用了2个小时.
典型例题
(2)轮船从甲港前往乙港的平均行驶速度快,还是轮船返回的平均速度快呢?
轮船从甲港前往乙港的平均行驶速度快.
(3)如果轮船往返的机器速度是一样的,那么从甲港到乙港是顺水还是逆水?
从甲港到乙港是顺水.
典型例题
1.借助图象,过某点分别向横轴、纵轴作垂线可以知道自变量取某个值时,因变量取什么值。
2.观察图象的关键是要抓住图象的最高点与最低点以及这些点所对应的自变量与因变量的值,利用图象可判断因变量的变化趋势。
典型例题
归纳总结:
2.研究表明,温度对生猪饲养有一定的影响.下图是某生猪饲养场查阅的下周天气预报情况,根据图中信息回答下列问题:
(1)周二的最高气温与最低气温分别是多少?
(2)图中点A表示的实际意义是什么?
【当堂检测】
解:(1)周二的最高气温是18℃,最低气温是5℃;
(2)图中点A表示的实际意义是周五的最高气温是25℃;
【当堂检测】
(3)当一天内的温差超过12℃时,生猪可能出现生理异常.为了预防生猪生理异常,养殖场需要在哪几天进行人工调节温度?
解:(3)周一温差是13-4=9℃,周二温差是18-5=13℃,周三温差是16-10=6℃,周四温差是23-12=11℃,周五温差是25-11=14℃,周六温差是21-8=13℃,周日温差是15-7=8℃.
因为当一天内的温差超过12℃时,生猪可能出现生理异常,
所以为了预防生猪生理异常,养殖场需要在周二、周五、周六这三天进行人工调节温度.
四、课堂总结
1.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
2.借助图象,过某点分别向横轴、纵轴作垂线可以知道自变量取某个值时,因变量取什么值.
3.观察图象的关键是要抓住图象的最高点与最低点以及这些点所对应的自变量与因变量的值,利用图象可判断因变量的变化趋势.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
