4.5 利用三角形全等测距离 课件(共14张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 4.5 利用三角形全等测距离 课件(共14张PPT) 2023-2024学年初中数学北师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 403.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:31:08 | ||
图片预览





文档简介
(共14张PPT)
第四章 三角形
4.5 利用三角形全等测距离
1.能运用三角形全等测量距离,解决实际生活中的相关问题.
2.掌握三角形全等性质的应用.(重点)
一、学习目标
二、新课导入
回顾:
我们已经学过判定全等三角形的方法有哪些?
全等三角形的性质:
全等三角形对应边相等,对应角相等.
SSS
SAS
ASA
AAS
三、概念剖析
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离.由于没有任何测量工具,我八路军战士为
此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功.
利用三角形全等测距离
三、概念剖析
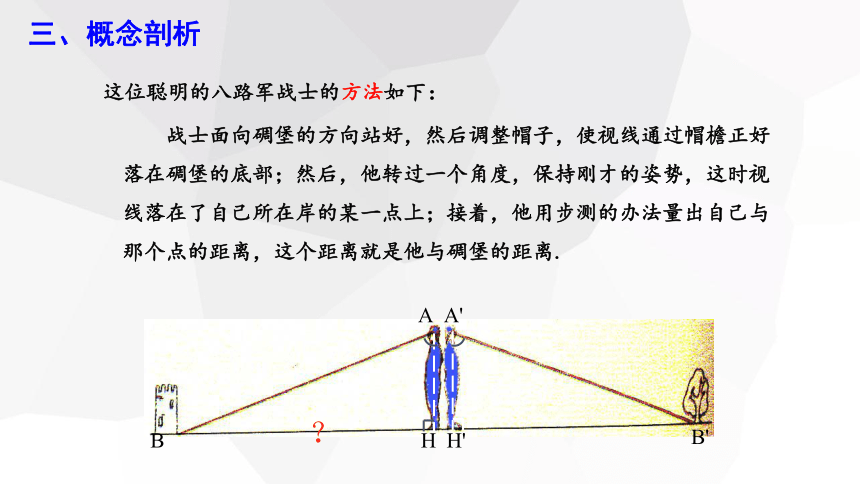
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
A
H
A'
H'
B
B'
?
三、概念剖析
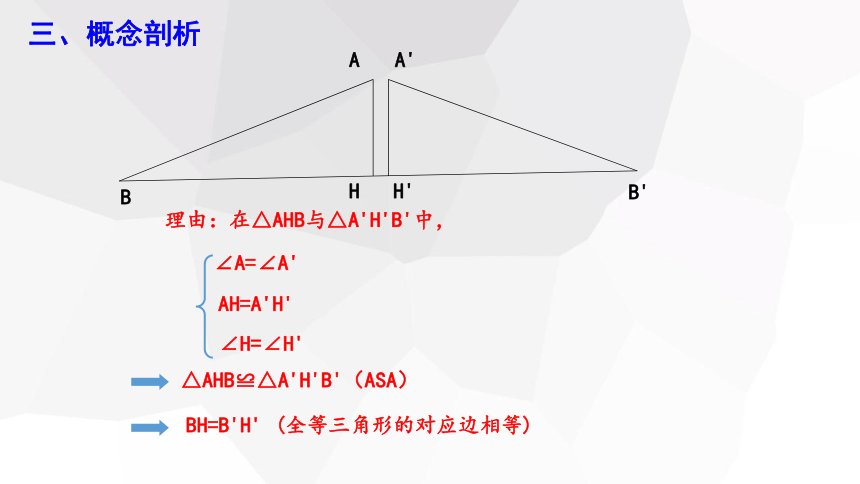
理由:在△AHB与△A'H'B'中,
∠A=∠A'
AH=A'H'
∠H=∠H'
△AHB≌△A'H'B'(ASA)
BH=B'H'
A
A'
B
B'
H'
H
(全等三角形的对应边相等)
三、概念剖析
根据上述例子我们得出结论:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
例1.小强为了测量一栋高楼的高度AB,在旗杆CD与楼之间选定一点P.测得在P点观察旗杆顶C的视线PC与地面的夹角∠DPC=36°,测得在P点观察楼顶A的视线PA与地面的夹角∠APB=54°,量得P到楼底的距离PB与旗杆的高度相等,均为10米,量得旗杆与楼之间的距离DB=36米,如图,小强计算出了楼高,楼高AB是多少米?
分析:根据题意可得△CPD≌△PAB,进而利用AB=DP=DB-PB求出楼高.
典型例题
解:∵∠DPC=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵
∴△CPD≌△PAB(ASA),∴PD=AB,
∵DB=36,PB=10,∴AB=36-10=26(m),
答:楼高AB是26米.
∠CDP=∠PBA
DC=PB
∠DCP=∠BPA
典型例题
如何求未知线段?
途径:利用三角形全等
方法:转化思想
典型例题
归纳总结:
【当堂检测】
1.如图所示小哲设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
D
O
D
C
B
A
【当堂检测】
2.如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小戴想估测这两根电线杆之间的距离,于是小戴从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小戴测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
解:(1)根据题意画出图形,如图所示.
【当堂检测】
(2)如果小戴一步大约60厘米,请你求A、B两根电线杆之间的距离.
解:由题可知∠BAC=∠EDC=90°,60cm=0.6m,
AC=20×0.6=12m,DC=20×0.6=12m,DE=100×0.6=60m,
∵点E、C、B在一条直线上,∴∠DCE=∠ACB.
∵∠BAC=∠EDC=90°,AC=DC,∠DCE=∠ACB,
∴△ABC≌△DEC,∴AB=DE.
∵DE=60m,∴AB=60m,
答:A、B两根电线杆之间的距离大约为60m.
四、课堂总结
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
方法:转化思想.
第四章 三角形
4.5 利用三角形全等测距离
1.能运用三角形全等测量距离,解决实际生活中的相关问题.
2.掌握三角形全等性质的应用.(重点)
一、学习目标
二、新课导入
回顾:
我们已经学过判定全等三角形的方法有哪些?
全等三角形的性质:
全等三角形对应边相等,对应角相等.
SSS
SAS
ASA
AAS
三、概念剖析
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离.由于没有任何测量工具,我八路军战士为
此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功.
利用三角形全等测距离
三、概念剖析
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
A
H
A'
H'
B
B'
?
三、概念剖析
理由:在△AHB与△A'H'B'中,
∠A=∠A'
AH=A'H'
∠H=∠H'
△AHB≌△A'H'B'(ASA)
BH=B'H'
A
A'
B
B'
H'
H
(全等三角形的对应边相等)
三、概念剖析
根据上述例子我们得出结论:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
例1.小强为了测量一栋高楼的高度AB,在旗杆CD与楼之间选定一点P.测得在P点观察旗杆顶C的视线PC与地面的夹角∠DPC=36°,测得在P点观察楼顶A的视线PA与地面的夹角∠APB=54°,量得P到楼底的距离PB与旗杆的高度相等,均为10米,量得旗杆与楼之间的距离DB=36米,如图,小强计算出了楼高,楼高AB是多少米?
分析:根据题意可得△CPD≌△PAB,进而利用AB=DP=DB-PB求出楼高.
典型例题
解:∵∠DPC=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵
∴△CPD≌△PAB(ASA),∴PD=AB,
∵DB=36,PB=10,∴AB=36-10=26(m),
答:楼高AB是26米.
∠CDP=∠PBA
DC=PB
∠DCP=∠BPA
典型例题
如何求未知线段?
途径:利用三角形全等
方法:转化思想
典型例题
归纳总结:
【当堂检测】
1.如图所示小哲设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
D
O
D
C
B
A
【当堂检测】
2.如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小戴想估测这两根电线杆之间的距离,于是小戴从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小戴测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
解:(1)根据题意画出图形,如图所示.
【当堂检测】
(2)如果小戴一步大约60厘米,请你求A、B两根电线杆之间的距离.
解:由题可知∠BAC=∠EDC=90°,60cm=0.6m,
AC=20×0.6=12m,DC=20×0.6=12m,DE=100×0.6=60m,
∵点E、C、B在一条直线上,∴∠DCE=∠ACB.
∵∠BAC=∠EDC=90°,AC=DC,∠DCE=∠ACB,
∴△ABC≌△DEC,∴AB=DE.
∵DE=60m,∴AB=60m,
答:A、B两根电线杆之间的距离大约为60m.
四、课堂总结
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
方法:转化思想.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
